TL;DR#
Minimum Bayes Risk (MBR) decoding offers superior translation quality but suffers from high computational cost, hindering its widespread use. Existing approximation methods either compromise quality or offer limited efficiency gains. This is a major bottleneck for researchers needing to use MBR decoding on larger datasets.
This research introduces a novel approach, Probabilistic Minimum Bayes Risk (PMBR), leveraging low-rank matrix completion algorithms to approximate MBR decoding. PMBR significantly reduces computational costs by 1/16, matching the translation quality of full MBR decoding, demonstrated empirically on machine translation tasks using COMET and MetricX metrics. This achievement opens new possibilities for efficiently employing the highly effective MBR decoding process in various applications.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel and efficient method for approximating Minimum Bayes Risk (MBR) decoding, a crucial task in machine translation and other natural language processing applications. The proposed method significantly reduces the computational cost of MBR decoding without compromising translation quality, opening avenues for broader application of this powerful decoding strategy. This addresses a critical limitation of MBR decoding and is highly relevant to researchers working on improving efficiency and accuracy in machine translation and related fields.
Visual Insights#

🔼 This figure illustrates the core idea of PMBR (Probabilistic Minimum Bayes Risk) decoding. It shows how PMBR uses matrix completion to efficiently approximate the full MBR decoding process. Instead of computing all pairwise utility scores between candidate hypotheses and pseudo-references (which is computationally expensive in vanilla MBR decoding), PMBR only computes scores for a random subset of pairs. Then, a matrix completion algorithm (ALS in this case) is used to fill in the missing entries, approximating the full utility matrix. The hypothesis with the highest average score across all (now approximated) pseudo-references is then selected as the final translation.
read the caption
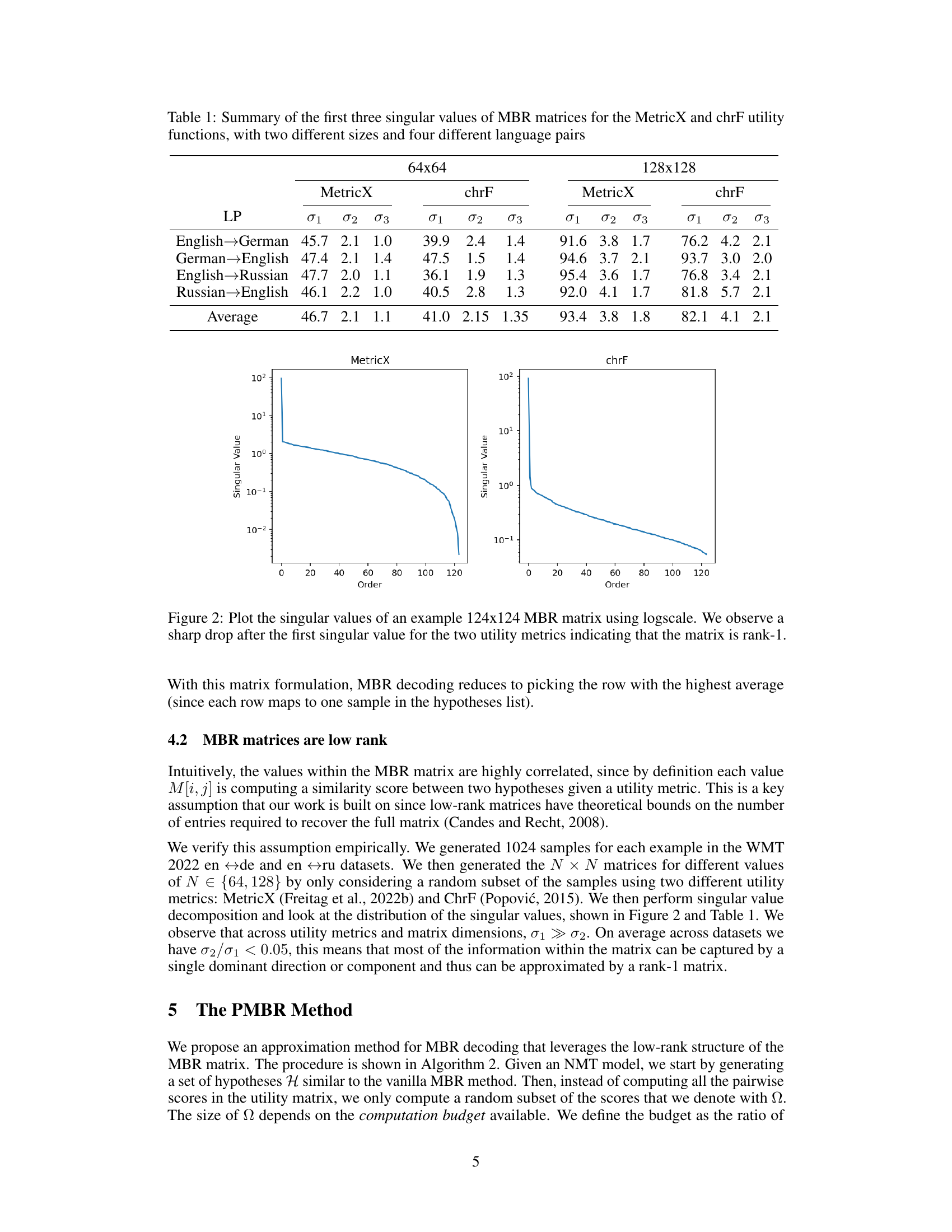
Figure 1: PMBR decoding only requires a subset of the utility computations to approximate the output of MBR decoding. The method approximates the unknown values by running a matrix completion algorithm which exploits the low-rank nature of the MBR matrix. Once the full matrix is recovered, the method behaves similar to the vanilla MBR decoding method where the hypothesis with the highest average score is selected.

🔼 This table presents a summary of the first three singular values of Minimum Bayes Risk (MBR) matrices. It shows the singular values (σ1, σ2, σ3) for two different matrix sizes (64x64 and 128x128) and four different language pairs (English-German, German-English, English-Russian, Russian-English). Two different utility functions, MetricX and chrF, are used. The data demonstrates that the MBR matrices are low-rank, with the first singular value significantly larger than the subsequent ones.
read the caption
Table 1: Summary of the first three singular values of MBR matrices for the MetricX and chrF utility functions, with two different sizes and four different language pairs
In-depth insights#
Low-Rank MBR#
The concept of “Low-Rank MBR” suggests a novel approach to Minimum Bayes Risk (MBR) decoding, a computationally expensive technique used in machine translation and other natural language processing tasks. The “low-rank” aspect likely refers to the structure of the utility matrix representing the scores of different translation hypotheses against pseudo-references. By demonstrating that this matrix is low-rank, the method can leverage matrix completion techniques to significantly reduce computational cost. This is achieved by only computing a subset of the entries and efficiently recovering the missing entries using algorithms like Alternating Least Squares (ALS). The significant reduction in computational complexity is a key advantage, allowing MBR decoding, known for its superior translation quality, to become more practical for large-scale applications. The effectiveness of this method likely hinges on the accuracy of the low-rank approximation and the choice of matrix completion algorithm. Further investigation is needed to explore the trade-off between accuracy and computational savings depending on the specific application and dataset.
ALS Matrix Completion#
The heading ‘ALS Matrix Completion’ suggests a section detailing the application of the Alternating Least Squares (ALS) algorithm for matrix completion within a research paper. ALS is a widely used iterative method to estimate missing values in a low-rank matrix by alternatively optimizing each factor matrix while keeping the other fixed. This is particularly relevant if the data exhibits a low-rank structure, implying that the observed relationships can be explained by a smaller number of latent factors. In the context of the paper, the low-rank matrix likely represents utility scores or other similarity measures between pairs of items. The choice of ALS might stem from its simplicity and scalability, making it suitable for large datasets. However, the summary should also discuss potential limitations, such as sensitivity to the initialization and convergence speed, and compare ALS with other matrix completion techniques if used in the paper. The section will likely present the algorithm’s implementation details, results of its application to the specific dataset, and possibly its impact on the overall performance of the proposed system. The effectiveness of ALS in recovering the missing entries directly impacts the accuracy and efficiency of the downstream task.
PMBR Decoding#
PMBR decoding, a probabilistic Minimum Bayes Risk (MBR) decoding method, offers a significant advancement in machine translation by efficiently approximating the computationally expensive MBR process. It leverages the observation that utility score matrices in MBR are inherently low-rank, meaning they can be accurately represented by a smaller set of underlying factors. By only calculating scores for a random subset of candidate-pseudo-reference pairs and then employing a matrix completion algorithm like Alternating Least Squares (ALS) to reconstruct the full matrix, PMBR significantly reduces the computational burden. The core strength lies in achieving near-identical translation quality to full MBR decoding while requiring far fewer utility metric computations (up to a 16x reduction was shown). This efficiency is especially crucial when working with computationally intensive neural utility metrics. Practical applicability is substantially enhanced because of the reduced cost, making PMBR a viable alternative to standard MBR for large-scale tasks.
Computational Savings#
The core idea behind achieving computational savings in Minimum Bayes Risk (MBR) decoding is to approximate the full utility matrix using matrix completion techniques. Instead of calculating the utility scores for all candidate-pseudo-reference pairs (a computationally expensive O(N²) operation), the proposed method, PMBR, strategically samples a subset of these pairs. This significantly reduces the computational burden. The low-rank property of the utility matrix, empirically demonstrated in the paper, is key to the success of this approximation. The Alternating Least Squares (ALS) algorithm is then employed to efficiently recover the missing entries of the matrix, providing a fast approximation of the full MBR scores. The paper highlights the trade-off between the computational savings achieved via reduced sampling and the quality of the approximation. Experimental results show significant gains, with the method achieving the same translation quality as full MBR decoding while requiring only a fraction (1/16) of the utility computations. This demonstrates the practicality and effectiveness of PMBR for large-scale machine translation tasks where computational efficiency is paramount. The low-rank matrix completion approach presents a promising avenue for optimizing MBR decoding in resource-constrained environments.
Future of MBR#
The future of Minimum Bayes Risk (MBR) decoding in machine translation and other natural language processing tasks hinges on addressing its computational cost. Approximation techniques, like the low-rank matrix completion method explored in the paper, are crucial. Further research into more efficient algorithms for matrix completion and exploration of alternative low-rank representations could drastically reduce the computational burden, making MBR more practical for large-scale applications. Additionally, developing more efficient utility metrics that accurately capture human judgment of translation quality will be essential. This might involve incorporating advances in neural scoring and incorporating human feedback more effectively into training. Furthermore, exploring the synergy between MBR and other decoding strategies like beam search could lead to hybrid approaches that leverage the strengths of both. Ultimately, the success of MBR will depend on a balance between computational efficiency and the accuracy of its approximation of human judgment, as well as its ability to adapt to evolving machine translation models.
More visual insights#
More on figures
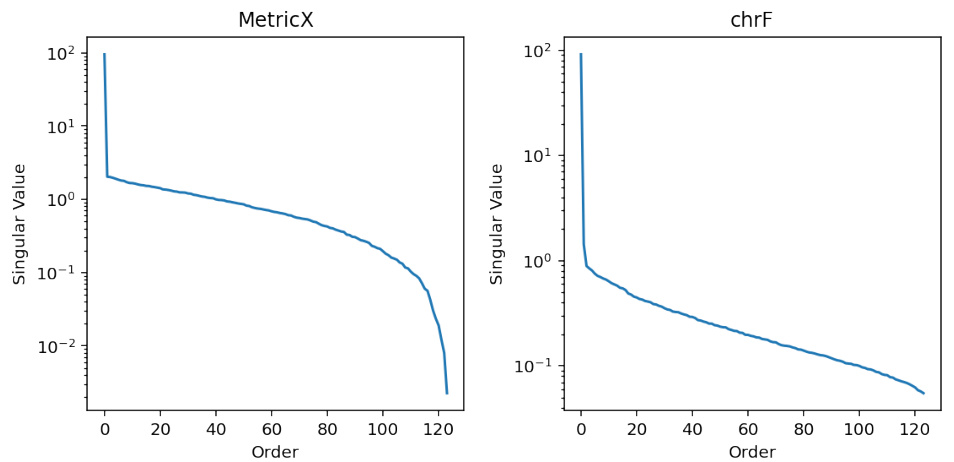
🔼 This figure shows the singular value decomposition of a 124x124 Minimum Bayes Risk (MBR) matrix, using two different utility metrics (MetricX and chrF). The plot demonstrates that the singular values sharply decrease after the first one, indicating that the matrix is effectively rank-1. This low-rank property is a key observation supporting the paper’s proposed approximation method. Because the matrix is nearly rank-1, MBR decoding simplifies to finding the row with the highest average value.
read the caption
Figure 2: Plot the singular values of an example 124x124 MBR matrix using logscale. We observe a sharp drop after the first singular value for the two utility metrics indicating that the matrix is rank-1. With this matrix formulation, MBR decoding reduces to picking the row with the highest average (since each row maps to one sample in the hypotheses list).
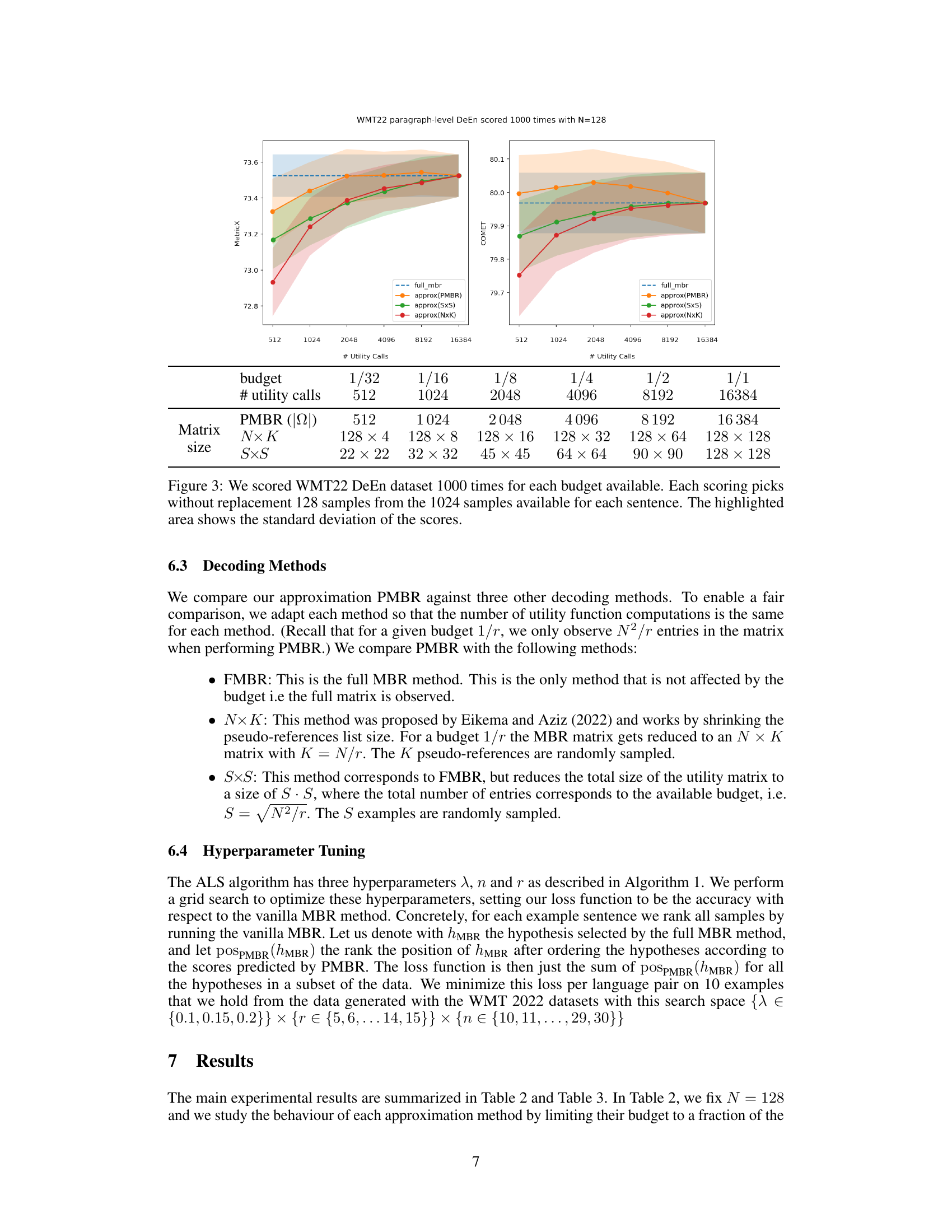
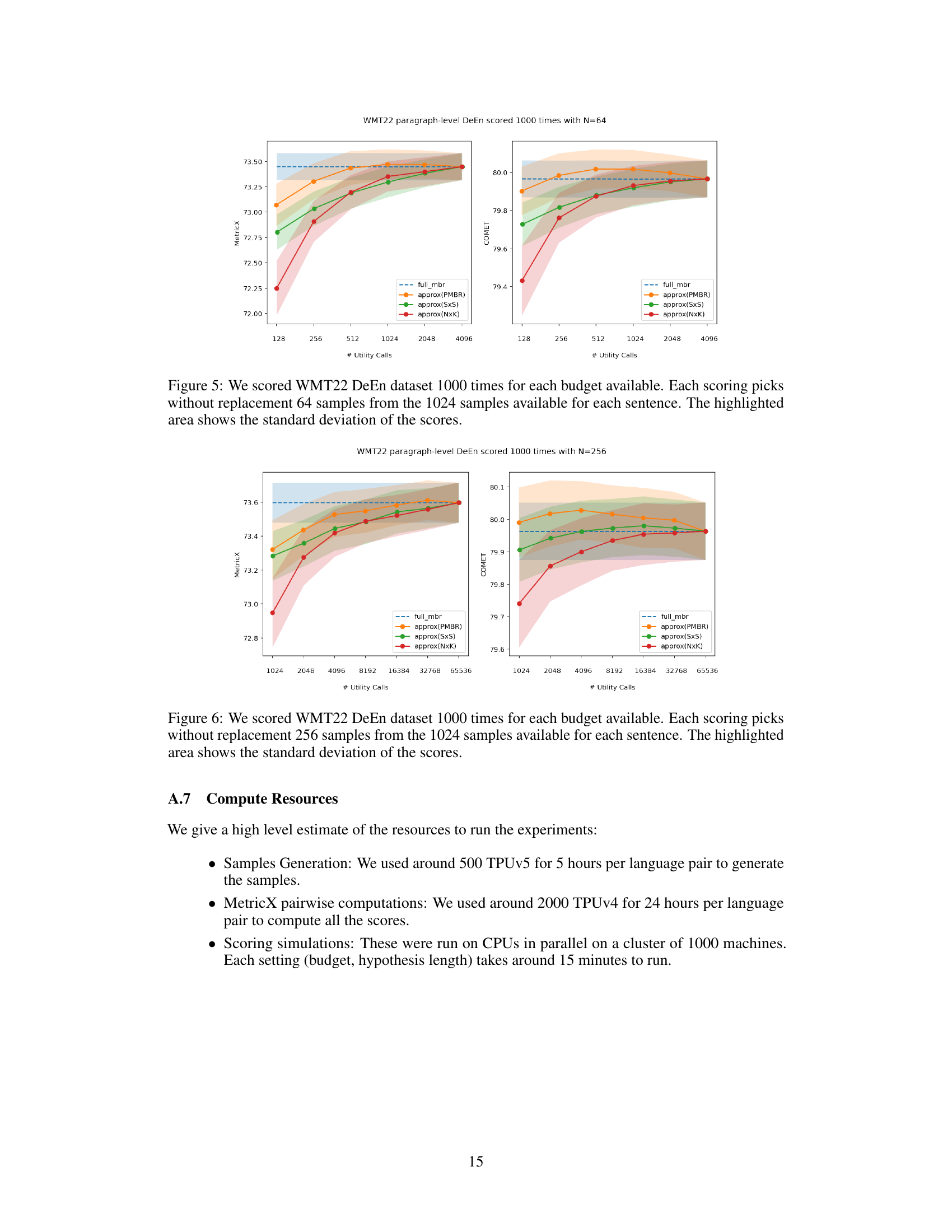
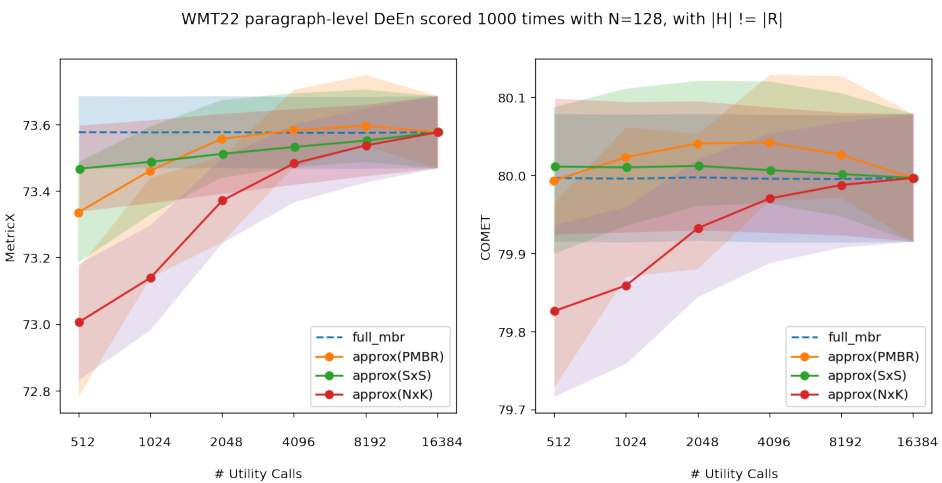
🔼 This figure shows the performance of different MBR decoding approximation methods (PMBR, NxK, SxS) compared to the full MBR method. The x-axis represents the number of utility calls (computational budget), and the y-axis shows the quality scores (MetricX and COMET). The shaded areas represent the standard deviations of the scores across multiple runs. The plot demonstrates that PMBR achieves similar quality to the full MBR method while significantly reducing the number of computations.
read the caption
Figure 3: We scored WMT22 DeEn dataset 1000 times for each budget available. Each scoring picks without replacement 128 samples from the 1024 samples available for each sentence. The highlighted area shows the standard deviation of the scores.
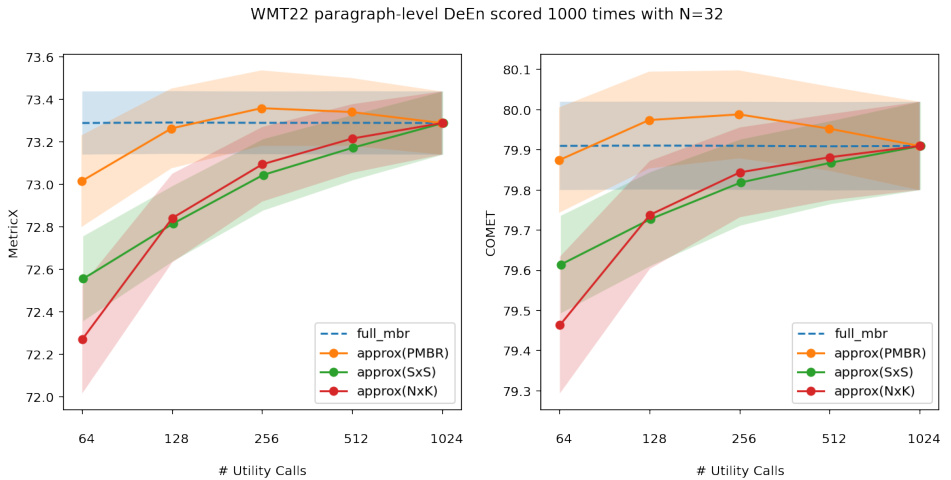
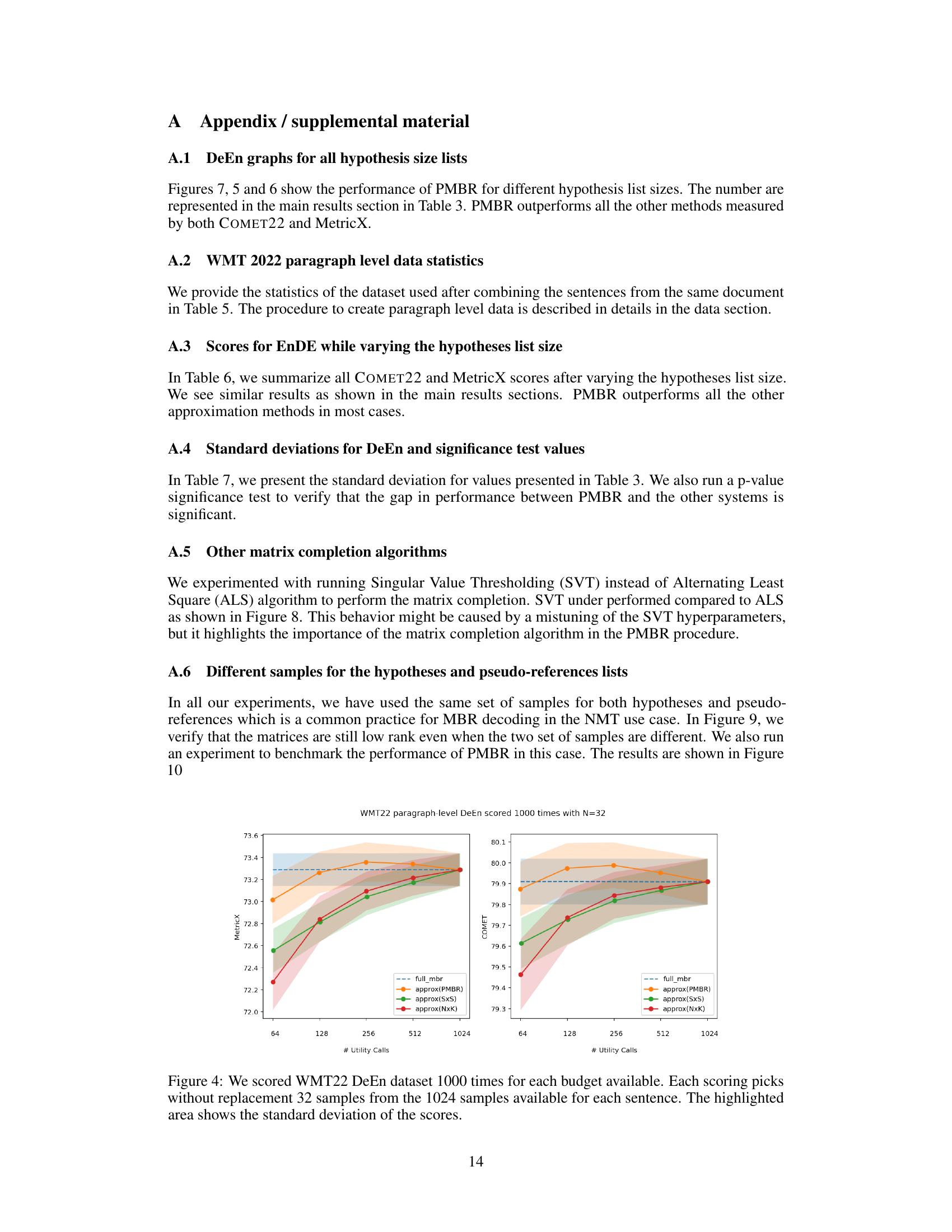
🔼 This figure displays the results of scoring the WMT22 DeEn dataset 1000 times for various budget levels, using 128 samples per sentence. The x-axis shows the number of utility calls (computations), representing different budget levels. The y-axis shows both the MetricX and COMET scores, representing translation quality. The lines represent different decoding methods: full MBR (the most accurate but computationally expensive), and three approximation methods (PMBR, SxS, NxK). The shaded area around each line indicates the standard deviation of the scores across the 1000 runs, providing a measure of the variability in the results for each method.
read the caption
Figure 3: We scored WMT22 DeEn dataset 1000 times for each budget available. Each scoring picks without replacement 128 samples from the 1024 samples available for each sentence. The highlighted area shows the standard deviation of the scores.

🔼 This figure displays the results of scoring the WMT22 DeEn dataset 1000 times for various budget levels. Each scoring instance randomly selects 128 samples from the available 1024 samples for each sentence. The shaded regions represent the standard deviation of the scores across these multiple runs. The figure compares the performance of four decoding methods: full MBR, approximate PMBR, approximate SxS, and approximate NxK, demonstrating how their MetricX and COMET scores vary with different computational budgets.
read the caption
Figure 3: We scored WMT22 DeEn dataset 1000 times for each budget available. Each scoring picks without replacement 128 samples from the 1024 samples available for each sentence. The highlighted area shows the standard deviation of the scores.

🔼 This figure shows the performance of four different decoding methods (full MBR, PMBR, NxK, and SxS) on the WMT22 German-English translation task, using both MetricX and COMET metrics. The x-axis represents the number of utility calls (a measure of computational cost), while the y-axis represents the quality scores (MetricX and COMET). The shaded areas indicate the standard deviation across 1000 runs for each method and budget, demonstrating the consistency and reliability of the results. The figure highlights that PMBR closely matches the performance of full MBR while significantly reducing the number of utility calls, showcasing its efficiency.
read the caption
Figure 3: We scored WMT22 DeEn dataset 1000 times for each budget available. Each scoring picks without replacement 128 samples from the 1024 samples available for each sentence. The highlighted area shows the standard deviation of the scores.
🔼 This figure compares the performance of several Minimum Bayes Risk (MBR) decoding approximation methods against the full MBR method on the WMT22 English-German translation task. The x-axis represents the number of utility calls (a measure of computational cost), and the y-axis shows the resulting MetricX and COMET scores, which measure translation quality. Different colors represent different approximation methods (PMBR, NxK, and SxS). The shaded area illustrates the standard deviation of the scores across multiple runs for each method and budget.
read the caption
Figure 3: We scored WMT22 DeEn dataset 1000 times for each budget available. Each scoring picks without replacement 128 samples from the 1024 samples available for each sentence. The highlighted area shows the standard deviation of the scores.
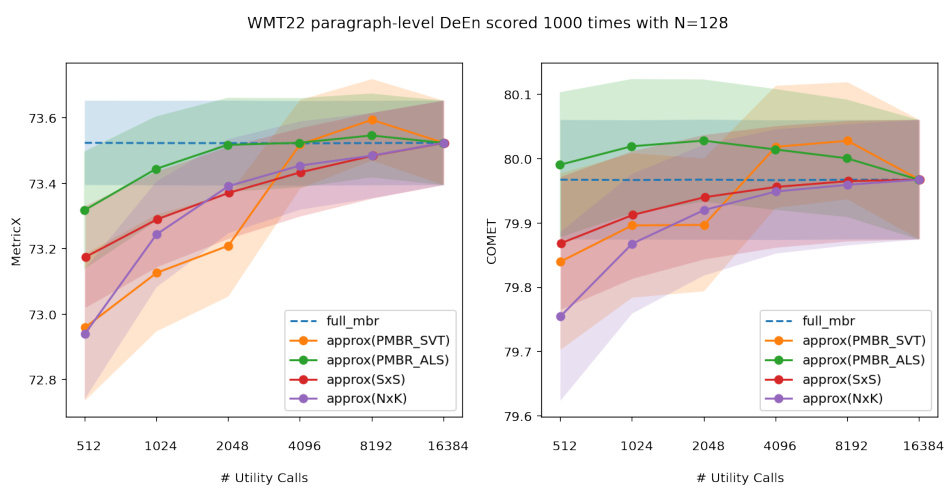
🔼 This figure displays the results of scoring the WMT22 DeEn dataset 1000 times using different budget levels for five different decoding methods: full MBR, PMBR with SVT, PMBR with ALS, NxK, and SxS. The x-axis shows the number of utility calls made, which is directly related to the computational cost. The y-axis shows the achieved scores, broken into two subplots: one for MetricX and another for COMET. The shaded regions around the lines represent the standard deviation of the scores across the 1000 runs for each method and budget, illustrating the variability of the results. The dashed horizontal line represents the score achieved by the full MBR method, serving as a baseline for comparison. The plot helps to visualize the trade-off between computational cost (number of utility calls) and the quality of the approximation (MetricX and COMET scores) for different MBR approximation techniques.
read the caption
Figure 3: We scored WMT22 DeEn dataset 1000 times for each budget available. Each scoring picks without replacement 128 samples from the 1024 samples available for each sentence. The highlighted area shows the standard deviation of the scores.
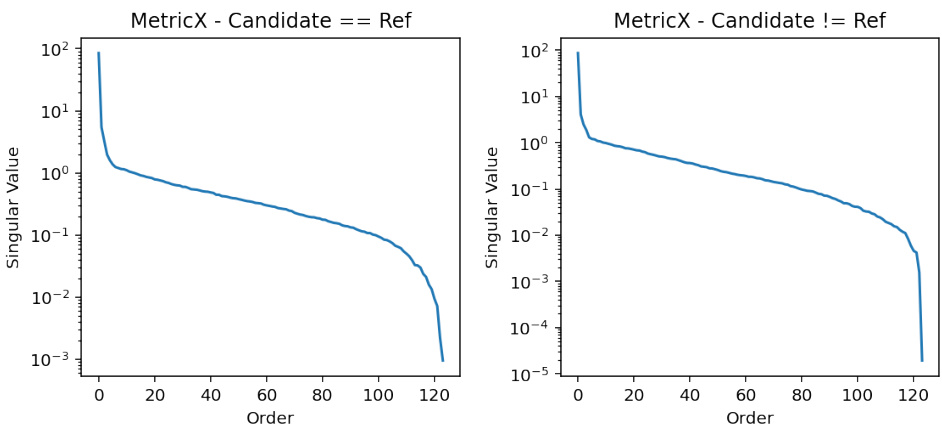
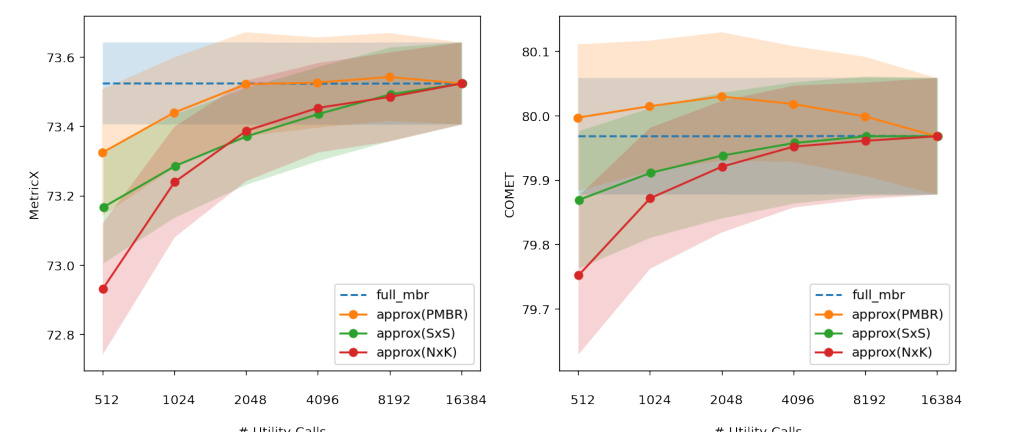
🔼 This figure empirically demonstrates the low-rank nature of the MBR matrix, regardless of whether the same set of samples is used for hypotheses and pseudo-references. The plots display the singular values for two scenarios. The left shows the case where the samples for hypotheses and pseudo-references are the same, while the right depicts the case with different sample sets. Both scenarios exhibit a sharp decline in singular values after the first, supporting the low-rank assumption central to the proposed PMBR method.
read the caption
Figure 9: Plot the singular values of an example 124x124 MBR matrix using logscale. The plot on the left shows the case where both the samples for hypotheses and pseudo-references lists, while the right shows the case when they are different. Both plots follow a similar pattern.
🔼 This figure displays the performance of four different decoding methods (full MBR, PMBR, NxK, and SxS) on the WMT22 DeEn dataset. The x-axis represents the number of utility calls, which reflects the computational cost. The y-axis shows the scores obtained using MetricX and COMET22. Each method is tested 1000 times with 128 samples randomly selected from the available 1024 samples for each sentence. The shaded area represents the standard deviation, illustrating the variability of the results. The plot showcases how the approximation methods perform compared to the full MBR method across different computational budgets.
read the caption
Figure 3: We scored WMT22 DeEn dataset 1000 times for each budget available. Each scoring picks without replacement 128 samples from the 1024 samples available for each sentence. The highlighted area shows the standard deviation of the scores.
More on tables
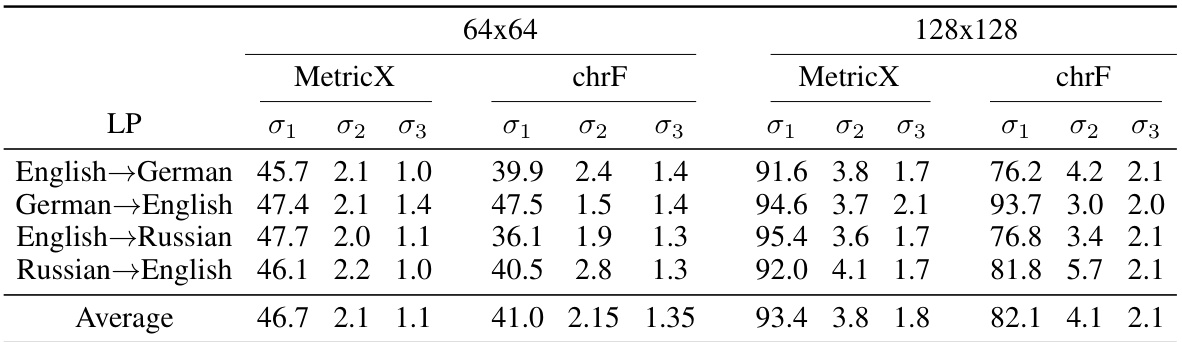
🔼 This table presents the first three singular values (σ1, σ2, σ3) of Minimum Bayes Risk (MBR) matrices calculated using two different utility functions (MetricX and chrF) and two different matrix sizes (64x64 and 128x128). The results are shown for four different language pairs: English-German, German-English, English-Russian, and Russian-English. The singular values help illustrate the low-rank nature of the MBR matrices, supporting the use of low-rank matrix completion for efficient MBR decoding.
read the caption
Table 1: Summary of the first three singular values of MBR matrices for the MetricX and chrF utility functions, with two different sizes and four different language pairs

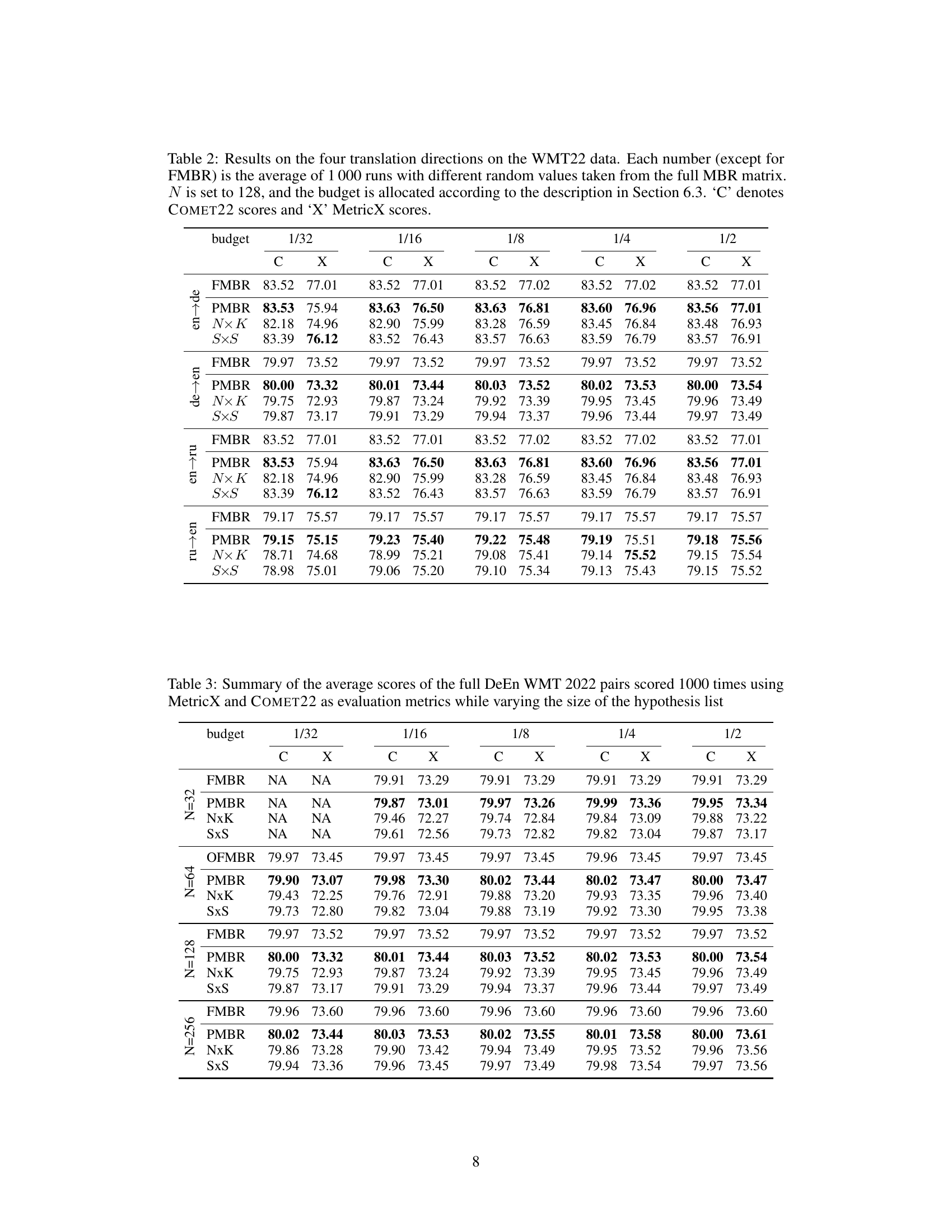
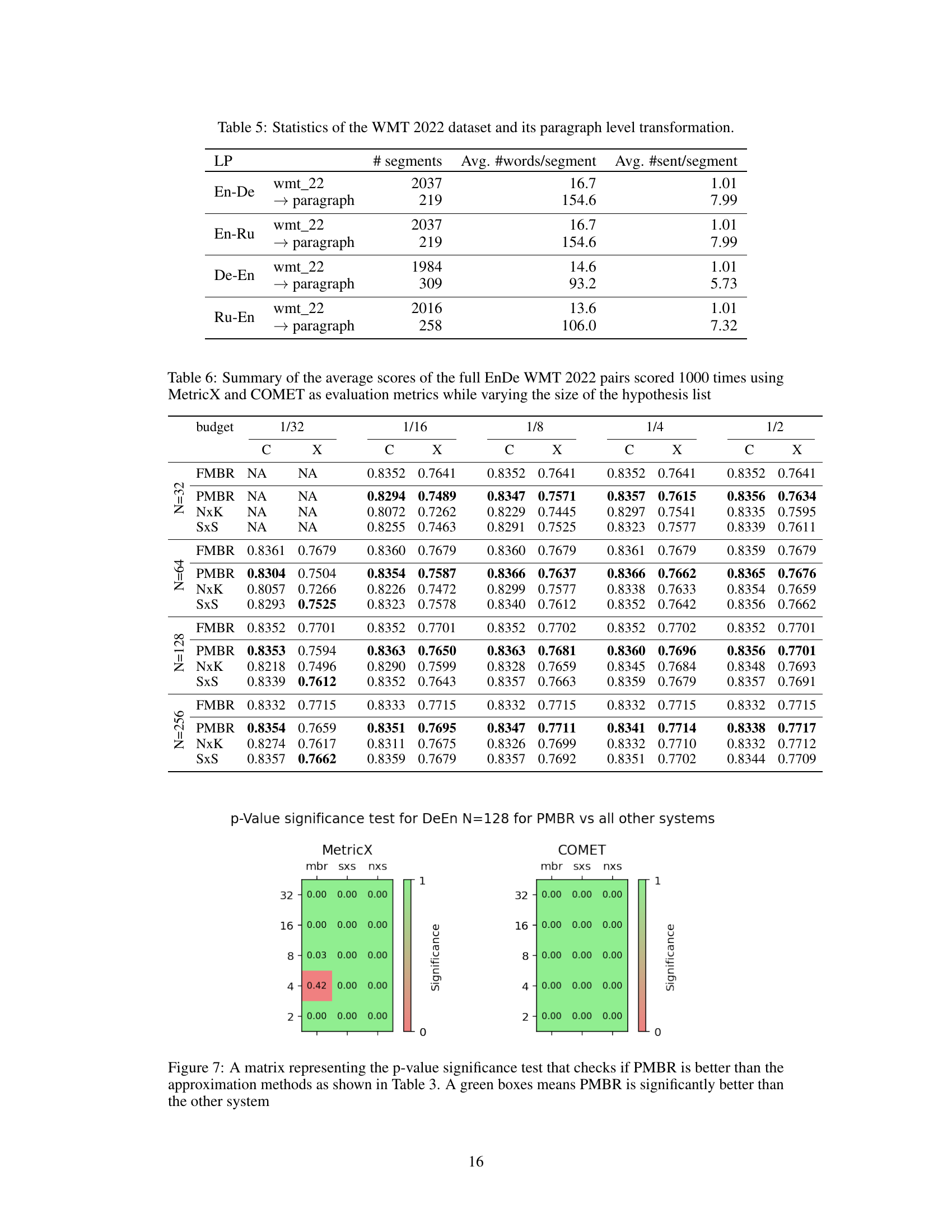
🔼 This table presents the results of the four translation directions on the WMT22 dataset. Each score (except for the full MBR method, FMBR) represents the average of 1000 runs with different random samples from the full MBR matrix. The experiment uses a candidate list size (N) of 128 and varying budgets (1/32, 1/16, 1/8, 1/4, 1/2) allocated as described in Section 6.3 of the paper. The scores are reported for both COMET22 (C) and MetricX (X) metrics.
read the caption
Table 2: Results on the four translation directions on the WMT22 data. Each number (except for FMBR) is the average of 1000 runs with different random values taken from the full MBR matrix. N is set to 128, and the budget is allocated according to the description in Section 6.3. 'C' denotes COMET22 scores and 'X' MetricX scores.

🔼 This table presents the results of the four translation directions on the WMT22 dataset. Each cell shows the average score (COMET22 and MetricX) over 1000 runs, each with different random samples of the full MBR matrix. The results are for different budget levels (1/32 to 1/1), affecting the number of utility calls and the size of the matrix processed. The table compares the performance of the proposed PMBR method against full MBR (FMBR), NxK, and SxS methods. The number of candidates (N) is fixed at 128.
read the caption
Table 2: Results on the four translation directions on the WMT22 data. Each number (except for FMBR) is the average of 1000 runs with different random values taken from the full MBR matrix. N is set to 128, and the budget is allocated according to the description in Section 6.3. ‘C’ denotes COMET22 scores and ‘X’ MetricX scores.

🔼 This table presents the results of the four translation directions on the WMT22 dataset. The table shows the performance of different decoding methods (Full MBR, PMBR, N×K, and S×S) with varying computational budgets (1/32, 1/16, 1/8, 1/4, 1/2). Each score (except for the full MBR method) is an average of 1000 runs with different random samples from the full MBR matrix. The results are reported using two metrics: COMET22 (C) and MetricX (X).
read the caption
Table 2: Results on the four translation directions on the WMT22 data. Each number (except for FMBR) is the average of 1000 runs with different random values taken from the full MBR matrix. N is set to 128, and the budget is allocated according to the description in Section 6.3. ‘C’ denotes COMET22 scores and ‘X’ MetricX scores.

🔼 This table presents the results of the four translation directions on the WMT22 dataset. Each score (except for the full MBR method, FMBR) is an average across 1000 trials, each using a different random sample from the full MBR matrix. The experiment uses a fixed hypothesis list size (N=128), and varying computational budgets (specified as a fraction of the full computation cost). The table shows both COMET22 and MetricX scores for each condition.
read the caption
Table 2: Results on the four translation directions on the WMT22 data. Each number (except for FMBR) is the average of 1000 runs with different random values taken from the full MBR matrix. N is set to 128, and the budget is allocated according to the description in Section 6.3. 'C' denotes COMET22 scores and 'X' MetricX scores.
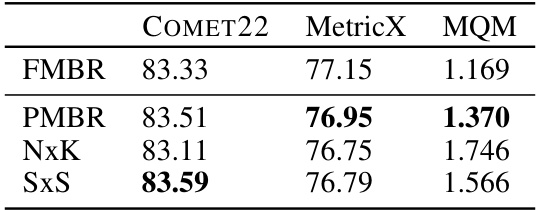
🔼 This table summarizes the average scores for the English-to-German translation task on the WMT22 dataset, using three different metrics: COMET22, MetricX, and MQM. The results are based on 1000 runs with a hypothesis list size of N=256 and a budget of r=1/16. The MQM scores are limited to the 65 examples where there was disagreement among all systems to reduce bias, focusing on a comparison of the more uncertain cases.
read the caption
Table 4: Summary of the average scores of the full EnDe WMT 2022 with N=256 and r=1/16 pairs scored 1000 times using MetricX and COMET22. The MQM scores are limited to 65 examples where all systems disagreed.
🔼 This table presents a summary of the first three singular values of Minimum Bayes Risk (MBR) matrices. These matrices represent similarity scores between candidate hypotheses and pseudo-references in machine translation tasks, using two different utility functions (MetricX and chrF). The data is broken down by four different language pairs (English-German, German-English, English-Russian, Russian-English) and two matrix sizes (64x64 and 128x128). The singular values reveal the low-rank nature of the matrices, which is a key finding supporting the use of low-rank matrix completion algorithms for approximating MBR decoding.
read the caption
Table 1: Summary of the first three singular values of MBR matrices for the MetricX and chrF utility functions, with two different sizes and four different language pairs
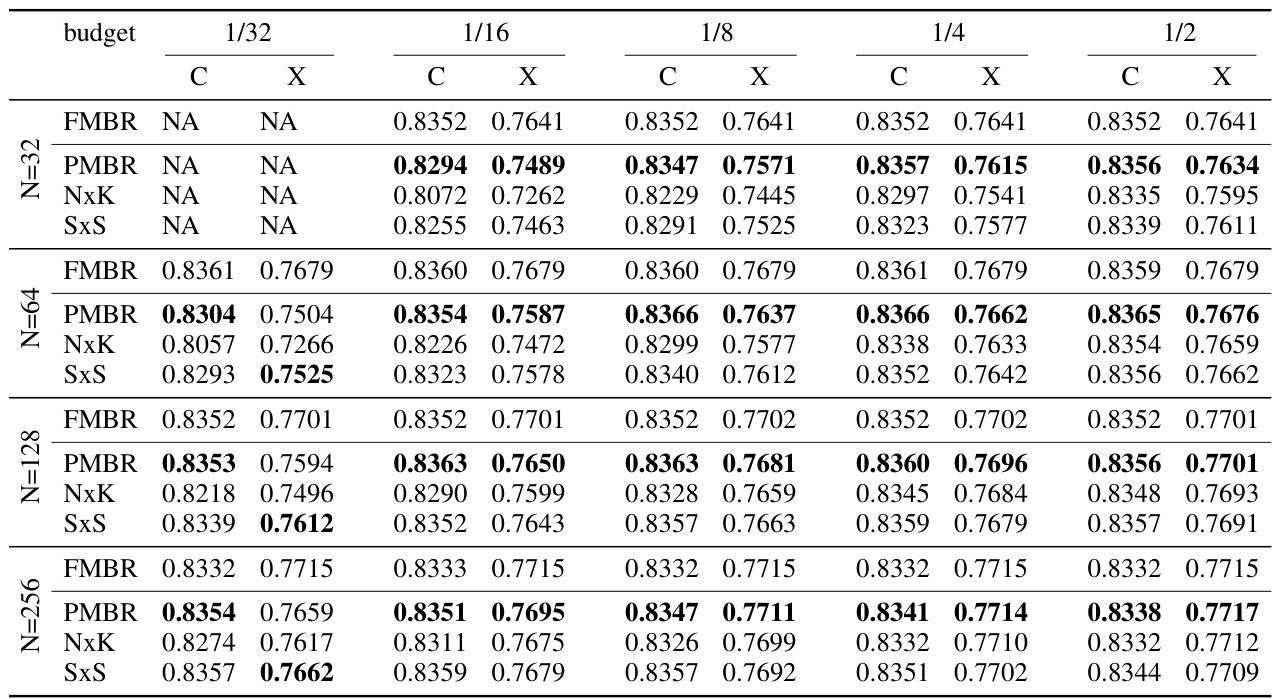
🔼 This table presents the results of the four translation directions on the WMT22 dataset. It compares the performance of the full MBR method (FMBR) against three approximation methods (PMBR, NxK, SxS) under various budget constraints. Each non-FMBR result is an average of 1000 runs, each with a different random sample of scores from the full matrix. The table shows COMET22 and MetricX scores for each method under each budget.
read the caption
Table 2: Results on the four translation directions on the WMT22 data. Each number (except for FMBR) is the average of 1000 runs with different random values taken from the full MBR matrix. N is set to 128, and the budget is allocated according to the description in Section 6.3. ‘C’ denotes COMET22 scores and ‘X’ MetricX scores.
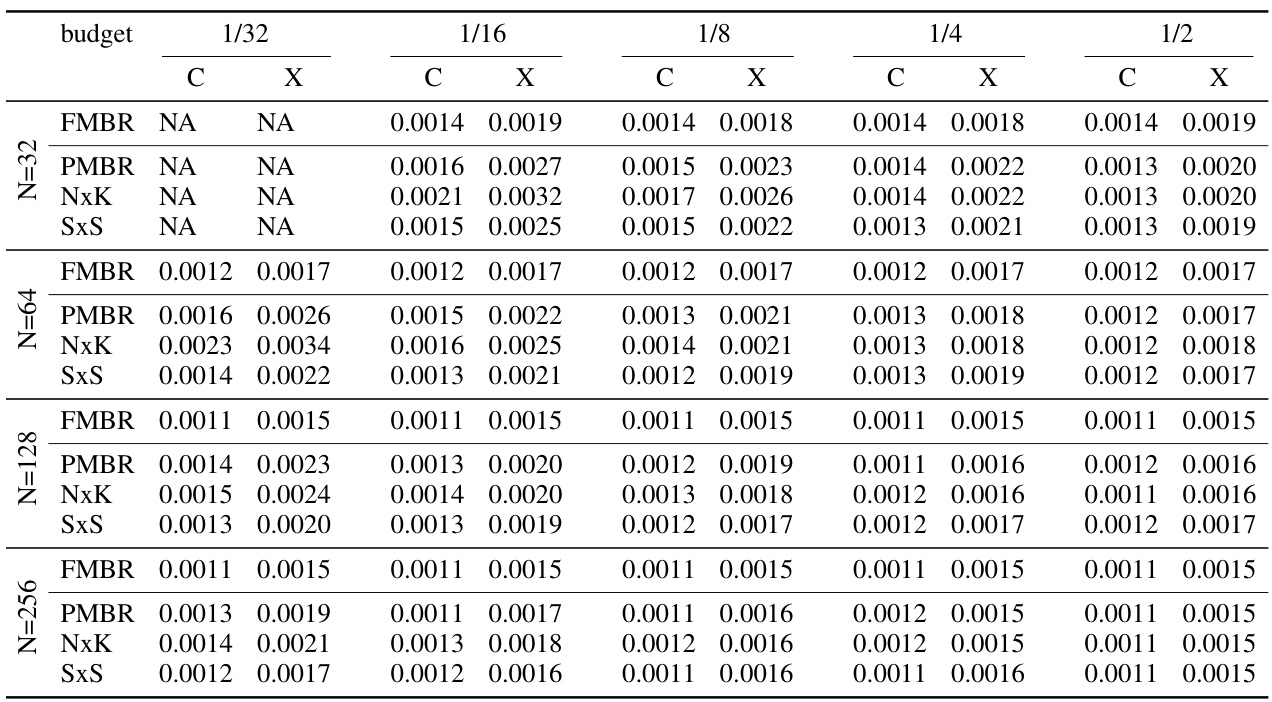
🔼 This table presents the standard deviations of the COMET and MetricX scores obtained from 1000 runs of the experiments detailed in Table 3. It shows the standard deviation for different hypothesis list sizes (N=32, 64, 128, 256) and budget levels (1/32, 1/16, 1/8, 1/4, 1/2), providing insights into the variability of the results.
read the caption
Table 7: Summary of the standard deviations of the full DeEn WMT 2022 pairs scored 1000 times using MetricX and COMET22 as evaluation metrics while varying the size of the hypothesis list as shown in Table 3
Full paper#