Visual Prompt Tuning in Null Space for Continual Learning

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in continual learning, especially those working with visual prompt tuning. It provides a novel theoretical framework and practical solution to mitigate catastrophic forgetting, a major challenge in the field. The proposed method achieves superior performance on benchmark datasets and opens up avenues for exploring orthogonal projection techniques in more complex architectures. This work will significantly advance the development of more robust and efficient continual learning models.

Visual Insights

#

🔼 This figure illustrates the forward propagation process within a single layer of a Vision Transformer (ViT) network, specifically focusing on how visual prompts are incorporated. The process is broken down into several stages: Layer Normalization (LN) of both the input image tokens and the prompts, the multi-head self-attention mechanism (including the Affinity and Aggregation stages), and finally, another Layer Normalization and Multi-Layer Perceptron (MLP). The figure highlights that only the image tokens are used in the subsequent calculations, while the prompt’s contribution to the final output is represented as a ‘red cross’ symbol, which means they can be discarded during fine-tuning of this layer.

read the caption

Figure 1: Illustration of the forward propagation in a ViT layer. Residual connections are omitted. The red crosses indicate the rows of attention map or the output prompts can be neglected.

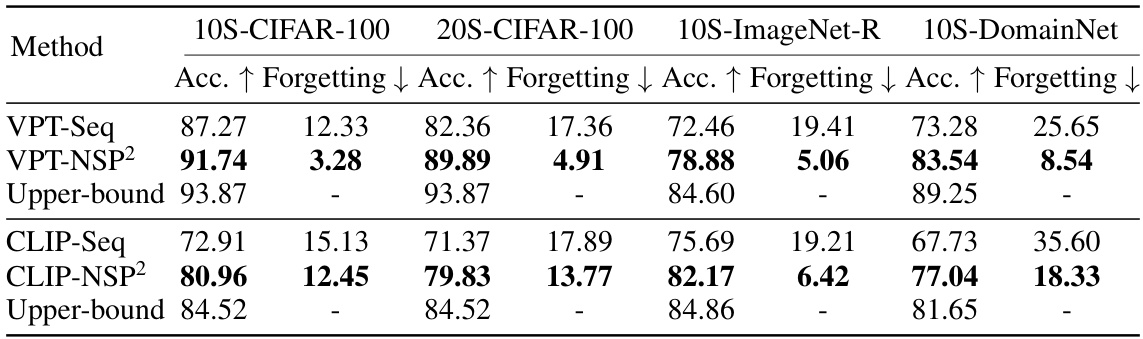
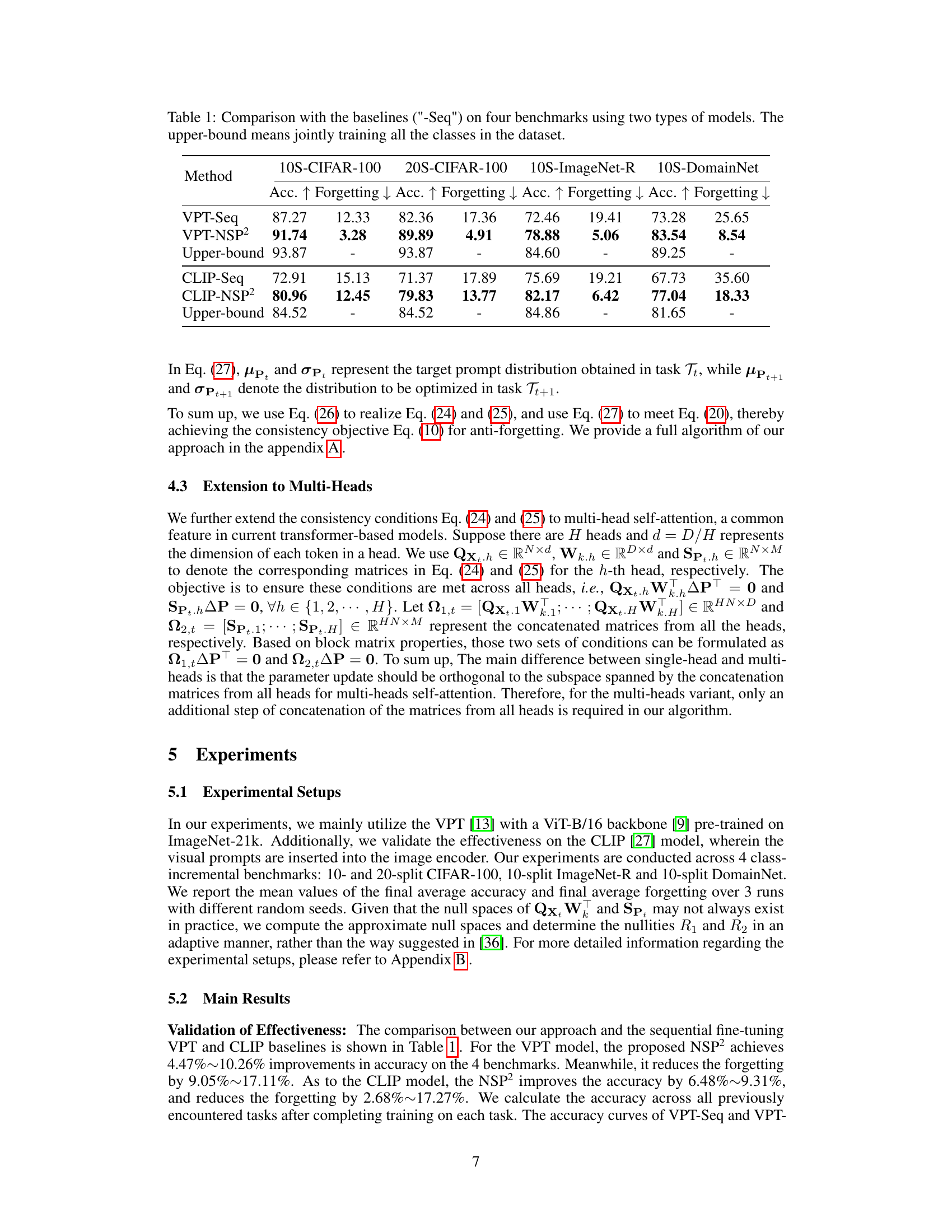
🔼 This table compares the performance of the proposed method, VPT-NSP2, against two baseline methods, VPT-Seq and CLIP-Seq, across four continual learning benchmarks. It shows the accuracy and forgetting rate for each method and benchmark. VPT-NSP2 consistently outperforms the baseline methods, demonstrating its effectiveness in mitigating catastrophic forgetting. The ‘Upper-bound’ row represents the best achievable performance if all classes were trained jointly.

read the caption

Table 1: Comparison with the baselines ('-Seq') on four benchmarks using two types of models. The upper-bound means jointly training all the classes in the dataset.

In-depth insights

#

Null-Space VPT

#

The concept of “Null-Space VPT” suggests a novel approach to visual prompt tuning (VPT) in continual learning. It leverages the null space of previously learned task representations to update prompts for new tasks, aiming to mitigate catastrophic forgetting. This orthogonal projection prevents interference with existing knowledge, a major challenge in continual learning. The method’s theoretical foundation likely involves deriving conditions ensuring consistency across tasks by updating prompts only within the null space. Practical implementation might involve techniques to approximate the null space, potentially using singular value decomposition or similar dimensionality reduction methods. The effectiveness hinges on the ability to precisely characterize and project into the null space of the high-dimensional embedding space used by vision transformers, addressing the non-linearity inherent in self-attention mechanisms. Experimental evaluation would focus on demonstrating improved performance and reduced forgetting compared to traditional VPT methods on standard continual learning benchmarks.

Consistency Conditions

#

The concept of “Consistency Conditions” in the context of continual learning and visual prompt tuning is crucial for preventing catastrophic forgetting. The core idea revolves around ensuring that updates to visual prompts do not negatively impact previously learned tasks. This necessitates deriving conditions under which the model’s output remains consistent when new prompts are introduced. The challenge lies in the complexity of the Vision Transformer (ViT) architecture, specifically its high-order and non-linear self-attention mechanism and the LayerNorm operation. Therefore, the consistency conditions aim to mathematically define the permissible directions for prompt updates such that these operations do not disrupt the previously learned feature representations. Satisfying these conditions effectively guarantees that newly learned tasks do not overwrite or interfere with previously acquired knowledge. The process of deriving such conditions involves a deep analysis of the forward propagation within the ViT layer, leading to a set of constraints on how prompts should be updated to ensure the consistency of the model’s output across different tasks. This analysis likely involves examining the interaction between prompts and input image tokens, the effect of LayerNorm and self-attention, and ultimately, deriving a set of mathematical conditions to uphold consistency.

NSP2 Algorithm

#

The NSP2 algorithm, a core contribution of this research paper, presents a novel approach to orthogonal projection within the context of visual prompt tuning for continual learning. It directly tackles the challenges posed by the non-linearity of the self-attention mechanism and the distribution drift introduced by LayerNorm in transformers. The algorithm’s strength lies in its theoretical grounding, deriving two consistency conditions to ensure that updating prompts for a new task doesn’t negatively impact previously learned tasks. A key innovation is the null-space-based approximation solution employed to practically implement the theoretically derived orthogonal projection. This solution effectively circumvents the complexities of directly applying orthogonal projection to the high-dimensional, non-linear transformations within the transformer architecture. The algorithm also incorporates a loss function that penalizes prompt distribution drift across tasks, further enhancing its stability and preventing catastrophic forgetting. By cleverly combining theoretical analysis with a practical approximation method, NSP2 offers a robust and effective solution for continual learning in vision transformer models. This approach is validated through extensive experiments, demonstrating significant performance improvements compared to state-of-the-art methods on several benchmark datasets.

Multi-Head Extension

#

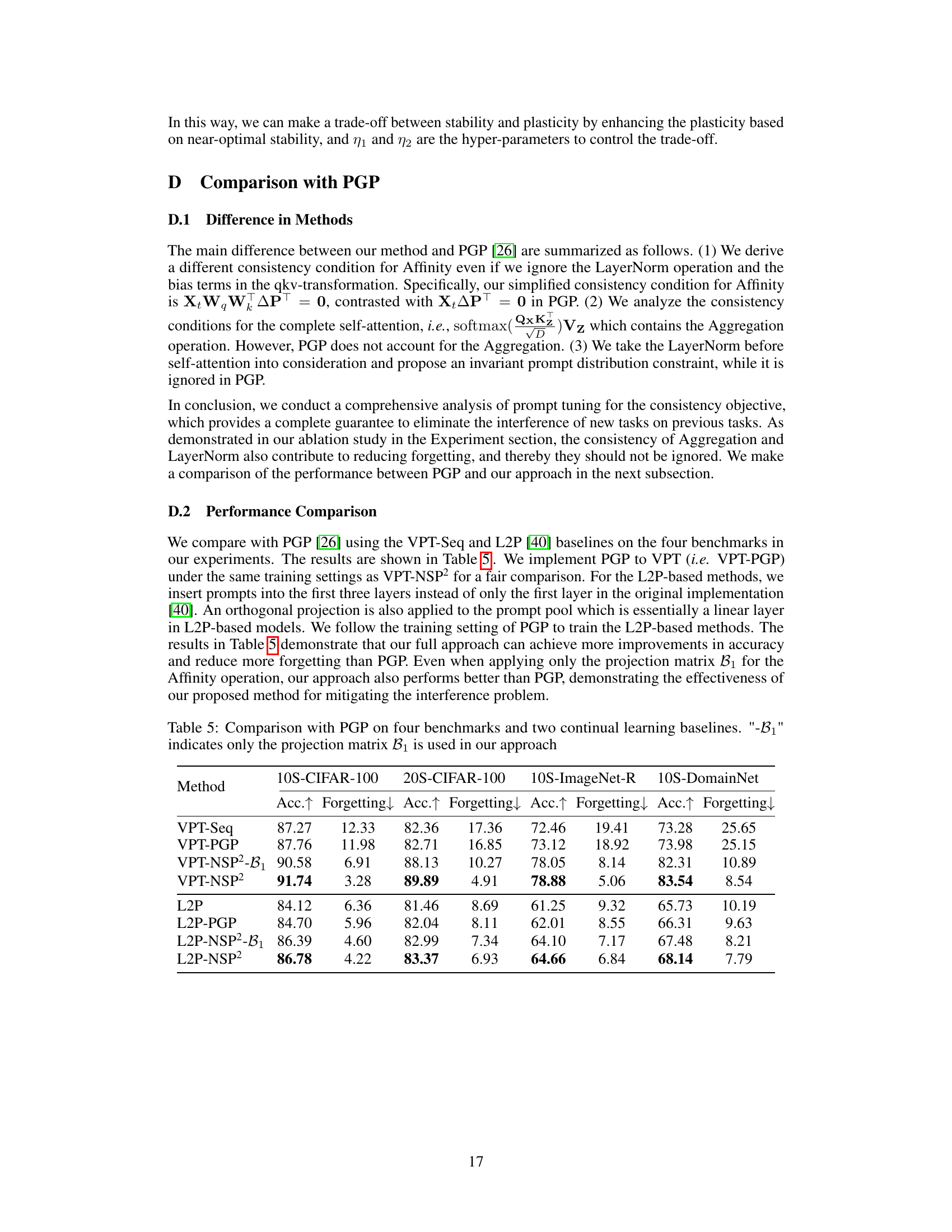
The multi-head extension in this research paper is a crucial aspect that addresses the scalability and applicability of the proposed prompt gradient orthogonal projection method to real-world scenarios. Standard transformer models utilize multi-head self-attention mechanisms, enhancing model capacity and expressiveness. The extension ensures that the theoretical guarantees for eliminating interference, derived for single-headed attention, also hold in the more complex multi-head setting. This is achieved by carefully extending the consistency conditions to encompass all attention heads, demonstrating the algorithm’s robustness. The extension likely involves concatenating matrices from all heads and then applying the orthogonal projection. This approach ensures that the prompt updates remain orthogonal to the combined subspace spanned by all heads’ features from previous tasks, effectively mitigating catastrophic forgetting across all heads. The successful extension significantly broadens the applicability of this technique, making it a practical solution for a wider range of visual prompt tuning tasks in continual learning settings.

Stability-Plasticity

#

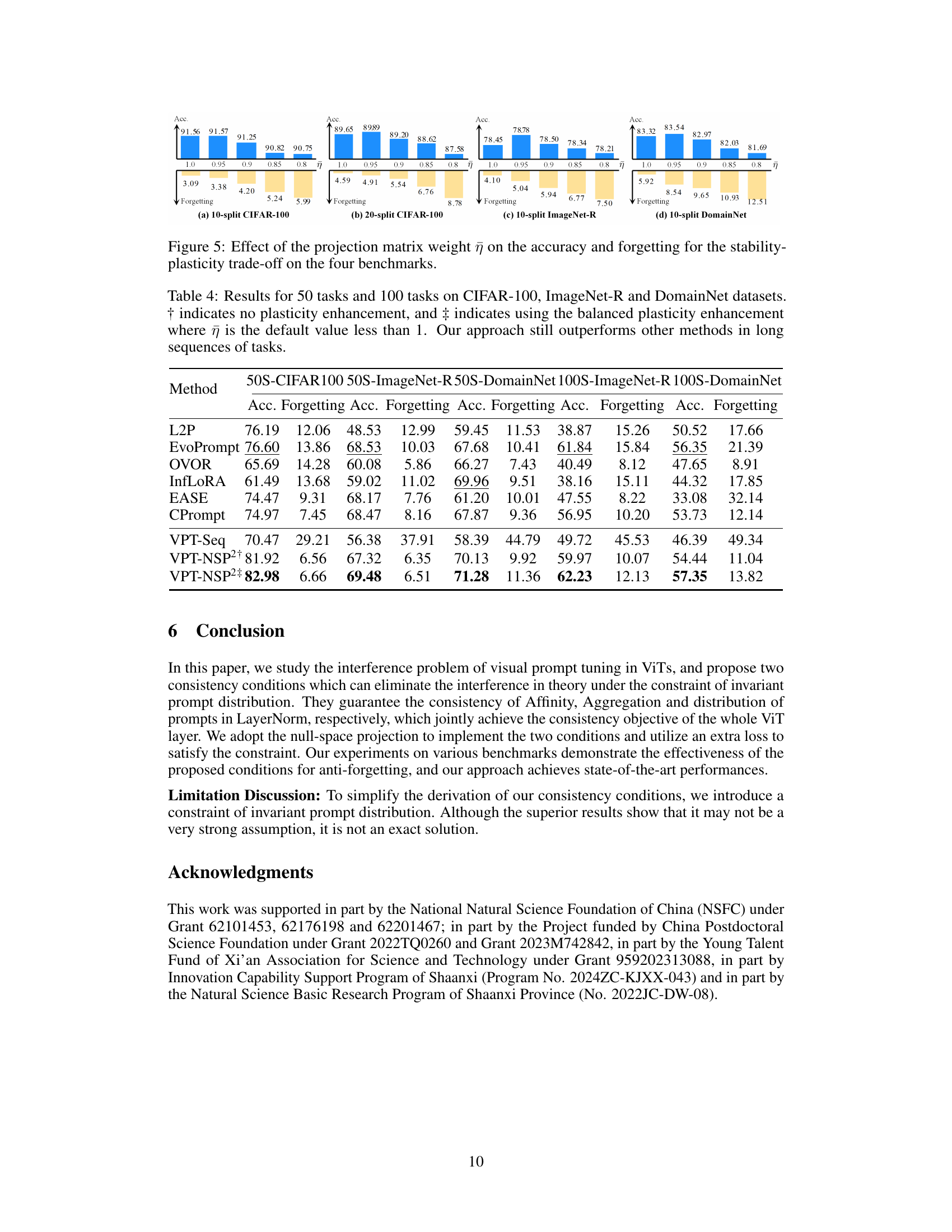
The concept of ‘Stability-Plasticity’ in continual learning is crucial. It highlights the inherent trade-off between a model’s ability to retain previously learned knowledge (stability) and its capacity to adapt to new information (plasticity). Finding the optimal balance is key to successful continual learning, as excessive stability leads to catastrophic forgetting, while excessive plasticity compromises the retention of past experiences. Effective continual learning algorithms must carefully manage this trade-off, often employing techniques like regularization, parameter isolation, or memory mechanisms to achieve a desired balance between stability and plasticity. Strategies for controlling this balance often involve hyperparameters or architectural choices that influence the weighting between preserving old information and acquiring new information. The success of any continual learning method significantly depends on its ability to navigate the stability-plasticity dilemma effectively.

More visual insights

#

More on figures

🔼 This figure shows the task-by-task accuracy curves for both the sequential fine-tuning baseline (VPT-Seq) and the proposed Null-Space Projection for Prompts (VPT-NSP2) method. The plots illustrate the performance on two benchmark datasets: 10-split CIFAR-100 and 10-split ImageNet-R. The x-axis represents the task number, while the y-axis shows the accuracy. This visualization demonstrates the effectiveness of VPT-NSP2 in mitigating catastrophic forgetting, as its accuracy remains consistently higher across tasks compared to the VPT-Seq baseline.

read the caption

Figure 2: Task-by-task accuracy changing curves of VPT-Seq and VPT-NSP2 on two benchmarks.

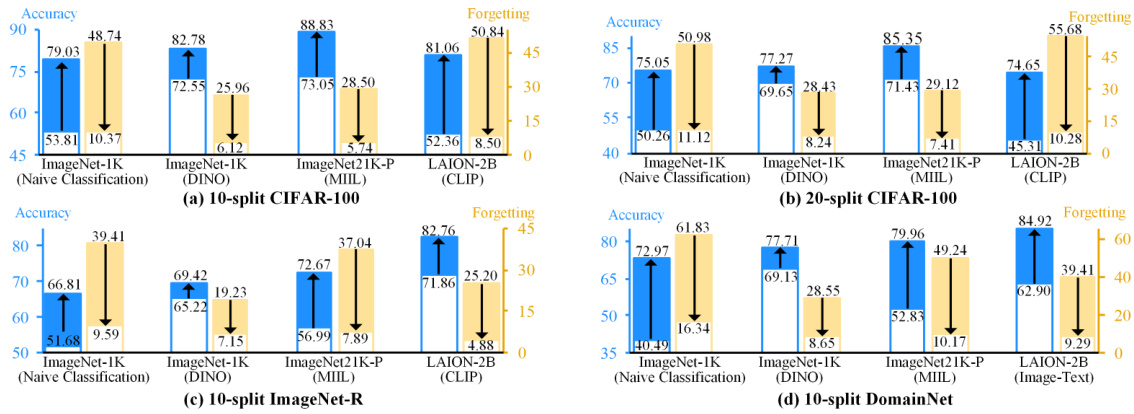
🔼 This figure presents the results of experiments using different pre-trained models and datasets. The models were fine-tuned using the proposed method (VPT-NSP2) and a baseline sequential fine-tuning method (VPT-Seq). The results are shown for four datasets: 10-split and 20-split CIFAR-100, 10-split ImageNet-R, and 10-split DomainNet. Each bar graph represents a dataset, with different pre-training methods shown on the x-axis. The blue bars represent the accuracy, while the yellow bars show the amount of forgetting that occurred during training. Upward-pointing arrows highlight improvements in accuracy with the proposed method compared to the baseline, while downward-pointing arrows indicate reductions in forgetting.

read the caption

Figure 3: Results of utilizing different pre-training datasets and paradigms. The blue and yellow bars represent accuracy and forgetting, respectively. The upward arrows indicate the accuracy increasing from VPT-Seq to VPT-NSP2, whereas the downward arrows denote the reduction in forgetting.

🔼 This figure shows the task-by-task accuracy curves for both the sequential fine-tuning baseline (VPT-Seq) and the proposed Null-Space Projection for Prompts (VPT-NSP2) method. The plots visually demonstrate the effectiveness of VPT-NSP2 in maintaining high accuracy on previously learned tasks while learning new ones. The downward-pointing arrows highlight the significant reduction in forgetting achieved by VPT-NSP2 compared to VPT-Seq. Two different benchmark datasets are presented: 10-split CIFAR-100 and 10-split ImageNet-R.

read the caption

Figure 2: Task-by-task accuracy changing curves of VPT-Seq and VPT-NSP2 on two benchmarks.

🔼 This figure illustrates the forward propagation process within a single ViT layer, focusing on how input image tokens and prompts interact. It shows the steps involved: Layer Normalization (LN), linear transformations (qkv), self-attention (including affinity, softmax, and aggregation), and finally the MLP layer. Crucially, it highlights that certain elements (rows of the attention map related to prompts as queries, and output prompts) can be effectively ignored during training because they don’t directly influence the image tokens. This simplification is key to understanding the proposed approach in the paper.

read the caption

Figure 1: Illustration of the forward propagation in a ViT layer. Residual connections are omitted. The red crosses indicate the rows of attention map or the output prompts can be neglected.

More on tables

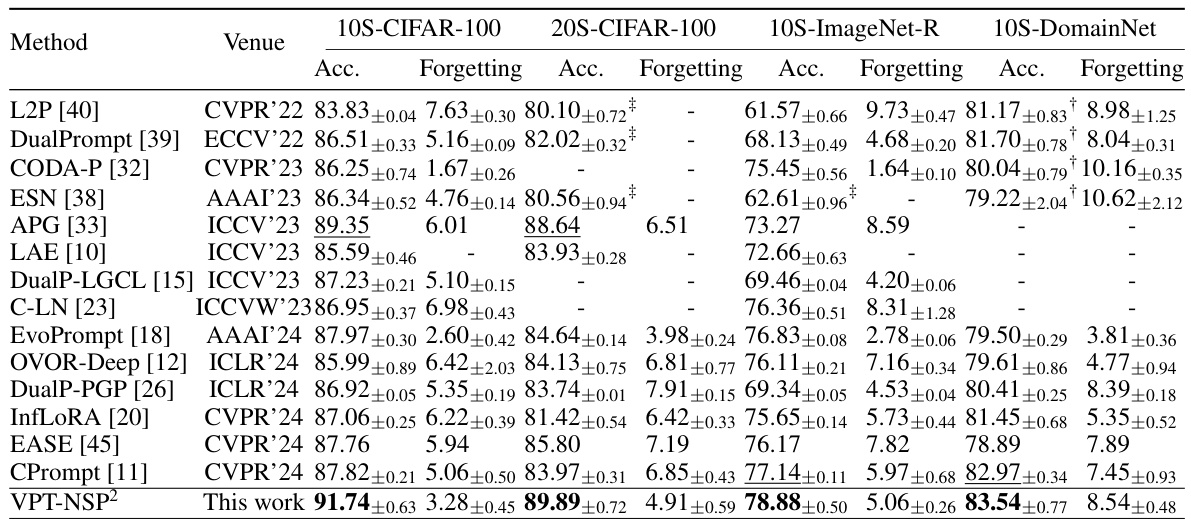
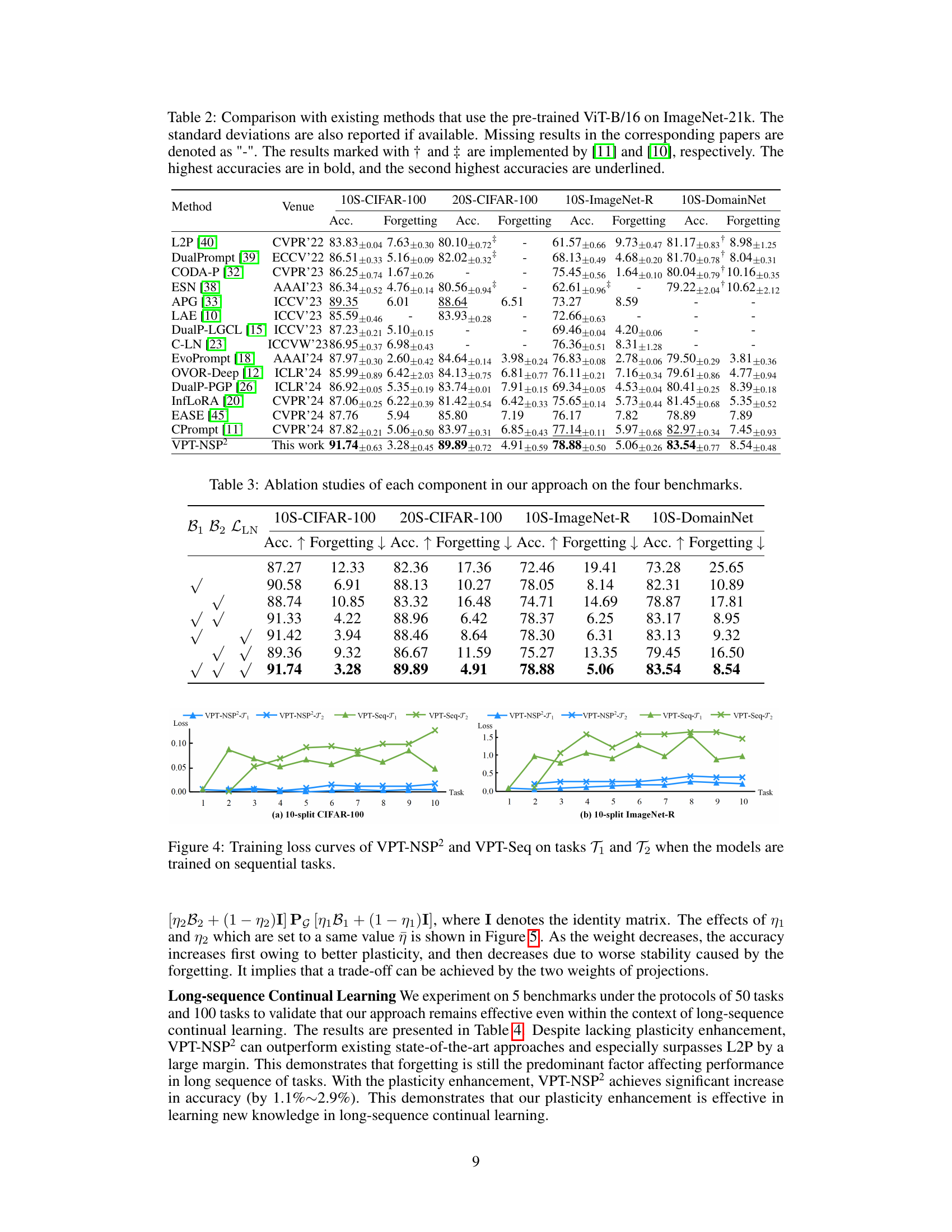
🔼 This table compares the proposed VPT-NSP2 method against other state-of-the-art methods for continual learning using the pre-trained ViT-B/16 model on ImageNet-21k. It shows the accuracy and forgetting rates achieved by each method on four benchmark datasets: 10-split and 20-split CIFAR-100, 10-split ImageNet-R, and 10-split DomainNet. The table highlights the superior performance of VPT-NSP2 in terms of accuracy while maintaining relatively low forgetting rates compared to other approaches.

read the caption

Table 2: Comparison with existing methods that use the pre-trained ViT-B/16 on ImageNet-21k. The standard deviations are also reported if available. Missing results in the corresponding papers are denoted as '-'. The results marked with † and ‡ are implemented by [11] and [10], respectively. The highest accuracies are in bold, and the second highest accuracies are underlined.

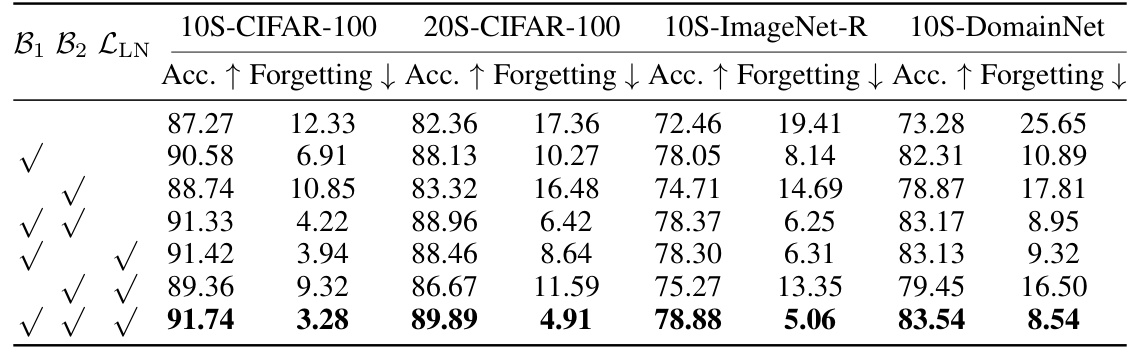
🔼 This table presents a comparison of the proposed method (VPT-NSP2) against two baseline methods (VPT-Seq and CLIP-Seq) across four continual learning benchmarks. The benchmarks utilize two different model architectures: VPT and CLIP. The ‘Forgetting’ column shows the decrease in accuracy on previously seen tasks, illustrating the catastrophic forgetting phenomenon. The ‘Accuracy’ column represents the performance on the current task, showing how well the model performs at learning the new task. The ‘Upper-bound’ row indicates the ideal performance if all classes are trained together from the start, providing a context for understanding the limitations of continual learning scenarios.

read the caption

Table 1: Comparison with the baselines ('-Seq') on four benchmarks using two types of models. The upper-bound means jointly training all the classes in the dataset.

🔼 This table compares the performance of the proposed method (VPT-NSP2) against two baseline methods (VPT-Seq and CLIP-Seq) across four continual learning benchmarks using two different model architectures (VPT and CLIP). It shows the accuracy and forgetting rate for each method on 10-split and 20-split versions of CIFAR-100, 10-split ImageNet-R, and 10-split DomainNet. The ‘upper-bound’ row indicates the performance achieved when training on all classes jointly, providing a reference point for the maximum achievable performance. Lower forgetting rates indicate better ability to retain knowledge from previously learned tasks.

read the caption

Table 1: Comparison with the baselines ('-Seq') on four benchmarks using two types of models. The upper-bound means jointly training all the classes in the dataset.

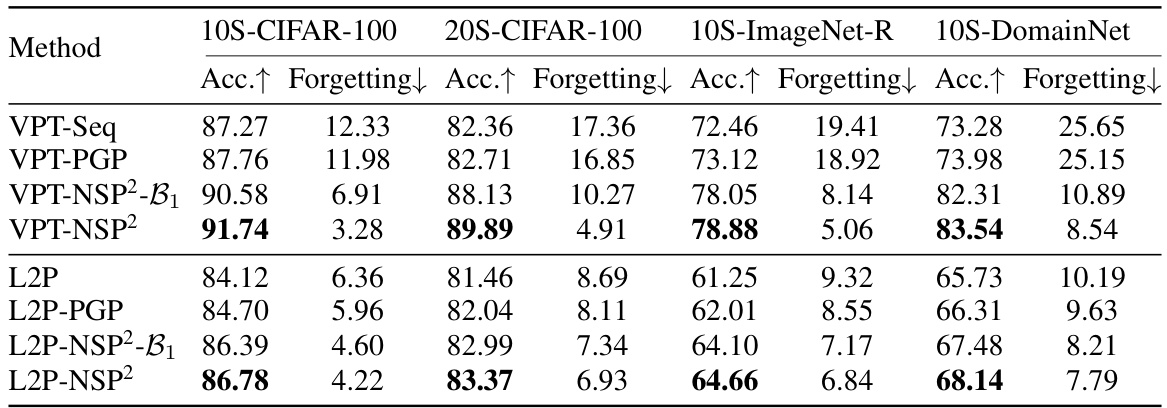
🔼 This table compares the performance of the proposed Null-Space Projection for Prompts (NSP2) method against two baseline methods (VPT-Seq and CLIP-Seq) across four continual learning benchmarks (10S and 20S CIFAR-100, 10S ImageNet-R, and 10S DomainNet). The ‘Seq’ suffix denotes sequential fine-tuning. It presents the accuracy and forgetting rates for each method, showing the improvements achieved by NSP2 in terms of both accuracy and reduction in catastrophic forgetting. The upper-bound column indicates the performance achieved by jointly training on all classes, serving as an upper limit for comparison.

read the caption

Table 1: Comparison with the baselines ('-Seq') on four benchmarks using two types of models. The upper-bound means jointly training all the classes in the dataset.

Full paper

#