TL;DR#
Current LLM self-training methods often struggle with low-quality training data, resulting from inaccurate reasoning steps. This leads to limited performance improvements. Existing approaches often require manual annotation or rely on imperfect reward models.
ReST-MCTS* innovatively uses a modified Monte Carlo Tree Search (MCTS*) algorithm guided by a learned process reward model. This allows for automated generation and annotation of higher-quality reasoning traces. The results demonstrate significant performance gains over previous methods, showcasing its effectiveness in LLM self-training and providing a more efficient way to improve model capabilities. The released code facilitates further research and development in the field.
Key Takeaways#
Why does it matter?#
This paper is crucial because it presents a novel self-training approach for LLMs that addresses the limitations of existing methods. By using process reward guidance and tree search, it generates higher-quality training data, leading to improved performance. This work significantly contributes to the ongoing research in LLM self-improvement and opens new avenues for future investigations.
Visual Insights#
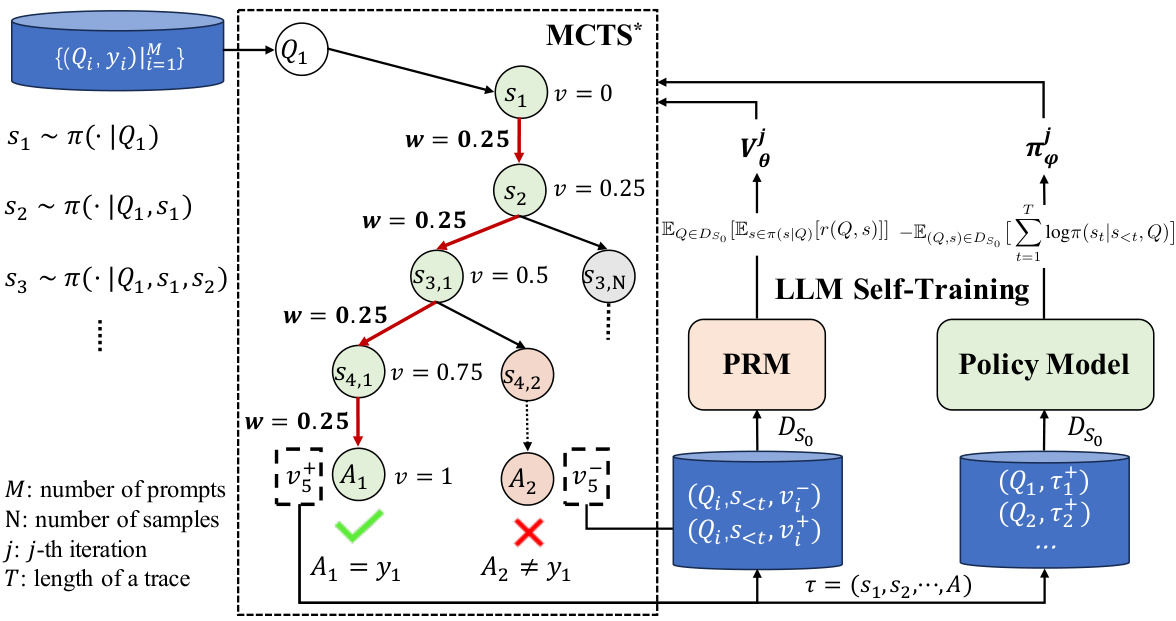
🔼 This figure illustrates the ReST-MCTS* framework. The left side shows how process rewards are inferred using a Monte Carlo Tree Search (MCTS*) algorithm guided by a process reward model (PRM). The PRM estimates the probability that a given step will lead to a correct answer. These inferred rewards are used as value targets for refining the PRM and selecting high-quality reasoning traces. The right side details the self-training process, showing how the PRM and policy model are iteratively improved using the traces generated by the MCTS*. This iterative process leads to continuously enhanced language models.
read the caption
Figure 1: The left part presents the process of inferring process rewards and how we conduct process reward guide tree-search. The right part denotes the self-training of both the process reward model and the policy model.
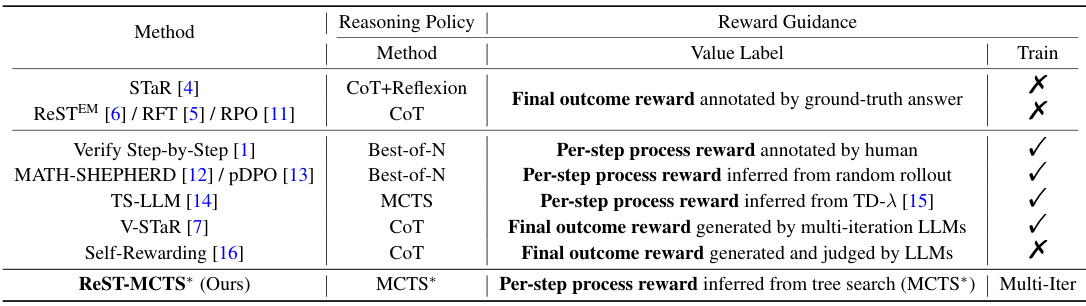
🔼 This table compares several existing self-improvement methods for LLMs with the proposed ReST-MCTS*. It highlights key differences in reasoning policy methods (e.g., Chain of Thought, Best-of-N, MCTS), reward guidance (e.g., final outcome reward, per-step process reward), the source of reward labels (e.g., human annotation, ground-truth, inferred), and whether a reward model was trained. The table shows that ReST-MCTS* differs from previous methods by using process rewards inferred from tree search and employing multi-iterative training for both policy and reward models.
read the caption
Table 1: Key differences between existing self-improvement methods and our approach. Train refers to whether to train a reward model.
In-depth insights#
Process Reward MCTS*#
The proposed ‘Process Reward MCTS*’ method represents a novel approach to LLM self-training. It intelligently combines the power of Monte Carlo Tree Search (MCTS) with a process reward model to overcome limitations of existing self-training techniques that often yield low-quality training data. MCTS is used not only for efficient search but also for automatically generating per-step reward labels*, eliminating the need for manual annotation. This automated process is crucial for scaling. The algorithm iteratively refines both a policy model (for generating reasoning steps) and a process reward model (for evaluating the quality of these steps). This mutual self-training loop continuously enhances the LLM’s reasoning abilities by focusing on high-quality reasoning traces. The method’s effectiveness is supported by experimental results demonstrating superior performance compared to existing methods, particularly regarding accuracy and the efficient use of search budget. The key innovation lies in the automatic annotation of process rewards, enabling continuous self-improvement without human intervention. This approach presents a significant advancement in LLM self-training, paving the way for more efficient and robust methods.
LLM Self-Training#
LLM self-training represents a paradigm shift in large language model development, moving away from the reliance on solely human-generated data. The core challenge lies in creating effective reward mechanisms to guide the learning process, as manually annotating LLM-generated text is impractical at scale. This paper introduces ReST-MCTS*, a novel approach that leverages process reward guidance within a Monte Carlo Tree Search (MCTS) algorithm* to automatically infer per-step rewards. This circumvents the need for manual annotation, enabling the creation of higher-quality training data. The dual purpose of inferred rewards – refining the process reward model and guiding tree search – is a significant contribution. By utilizing traces generated by this refined policy, the method facilitates continuous LLM self-improvement, outperforming other self-training techniques like ReSTEM and Self-Rewarding LM. The automated generation of high-quality traces is a key advantage, directly addressing the limitations of prior methods that often rely on selecting final outputs rather than evaluating the entire reasoning process.
Iterative Refinement#
Iterative refinement, in the context of large language model (LLM) self-training, represents a crucial process for enhancing model capabilities. It involves a cyclical process of generating data, evaluating its quality, and using the feedback to improve the model’s parameters. This iterative approach is essential because LLMs, when generating data for self-training, often produce outputs of varying quality. The iterative refinement approach helps to filter out low-quality data and retain only the high-quality samples, which leads to more effective fine-tuning. Each iteration refines the model, leading to improved reasoning abilities and higher-quality data generation in the subsequent cycle. The core of iterative refinement lies in incorporating feedback loops, which allow for continuous adaptation and optimization. This approach contrasts with single-step training methods, which lack the ability to adjust and improve based on performance. Effective evaluation metrics are critical for guiding the refinement process. These metrics must accurately reflect the quality of the generated data and the model’s performance on relevant tasks. Through iterative refinement, LLMs can progressively improve their capabilities, leading to more sophisticated and accurate reasoning abilities.
Benchmark Results#
A thorough analysis of benchmark results is crucial for evaluating the effectiveness of a novel approach. It’s important to understand what benchmarks were used, why those specific benchmarks were chosen, and what metrics were used to measure performance. A strong analysis will also address the limitations of the chosen benchmarks, and discuss how the results compare to those of existing methods. Specific details about the experimental setup are important, such as the hardware and software used, the datasets employed, and any pre-processing steps taken. Statistical significance of the results should be established, and any potential biases should be discussed. A comparison to existing state-of-the-art methods provides crucial context and demonstrates the advancement achieved. Clearly presenting the results in tables and figures, along with a detailed description of the findings, is essential. Finally, the discussion section should analyze what the benchmark results indicate about the underlying reasons for success or failure, offering insights into the nature of the proposed approach and its strengths and weaknesses.
Future Research#
Future research directions stemming from this work on ReST-MCTS* for LLM self-training could explore several promising avenues. Extending the approach to handle tasks without ground truth labels is crucial for broader applicability, potentially leveraging techniques like reinforcement learning from human feedback or self-supervised learning methods. Improving the scalability and efficiency of the MCTS algorithm* is also important; exploring alternative tree search methods or incorporating more sophisticated pruning strategies could significantly reduce computational costs. Investigating the impact of different LLM architectures and sizes on the effectiveness of ReST-MCTS* would provide further insights into its robustness and potential limitations. A comparative analysis of ReST-MCTS against other state-of-the-art self-training methods* on a wider range of benchmark datasets is necessary to solidify its performance claims. Finally, a deeper theoretical understanding of why ReST-MCTS* succeeds and under what conditions it outperforms other techniques could pave the way for even more efficient and effective LLM self-training methods in the future.
More visual insights#
More on figures

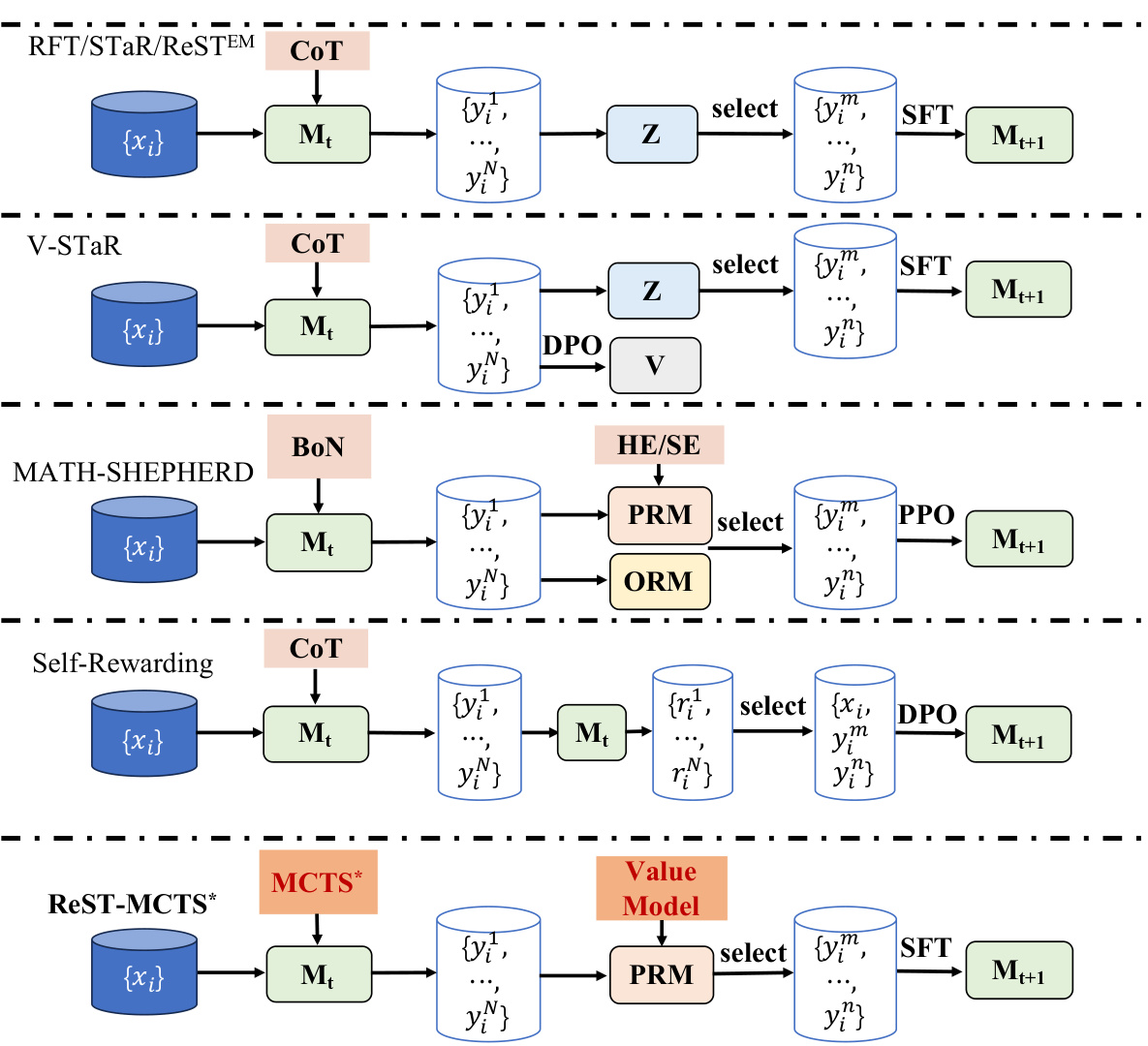
🔼 This figure compares the accuracy of different search methods (ReST-MCTS*, PRM+Best-of-N, ORM+Best-of-N, and Self-Consistency) on the MATH and SciBench datasets. The x-axis represents the average number of completion tokens used per question, which serves as a proxy for the computational budget. The y-axis shows the accuracy achieved by each method. The figure demonstrates that ReST-MCTS* consistently outperforms the other methods across various budget levels, highlighting its efficiency in finding accurate solutions.
read the caption
Figure 2: Accuracy of different searches on MATH and SciBench with varied sampling budget.
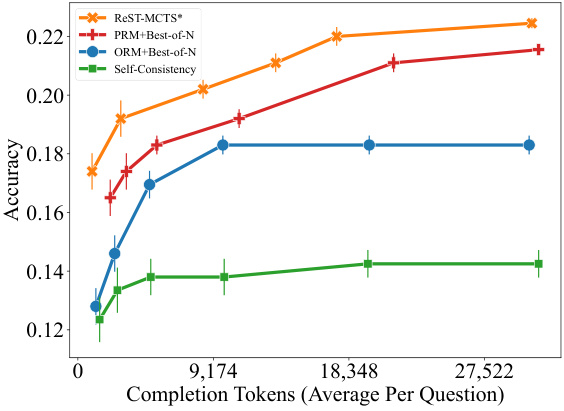
🔼 This figure compares the accuracy of different search methods (ReST-MCTS*, PRM+Best-of-N, ORM+Best-of-N, and Self-Consistency) on two datasets (MATH and SciBench) with varying completion token budgets. It shows that ReST-MCTS* consistently outperforms other methods, particularly as the token budget increases. The error bars represent the variability in accuracy across multiple runs for each method.
read the caption
Figure 2: Accuracy of different searches on MATH and SciBench with varied sampling budget.

🔼 This figure illustrates the ReST-MCTS* framework. The left side shows how process rewards are inferred using a tree search algorithm (MCTS*) and used to guide the search process. The right side illustrates the iterative self-training process for both the process reward model (PRM) and the policy model. The PRM learns to estimate the probability that a given step will lead to the correct answer, while the policy model learns to generate high-quality reasoning traces. The interaction between these two models drives continuous improvement in the LLM’s reasoning abilities.
read the caption
Figure 1: The left part presents the process of inferring process rewards and how we conduct process reward guide tree-search. The right part denotes the self-training of both the process reward model and the policy model.
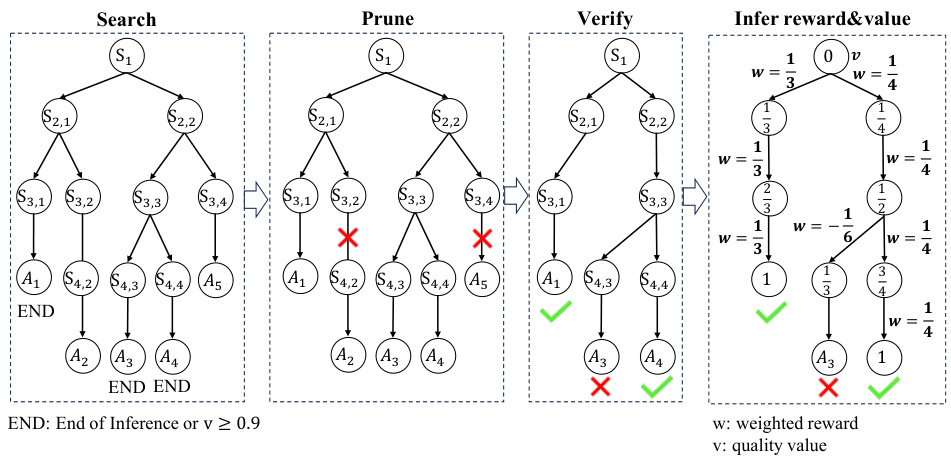
🔼 This figure shows a detailed illustration of the data generation process for the self-training framework. It consists of four stages: search, prune, verify, and infer reward & value. The search stage involves using MCTS* to explore the search space and generate multiple reasoning traces. The prune stage involves removing unfinished branches and those with incorrect final answers. The verify stage involves verifying the correctness of the remaining traces using string matching or LLM judging. Finally, the infer reward & value stage involves inferring the per-step process rewards and quality values for each step in the verified reasoning traces. These inferred rewards and values are then used to train the process reward and policy models.
read the caption
Figure 4: Detailed process of new sample data generation for the self-training framework.
🔼 This figure compares the accuracy of different search methods (ReST-MCTS*, PRM+Best-of-N, ORM+Best-of-N, and Self-Consistency) on two datasets, MATH and SciBench. The x-axis represents the average number of completion tokens used per question, indicating the computational cost of each method. The y-axis shows the accuracy achieved by each method. The figure demonstrates that ReST-MCTS* consistently outperforms other methods across different token budgets, highlighting its efficiency in finding accurate solutions.
read the caption
Figure 2: Accuracy of different searches on MATH and SciBench with varied sampling budget.
🔼 This figure compares the proposed ReST-MCTS* self-training method with other existing methods such as RFT/STaR/ReSTEM, V-STaR, MATH-SHEPHERD, and Self-Rewarding. It visually depicts the flow of each method, highlighting key components like the reasoning policy used (CoT, ToT, BoN, MCTS*), reward models (PRM, ORM), selection mechanisms (select), and fine-tuning steps (SFT). The figure effectively illustrates the differences in how each approach generates training data and improves the language model. ReST-MCTS* stands out by incorporating a value model guided MCTS* for automated per-step reward generation and improved trace selection, leading to a more efficient and effective self-training process.
read the caption
Figure 6: Comparison between existing self-training methods with our proposed ReST-MCTS*.

🔼 This figure illustrates the ReST-MCTS* framework. The left side shows how process rewards are inferred using Monte Carlo Tree Search (MCTS*) and used to guide the tree search. The right side depicts the iterative self-training process for both the process reward model and the policy model, improving the accuracy and quality of reasoning traces over multiple iterations.
read the caption
Figure 1: The left part presents the process of inferring process rewards and how we conduct process reward guide tree-search. The right part denotes the self-training of both the process reward model and the policy model.
More on tables
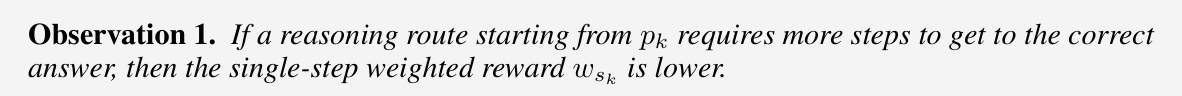
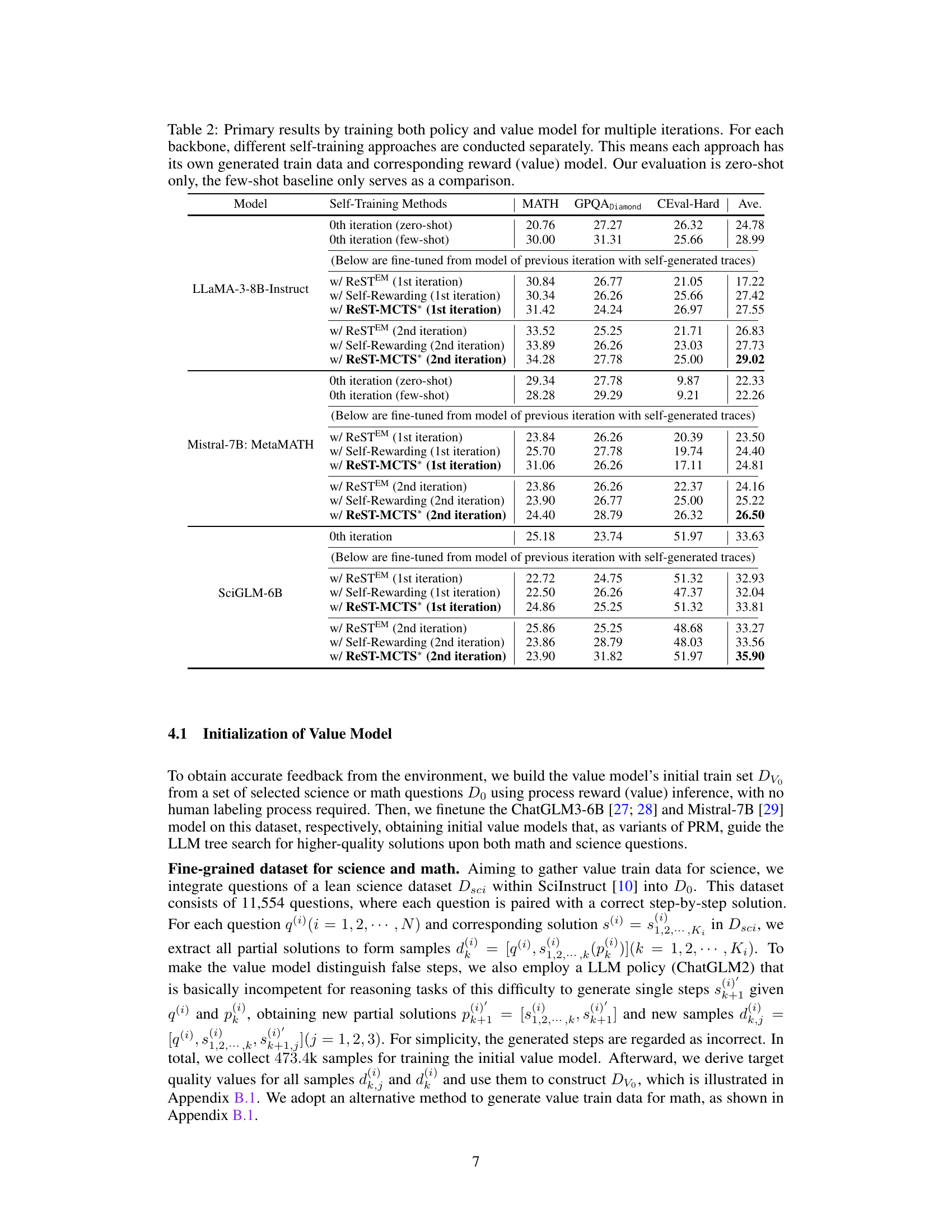
🔼 This table presents the results of training policy and value models across multiple iterations using various self-training methods. It compares the performance of ReST-MCTS* against ReSTEM and Self-Rewarding methods on three different LLM backbones (LLaMA-3-8B-Instruct, Mistral-7B: MetaMATH, and SciGLM-6B). The evaluation is zero-shot, with few-shot results provided as a baseline. The table highlights the continuous improvement of ReST-MCTS* across iterations.
read the caption
Table 2: Primary results by training both policy and value model for multiple iterations. For each backbone, different self-training approaches are conducted separately. This means each approach has its own generated train data and corresponding reward (value) model. Our evaluation is zero-shot only, the few-shot baseline only serves as a comparison.

🔼 This table presents the results of experiments comparing different self-training approaches across multiple iterations. The approaches are evaluated using three different Large Language Model (LLM) backbones: LLaMA-3-8B-Instruct, Mistral-7B, and SciGLM-6B. Each approach undergoes two iterations of self-training, and results are shown for zero-shot and few-shot evaluations. The metrics used include MATH, GPQA, Diamond, and CEval-Hard, providing a comprehensive comparison of the performance of different methods.
read the caption
Table 2: Primary results by training both policy and value model for multiple iterations. For each backbone, different self-training approaches are conducted separately. This means each approach has its own generated train data and corresponding reward (value) model. Our evaluation is zero-shot only, the few-shot baseline only serves as a comparison.
🔼 This table presents the zero-shot and few-shot experimental results of three different LLMs (LLaMA-3-8B-Instruct, Mistral-7B: MetaMATH, and SciGLM-6B) across various self-training methods (ReSTEM, Self-Rewarding, and ReST-MCTS*) over two iterations. It shows how each self-training method performs on MATH, GPQA, Diamond, and CEval-Hard benchmarks and highlights the continuous improvement of ReST-MCTS* across iterations.
read the caption
Table 2: Primary results by training both policy and value model for multiple iterations. For each backbone, different self-training approaches are conducted separately. This means each approach has its own generated train data and corresponding reward (value) model. Our evaluation is zero-shot only, the few-shot baseline only serves as a comparison.

🔼 This table compares the accuracy of different verification methods (Self-Consistency, Outcome Reward Model, Self-Consistency + Outcome Reward Model, MATH-SHEPHERD, Self-Consistency + MATH-SHEPHERD, and Self-Consistency + ReST-MCTS*) on two datasets (GSM8K and MATH500). Each method’s accuracy is evaluated based on 256 outputs. The table highlights the superior performance of ReST-MCTS* in achieving higher accuracy on both datasets.
read the caption
Table 3: Accuracy of different verifiers on GSM8K test set and MATH500. SC: Self-Consistency, MS: MATH-SHEPHERD. Verification is based on 256 outputs.
🔼 This table presents the results of training both the policy and value models for multiple iterations using different self-training methods. The performance is evaluated using zero-shot settings on several benchmarks, comparing against a few-shot baseline. Each self-training method uses its own generated training data and corresponding reward model.
read the caption
Table 2: Primary results by training both policy and value model for multiple iterations. For each backbone, different self-training approaches are conducted separately. This means each approach has its own generated train data and corresponding reward (value) model. Our evaluation is zero-shot only, the few-shot baseline only serves as a comparison.
🔼 This table compares the proposed ReST-MCTS* approach with existing LLM self-improvement methods such as STaR, ReSTEM, RFT, and V-STaR. The comparison highlights key differences in reasoning policies (e.g., whether they use chain-of-thought, best-of-N, or Monte Carlo Tree Search), reward guidance (type of reward signals used), and whether a reward model is trained. ReST-MCTS* is shown to be unique in its use of process reward guidance with MCTS* for collecting high-quality reasoning traces.
read the caption
Table 1: Key differences between existing self-improvement methods and our approach. Train refers to whether to train a reward model.

🔼 This table presents the average running time, in seconds, for four different reasoning methods: CoT + SC, ORM + BoN, PRM + BoN, and MCTS*. The times are broken down for MATH problems. It highlights the computational cost differences between the methods, showing that MCTS* requires significantly more time than the others.
read the caption
Table 6: The average running time of different algorithms (under our basic experiment settings) on a single question.
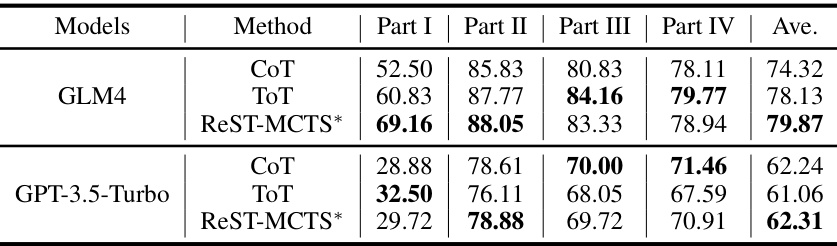
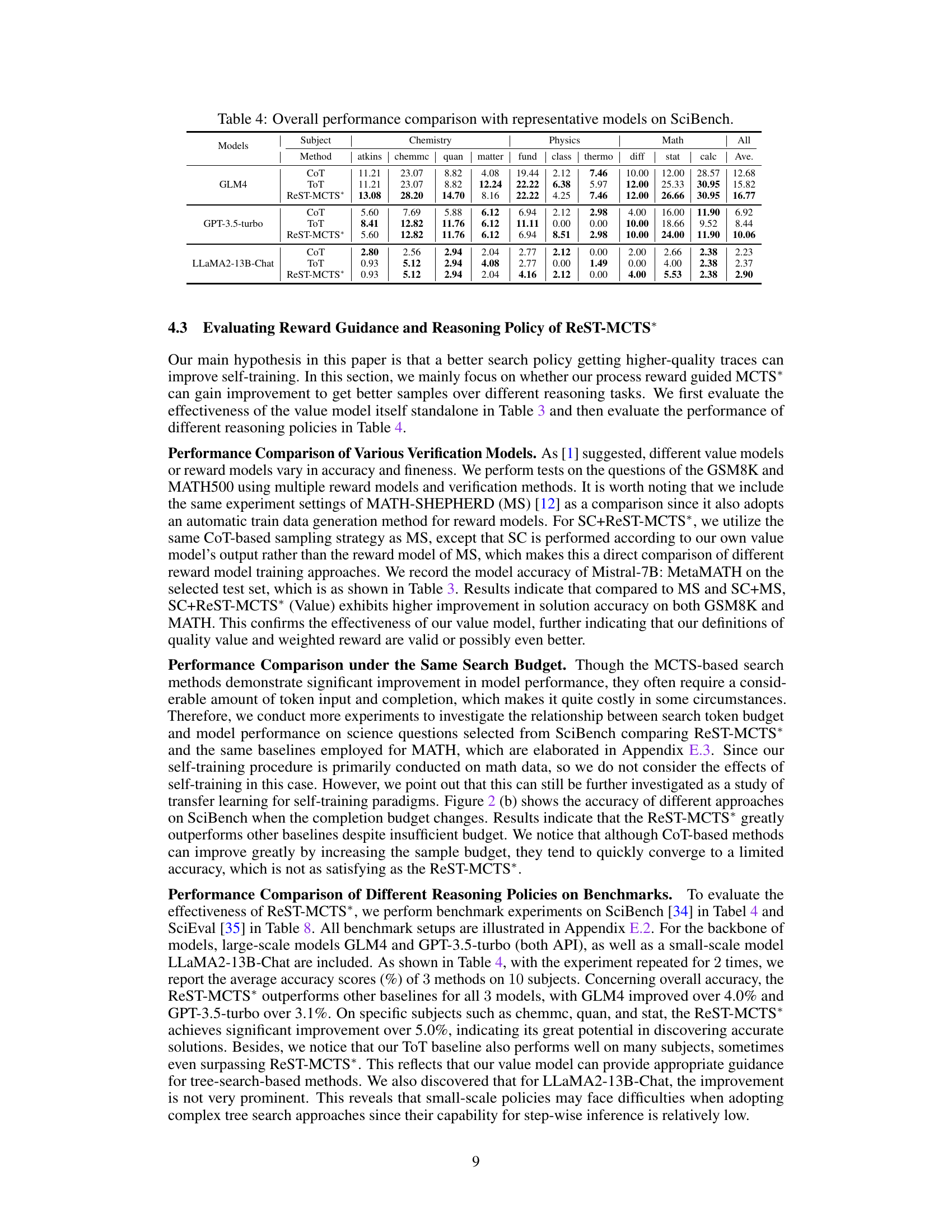
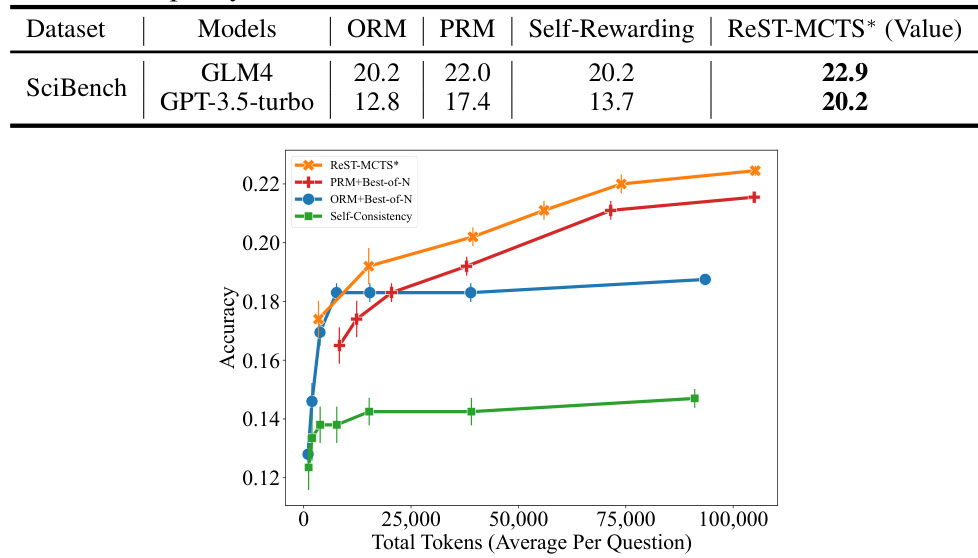
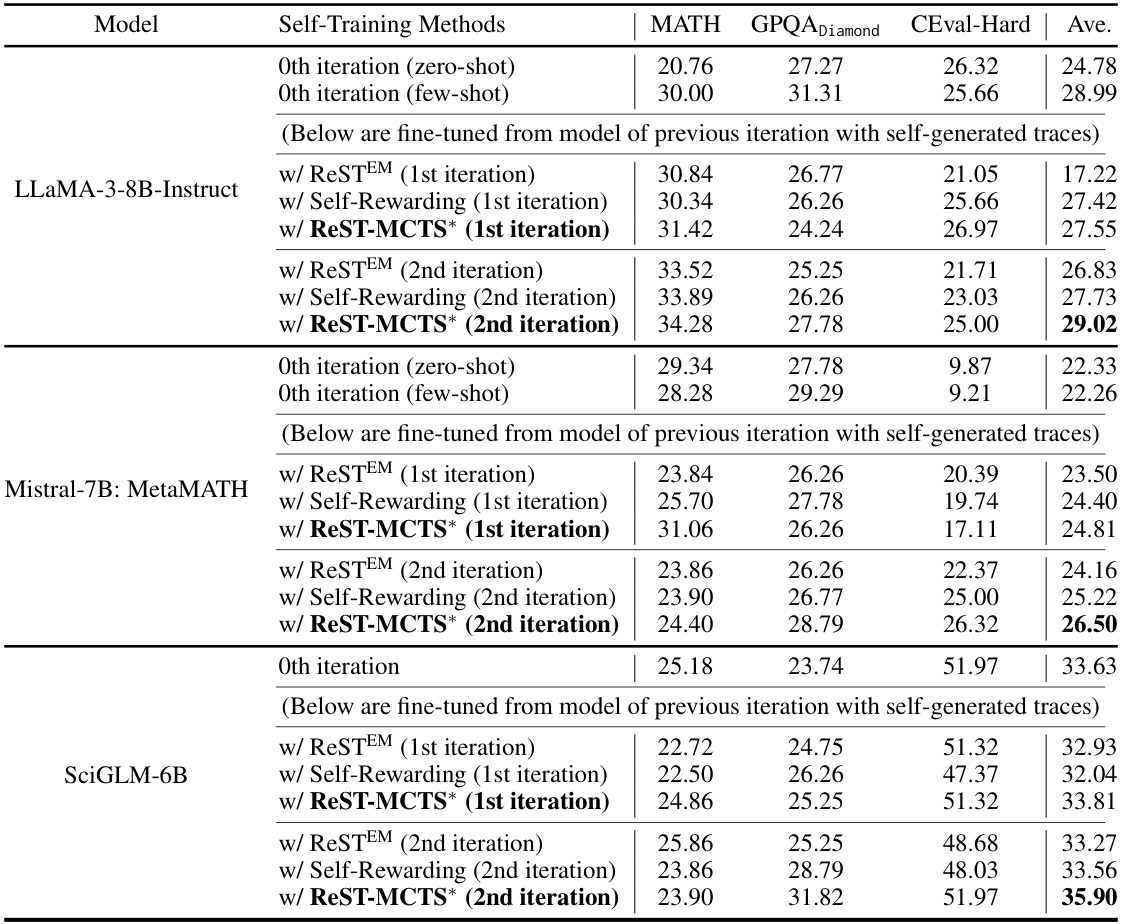
🔼 This table presents a comparison of the overall performance of three different reasoning methods (CoT, ToT, and ReST-MCTS*) on the SciEval benchmark. The results are broken down by four parts of the benchmark (Part I, Part II, Part III, Part IV) and an overall average. The table shows the performance of these methods using two different large language models (LLMs): GLM4 and GPT-3.5-Turbo. The purpose is to demonstrate the superior performance of the ReST-MCTS* method compared to other more traditional reasoning methods.
read the caption
Table 8: Overall performance comparison with representative models on SciEval.
Full paper#