TL;DR#
Reinforcement Learning (RL) traditionally focuses on minimizing cumulative costs. However, real-world scenarios demand robustness against environmental changes and uncertainties, necessitating the use of more general utility functions that capture various objectives beyond simple cost minimization. Existing RL methods often lack this robustness and struggle with general utility functions. This makes their applicability to real-world problems limited.
This research tackles this challenge head-on by introducing a new robust RL framework that handles general utility functions and accounts for environmental perturbations. The researchers propose novel two-phase stochastic gradient algorithms that are provably convergent, meaning they reliably find optimal or near-optimal solutions. Furthermore, they provide strong theoretical guarantees on convergence rates and achieve global optimality in specific cases (convex utility functions and polyhedral ambiguity sets). This significantly enhances the reliability and adaptability of RL agents in dynamic and uncertain environments.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning because it addresses the critical issue of robustness in real-world applications. By extending existing frameworks to handle general utility functions and environmental uncertainty, it opens doors for more reliable and adaptable RL agents. The proposed algorithms and theoretical analysis offer valuable tools for designing robust and efficient RL systems, paving the way for more practical applications in various fields.
Visual Insights#
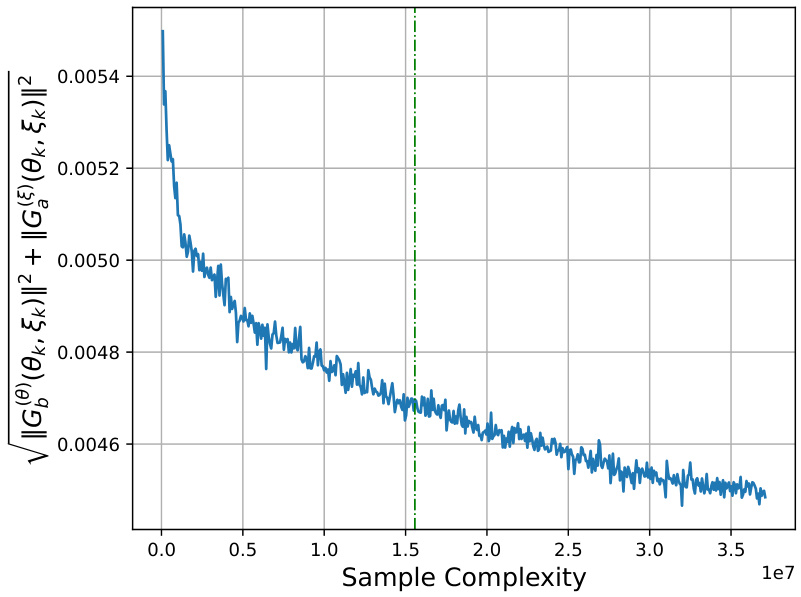
🔼 The figure shows the numerical experimental result of Algorithm 1. The y-axis represents the norm of the true projected gradient at each iteration, and the x-axis represents the sample complexity. The green vertical dashed line indicates the transition point between Phase I and Phase II of Algorithm 1. The result shows that the projected gradient decays and converges to a small value, which matches the theoretical result of Theorem 2 in the paper.
read the caption
Figure 1: Numerical Experimental Result (the green vertical line denotes the transition from Phase I to Phase II of Algorithm 1).
Full paper#