TL;DR#
Multi-task learning (MTL) aims to improve efficiency and generalization by training multiple tasks simultaneously. However, task imbalance, where some tasks significantly underperform, hinders MTL’s effectiveness. Existing methods struggle to achieve both high performance and computational efficiency; gradient-oriented methods excel in performance but are computationally expensive, while loss-oriented methods prioritize efficiency over performance.
GO4Align, a new loss-oriented MTL approach, tackles task imbalance by explicitly aligning optimization across tasks. This is achieved using an adaptive group risk minimization strategy, comprising (i) dynamical group assignment clustering similar tasks, and (ii) risk-guided group indicators using consistent task correlations. Extensive experiments demonstrate GO4Align’s superior performance and even lower computational costs compared to current state-of-the-art methods across diverse benchmarks.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces GO4Align, a novel multi-task optimization approach that effectively tackles task imbalance, a common challenge in multi-task learning. It offers a computationally efficient solution by dynamically aligning learning progress across tasks, significantly improving performance compared to existing methods. This opens new avenues for research in adaptive task weighting and efficient multi-task optimization, impacting various machine learning applications.
Visual Insights#

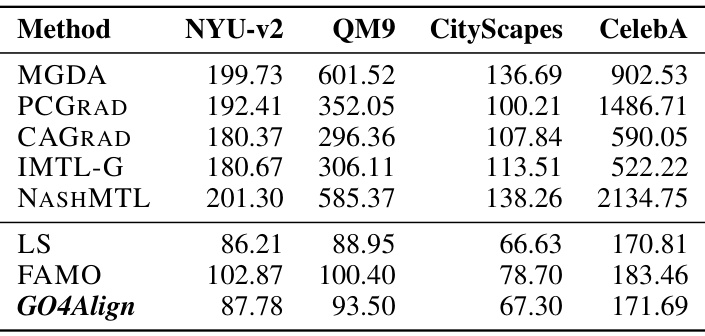
🔼 This figure compares different Multi-Task Optimization (MTO) methods on the NYUv2 dataset. It shows a scatter plot with the relative training time on the x-axis and the change in multi-task performance (Δm%) relative to a baseline method on the y-axis. Each point represents a different MTO method, categorized as gradient-oriented, loss-oriented, or the authors’ proposed method (GO4Align). The plot visually demonstrates that GO4Align achieves superior performance compared to most other methods while maintaining comparable or even lower computational costs. The lower left corner represents the ideal point of faster training and better performance.
read the caption
Figure 1: Performance and computational efficiency evaluation for MTO methods evaluated on NYUv2. Each method's training time is relative to a baseline method, which minimizes the sum of task-specific empirical risks. Left-bottom marks comprehensive optimal results.
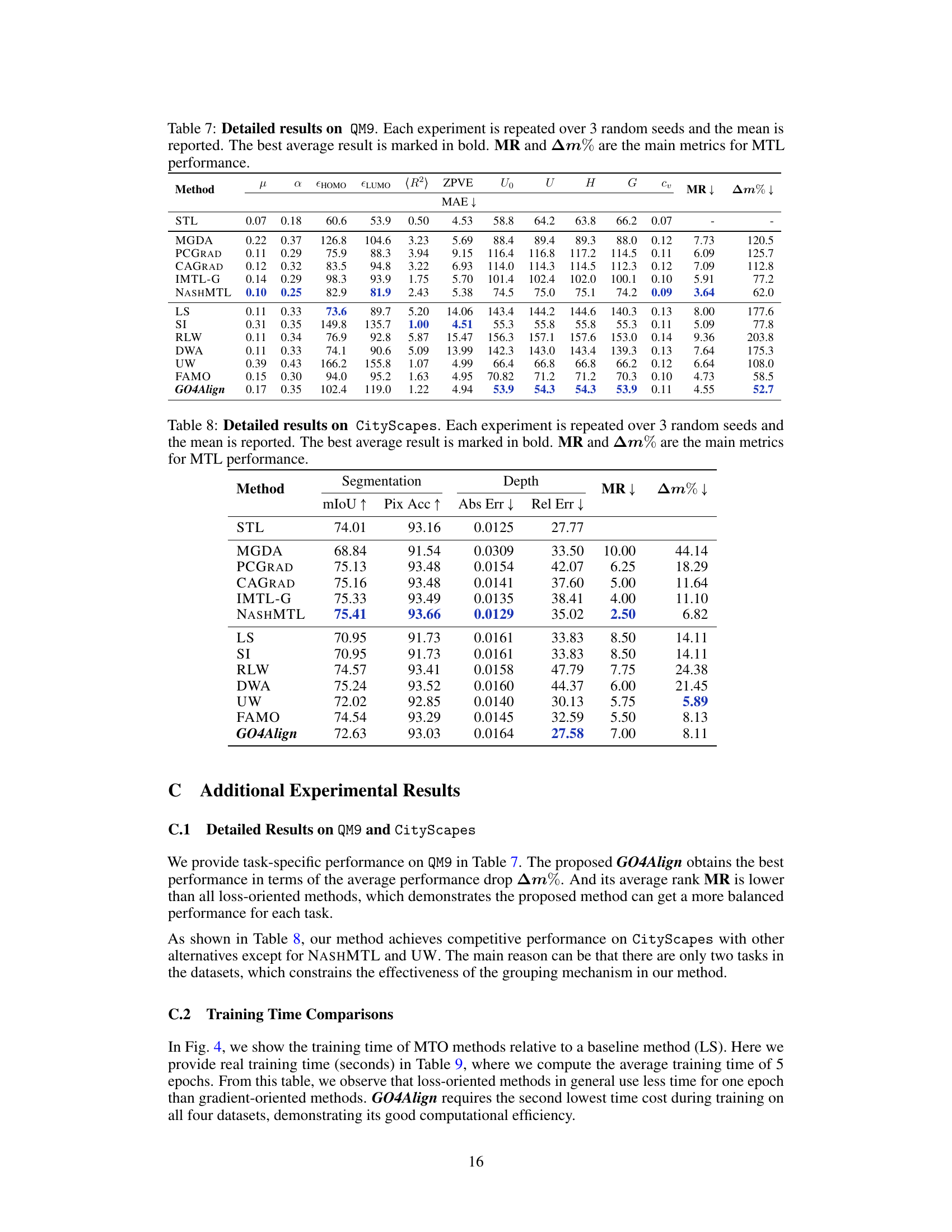
🔼 This table presents the results of the experiments conducted on the NYUv2 dataset, which involves three tasks. It compares various multi-task learning methods, categorized as gradient-oriented and loss-oriented. The table shows performance metrics (mIoU, PixAcc, AbsErr, RelErr, AngleDist, Mean, Median, Within t°, MR, Am%) for each method, averaged over three random seed runs to ensure reliability. The best performing method for each metric is highlighted in bold. MR and Am% are key metrics summarizing overall multi-task learning performance; lower values are better for the metrics denoted by ↓.
read the caption
Table 1: Results on NYUv2 (3 tasks). The upper and lower tables categorize baseline methods into gradient-oriented and loss-oriented types, respectively. Each experiment is repeated over 3 random seeds, and the mean is reported. The best average result is marked in bold. MR and Am% are the main metrics for overall MTL performance. Metrics with↓ denote that the lower the better.
In-depth insights#
Adaptive Risk Minimization#
Adaptive risk minimization, in the context of multi-task learning, tackles the challenge of task imbalance where some tasks may converge faster than others. It aims to dynamically adjust the optimization process, preventing under-optimization of slower tasks while maintaining efficiency. This adaptability is crucial because static weighting schemes often fail to account for the varying learning dynamics of individual tasks. Efficient implementation is key; it should leverage task relationships and risk information to guide the adaptation without requiring computationally expensive per-task gradient calculations. A successful approach would likely involve clustering similar tasks to encourage positive transfer and shared learning, coupled with a mechanism that dynamically allocates weights based on each task’s current progress and inter-task relationships. The overall aim is to achieve faster and more balanced convergence across all tasks, leading to improved overall performance.
Dynamic Group Assign#
The heading ‘Dynamic Group Assignment’ suggests a method for adaptively clustering tasks during multi-task learning. Instead of statically assigning tasks to groups, this approach likely uses a process that adjusts group membership over time based on performance and interactions between tasks. This dynamism is crucial because task relationships and optimal groupings might evolve as the model trains. The algorithm probably leverages metrics such as task loss or gradient similarity to determine which tasks should be grouped together at each iteration. By dynamically adjusting group assignments, the method aims to maximize positive transfer between similar tasks while minimizing negative transfer between dissimilar ones. This approach is likely designed to improve the overall efficiency and effectiveness of multi-task learning by better adapting to changing task relationships during training.
Multi-Task Alignment#
Multi-task learning (MTL) often struggles with task imbalance, where some tasks progress faster than others, hindering overall performance. Multi-task alignment directly addresses this by aiming for synchronized learning progress across all tasks. This requires strategies that go beyond simple loss weighting or gradient manipulation. Effective alignment necessitates understanding and leveraging task relationships. Dynamical group assignment, clustering similar tasks based on their interactions, is a key enabler, allowing for more efficient resource allocation and positive transfer. Further enhancement comes from risk-guided group indicators, which dynamically adjust weights based on the current learning progress and past task correlations. This creates an adaptive system that dynamically adjusts to shifting task relationships, leading to improved overall performance and efficiency. In essence, successful multi-task alignment is about achieving a balance between individual task optimization and global task synchronization, capitalizing on shared structures and avoiding negative transfer.
Efficiency & Scalability#
A crucial aspect of any machine learning model is its efficiency and scalability. Efficiency refers to the model’s computational cost, encompassing training time and memory usage. A highly efficient model minimizes resource consumption, making it suitable for deployment on resource-constrained devices or large-scale applications. Scalability, on the other hand, addresses the model’s ability to handle increasing amounts of data and computational demands. A scalable model maintains performance as the dataset size grows, allowing for the analysis of massive datasets and the training of more complex models. Balancing efficiency and scalability is a significant challenge. Optimization techniques such as model compression, efficient algorithms, and distributed training are vital for achieving both. The choice of architecture also significantly impacts efficiency and scalability. Considering these factors carefully during the model design and development phases leads to a robust and practical system.
Future Work & Limits#
Future work could explore adapting GO4Align to handle even more complex task relationships, perhaps through hierarchical grouping or more sophisticated methods for capturing task interactions. Investigating the sensitivity of the algorithm to hyperparameter choices, particularly the number of groups (K) and the temperature parameter (β), is also crucial. A thorough comparative analysis against a wider range of state-of-the-art MTO methods on additional benchmark datasets is warranted. Furthermore, examining the algorithm’s scalability and performance on larger datasets and more complex tasks is essential to validate its real-world applicability. Finally, a key limitation involves the heuristic nature of group assignment; future research should aim to develop more principled and data-driven strategies for dynamic task grouping. Addressing these points would strengthen the robustness and generalizability of GO4Align.
More visual insights#
More on figures

🔼 This figure shows the relationship between multi-task alignment and overall performance in multi-task optimization. It presents relative task performance curves over training epochs for three different methods: UW, FAMO, and GO4Align. The curves show that methods with smaller convergence differences (the difference in the number of epochs needed for each task to converge) tend to achieve better overall performance. GO4Align, which explicitly addresses task alignment, demonstrates the smallest convergence difference and the best overall performance.
read the caption
Figure 2: Multi-task alignment and effects on performance. We visualize relative task performance curves (lower is better) over training epochs. Better overall performance usually occurs with lower convergence differences. Our method effectively reduces the convergence difference and achieves a better overall performance.

🔼 This figure compares various Multi-Task Optimization (MTO) methods on the NYUv2 dataset, focusing on their performance (measured by MTL Performance Am, lower is better) and computational efficiency (relative training time, lower is better). The baseline method used for comparison is one that minimizes the sum of individual task risks. The figure highlights that GO4Align achieves superior performance compared to other methods while maintaining comparable computational efficiency. The placement of methods on the chart visually represents a tradeoff between performance and computational cost.
read the caption
Figure 1: Performance and computational efficiency evaluation for MTO methods evaluated on NYUv2. Each method's training time is relative to a baseline method, which minimizes the sum of task-specific empirical risks. Left-bottom marks comprehensive optimal results.

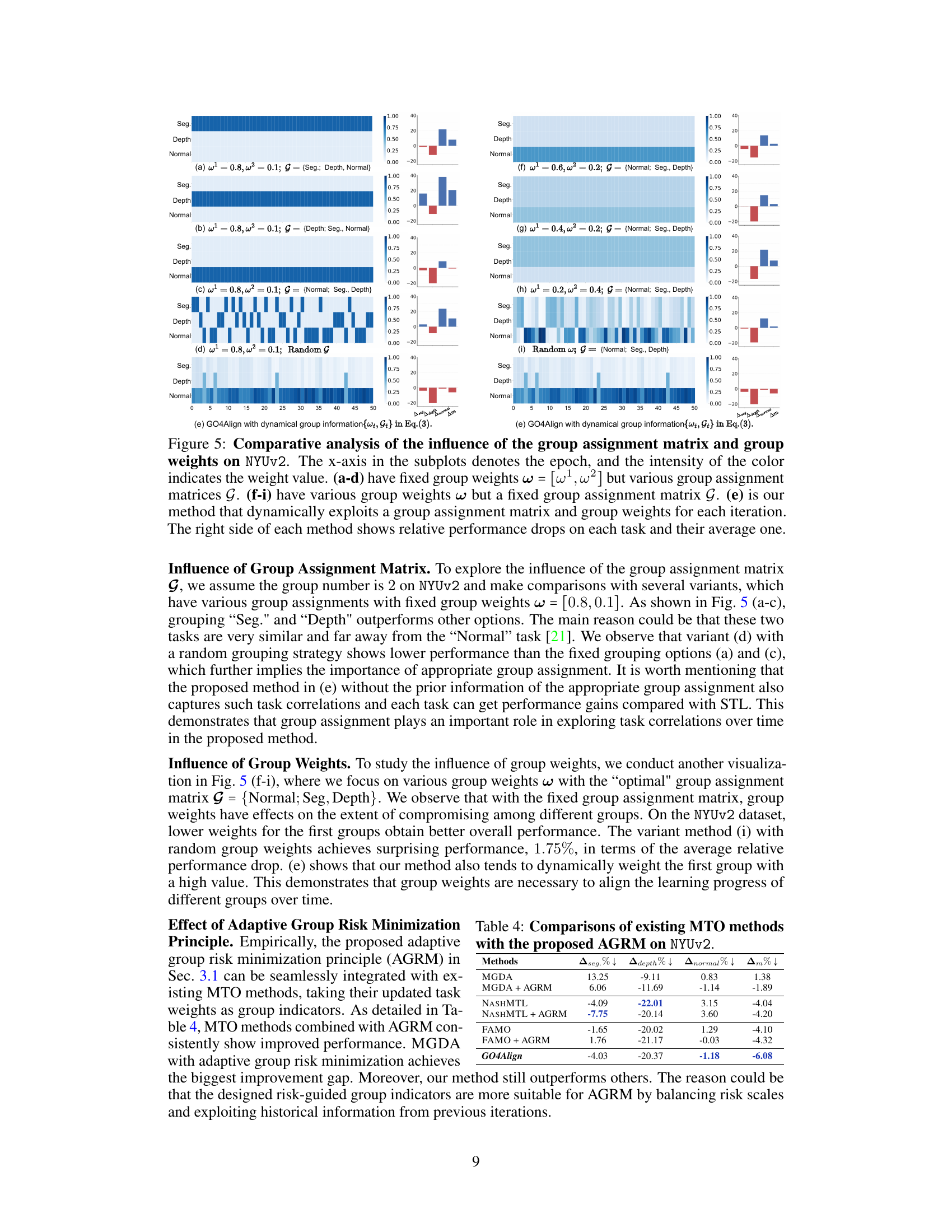
🔼 This figure shows an ablation study on the effects of group assignment matrices and group weights in the GO4Align model. It compares the performance of using fixed weights and varying group assignments (a-d), varying weights and a fixed group assignment (f-i), and the dynamic approach used in the GO4Align model (e). Each subplot shows the learning progress of each task (‘Seg.’, ‘Depth’, ‘Normal’) over epochs. The color intensity represents the weight assigned to each group. The right side of each subplot presents the relative performance drop for each task and the average performance drop.
read the caption
Figure 5: Comparative analysis of the influence of the group assignment matrix and group weights on NYUv2. The x-axis in the subplots denotes the epoch, and the intensity of the color indicates the weight value. (a-d) have fixed group weights w = [w¹, w²] but various group assignment matrices G. (f-i) have various group weights w but a fixed group assignment matrix G. (e) is our method that dynamically exploits a group assignment matrix and group weights for each iteration. The right side of each method shows relative performance drops on each task and their average one.
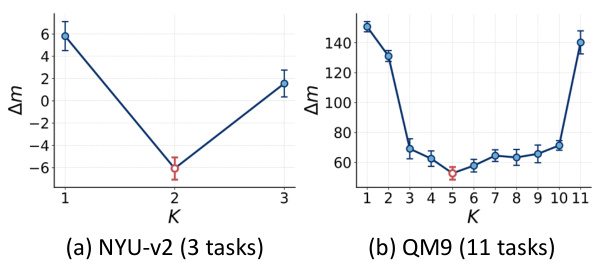
🔼 This figure shows the result of applying the elbow method to determine the optimal number of groups (K) for the NYU-v2 and QM9 datasets. The elbow method is a heuristic used in clustering to identify the optimal number of clusters. The x-axis represents the number of clusters (K), and the y-axis represents the average relative performance drop (Am%). The plot shows that for NYU-v2 (with 3 tasks), the optimal K is 2, while for QM9 (with 11 tasks), the optimal K is 5. The optimal K values are chosen based on the ’elbow’ point of the plot, which represents the point of diminishing returns for increasing the number of clusters.
read the caption
Figure 6: Identification of “elbow” points on NYUv2 and QM9. According to the conventional elbow method, we set the group number of the two datasets as 2 and 5, respectively.
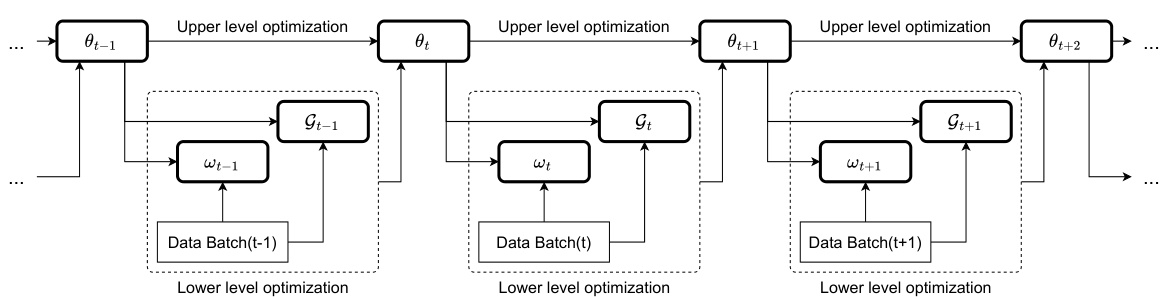
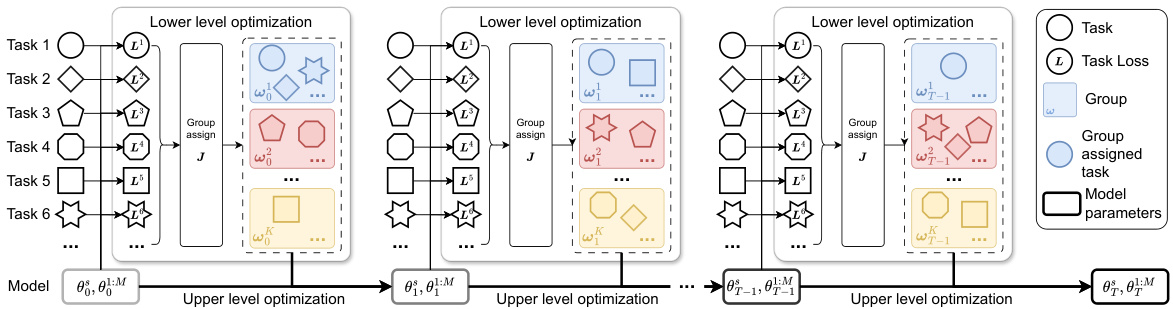
🔼 This figure illustrates the optimization process of GO4Align, which involves a bi-level optimization framework. The lower level focuses on dynamically assigning tasks into groups and determining group weights based on task interactions and learning progress. The upper level utilizes the group information from the lower level to update the model parameters, aligning the learning progress across tasks. The iterative process of lower-level grouping and upper-level parameter updates is visualized, showing how task interactions and risk information from previous iterations influence the task alignment and model learning.
read the caption
Figure 7: Optimization process of the proposed adaptive group risk minimization principle. At each iteration, given the randomly sampled mini-batch data, we first compute the group information w and G in the lower-level optimization and then update the model's parameter θ in the upper-level optimization.

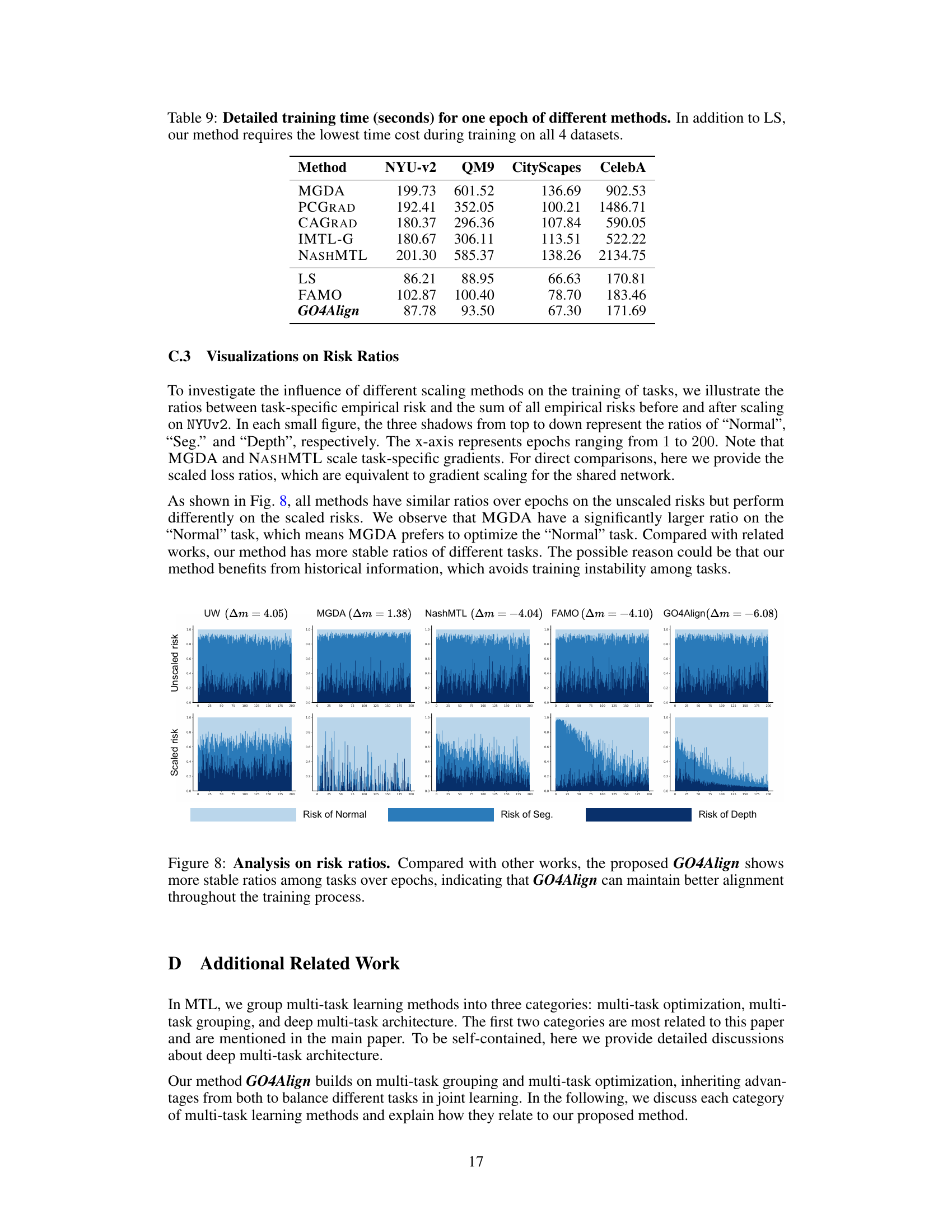
🔼 This figure visualizes the ratios between task-specific empirical risk and the sum of all empirical risks before and after scaling for different methods across epochs. The x-axis represents training epochs (from 1 to 200), and the stacked bars in each subplot represent the relative risks of three tasks in NYUv2 dataset: ‘Normal’, ‘Seg.’, and ‘Depth’. The top row shows unscaled risks, while the bottom row shows risks after applying the scaling method of each algorithm. The figure demonstrates that GO4Align maintains more stable risk ratios compared to other methods (UW, MGDA, NashMTL, and FAMO), indicating better alignment and balance between tasks during the training process. This stability suggests GO4Align’s effectiveness in mitigating task imbalance.
read the caption
Figure 8: Analysis on risk ratios. Compared with other works, the proposed GO4Align shows more stable ratios among tasks over epochs, indicating that GO4Align can maintain better alignment throughout the training process.
More on tables
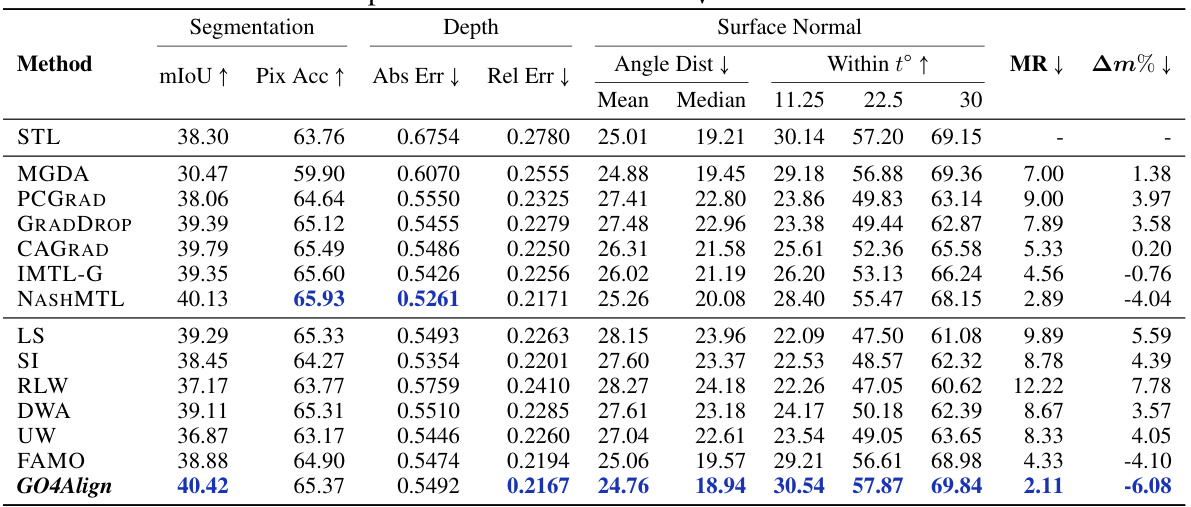
🔼 This table presents the results of the proposed GO4Align method and several baseline methods on the NYUv2 dataset. It compares gradient-oriented and loss-oriented multi-task optimization methods across three tasks: segmentation, depth, and surface normal. Metrics include mIoU, pixel accuracy, absolute and relative error for depth, angle distance and within-t for surface normal, mean rank (MR), and average performance drop (Am%). Lower values are better for error metrics, and lower values for MR and Am% indicate better overall multi-task learning performance.
read the caption
Table 1: Results on NYUv2 (3 tasks). The upper and lower tables categorize baseline methods into gradient-oriented and loss-oriented types, respectively. Each experiment is repeated over 3 random seeds, and the mean is reported. The best average result is marked in bold. MR and Am% are the main metrics for overall MTL performance. Metrics with↓ denote that the lower the better.
🔼 This table presents the performance comparison of various multi-task learning methods on the NYUv2 dataset, which consists of three tasks: segmentation, depth, and surface normal. The methods are categorized into gradient-oriented and loss-oriented approaches. The table reports several metrics (mIoU, PixAcc, AbsErr, RelErr, AngleDist, Mean, Median, Within t°, MR, Am%) to evaluate the performance of each method, with lower values generally indicating better performance. The best-performing method for each metric is highlighted in bold.
read the caption
Table 1: Results on NYUv2 (3 tasks). The upper and lower tables categorize baseline methods into gradient-oriented and loss-oriented types, respectively. Each experiment is repeated over 3 random seeds, and the mean is reported. The best average result is marked in bold. MR and Am% are the main metrics for overall MTL performance. Metrics with↓ denote that the lower the better.

🔼 This table presents the results of the NYUv2 experiment with 3 tasks. It compares various multi-task optimization (MTO) methods, categorized as gradient-oriented and loss-oriented. The table shows performance metrics (mIoU, PixAcc, AbsErr, RelErr, AngleDist, Mean, Median, Within t°, MR, and Am%) for each method, averaged over three random seeds. Lower values are better for most metrics. The best average performance across all metrics is highlighted in bold.
read the caption
Table 1: Results on NYUv2 (3 tasks). The upper and lower tables categorize baseline methods into gradient-oriented and loss-oriented types, respectively. Each experiment is repeated over 3 random seeds, and the mean is reported. The best average result is marked in bold. MR and Am% are the main metrics for overall MTL performance. Metrics with↓ denote that the lower the better.
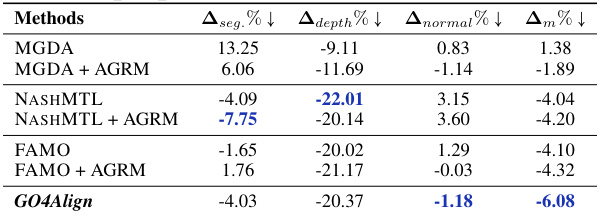
🔼 This table presents the ablation study results comparing different multi-task optimization (MTO) methods with and without the adaptive group risk minimization (AGRM) principle proposed in the paper. It shows the performance improvement achieved by integrating AGRM with existing MTO methods on the NYUv2 dataset. The metrics seg.%, depth%, and normal% represent the average performance drop relative to single-task learning (STL) for the segmentation, depth, and normal tasks, respectively. Am% represents the overall average performance drop across all three tasks. The results demonstrate that AGRM consistently improves performance.
read the caption
Table 4: Comparisons of existing MTO methods with the proposed AGRM on NYUv2.

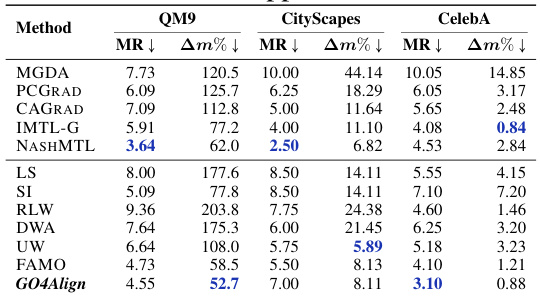
🔼 This table presents the results of the proposed GO4Align method and several baseline methods on the NYUv2 dataset, which involves three tasks. The table is split into two sections: gradient-oriented and loss-oriented methods. For each method, various metrics are reported, including mIoU, Pixel Accuracy, Absolute Error, Relative Error, Angle Distance, Mean, Median, Within t°, MR, and Am%. The best average result for each metric is highlighted in bold. Lower values are generally preferred for the metrics that include the symbol ↓.
read the caption
Table 1: Results on NYUv2 (3 tasks). The upper and lower tables categorize baseline methods into gradient-oriented and loss-oriented types, respectively. Each experiment is repeated over 3 random seeds, and the mean is reported. The best average result is marked in bold. MR and Am% are the main metrics for overall MTL performance. Metrics with↓ denote that the lower the better.

🔼 This table presents the results of the experiments conducted on the NYUv2 dataset, which involves three tasks. It compares various multi-task learning (MTL) methods, categorized into gradient-oriented and loss-oriented approaches. The table shows multiple evaluation metrics, including mean Intersection over Union (mIoU), pixel accuracy, absolute and relative error, angle distance, and the mean rank (MR) and average performance drop (Am%). Lower values are better for most metrics. The best-performing method for each metric is highlighted in bold.
read the caption
Table 1: Results on NYUv2 (3 tasks). The upper and lower tables categorize baseline methods into gradient-oriented and loss-oriented types, respectively. Each experiment is repeated over 3 random seeds, and the mean is reported. The best average result is marked in bold. MR and Am% are the main metrics for overall MTL performance. Metrics with↓ denote that the lower the better.
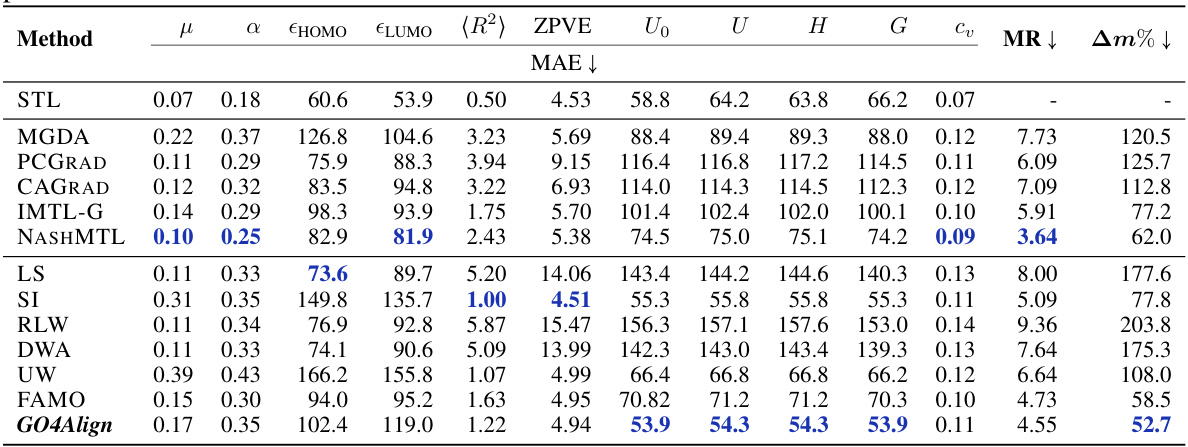
🔼 This table presents the results of the proposed GO4Align method and several baseline methods on the NYUv2 dataset. It compares the performance of gradient-oriented and loss-oriented multi-task optimization methods across three tasks (segmentation, depth, and surface normal). The metrics used to evaluate performance include mean Intersection over Union (mIoU), pixel accuracy (Pix Acc), absolute error (Abs Err), relative error (Rel Err), angle distance (Angle Dist), and two overall multi-task learning (MTL) metrics: mean rank (MR) and average performance drop (Am%). Lower values are generally better for most metrics. The best-performing method for each metric is highlighted in bold.
read the caption
Table 1: Results on NYUv2 (3 tasks). The upper and lower tables categorize baseline methods into gradient-oriented and loss-oriented types, respectively. Each experiment is repeated over 3 random seeds, and the mean is reported. The best average result is marked in bold. MR and Am% are the main metrics for overall MTL performance. Metrics with↓ denote that the lower the better.
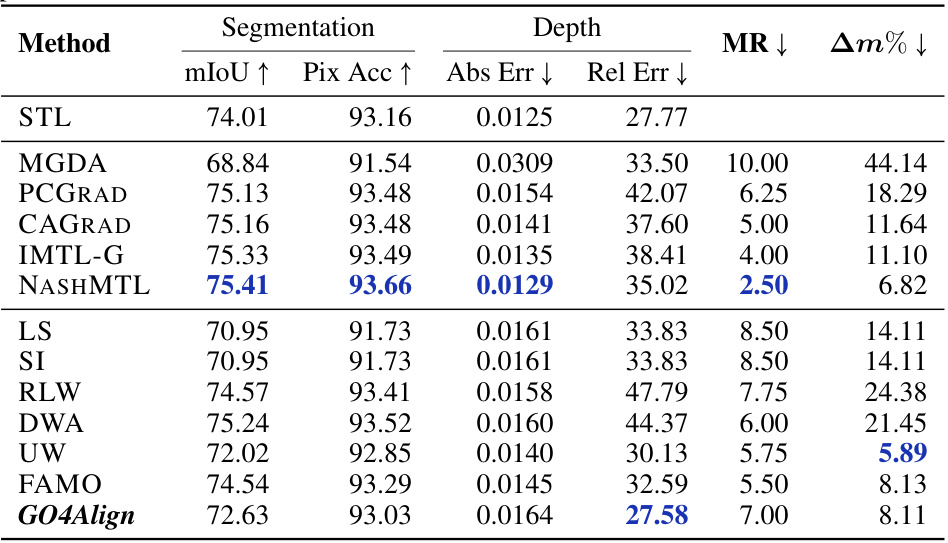
🔼 This table presents the results of the proposed GO4Align method and various baseline methods on the NYUv2 dataset, which involves three tasks: segmentation, depth prediction, and surface normal prediction. The table is split into two parts: one for gradient-oriented methods and one for loss-oriented methods. Each method’s performance is evaluated using several metrics (mIoU, Pix Acc, Abs Err, Rel Err, Angle Dist, Within t°, MR, Am%), with lower values indicating better performance for most metrics. The best average results for each metric are highlighted in bold.
read the caption
Table 1: Results on NYUv2 (3 tasks). The upper and lower tables categorize baseline methods into gradient-oriented and loss-oriented types, respectively. Each experiment is repeated over 3 random seeds, and the mean is reported. The best average result is marked in bold. MR and Am% are the main metrics for overall MTL performance. Metrics with ↓ denote that the lower the better.
🔼 This table presents the results of the proposed GO4Align method and various baseline methods on the NYUv2 dataset, which involves three tasks: image segmentation, depth prediction, and surface normal prediction. The table categorizes baseline methods into gradient-oriented and loss-oriented approaches. For each method, it shows multiple metrics such as mIoU, pixel accuracy, absolute error, relative error, and angle distance. The best average result for each metric is highlighted in bold. Finally, the table also shows two main metrics, MR (average rank) and Am% (average relative performance drop), to assess the overall performance of multi-task learning, with lower values indicating better performance. The table shows GO4Align outperforms other methods.
read the caption
Table 1: Results on NYUv2 (3 tasks). The upper and lower tables categorize baseline methods into gradient-oriented and loss-oriented types, respectively. Each experiment is repeated over 3 random seeds, and the mean is reported. The best average result is marked in bold. MR and Am% are the main metrics for overall MTL performance. Metrics with↓ denote that the lower the better.
Full paper#