TL;DR#
Classical Multidimensional Scaling (MDS) struggles with non-Euclidean distance matrices, often discarding valuable information from negative eigenvalues. This limitation hinders accurate dimension reduction in applications dealing with complex data like graph networks or those arising from physics models, where non-Euclidean geometries are common. Previous attempts to improve upon classical MDS haven’t fully addressed these core issues, resulting in suboptimal solutions and a ‘dimensionality paradox’ where increasing dimensions can worsen results.
This research introduces Non-Euclidean MDS (Neuc-MDS), a novel approach that overcomes these limitations. Neuc-MDS cleverly generalizes the inner product to symmetric bilinear forms, effectively utilizing both positive and negative eigenvalues of the dissimilarity Gram matrix. Through rigorous error analysis and optimal algorithms, Neuc-MDS significantly reduces STRESS (sum of squared error) and avoids the dimensionality paradox. The method’s effectiveness is demonstrated through extensive experiments on synthetic and real-world datasets, showing substantial improvements over classical MDS and other state-of-the-art techniques.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the limitations of classical MDS in handling non-Euclidean data, a prevalent issue in many fields. By offering a novel, theoretically-sound method, it enables more accurate and insightful dimension reduction for a wider range of datasets. This opens new avenues for research in graph embedding, AI for science, and other areas, promising significant advancements.
Visual Insights#
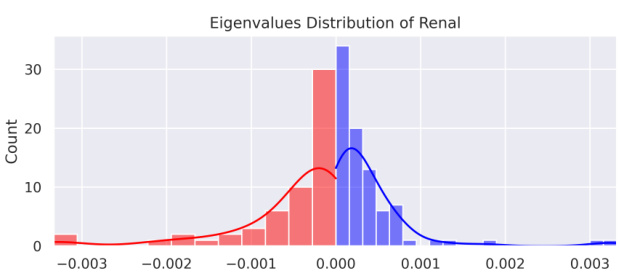
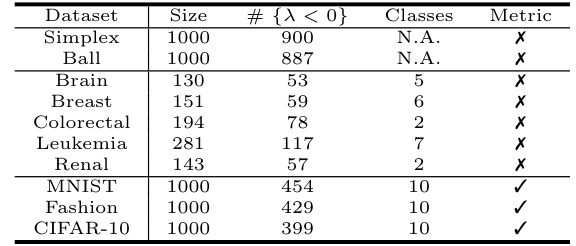
🔼 This figure shows the distribution of eigenvalues for the Renal dataset. The x-axis represents the eigenvalue values, and the y-axis represents the count of eigenvalues within each bin. The distribution is bimodal, showing a significant number of both negative and positive eigenvalues. The red bars represent negative eigenvalues, while the blue bars represent positive eigenvalues. This bimodal distribution highlights the non-Euclidean nature of the data, as Euclidean data would primarily exhibit positive eigenvalues.
read the caption
Figure 1: Negative (red), positive (blue). Eigenvalues Distribution of Renal

🔼 This table presents the STRESS values achieved by different multidimensional scaling methods (CMDS, Lower-MDS, Neuc-MDS, Neuc-MDS+, and SMACOF) on various datasets (Random-Simplex, Euclidean Ball, Brain, Breast, Colorectal, Leukemia, Renal, MNIST, Fashion-MNIST, and CIFAR-10). Lower STRESS indicates better performance. The results show that Neuc-MDS and Neuc-MDS+ generally achieve significantly lower STRESS compared to the other methods.
read the caption
Table 2: Evaluation Results on STRESS.
In-depth insights#
Non-Euclidean MDS#
The concept of “Non-Euclidean MDS” extends classical Multidimensional Scaling (MDS) by addressing its limitations when dealing with non-Euclidean distance matrices. Classical MDS assumes Euclidean geometry, which restricts its applicability to datasets where distances conform to the properties of Euclidean space. Non-Euclidean MDS generalizes the underlying geometric assumptions, enabling the analysis of datasets exhibiting dissimilarities that violate the triangle inequality or include negative values. This generalization is achieved by replacing the standard inner product with symmetric bilinear forms, allowing the algorithm to leverage both positive and negative eigenvalues of the dissimilarity Gram matrix. This approach enhances the accuracy and interpretability of the results, effectively resolving the dimensionality paradox—a phenomenon where increasing the dimensionality in classical MDS can unexpectedly worsen the error. By incorporating the complete spectrum of eigenvalues, Non-Euclidean MDS provides a more robust and informative representation of complex relationships within the data.
Bilinear Form#
The concept of a bilinear form is central to the paper’s approach to non-Euclidean multidimensional scaling (MDS). Instead of relying on the standard Euclidean inner product, which assumes Euclidean geometry, the authors generalize to symmetric bilinear forms. This allows them to handle datasets with dissimilarities that are non-Euclidean and non-metric, including those with negative eigenvalues in their Gram matrix. By optimizing over the choice of bilinear forms (specifically, via eigenvalue selection), the method effectively captures the underlying geometry of the data, overcoming limitations of classical MDS which only considers positive eigenvalues and thus imposes a Euclidean structure inappropriately. The bilinear form allows for more flexibility in representing the relationships between data points, leading to potentially more accurate and insightful low-dimensional embeddings. The use of bilinear forms is a key innovation that provides a theoretically grounded extension of MDS to a broader class of datasets.
STRESS Error#
The concept of STRESS error is central to the paper’s evaluation of multidimensional scaling (MDS) techniques. STRESS, or the sum of squared differences between input dissimilarities and embedded distances, quantifies the accuracy of the embedding. The paper introduces non-Euclidean MDS (Neuc-MDS) to address limitations of classical MDS, particularly its suboptimal performance and the dimensionality paradox (STRESS increasing with added dimensions) when dealing with non-Euclidean data. A key contribution is the in-depth analysis of the STRESS error, decomposing it into three terms to gain a deeper understanding of its behavior. Neuc-MDS leverages this analysis to optimally select eigenvalues, not discarding the negative ones as classical MDS does, resulting in lower STRESS. The theoretical analysis examines the asymptotic behavior of STRESS for both classical and Neuc-MDS on random matrices, demonstrating Neuc-MDS’s superior performance in reducing the error, especially for high-dimensional embeddings. This theoretical analysis, along with extensive empirical evaluation on diverse datasets, ultimately validates the effectiveness of Neuc-MDS in achieving lower STRESS and resolving the dimensionality paradox.
Eigenvalue Selection#
The eigenvalue selection process is critical for the success of Non-Euclidean Multidimensional Scaling (Neuc-MDS). The core idea is to select a subset of eigenvalues from the dissimilarity matrix’s eigendecomposition to minimize the STRESS error, which quantifies the discrepancy between the input dissimilarities and the embedded distances. Optimal selection isn’t simply choosing the largest k eigenvalues, as classical MDS does. Instead, Neuc-MDS leverages both positive and negative eigenvalues. A key contribution is the development of an efficient algorithm to solve this eigenvalue selection problem, which is shown to be solvable in polynomial time, despite the NP-hard nature of general quadratic integer programming. The algorithm cleverly balances positive and negative eigenvalues to minimize the STRESS error’s lower bound. The theoretical analysis of the algorithm demonstrates its effectiveness in achieving a better approximation than classical MDS, especially for high-dimensional data, effectively resolving the dimensionality paradox of classical MDS. The approach moves beyond a binary selection to consider general linear combinations of eigenvalues, leading to an even more refined algorithm (Neuc-MDS+), achieving even lower STRESS errors in many cases.
Dimensionality Paradox#
The “Dimensionality Paradox” in classical Multidimensional Scaling (MDS) highlights a critical limitation: increasing the dimensionality of the embedding does not always lead to improved accuracy. In fact, STRESS, a common measure of embedding error, can paradoxically increase as more dimensions are added, especially when dealing with non-Euclidean data. This counterintuitive behavior stems from the inherent assumptions of Euclidean geometry within classical MDS, which are violated by non-Euclidean distances. Classical MDS attempts to force non-Euclidean data into an inappropriate Euclidean framework, leading to suboptimal and unstable solutions. The authors of the paper address this by proposing Neuc-MDS, which generalizes MDS to non-Euclidean spaces, enabling better handling of negative eigenvalues and ultimately resolving the paradox. Neuc-MDS leverages symmetric bilinear forms, providing a more robust embedding that avoids the pitfalls of the Euclidean constraints and achieves lower STRESS even with higher dimensionality.
More visual insights#
More on figures
🔼 The figure shows the STRESS values for four different methods (Neuc-MDS, Neuc-MDS+, cMDS, and Lower-MDS) across different target dimensions. It illustrates that Neuc-MDS and Neuc-MDS+ consistently achieve lower STRESS values compared to the other two methods, especially as the target dimension increases. This addresses the ‘dimensionality paradox’ observed in classical MDS, where increasing the dimensionality may lead to increased STRESS.
read the caption
Figure 2: Neuc-MDS and Neuc-MDS+ consistently produce lower STRESS on all dimensions.

🔼 The figure shows the STRESS (sum of squared pairwise error) for different dimensionality reduction methods (Neuc-MDS, Neuc-MDS+, cMDS, Lower-MDS) on two datasets (Random-simplex, Renal). It demonstrates that Neuc-MDS and Neuc-MDS+ consistently achieve lower STRESS across different dimensionality choices (k) compared to the other methods. The plot highlights the dimensionality paradox of cMDS where increasing dimensionality does not always reduce STRESS, whereas Neuc-MDS and Neuc-MDS+ show consistent improvement.
read the caption
Figure 2: Neuc-MDS and Neuc-MDS+ consistently produce lower STRESS on all dimensions.

🔼 This figure shows the STRESS error for different dimension reduction methods (Neuc-MDS, Neuc-MDS+, classical MDS, and Lower-MDS) applied to two datasets, Random-simplex and Renal. It demonstrates that Neuc-MDS and Neuc-MDS+ consistently achieve lower STRESS than the other methods across various dimensions. The plot for Lower-MDS is shorter because its target dimension k is limited by the number of positive eigenvalues, unlike Neuc-MDS and Neuc-MDS+. This figure visually highlights the advantage of Neuc-MDS and Neuc-MDS+ in addressing the dimensionality paradox, where increasing the dimension in classical MDS can sometimes lead to higher STRESS.
read the caption
Figure 2: Neuc-MDS and Neuc-MDS+ consistently produce lower STRESS on all dimensions.
More on tables
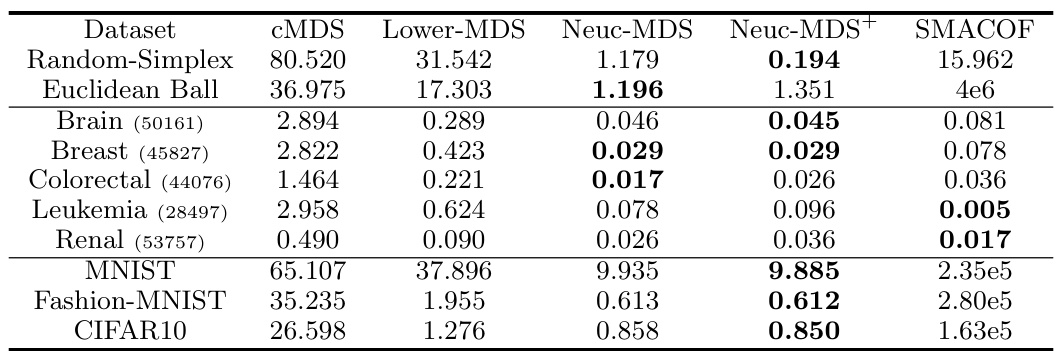
🔼 The table compares the STRESS (sum of squared error) of different multidimensional scaling methods (CMDS, Lower-MDS, Neuc-MDS, Neuc-MDS+, SMACOF) across various datasets (synthetic and real-world). Lower STRESS values indicate better performance.
read the caption
Table 2: Evaluation Results on STRESS.

🔼 This table presents the average geometric distortion for different methods (cMDS, Lower-MDS, Neuc-MDS, and Neuc-MDS+) across ten diverse datasets. Average geometric distortion is a metric measuring the multiplicative error between the input dissimilarities and the computed distances in the embedded low-dimensional space. Lower values indicate better performance. The datasets include synthetic datasets (Random-Simplex, Euclidean Ball) and real-world datasets (genomics data from CuMiDa and image datasets MNIST, Fashion-MNIST, CIFAR-10).
read the caption
Table 3: Evaluation Results on Average Geometric Distortion.
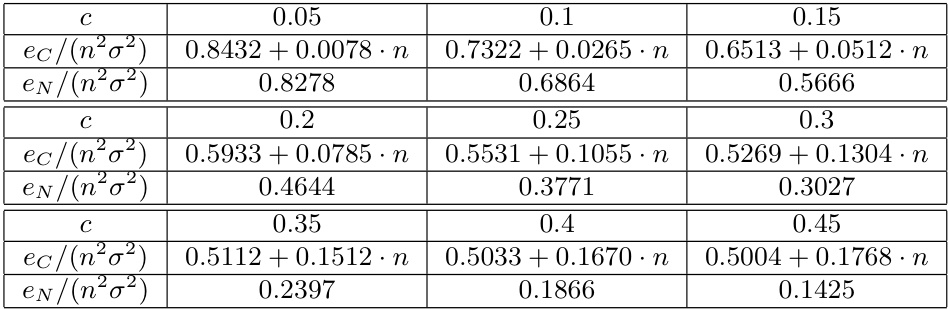
🔼 This table presents the results of the error analysis for classical MDS (ec) and Neuc-MDS (eN) on random symmetric matrices. The error terms are normalized by dividing n²σ², where n is the dimension of the matrix and σ² is the variance of the matrix elements. The values are shown for different choices of c, which represents the ratio k/n, where k is the number of selected eigenvalues and n is the total number of eigenvalues. The table illustrates the impact of the ratio of selected eigenvalues (k) to total number of eigenvalues (n) on the error of classical MDS and Neuc-MDS.
read the caption
Table 4: This table shows the error terms ec and en of different choices of c∈ (0,0.5) with c = k/n, normalized by dividing n²σ².

🔼 This table shows the results of the error term eN, which is normalized by dividing n²σ², for different choices of c, where c ranges from 0.5 to 0.95. The values demonstrate how eN decreases as c approaches 1, illustrating the impact of the chosen dimension (k) relative to the total dimension (n) on the error in non-Euclidean multidimensional scaling.
read the caption
Table 5: This table shows the error term eN of different choices of c ∈ [0.5, 1) with c = k/n, normalized by dividing n²σ².
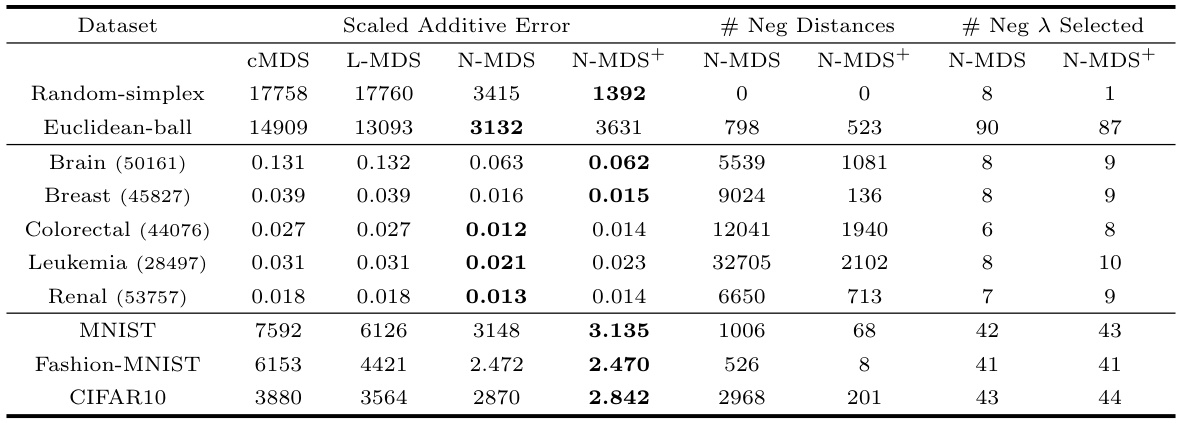
🔼 This table presents the performance comparison of four multidimensional scaling algorithms, namely Lower-MDS, Neuc-MDS, Neuc-MDS+, and cMDS, across ten diverse datasets. The comparison is based on three metrics: scaled additive error, number of negative distances, and the number of negative eigenvalues selected. Lower error values indicate better performance.
read the caption
Table 6: Original Evaluation Results on All Datasets for Lower-MDS (L-MDS), Neuc-MDS (N-MDS) and Neuc-MDS+ (N-MDS+). Metrics include scaled additive error, number of negative distances and number of negative eigenvalues selected.

🔼 This table presents the STRESS values resulting from different multidimensional scaling methods (CMDS, Lower-MDS, Neuc-MDS, Neuc-MDS+, and SMACOF) applied to various datasets. Lower STRESS values indicate better performance in accurately representing the input dissimilarities in a lower-dimensional space. The datasets include synthetic data (Random-Simplex, Euclidean Ball) and real-world data (Brain, Breast, Colorectal, Leukemia, Renal, MNIST, Fashion-MNIST, CIFAR-10).
read the caption
Table 2: Evaluation Results on STRESS.
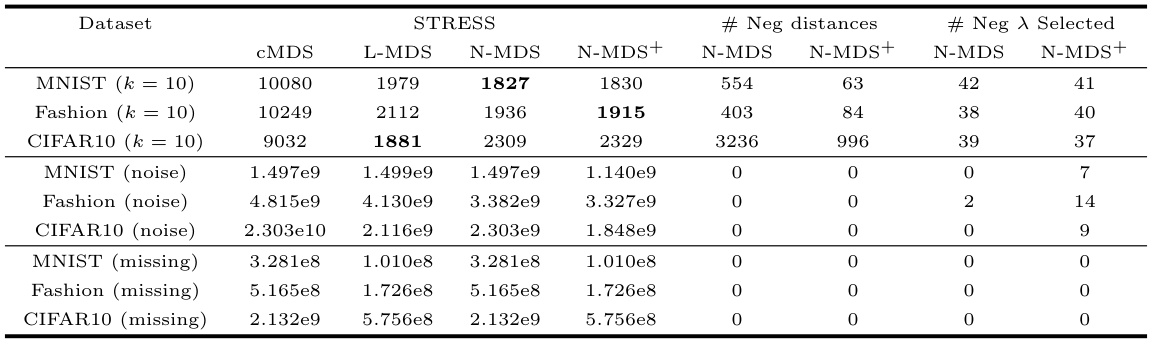
🔼 This table presents the results of experiments on image datasets using different perturbation methods. It shows the STRESS values, the number of negative distances, and the number of negative eigenvalues selected for CMDS, L-MDS, Neuc-MDS, and Neuc-MDS+. The perturbation methods used are adding Gaussian noise to distances, randomly removing data entries from coordinates, and increasing the number of nearest neighbors in k-NN.
read the caption
Table 8: Evaluation Results on Image Datasets with other perturbation metrics.
Full paper#



















