TL;DR#
Many real-world applications involve selecting specific subsets from a larger dataset before performing multiple hypothesis testing. This often leads to issues with controlling the False Discovery Rate (FDR) because standard methods don’t account for the selection process. This paper addresses this challenge by proposing a method that accurately captures the distorted distribution of test statistics after selection and successfully controls the FDR.
The researchers achieve this by leveraging a holdout labeled dataset to construct valid test statistics. They propose an adaptive strategy for picking labeled data based on the stability of the selection rule. This method, combined with the Benjamini-Hochberg (BH) procedure, controls FDR over the selected subset. A unified theoretical framework ensures the method’s validity even with the randomness of the selected subset and the dependence among the test statistics.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on multiple hypothesis testing and selective inference. It provides a novel framework for controlling the false discovery rate (FDR) after data-dependent selection, addressing a critical limitation in existing methods. The unified theoretical framework is applicable in various complex scenarios. This work opens new avenues for improving the accuracy and reliability of multiple testing in complex settings, particularly in machine learning and predictive modeling where data-dependent selection is common.
Visual Insights#

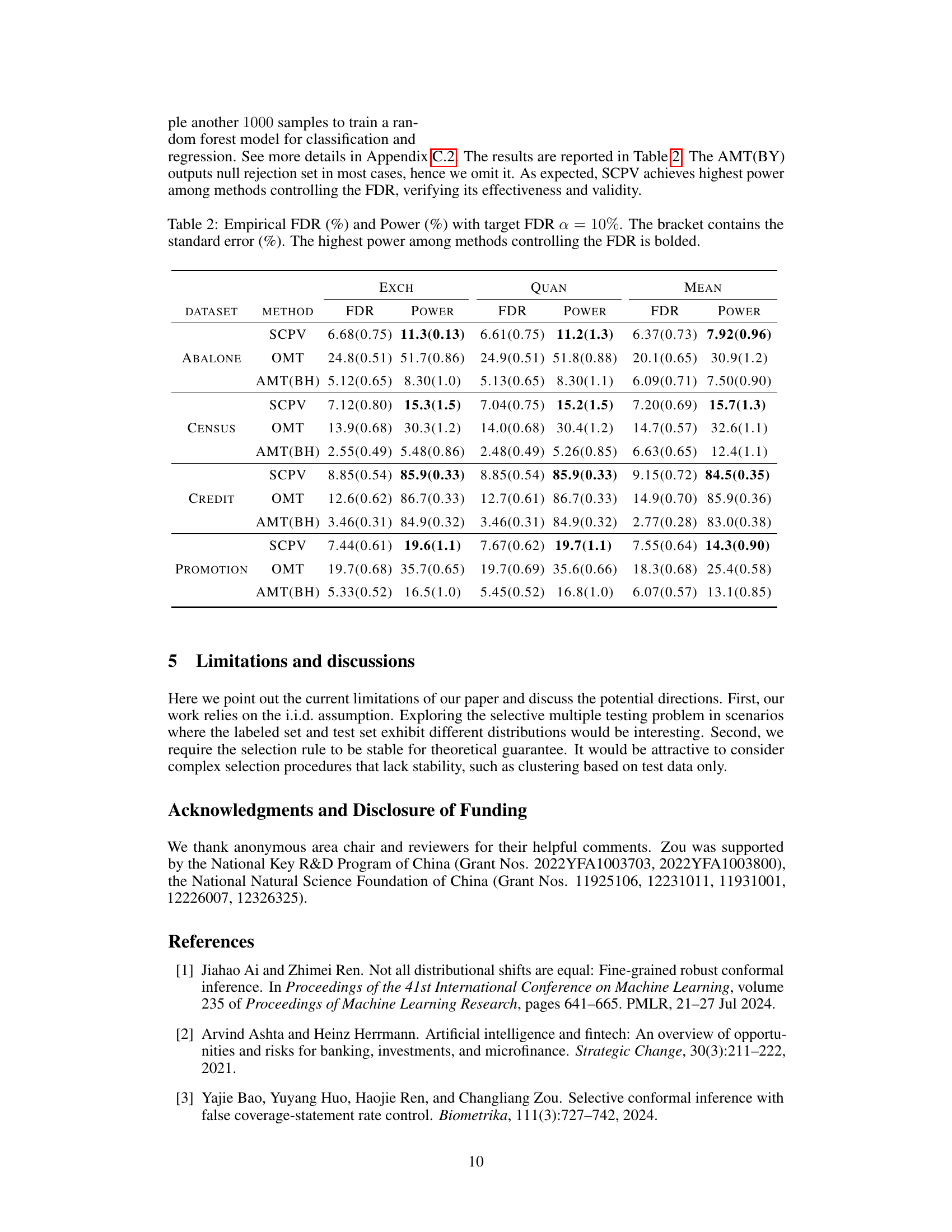
🔼 This figure displays the empirical False Discovery Rate (FDR) and statistical power of five different multiple testing methods across two distinct data-generating scenarios (Case A and Case B) and three selection rule types (Exchangeable, Quantile, and Mean). The x-axis represents the noise strength in the data, and the y-axis represents either FDR or power. The black dashed line in the FDR plots indicates the target FDR level of 10%. The figure showcases the performance of the proposed Selective Conformal P-value (SCPV) method in comparison to other benchmark methods (Ordinary Multiple Testing, Adjusted Multiple Testing with Benjamini-Hochberg and Benjamini-Yekutieli procedures, and Selection Conditional Conformal Prediction).
read the caption
Figure 1: Empirical FDR (left) and Power (right) of five methods under different scenarios and selection rules. The Noise Strength varies from 0.1 to 1. The black dashed line in the left plot denotes the target FDR level a = 10%.

🔼 This table summarizes the characteristics of four real-world datasets used in the paper’s experiments to evaluate the proposed selective conformal p-value method. For each dataset, it lists the number of features, the number of instances (data points), and whether the task is regression (Reg) or classification (Cla). These datasets represent diverse scenarios and data sizes to test the robustness and generalizability of the method.
read the caption
Table 1: Summary of real-world datasets for conformalized multiple testing
In-depth insights#
Selective Conformal#
Selective conformal methods aim to address the challenges of applying conformal prediction techniques to datasets where a selection process has already been applied. This selection, often data-dependent, distorts the distribution of the data, impacting the validity of standard conformal inference. The core idea is to create a calibration set that reflects the distribution of the selected data, mitigating the bias introduced by the prior selection. This might involve using a holdout set or adaptively selecting data from a labeled set based on the stability of the selection process to ensure exchangeability between calibration and test data. This sophisticated approach enables the construction of valid p-values, even after data-dependent selection, preserving the crucial property of conformal inference while applying multiple testing procedures. This addresses the critical problem of selective inference, ensuring the integrity of results when dealing with subsets of data chosen non-randomly. A key aspect of this research is developing a theoretical framework and algorithms for various selection rules, enhancing the robustness and reliability of conformalized multiple testing in realistic scenarios.
Adaptive Calibration#
Adaptive calibration, in the context of selective conformal inference, addresses the challenge of maintaining valid p-values after a data-dependent selection process. Standard conformal methods assume exchangeability between calibration and test sets, an assumption violated by selection. Adaptive calibration dynamically adjusts the calibration set based on the stability of the selection rule, aiming to re-establish exchangeability between the chosen calibration subset and the selected test data. This is crucial for ensuring that the resulting p-values accurately reflect uncertainty, leading to valid FDR control. The adaptive nature allows the method to handle a wider range of selection procedures, including those with varying levels of stability, and to improve the efficiency and power of the approach in more complex scenarios. The key insight is the balance between preserving the validity of the inference and maintaining sufficient power to detect signals of interest.
FDR Control#
The research paper focuses on controlling the False Discovery Rate (FDR) in the context of conformalized multiple testing, particularly after data-dependent selection. A key challenge addressed is the distortion of the test statistic distribution caused by the selection process. The authors propose using a holdout labeled dataset to construct valid conformal p-values, which accurately reflect the distribution of the selected test units. Their approach involves adaptively choosing data for calibration based on the selection rule’s stability, ensuring exchangeability between calibration and test data. Implementing the Benjamini-Hochberg (BH) procedure, they demonstrate theoretical FDR control under specific selection rules (joint-exchangeable and top-K), extending to a weaker stability condition via an adaptive strategy. The effectiveness and validity are empirically validated across diverse scenarios, highlighting the method’s resilience and improved power compared to existing alternatives.
Stability Analysis#
A stability analysis in the context of a machine learning model assesses how robust its performance is to various perturbations. In the case of selective conformal inference, stability is crucial because the selection process introduces randomness into the model’s input. A stable selection rule produces consistent results even when small changes are made to the data. The analysis would delve into how the choice of selection criteria, data-dependent thresholding methods, and specific algorithms used impact the overall stability. Evaluating stability often involves metrics that measure the consistency of the selected subset across various iterations of the selection process. Theoretical guarantees of stability are desirable, especially when dealing with specific classes of selection rules. The goal is to determine conditions that ensure the FDR control holds under perturbations, demonstrating the reliability and applicability of the conformalized multiple testing procedure in diverse settings. The analysis might also investigate the relationship between selection stability and the power of the test, examining whether more stable selections lead to a greater number of true discoveries while maintaining the FDR control.
Future Extensions#
Future research directions stemming from this work could explore relaxing the strong stability assumptions on selection rules, thereby broadening applicability to more complex, real-world scenarios. Investigating alternative calibration set selection strategies beyond the adaptive approach presented would enhance robustness and efficiency. Exploring extensions to more general model settings beyond regression and classification, such as survival analysis or time series data, is crucial for practical impact. A key focus should be on developing more powerful and efficient multiple testing procedures that account for the complexities introduced by data-dependent selection. This could involve leveraging recent advances in selective inference or other theoretical frameworks. Finally, extensive empirical evaluation on diverse real-world datasets with various selection mechanisms would solidify the practical utility and limitations of the proposed methods.
More visual insights#
More on tables
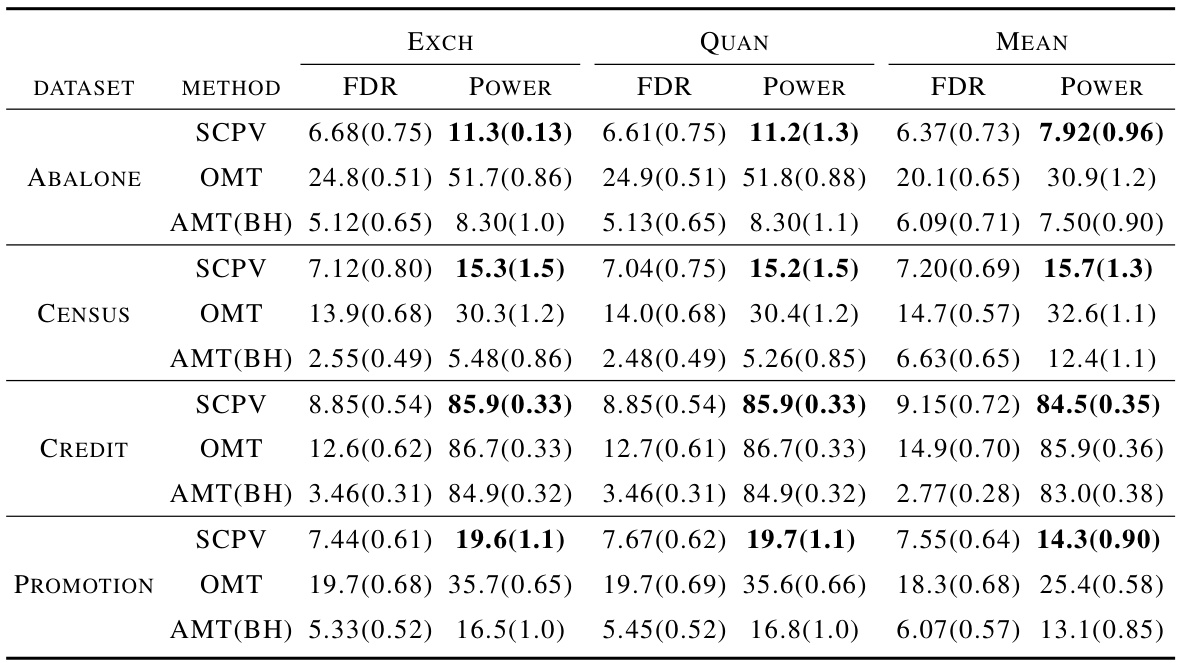
🔼 This table presents the empirical False Discovery Rate (FDR) and power of several methods for multiple testing after data-dependent selection. The methods compared are SCPV (the proposed method), OMT (ordinary multiple testing), and AMT (adjusted multiple testing) using both Benjamini-Hochberg (BH) and Benjamini-Yekutieli (BY) procedures. Results are shown for three different selection rules (Exchangeable, Quantile, and Mean) across four real-world datasets (Abalone, Census, Credit, and Promotion). The FDR is the expected proportion of false positives among rejected hypotheses, while power represents the proportion of correctly identified true positives among all true positives. The standard error is provided in parentheses for each metric.
read the caption
Table 2: Empirical FDR (%) and Power (%) with target FDR α = 10%. The bracket contains the standard error (%). The highest power among methods controlling the FDR is bolded.

🔼 This table presents the empirical False Discovery Rate (FDR) and power for three different methods (SCA, SCPV, and AMT) under two different data-generating scenarios (Case A and Case B) and two different selection rules (Quantile and Mean). The target FDR level is set at 10%, and the results are based on 500 repetitions. The table compares the performance of the proposed selective conformal p-value method (SCPV) against two benchmark methods: the self-consistent/compliant adjustment (SCA) method and a method using adjusted p-values (AMT). The results show the effectiveness of SCPV in controlling FDR while maintaining high power across different scenarios and selection rules.
read the caption
Table 3: Comparisons of empirical FDR (%) and Power (%) with target FDR level α = 10% by 500 repetitions.

🔼 This table compares the empirical FDR and power of InfoSCOP and SCPV methods under two different data-generating scenarios (Case A and Case B). The results show that both methods achieve close to the target FDR level of 10%, while SCPV shows slightly lower power. This comparison highlights the performance of the proposed SCPV method against an existing method with a similar objective (selective inference), demonstrating the effectiveness of the SCPV approach in controlling FDR under different scenarios.
read the caption
Table 4: Comparisons of empirical FDR (%) and Power (%) with target FDR level α = 10% by 500 repetitions.
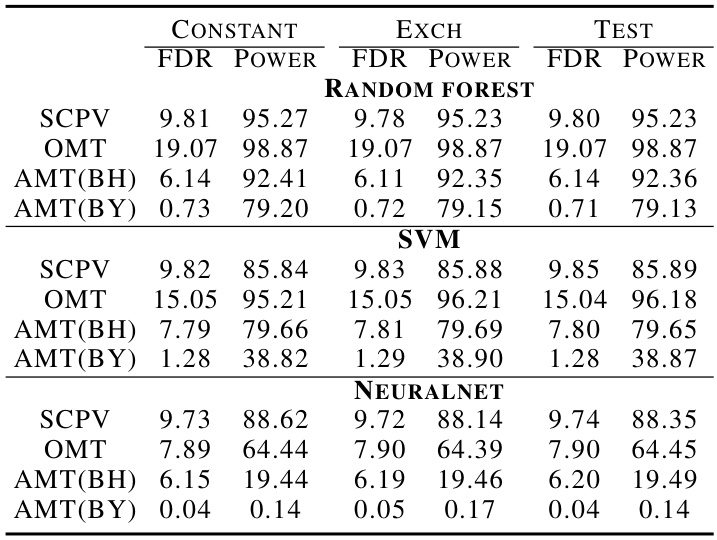
🔼 This table presents the empirical False Discovery Rate (FDR) and power of five different multiple testing methods under various scenarios and selection rules. The scenarios involve different data-generating processes and noise levels. The selection rules include exchangeable, quantile, and mean selection. The methods being compared are SCPV (the proposed method), OMT (ordinary multiple testing), AMT(BH) (adjusted multiple testing with Benjamini-Hochberg procedure), AMT(BY) (adjusted multiple testing with Benjamini-Yekutieli procedure), and SCOP (selection conditional conformal prediction). The results show the FDR and power for each method under each condition.
read the caption
Table 5: Comparisons of empirical FDR (%) and Power (%) under different scenarios and thresholds with target FDR α = 10% and noise strength σ = 0.5. The sample sizes of the labeled set and the test set are fixed as n = m = 1200.

🔼 This table presents the empirical False Discovery Rate (FDR) and power achieved by several multiple testing methods under different selection rules (Constant, Exch, Quan) in a diabetes prediction task using real-world data. The results show that the proposed SCPV method maintains FDR control while achieving higher power compared to other methods, especially in the Exch and Quan scenarios.
read the caption
Table 6: Comparisons of empirical FDR (%) and Power (%) with target FDR level α = 20% by 500 repetitions.

🔼 This table presents the results of empirical FDR and power for two groups obtained by K-means clustering, with a target FDR level of 20%. The results are based on 500 repetitions and compare the performance of SCPV, OMT, AMT(BH), and AMT(BY) methods. Group A and Group B represent two distinct clusters. The results show the FDR and Power for each method within each group.
read the caption
Table 7: Comparisons of empirical FDR (%) and Power (%) with target FDR level α = 20% by 500 repetitions.

🔼 This table presents the empirical False Discovery Rate (FDR) and power of five different multiple testing methods across three selection rules (Constant, Exch, Quan) in a breast cancer detection scenario using deep learning. The target FDR level is set at 10%, and 100 repetitions were performed for each configuration. The methods compared include the proposed Selective Conformal P-value (SCPV) method along with Ordinary Multiple Testing (OMT), and two adjusted multiple testing methods (AMT(BH) and AMT(BY)). The results show that SCPV effectively controls the FDR while maintaining reasonable power, outperforming the other methods.
read the caption
Table 8: Comparisons of empirical FDR (%) and Power (%) with target FDR level α = 10% by 100 repetitions.
Full paper#