Globally Convergent Variational Inference

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it offers the first global convergence result for variational inference (VI), a widely used but often problematic method in machine learning. This addresses a major limitation of existing VI techniques, which only guarantee convergence to local optima. The findings open new avenues for improving VI’s efficiency and reliability, potentially impacting various applications in machine learning and related fields.

Visual Insights

#

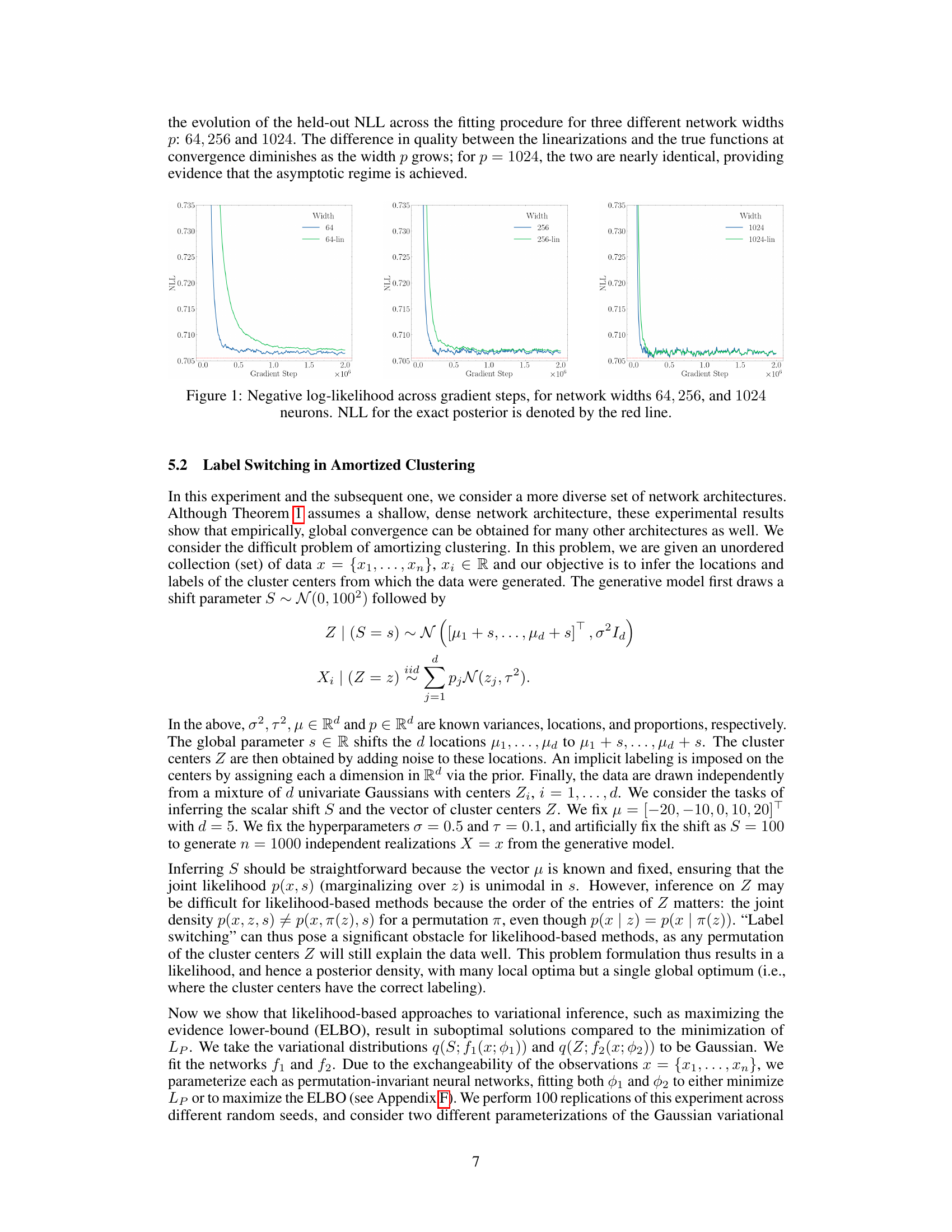
🔼 This figure shows the negative log-likelihood (NLL) across gradient descent steps for three different network widths (64, 256, and 1024 neurons). The NLL measures how well the model approximates the true posterior distribution. Lower NLL indicates better approximation. The figure compares the performance of the full neural network and its linearization around initialization, demonstrating that with increasing width, the linearized model closely approximates the full model’s performance, suggesting convergence to an asymptotic regime.

read the caption

Figure 1: Negative log-likelihood across gradient steps, for network widths 64, 256, and 1024 neurons. NLL for the exact posterior is denoted by the red line.

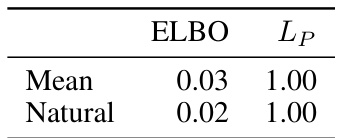
🔼 This table shows the proportion of times (out of 100 independent experimental replicates) that the estimated posterior mode for Z, obtained from the amortized clustering experiments, had its entries correctly ordered using either the ELBO or Lp objective. The ELBO approach is shown to exhibit label switching, where the entries of Z appear in different order across replicates.

read the caption

Table 1: Proportion out of one hundred replicates where posterior mode of q(Z; f2(x; $2)) was a vector in increasing order.

In-depth insights

#

Global VI Convergence

#

The concept of “Global VI Convergence” signifies a significant advancement in variational inference (VI). Traditional VI methods, using the evidence lower bound (ELBO), often suffer from convergence to suboptimal local optima, hindering their effectiveness. This research explores a novel approach that achieves global convergence, guaranteeing convergence to the true global optimum under specific conditions. This is achieved by minimizing the expected forward KL divergence instead of the ELBO. The key innovation involves leveraging the neural tangent kernel (NTK) framework to analyze gradient dynamics in function space. The NTK analysis helps establish a unique global solution and proves convergence to this solution under the asymptotic regime of infinite width networks. While the theoretical results hold for specific network architectures and conditions, the experimental validation demonstrates promising generalization, even in scenarios with finite-width networks and relaxed conditions. This breakthrough addresses the long-standing challenge of local optima in VI opening up opportunities for broader applications and more reliable inference across diverse tasks.

Forward KL Analysis

#

Forward KL divergence, unlike the commonly used ELBO in variational inference, offers a unique perspective by minimizing the expected KL divergence between the true posterior and the variational approximation. This approach, analyzed in the context of neural networks, presents several advantages. Firstly, it provides a direct measure of the discrepancy between the learned and true posteriors, unlike the ELBO which only provides a lower bound. Secondly, minimizing the forward KL can lead to better approximations of the posterior, particularly when dealing with complex, multimodal distributions. The analysis often involves studying the gradient dynamics in function space, sometimes using the neural tangent kernel (NTK) to characterize these dynamics, particularly in the asymptotic regime of infinitely wide networks. This functional approach helps to establish global convergence guarantees, which is a significant advantage over ELBO-based methods that often suffer from local optima. However, this approach usually requires strong assumptions (e.g., positive definiteness of the NTK), making the practical applicability dependent on the model and network architecture chosen. Further research needs to focus on relaxing these assumptions to improve the applicability and robustness of this promising technique.

NTK and Global Optima

#

The Neural Tangent Kernel (NTK) plays a crucial role in establishing global convergence results for variational inference. The NTK, in the infinite-width limit, essentially linearizes the neural network’s behavior, allowing for the analysis of gradient dynamics in function space. This linearization transforms the non-convex optimization problem into a convex one, under specific conditions such as the positive definiteness of the NTK. The core idea is that by leveraging the NTK’s properties, particularly its connection to reproducing kernel Hilbert spaces, the authors are able to demonstrate the existence of a unique global optimum for the variational objective. Consequently, gradient descent dynamics, analyzed through the lens of the NTK, are shown to converge to this unique global optimum.** However, it’s important to note that these results are asymptotic, holding strictly in the infinite-width limit. Finite-width networks, while exhibiting similar behavior in practice, do not offer the same theoretical guarantees. The authors provide experimental results to show that even in practice, the behavior aligns well with theoretical predictions, suggesting the potential for weaker conditions to achieve similar global convergence.

Amortized Inference

#

Amortized inference is a crucial technique in variational inference (VI) that significantly enhances efficiency by learning a single, shared function (encoder) to approximate the posterior distribution for all data points. This contrasts with non-amortized methods where a separate optimization process is needed for each data point. The key advantage is computational efficiency, especially when dealing with large datasets. The amortized approach learns a general mapping from the input data to the parameters of the approximate posterior, making inference much faster during test time. However, this efficiency comes at the cost of potential loss in accuracy. The shared encoder might not capture the nuances of the posterior for all data points equally well, resulting in an overall less precise approximation compared to non-amortized methods. Therefore, the choice between amortized and non-amortized inference involves a trade-off between computational efficiency and approximation accuracy. The effectiveness of amortized inference heavily relies on the expressiveness of the learned encoder. If the encoder is not sufficiently flexible, its capacity to model the diverse posterior distributions across different data points will be limited, resulting in poor performance. Neural networks are commonly employed as encoders in amortized inference due to their flexibility and capacity to learn complex mappings. This aspect of the method is crucial to its practical applicability and effectiveness. Further research should explore novel encoder architectures and training strategies to improve the performance of amortized inference and balance the trade-off with accuracy.

Limitations and Future

#

The research makes significant strides in establishing global convergence for variational inference, but several limitations exist. The theoretical results rely heavily on asymptotic analyses, particularly the infinite-width neural network assumption. The practical implications for finite-width networks, commonly used in practice, remain to be fully explored. The reliance on specific neural network architectures and activation functions also restricts the generalizability of the findings. Further research is needed to investigate the impact of different architectures, activation functions, and loss functions on the global convergence property. Addressing scenarios where the neural tangent kernel is not positive-definite or where the assumptions of strict convexity on the objective function are not fully satisfied, could broaden the applicability of the method. Future work should also focus on extending these results to more complex models and settings such as hierarchical models or those involving intractable likelihoods. Empirical evaluations on a wider range of tasks beyond the provided examples would further demonstrate the practical effectiveness and robustness of the proposed method. Exploring the trade-offs between global convergence and computational cost will also be crucial for real-world applications.

More visual insights

#

More on figures

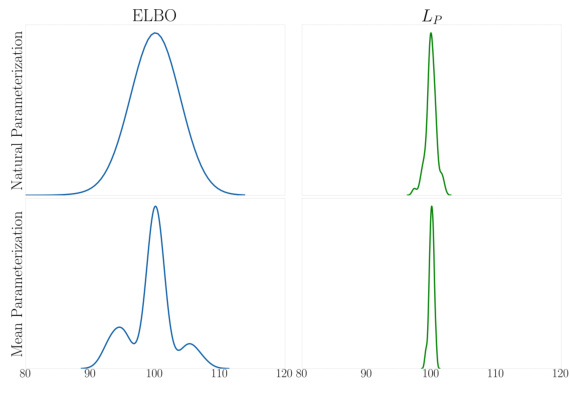
🔼 This figure displays kernel-smoothed frequency plots for the posterior mode estimates of the shift parameter S, obtained from 100 independent experimental replications, using both ELBO-based and Lp-based optimization methods. Two different parameterizations of the Gaussian variational distributions, mean-only and natural parameterization, are used for each method. The results illustrate that Lp-based optimization consistently recovers the correct value of S, while ELBO-based optimization exhibits label switching, converging to different permutations of the true cluster centers.

read the caption

Figure 2: Mode of q(S; f1(x; φ1)) across experimental replicates.

🔼 This figure shows 100 MNIST digits that have been rotated counterclockwise by 260 degrees. These digits were generated as part of a generative model used in the Rotated MNIST Digits experiment (Section 5.3) to test the ability of the expected forward KL divergence minimization approach to variational inference compared to likelihood-based methods for inferring a shared rotation angle for a set of MNIST digits.

read the caption

Figure 3: 100 of the N = 1000 data observations with counterclockwise rotation of θ = 260 degrees.

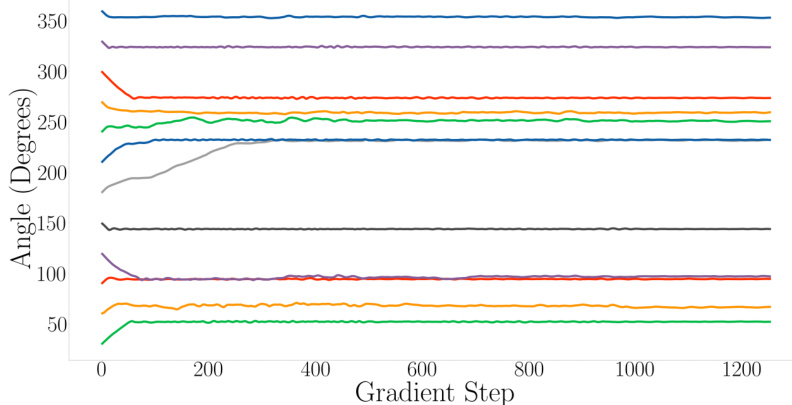
🔼 This figure shows the results of fitting a variational distribution to maximize the importance weighted bound (IWBO) for the rotated MNIST digits experiment. The IWBO is a likelihood-based approach that is prone to getting stuck in shallow local optima due to the multimodality of the likelihood in this particular problem. Different initializations of the rotation angle converge to different local optima. This is in contrast to the expected forward KL approach which consistently converges to the global optimum (shown in Figure 5).

read the caption

Figure 4: Estimate of angle θ across gradient steps, with fitting performed to maximize the IWBO.

🔼 This figure shows the negative log-likelihood (NLL) curves for three different network widths (64, 256, and 1024 neurons) during the training process. The NLL measures the quality of the variational posterior approximation to the true posterior distribution. Lower NLL values indicate better approximations. The red line represents the NLL of the exact posterior, serving as a baseline for comparison. As the network width increases, the NLL of the fitted network approaches the NLL of the exact posterior, demonstrating that wider networks perform better.

read the caption

Figure 1: Negative log-likelihood across gradient steps, for network widths 64, 256, and 1024 neurons. NLL for the exact posterior is denoted by the red line.

🔼 This figure shows the trajectories of the optimization of the expected forward KL divergence across multiple initializations. It zooms in on the first 2000 gradient steps to show the behavior of the optimization algorithm. The plot demonstrates that regardless of the starting point, the algorithm converges to the same solution. This illustrates that the algorithm is not trapped by local minima and consistently finds the global optimum.

read the caption

Figure 6: Zoomed-in trajectories across the first 2000 gradient steps, showing similar estimates regardless of initialization.

🔼 This figure compares the performance of minimizing the expected forward KL divergence against maximizing the evidence lower bound (ELBO) for variational inference on a simple rotated MNIST digit problem. The plot shows the forward and reverse KL divergences between the true posterior and the variational approximations obtained by both methods, along with the negative log-likelihood and the estimated angle. The results indicate that minimizing the expected forward KL leads to better approximations of the true posterior than maximizing the ELBO, which suffers from getting stuck in shallow local optima.

read the caption

Figure 7: Forward and reverse KL divergences to the true posterior across fitting for minimization of the expected forward KL (blue) or the negative ELBO (green). We also plot the negative log likelihood of the true angle, as well as the variational mode (true angle θtrue is plotted in red.)

Full paper

#