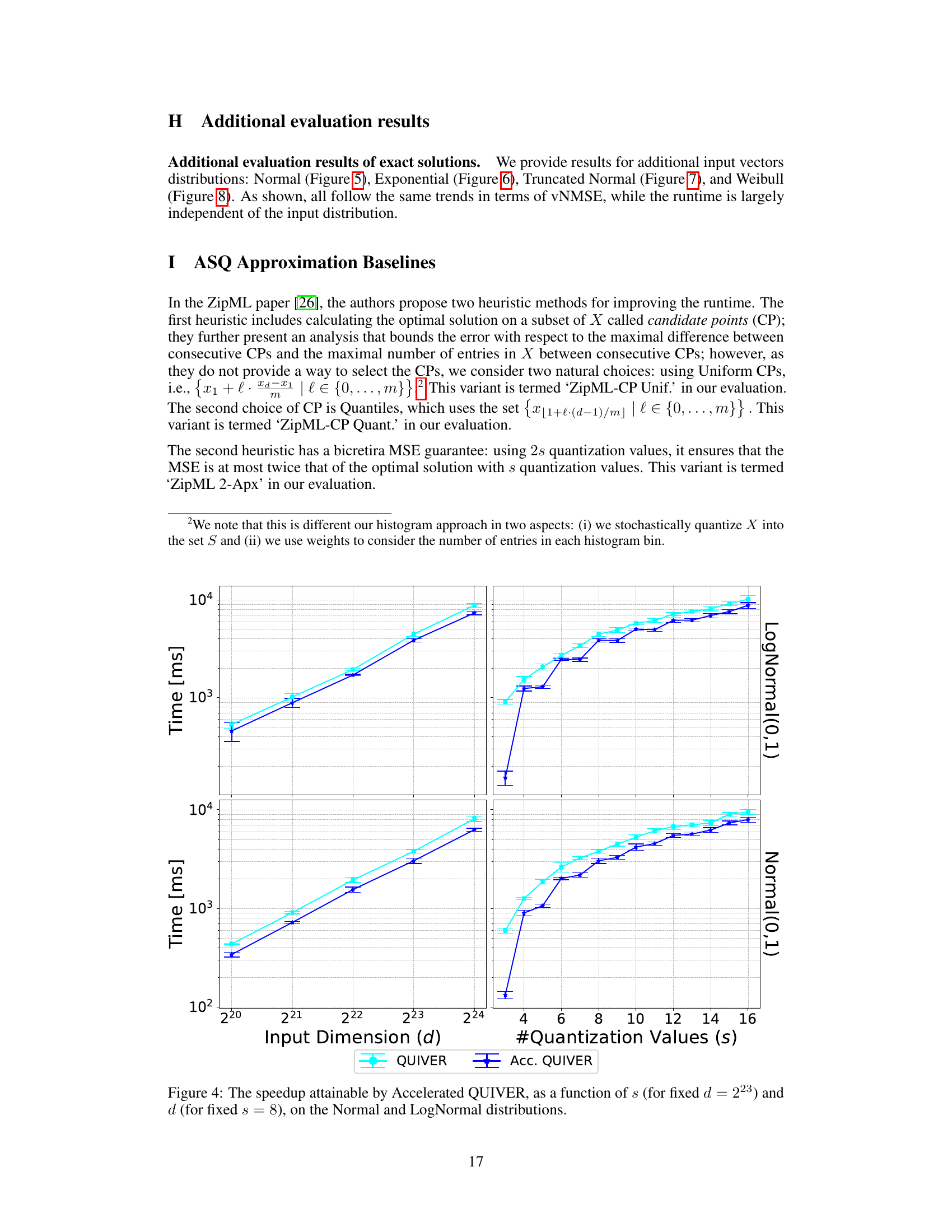
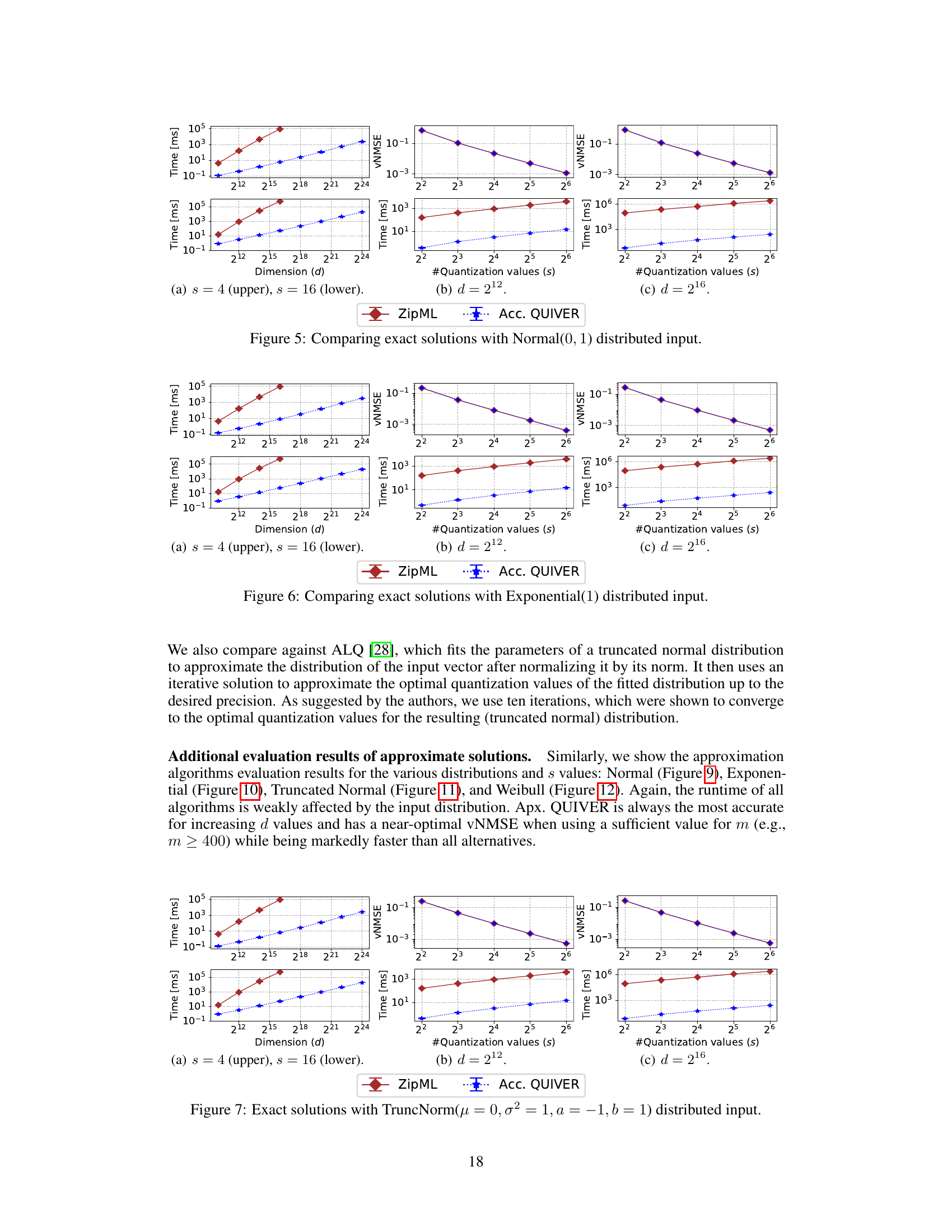
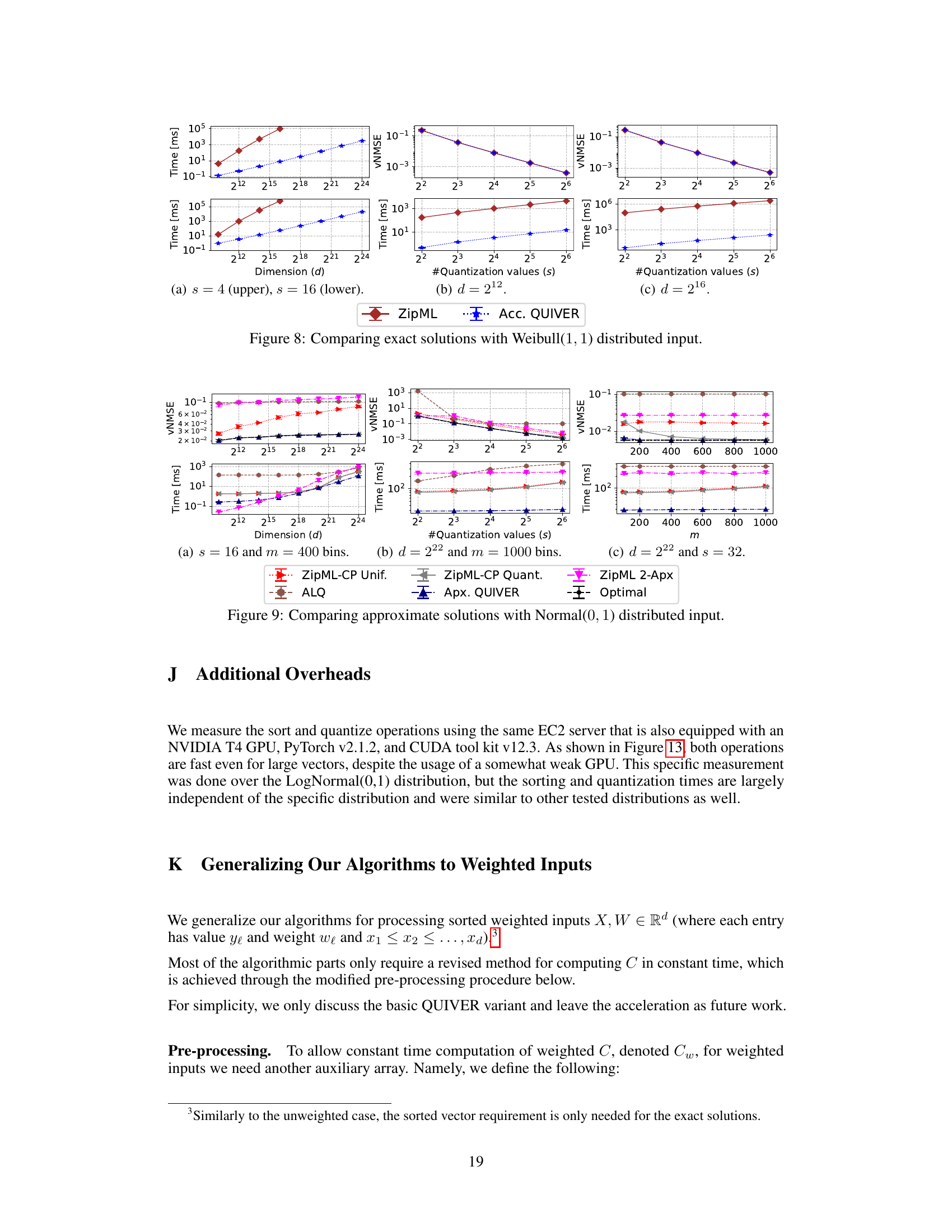
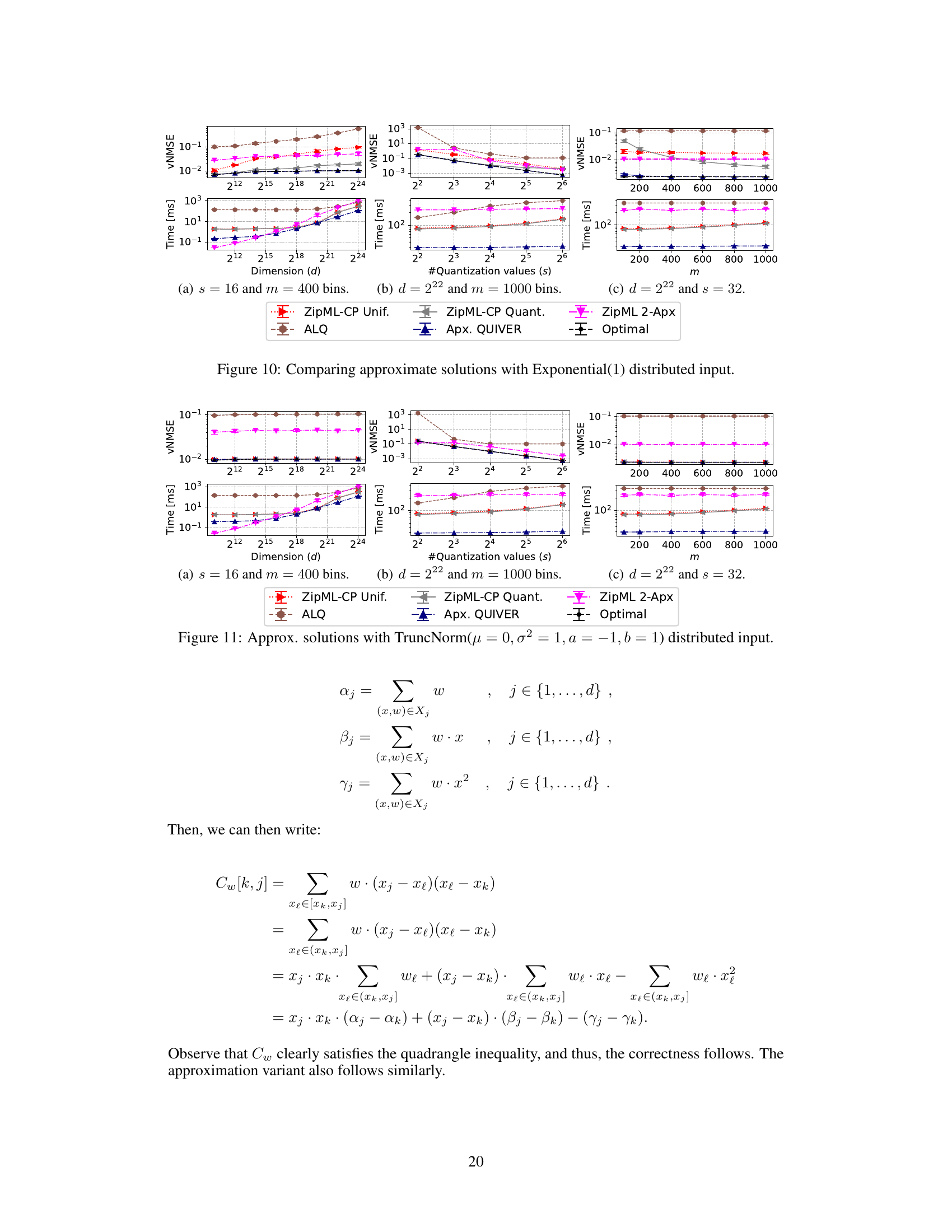
TL;DR#
Adaptive Stochastic Quantization (ASQ) is a crucial technique in machine learning for efficiently reducing memory and computational costs during model training and inference. However, existing ASQ methods are computationally expensive and thus impractical for large-scale applications. This has limited its use despite its superior accuracy over traditional quantization methods.
This paper introduces QUIVER, a novel algorithm that solves the ASQ problem optimally and efficiently. By leveraging a novel acceleration technique and the inherent properties of the problem, QUIVER reduces the time and space complexities significantly. This allows for optimal quantization of high-dimensional data that was previously impossible. The paper further introduces an accelerated version of QUIVER and an approximate variant for memory-constrained scenarios. Experiments demonstrate that these algorithms significantly outperform previous ASQ techniques, enabling the potential for more extensive use of ASQ in various ML applications.
Key Takeaways#
Why does it matter?#
This paper is crucial because it significantly advances adaptive stochastic quantization, a fundamental technique for optimizing machine learning applications. By presenting efficient algorithms, it enables the widespread adoption of ASQ, which can lead to faster training, reduced memory usage, and improved accuracy in various ML tasks. This opens new avenues for research in efficient quantization techniques for larger datasets and models.
Visual Insights#
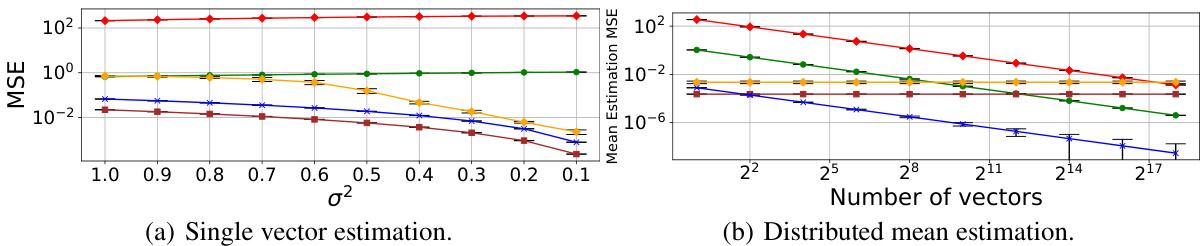
🔼 This figure compares the performance of adaptive and non-adaptive quantization methods for both single vector and distributed mean estimation tasks. It demonstrates that adaptive methods achieve lower mean squared error (MSE) than non-adaptive ones, and that the benefits of unbiased quantization are amplified in distributed settings.
read the caption
Figure 1: An experiment with dimension d = 10M and s = 10 quantization values. Figure 1(a) shows the empirical MSE of quantizing a single vector with i.i.d. LogNormal(0, σ2) entries. It shows that adaptive methods are more accurate than non-adaptive and that the optimal biased method is more accurate than the optimal unbiased one. However, as shown in Figure 1(b), for distributed mean estimation, the bias may not cancel out when averaging quantized inputs (here, we used a standard setup where all vectors are identical, e.g., see [17], with i.i.d. LogNormal(0, 1/2) distributed entries) and the advantage of unbiased methods accordingly increases with the number of inputs. Each data point is averaged over ten runs with the standard deviation reported.
In-depth insights#
ASQ Optimization#
Adaptive Stochastic Quantization (ASQ) optimization presents a significant challenge in machine learning, aiming to minimize quantization error by selecting quantization values specific to the input vector. Existing methods often face limitations in terms of computational cost and scalability, hindering their applicability to high-dimensional data. The core challenge lies in the non-convex nature of the optimization problem, rendering many standard approaches ineffective. Novel algorithms are crucial for efficient ASQ, focusing on reducing both time and space complexity, ideally achieving linear time complexity with respect to the input vector’s dimension. Clever preprocessing techniques may significantly speed up computation, while exploring the underlying mathematical structure of the problem could reveal further opportunities for optimization. Approximation algorithms that trade off accuracy for speed also have a significant role to play, particularly for real-time applications demanding rapid quantization of large datasets. The goal is to develop ASQ methods capable of handling high-dimensional data and offering an attractive balance between accuracy and computational efficiency.
QUIVER Algorithm#
The QUIVER algorithm, presented in the context of Adaptive Stochastic Quantization (ASQ), offers a novel approach to efficiently solve the ASQ problem. Its core innovation lies in leveraging the quadrangle inequality property of a specific matrix derived from the input data, enabling the use of the SMAWK algorithm for efficient row minima computation. This significantly improves the time and space complexity compared to previous ASQ methods. QUIVER achieves optimal solutions with improved asymptotic runtime and memory efficiency. Furthermore, the algorithm’s acceleration for the case of s=3 (three quantization values) provides a faster solution for arbitrary ’s’ by processing two values at a time. An approximation variant, Apx. QUIVER, trades a small amount of accuracy for a substantial speed increase, making it practical for real-time quantization of large vectors. The algorithm’s efficiency opens possibilities for more widespread adoption of ASQ in machine learning applications.
Accelerated QUIVER#
The Accelerated QUIVER algorithm presents a significant advancement in adaptive stochastic quantization. By leveraging the closed-form solution for the case of three quantization values (s=3), it achieves a substantial speedup compared to the original QUIVER algorithm. This optimization is crucial because it reduces the computational complexity, making the approach more practical for high-dimensional data commonly encountered in machine learning applications. The algorithm cleverly interleaves the closed-form solution with the SMAWK algorithm, resulting in a more efficient process that minimizes the mean squared error (MSE) while significantly reducing runtime. The speedup is particularly noticeable for odd values of ’s’, demonstrating the effectiveness of the strategy used. Ultimately, Accelerated QUIVER provides a powerful tool for achieving optimal or near-optimal adaptive quantization with dramatically improved efficiency. Its efficiency makes on-the-fly quantization feasible for various applications where speed is critical.
Approximation#
The approximation methods discussed in this research paper offer a compelling approach to address the computational demands of adaptive stochastic quantization (ASQ). By strategically discretizing the search space for optimal quantization values, the proposed approximate algorithm achieves a remarkable speedup. This trade-off between accuracy and computational efficiency is carefully managed and controlled by a parameter (m), allowing for flexibility in balancing these crucial aspects. The theoretical analysis and empirical evaluation of this approximation demonstrate its effectiveness, with performance approaching that of optimal solutions, especially for larger-scale applications. The algorithm’s ability to handle high-dimensional data and its near-optimal performance on various distributions underline its practical significance. The approximation strategy opens doors for real-time or on-the-fly quantization, making ASQ more broadly applicable in machine learning tasks.
Future Works#
Future work could explore several promising directions. Extending QUIVER to handle non-sorted input vectors efficiently is crucial for broader applicability. The current O(d log d) preprocessing step for sorting significantly impacts runtime. Investigating alternative data structures or approximation techniques could drastically improve performance. Parallel and GPU implementations of QUIVER and its variants are needed to scale to even larger datasets and models. A deeper theoretical analysis of the approximation guarantees of Apx. QUIVER would provide valuable insights into its accuracy and performance trade-offs. Finally, generalizing QUIVER to handle more complex quantization schemes (e.g., non-uniform quantization, biased quantization) and extending to scenarios beyond mean estimation are compelling avenues for future research.
More visual insights#
More on figures

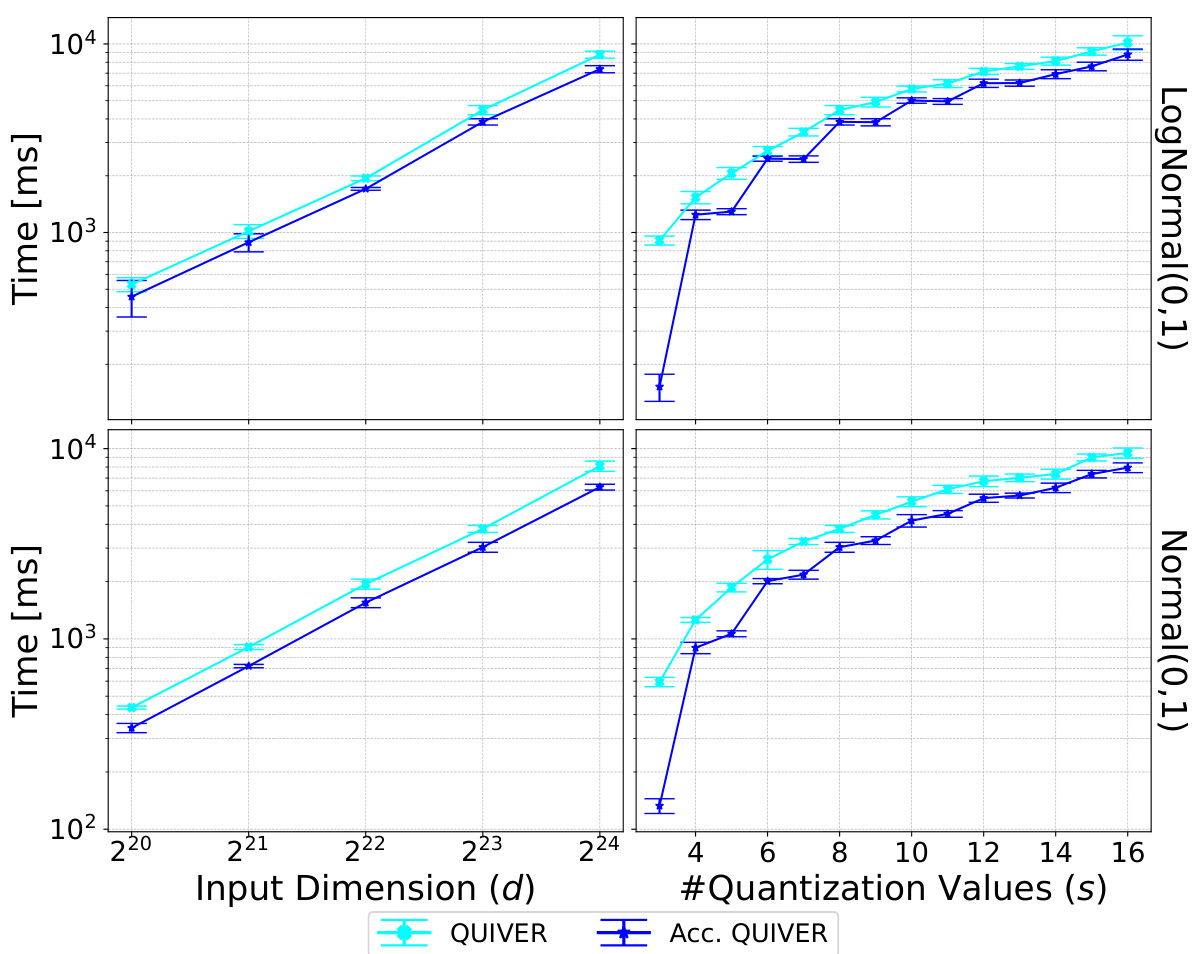
🔼 This figure compares the performance of ZipML and Accelerated QUIVER in terms of both runtime and normalized mean squared error (vNMSE) for different dimensions (d) and numbers of quantization values (s). The plots show that Accelerated QUIVER significantly outperforms ZipML in terms of speed, especially as the dimension and the number of quantization values increase. The vNMSE values show that both algorithms achieve similar accuracy, indicating that the speedup of Accelerated QUIVER comes without significant loss in quantization quality.
read the caption
Figure 2: Comparing exact solutions with LogNormal(0, 1) distributed input.
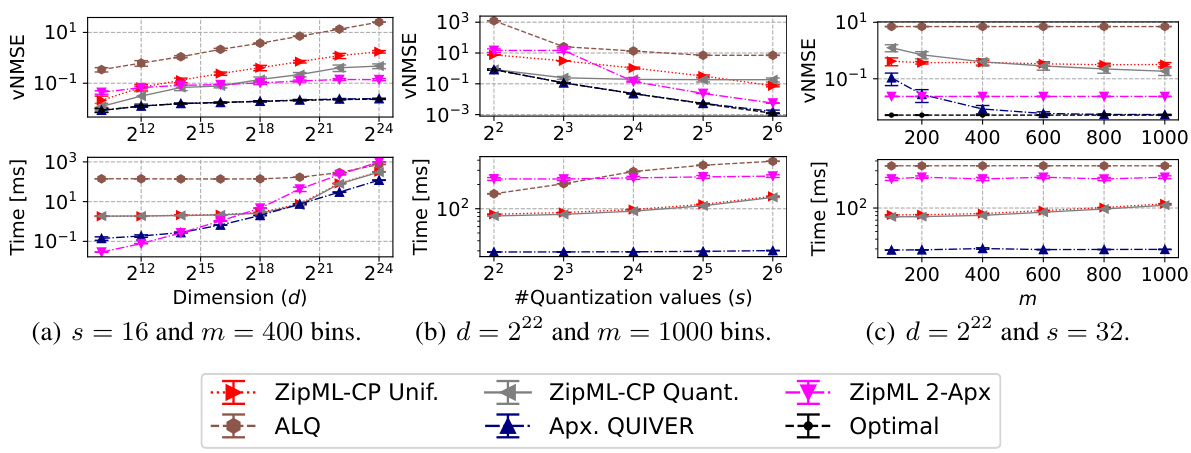
🔼 This figure compares the performance of several approximate adaptive stochastic quantization methods against the optimal solution for a LogNormal(0,1) distributed input. It shows the vNMSE (vertical normalized mean squared error) and runtime for different dimensions (d), numbers of quantization values (s), and discretization levels (m). The figure highlights the tradeoff between accuracy and speed for different approximate methods, and shows that Apx. QUIVER provides a good balance.
read the caption
Figure 3: Comparing approximate solutions with LogNormal(0, 1) distributed input.
🔼 This figure compares the performance of QUIVER and Accelerated QUIVER against ZipML for exact adaptive stochastic quantization. The plots show the runtime (in milliseconds) and vNMSE (vertical normalized mean squared error) for various input vector dimensions (d) and numbers of quantization values (s). It demonstrates the superior speed of QUIVER and Accelerated QUIVER compared to ZipML, especially as the problem size increases.
read the caption
Figure 4: Comparing exact solutions with LogNormal(0, 1) distributed input.

🔼 This figure compares the performance of ZipML and QUIVER algorithms in terms of both vNMSE (vector normalized mean squared error) and runtime. Subfigures (a), (b), and (c) show results varying dimension (d), the number of quantization values (s), and the dimension (d), respectively. The results demonstrate that QUIVER is significantly faster than ZipML while achieving comparable accuracy.
read the caption
Figure 2: Comparing exact solutions with LogNormal(0, 1) distributed input.
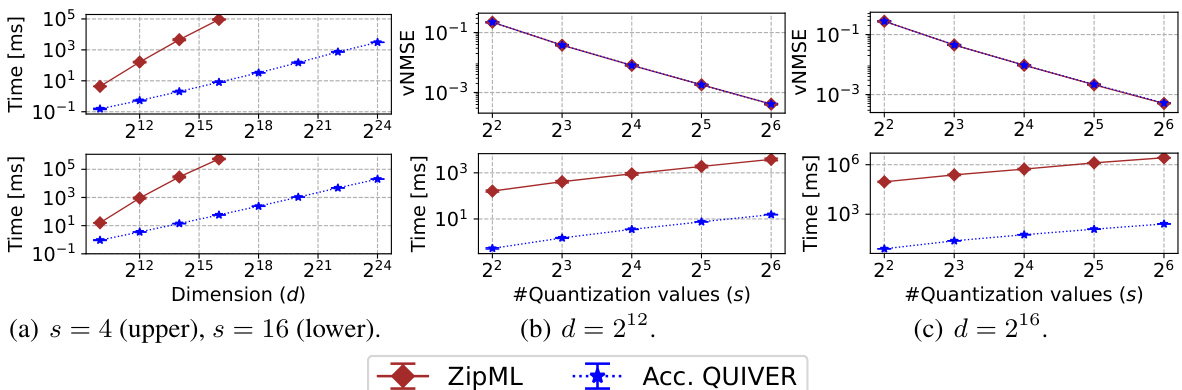
🔼 This figure compares the performance of ZipML and Accelerated QUIVER in terms of both runtime (in milliseconds) and vNMSE (vector-normalized mean squared error) across different dimensions (d) and numbers of quantization values (s). Subplots (a), (b), and (c) show the results when varying one parameter while holding others constant, providing a detailed analysis of the algorithms’ scaling behavior in different settings.
read the caption
Figure 2: Comparing exact solutions with LogNormal(0, 1) distributed input.

🔼 This figure compares the performance of ZipML and Accelerated QUIVER in terms of both vNMSE (vertical normalized mean squared error) and runtime. Subfigure (a) shows the results for different dimensions (d) and a fixed number of quantization values (s). Subfigures (b) and (c) show the results for a fixed dimension and varying numbers of quantization values. The results demonstrate that Accelerated QUIVER is significantly faster than ZipML while achieving comparable accuracy.
read the caption
Figure 2: Comparing exact solutions with LogNormal(0, 1) distributed input.
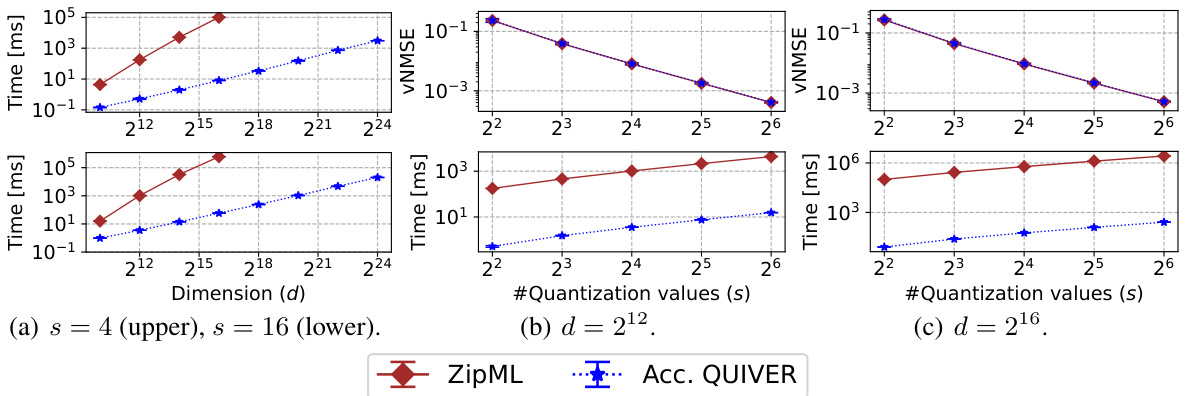
🔼 This figure compares the performance of ZipML and Accelerated QUIVER algorithms for exact adaptive stochastic quantization. Panel (a) shows the vNMSE and runtime for different dimensions (d) and a fixed number of quantization values (s). Panel (b) presents the vNMSE and runtime for varying ’s’ with a fixed ’d’ = 212. Panel (c) displays the vNMSE and runtime for varying ’s’ with a fixed ’d’ = 216. The results demonstrate that Accelerated QUIVER is significantly faster than ZipML while achieving comparable accuracy, especially as the dimension and number of quantization values increase.
read the caption
Figure 2: Comparing exact solutions with LogNormal(0, 1) distributed input.
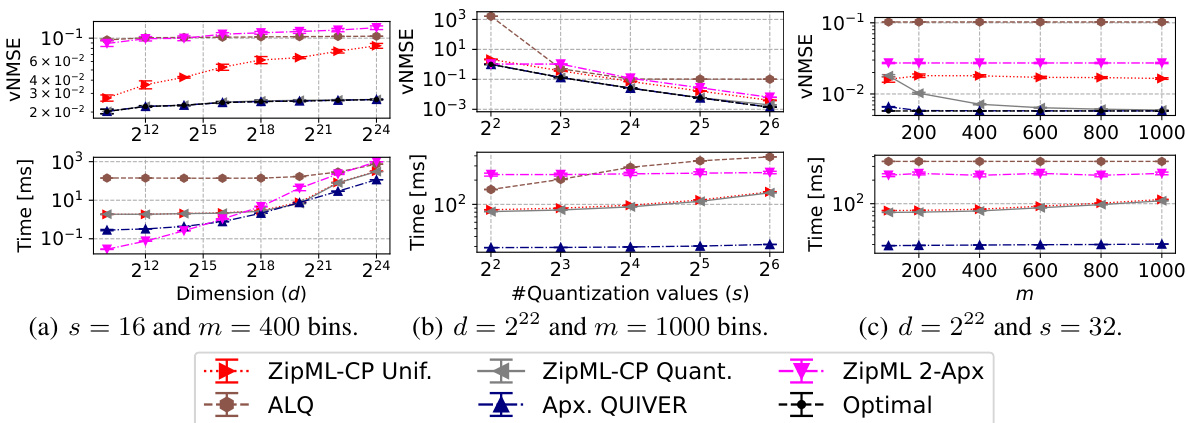
🔼 This figure compares the performance of several approximate adaptive stochastic quantization algorithms against the optimal solution for a LogNormal(0,1) distributed input. It shows vNMSE (vertical normalized mean squared error) and runtime (in milliseconds) across different dimensions (d), numbers of quantization values (s), and discretization levels (m) for Apx. QUIVER and several baselines (ZipML-CP Unif, ZipML-CP Quant, ZipML 2-Apx, ALQ). The results demonstrate Apx. QUIVER’s speed and accuracy advantages, especially as the problem size increases.
read the caption
Figure 3: Comparing approximate solutions with LogNormal(0, 1) distributed input.

🔼 This figure compares the performance of various approximate adaptive stochastic quantization methods against the optimal solution for LogNormal(0,1) distributed input. It demonstrates the runtime and vNMSE (vector normalized mean squared error) for different dimensions (d), numbers of quantization values (s), and discretization levels (m). The results showcase the tradeoff between speed and accuracy of approximate methods, highlighting the efficiency of Apx. QUIVER (Approximate QUIVER) in achieving near-optimal results with significantly faster computation.
read the caption
Figure 3: Comparing approximate solutions with LogNormal(0, 1) distributed input.
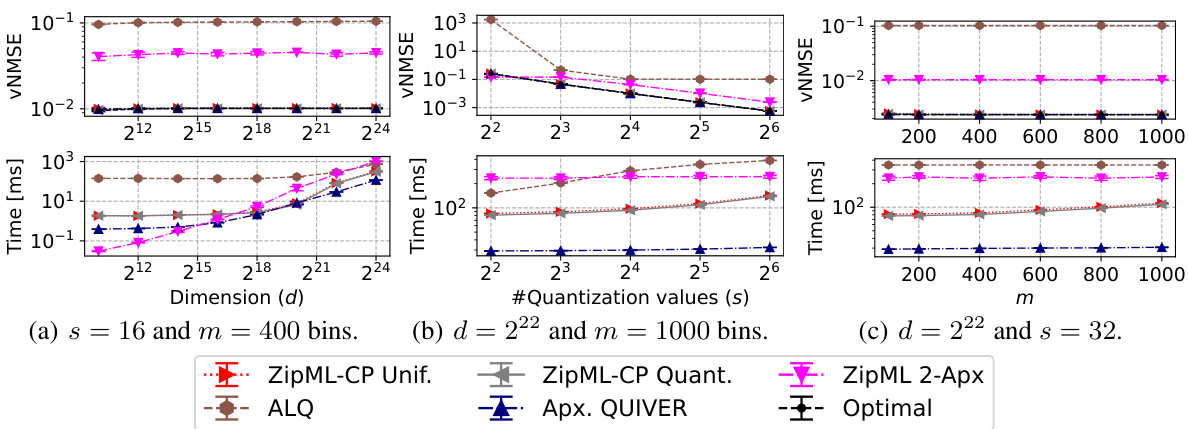
🔼 This figure compares the performance of several approximate adaptive stochastic quantization algorithms against the optimal solution for a LogNormal(0, 1) distributed input. It shows the vNMSE (vertical normalized mean squared error) and runtime (in milliseconds) for different dimensions (d), numbers of quantization values (s), and discretization levels (m). The algorithms compared are ZipML-CP Unif., ZipML-CP Quant., ZipML 2-Apx, ALQ, and Apx. QUIVER. The figure helps to illustrate the trade-offs between accuracy and speed for different approximate methods and the effectiveness of the proposed Apx. QUIVER algorithm.
read the caption
Figure 3: Comparing approximate solutions with LogNormal(0, 1) distributed input.
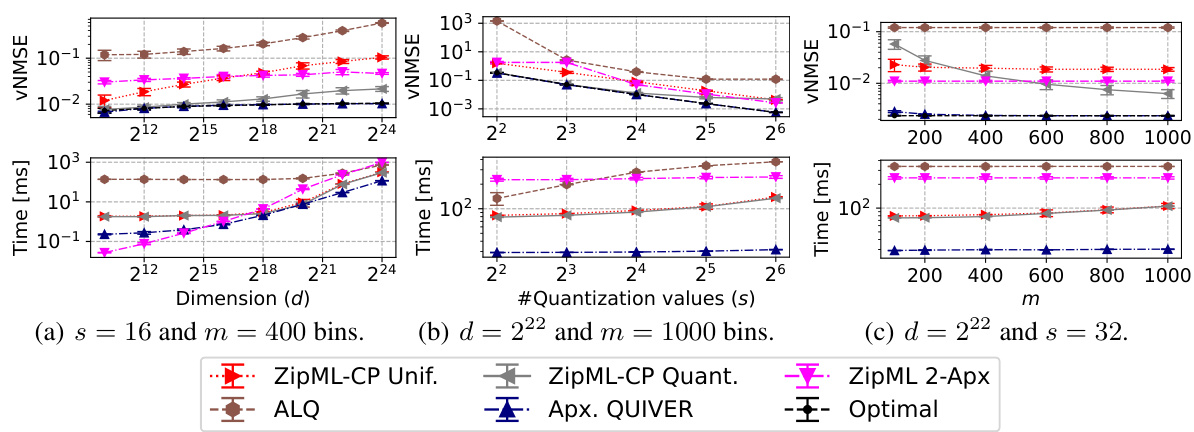
🔼 This figure compares the performance of various approximate adaptive stochastic quantization algorithms against the optimal solution. Subfigures (a), (b), and (c) show the results with respect to varying dimensions of the input vector, number of quantization values, and the discretization level (number of bins) of the search space, respectively. The algorithms being compared include ZipML-CP Quantiles, ZipML-CP Uniform, ZipML 2-Approximation, ALQ, and the proposed Approximate QUIVER algorithm. It demonstrates the tradeoffs between accuracy and speed and shows that Approximate QUIVER provides a good balance by offering near-optimal accuracy and the fastest runtime.
read the caption
Figure 3: Comparing approximate solutions with LogNormal(0, 1) distributed input.
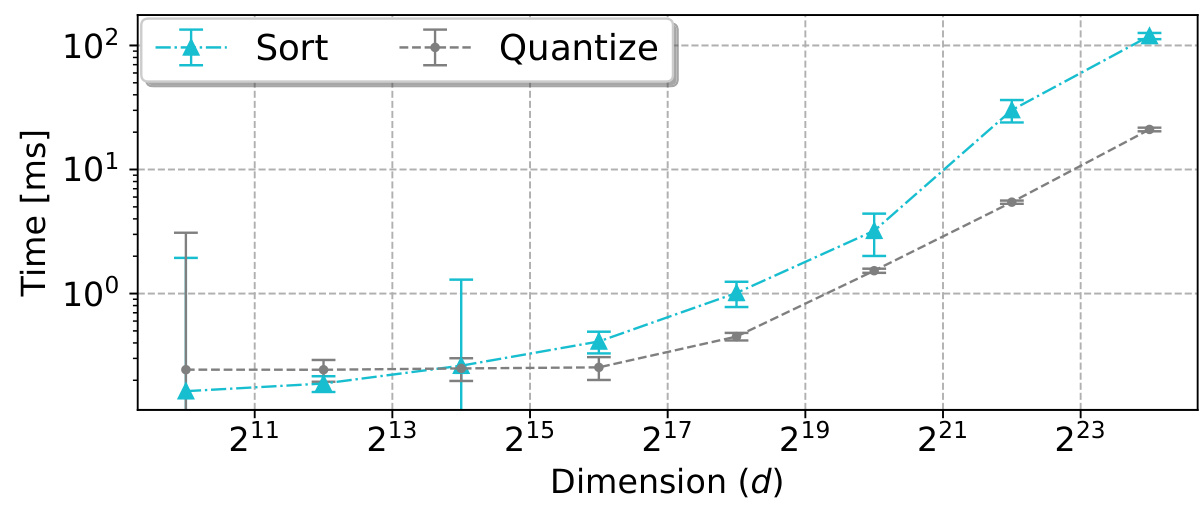
🔼 The figure shows the time taken for sorting and quantization operations using a T4 GPU, with the number of quantization values fixed at 16. The x-axis represents the dimension (d) of the input vector, and the y-axis represents the time in milliseconds. The plot shows that the time for both operations increases with the dimension of the input vector, with quantization taking significantly longer than sorting, especially for larger dimensions. Error bars show standard deviation across multiple runs.
read the caption
Figure 13: Sort and quantization times (s = 16) vs. d on a T4 GPU.
Full paper#