TL;DR#
Online multiclass classification is challenging when feedback is limited (bandit feedback), unlike full-information scenarios. This paper investigates how this limited feedback, along with the adversary’s adaptivity and learner’s use of randomness, affects learning performance, measured by mistake bounds. Prior work primarily focused on deterministic learners, leaving many questions unanswered.
The researchers present a comprehensive analysis by exploring several scenarios with various combinations of full/bandit feedback, adaptive/oblivious adversaries, and randomized/deterministic learners. They derive nearly tight bounds on the optimal mistake bounds for these scenarios, offering answers to previously open questions, and identifying significant impacts of learner randomization and adversary adaptivity on the mistake bounds in the bandit feedback settings.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses a critical gap in online multiclass classification. It provides nearly tight bounds on the tradeoffs between various learning scenarios, resolving open questions and offering valuable insights for algorithm design and performance analysis. The results are particularly relevant to the growing field of bandit feedback learning, where full information is not always available. Researchers can leverage these findings to develop more efficient and robust algorithms, particularly in online learning settings with limited feedback.
Visual Insights#

🔼 BanditRandSOA is an algorithm for online learning with bandit feedback. It’s optimal for pattern classes when the adversary is adaptive. The algorithm is inspired by the RandSOA algorithm and Littlestone’s SOA algorithm.
read the caption
Figure 1: BanditRandSOA is an optimal randomized learner for online learning with bandit feedback of pattern classes, where the adversary is allowed to be adaptive. It is inspired by the RandSOA algorithm of Filmus, Hanneke, Mehalel, and Moran [2023], which is a randomized variant of Littlestnoe’s [Littlestone, 1988] well-known SOA algorithm.

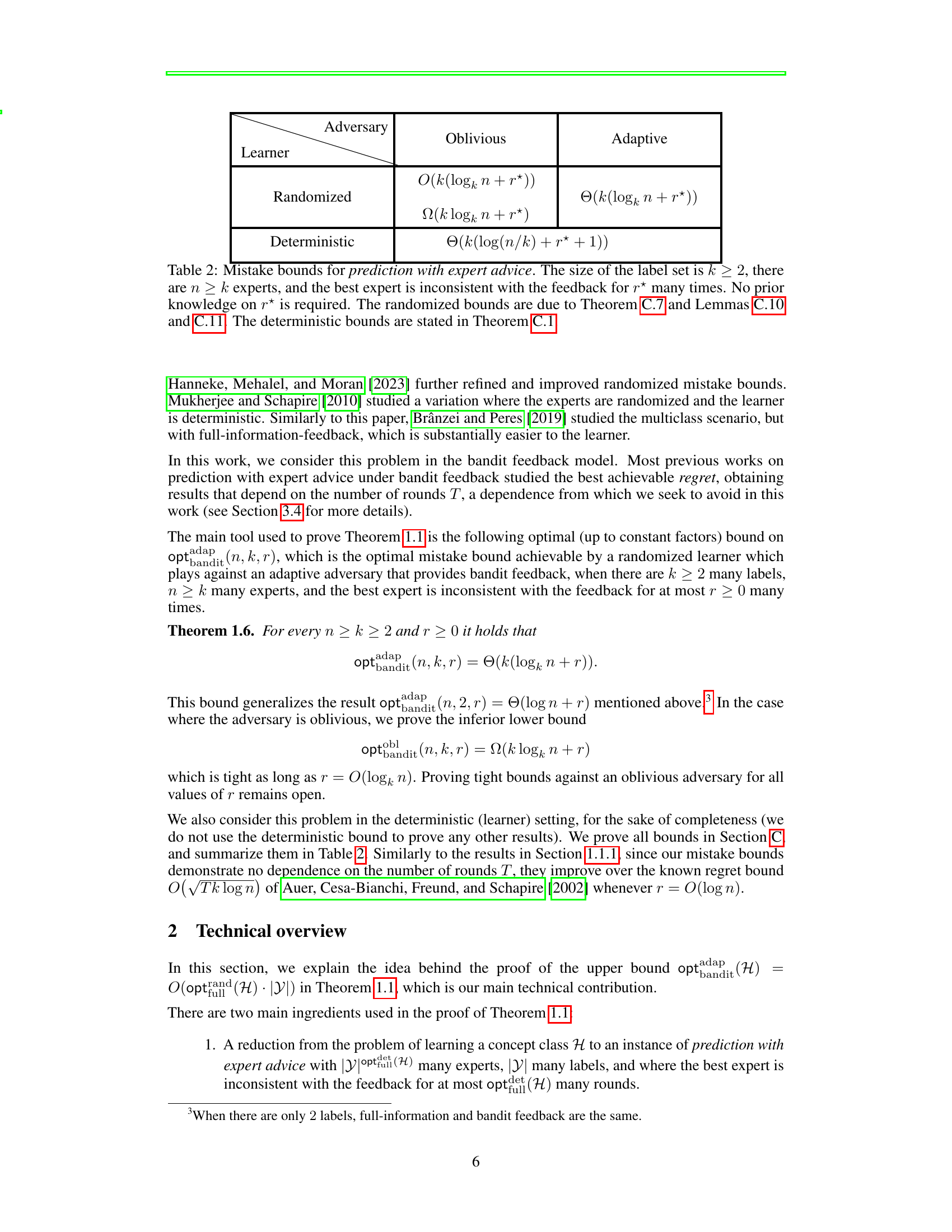
🔼 This table presents the mistake bounds for prediction with expert advice under different settings. The settings vary based on whether the learner is randomized or deterministic, and whether the adversary is oblivious or adaptive. The bounds account for the number of labels (k), the number of experts (n), and the number of times the best expert is inconsistent with the feedback (r*).
read the caption
Table 2: Mistake bounds for prediction with expert advice. The size of the label set is k ≥ 2, there are n ≥ k experts, and the best expert is inconsistent with the feedback for r* many times. No prior knowledge on r* is required. The randomized bounds are due to Theorem C.7 and Lemmas C.10 and C.11. The deterministic bounds are stated in Theorem C.1.
Full paper#