TL;DR#
Current approaches to game AI often rely on rigid, game-specific architectures like Convolutional Neural Networks (CNNs), limiting adaptability and scalability. For instance, a model trained for 19x19 Go struggles to adapt to 13x13 Go, despite shared underlying rules. This inflexibility also leads to high computational costs for training models from scratch for each game variant.
This research introduces AlphaGateau, a novel approach using Graph Neural Networks (GNNs) and a modified Graph Attention Network (GAT) layer called GATEAU, which naturally incorporate edge features for policy output. Experiments show that AlphaGateau significantly outperforms previous architectures with similar parameters, achieving a magnitude order of increased playing strength with faster training times. Crucially, a model trained on a smaller 5x5 chess variant quickly adapts to the standard 8x8 chessboard, illustrating impressive generalization.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel approach to chess reinforcement learning, demonstrating superior performance and generalization abilities compared to existing methods. Its use of graph neural networks and a novel attention mechanism offers a more adaptable and scalable solution, opening new avenues for research in game AI and beyond. The faster training times and improved generalization capabilities are significant advancements, with implications for other complex decision-making problems.
Visual Insights#

🔼 This figure shows the architecture of the AlphaGateau neural network. It consists of two main branches, one for processing node features (representing squares on the chessboard) and another for processing edge features (representing moves). Node features are first processed through linear layers and then fed into a series of ResGATEAU (residual GATEAU) blocks. Similarly, edge features are processed through linear layers before being fed into the ResGATEAU blocks. The outputs of the ResGATEAU blocks are then used to predict the value (game outcome) and policy (move probabilities) of a given game state.
read the caption
Figure 2: The AlphaGateau network, hs is the inner size of the feature vectors, and L is the number of residual blocks.
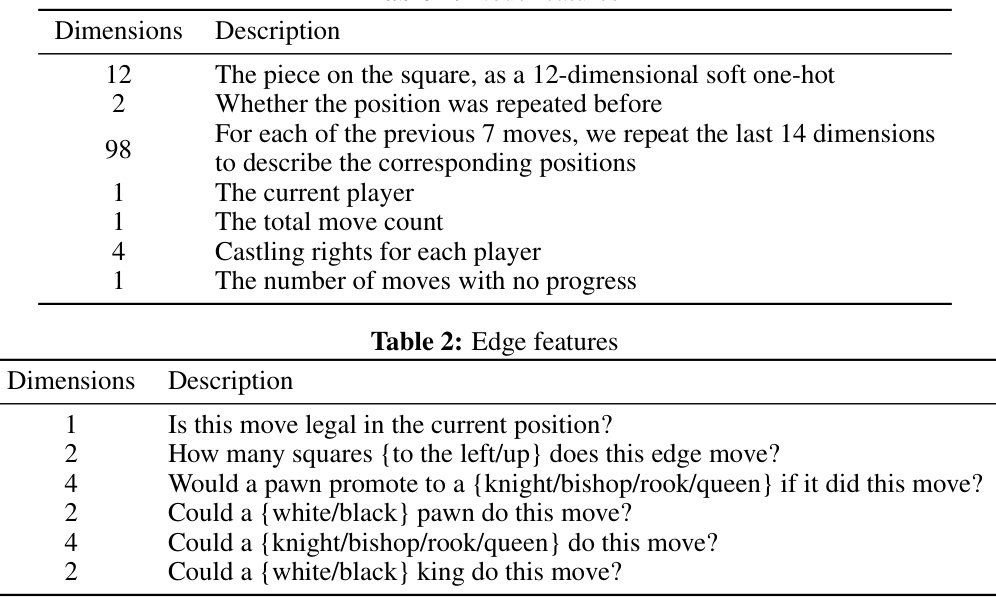
🔼 This table describes the features used to represent each node (square) in the graph-based representation of a chessboard state. Each node has a feature vector composed of 12 dimensions indicating the piece type, 2 dimensions indicating whether the position has been repeated before in the game, 98 dimensions describing the positions of pieces for the last 7 moves, and 5 additional dimensions representing the current player, the total move count, castling rights, and the number of moves without progress. This rich node feature set allows the model to capture complex game states.
read the caption
Table 1: Node features
In-depth insights#
Graph-Based Chess#
A graph-based approach to representing chess offers significant advantages over traditional grid-based methods. By representing pieces as nodes and moves as edges, this approach allows for a more natural and flexible representation of the game state. This is particularly beneficial when dealing with variations in board size or different rule sets, as seen in the paper’s exploration of 5x5 chess. The use of Graph Neural Networks (GNNs) enables the model to learn relationships between pieces and moves, capturing strategic patterns more effectively. Edge features enhance the model’s ability to handle diverse move structures. This approach also has the potential for improved generalization to other games, suggesting a promising direction for future research in AI game playing.
GATEAU’s Edge#
The heading “GATEAU’s Edge” cleverly alludes to the core contribution of the Graph Attention Network with Edge features from Attention weight Updates (GATEAU) layer. This novel layer extends the classical GAT layer by integrating edge features alongside node features, thus enriching the network’s capacity to capture intricate relationships within a graph. This is particularly crucial in game contexts like chess, where the meaning of a move (edge) depends heavily on both the involved pieces (nodes) and the board’s overall state. By considering edge features, GATEAU transcends the limitations of standard GAT and enhances its ability to learn complex game strategies. This edge-aware approach allows for more nuanced policy predictions and a more expressive representation of the game state, directly impacting the model’s generalization performance and learning efficiency. The inclusion of edge features enables a more direct mapping between the model’s output and the actions taken within the game. This results in a significant advantage compared to traditional approaches that rely solely on node-based representations.
AlphaGateau’s Rise#
The hypothetical section “AlphaGateau’s Rise” would detail the model’s performance trajectory. It would likely begin by establishing a baseline, comparing AlphaGateau’s initial Elo rating against established chess AI benchmarks. The narrative would then trace AlphaGateau’s learning curve, highlighting its rapid improvement in playing strength over training iterations. Crucially, the analysis would emphasize the efficiency gains of AlphaGateau, demonstrating how it surpasses prior models in reaching competitive Elo scores while using considerably fewer computational resources. Generalization ability would be a key theme, showcasing AlphaGateau’s capacity to transfer knowledge from a smaller 5x5 chessboard to a standard 8x8 board with minimal additional training. This section would use graphs and charts to visually represent AlphaGateau’s Elo progression, emphasizing the significant jump in performance compared to alternatives, ultimately demonstrating its superior learning speed and adaptability.
Generalization Power#
The research paper investigates the generalization capabilities of AlphaGateau, a novel architecture designed for chess reinforcement learning. A key aspect explored is its ability to transfer knowledge learned from a smaller 5x5 chessboard to a standard 8x8 board. This showcases AlphaGateau’s ability to generalize beyond the specific training environment. The successful fine-tuning demonstrates strong generalization power, suggesting that the model learns fundamental chess principles rather than merely memorizing patterns. This is a significant advantage over previous approaches that often relied on rigid game-specific architectures with limited transferability. The faster training speed observed in AlphaGateau, combined with its generalization ability, makes it a promising model for future research in game AI. Further investigation into AlphaGateau’s generalization across different games and game variants is warranted, to assess its applicability beyond chess and uncover the extent of its potential in broader AI applications.
Future Directions#
Future research could explore several promising avenues. Extending the AlphaGateau architecture to deeper networks (beyond the 5-6 layers used here) and evaluating its performance against a full-scale, 40-layer AlphaZero model would validate the scalability and true potential of the graph-based approach. Investigating alternative graph representations for chess (or other games) could further optimize the model’s ability to capture strategic nuances. Exploring different GNN layers is necessary, as the current choice was largely based on simplicity and ease of implementation. Applying AlphaGateau to other games, particularly those with more complex move sets like Shogi or Go, and games that do not map easily to a grid-based representation would demonstrate its generalizability. Finally, researching efficient methods for managing the frame window in self-play training is crucial for handling larger datasets and improving generalization. This could involve exploring strategies to better select and sample data from the history, potentially with sophisticated similarity metrics between chess positions.
More visual insights#
More on figures
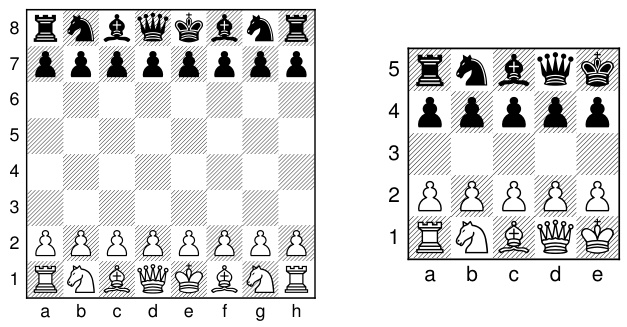
🔼 This figure shows the initial setup of chessboards for both standard 8x8 chess and a smaller 5x5 variant. The arrangement of pieces is the same in both, but scaled down in the 5x5 version. This highlights the similarity in game structure despite the difference in board size, which is relevant to the paper’s exploration of generalizing chess models across different board sizes.
read the caption
Figure 1: The starting positions of 8 × 8 and 5 × 5 chess games
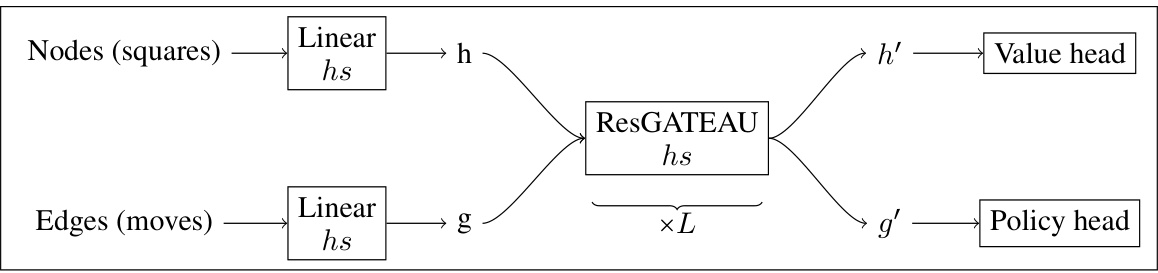
🔼 This figure shows the architecture of the AlphaGateau network. It’s a graph neural network that processes both node features (representing squares on the chessboard) and edge features (representing moves). Node features are first passed through a linear layer, then multiple residual GATEAU layers (a modified GAT layer handling edge features) process both node and edge features. Finally, the processed node and edge features are fed into separate linear layers that predict the value (game outcome) and policy (move probabilities), respectively. The ‘×L’ indicates that the residual GATEAU block is repeated L times, making the model deeper and more powerful.
read the caption
Figure 2: The AlphaGateau network, hs is the inner size of the feature vectors, and L is the number of residual blocks.
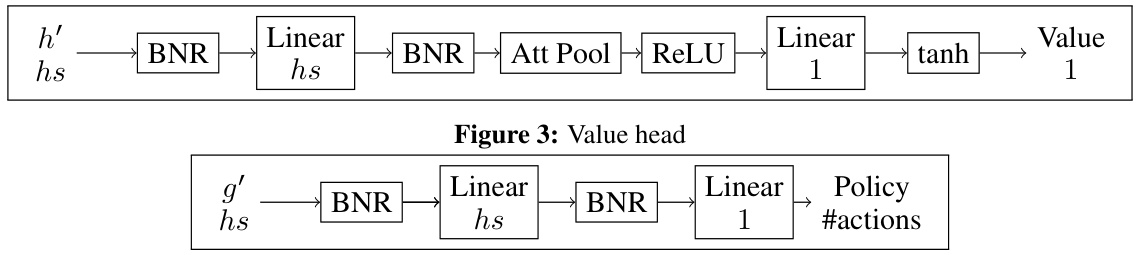
🔼 This figure shows the architecture of the value head in the AlphaGateau model. The value head takes node features as input and uses batch normalization (BNR), linear layers, attention pooling, and a ReLU activation function to output a single value representing the game state’s evaluation.
read the caption
Figure 3: Value head

🔼 This figure shows the architecture of the AlphaGateau neural network. The network processes both node features (representing squares on the chessboard) and edge features (representing moves). Node features are processed through a linear layer and then multiple residual GATEAU blocks (a novel GNN layer incorporating edge features) before being passed to the value head. Edge features also go through a linear layer and the same residual GATEAU blocks before being passed to the policy head. The number of residual blocks, L, and the inner size of the feature vectors, hs, are hyperparameters.
read the caption
Figure 2: The AlphaGateau network, hs is the inner size of the feature vectors, and L is the number of residual blocks.
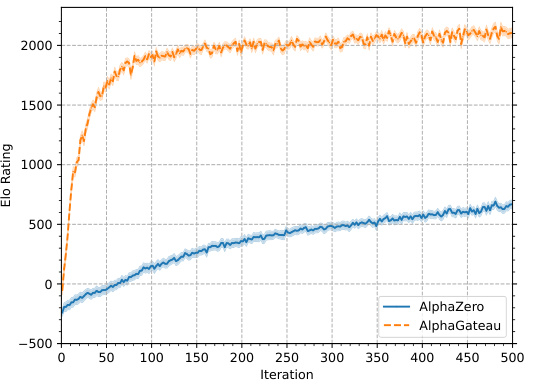
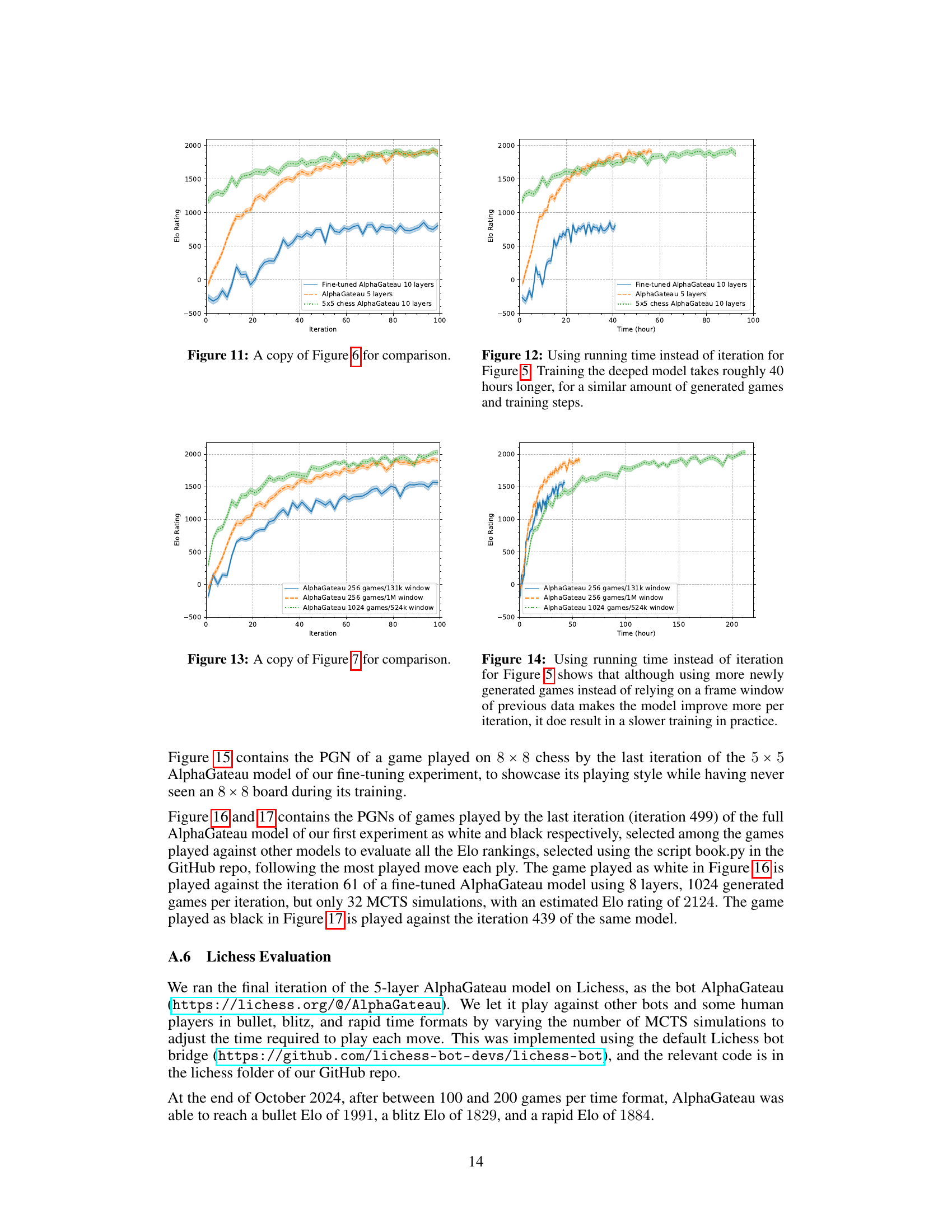
🔼 This figure shows the Elo ratings of two chess-playing models, AlphaZero and AlphaGateau, over 500 training iterations. AlphaGateau demonstrates significantly faster initial learning, achieving a comparable learning rate to AlphaZero after approximately 100 iterations.
read the caption
Figure 5: The Elo ratings of AlphaZero and AlphaGateau with 5 residual layers trained over 500 iterations. The AlphaGateau model initially learns ~10 times faster than the AlphaZero model, and settles after 100 iterations to a comparable speed of growth to that of AlphaZero.
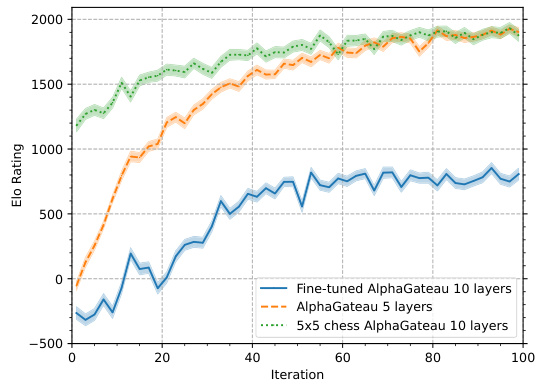
🔼 This figure compares the Elo ratings over the first 100 iterations for three different models: a 10-layer AlphaGateau model fine-tuned on an 8x8 chessboard after initial training on a 5x5 board, a 5-layer AlphaGateau model trained directly on an 8x8 board, and a 10-layer AlphaGateau model trained only on a 5x5 board. The plot demonstrates AlphaGateau’s ability to generalize from a smaller board size (5x5) to a larger one (8x8), even without explicit training on the larger board. The fine-tuned model shows a rapid increase in Elo rating upon transfer to the 8x8 board, exceeding the performance of the 5-layer model trained directly on 8x8.
read the caption
Figure 6: The Elo ratings of the first 100 iterations of the AlphaGateau model from Figure 5 was included for comparison. The initial training on 5×5 chess is able to increase its rating while evaluated on 8 × 8 chess during training, even without seeing any 8 × 8 chess position. The fine-tuned model starts with a good baseline, and reaches comparable performances to the 5-layer model despite being undertrained for its size.

🔼 This figure shows the impact of frame window size and the number of self-play games on model performance and training time. Using only the most recently generated games (131k window) resulted in the worst performance and fastest training time. Increasing the frame window size to 1M improved performance but still resulted in relatively fast training. Generating 1024 games per iteration with a 524k window resulted in the best performance but took significantly longer to train.
read the caption
Figure 7: The two models with a frame window of size 131 072 only kept the latest generated games in the frame window. The model keeping no frame window and generating 256 games was trained in only 39 hours, but had the worst performance. Adding a 1M frame window improved the performance a little and lasted 60 hours, while increasing the number of self-play games to 1024 performed the best, but took 198 hours.
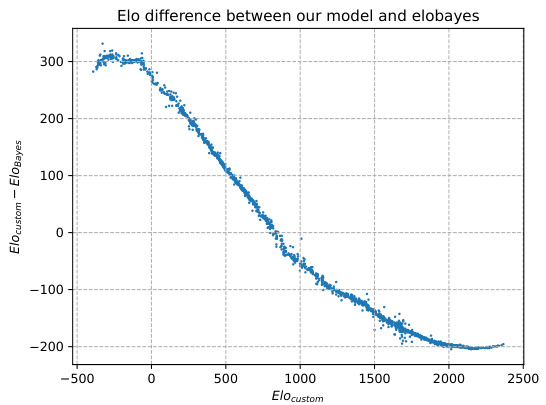
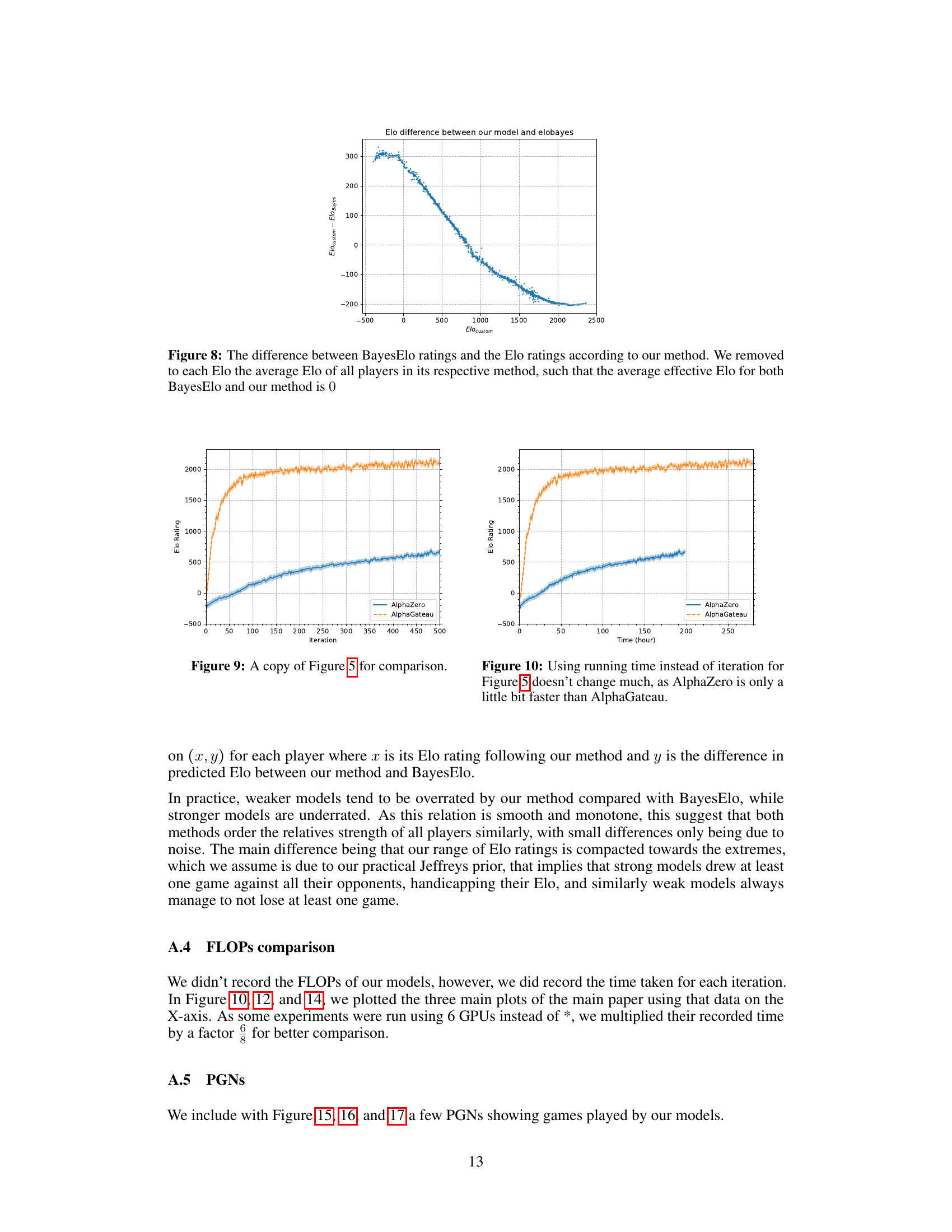
🔼 This figure shows the difference between the Elo ratings calculated using the authors’ custom method and the BayesElo method. The y-axis represents the difference in Elo ratings (custom - BayesElo), and the x-axis represents the Elo rating calculated by the authors’ custom method. Each point represents a player’s Elo rating. The plot reveals that weaker models (lower Elo) tend to be slightly over-rated by the authors’ custom method compared to BayesElo, while stronger models (higher Elo) are slightly under-rated. The trend suggests that while the two methods show similar rankings, there is a systematic difference. The authors hypothesize this difference might arise from their use of a Jeffreys prior in their method, affecting the estimation of Elo differences.
read the caption
Figure 8: The difference between BayesElo ratings and the Elo ratings according to our method. We removed to each Elo the average Elo of all players in its respective method, such that the average effective Elo for both BayesElo and our method is 0
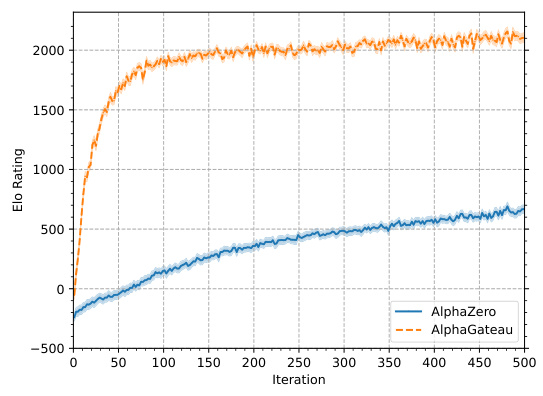
🔼 This figure shows the Elo ratings of two chess-playing agents, AlphaZero and AlphaGateau, over 500 training iterations. AlphaGateau, with a simpler architecture, demonstrates significantly faster initial learning, achieving a similar learning rate to AlphaZero after approximately 100 iterations.
read the caption
Figure 5: The Elo ratings of AlphaZero and AlphaGateau with 5 residual layers trained over 500 iterations. The AlphaGateau model initially learns ~10 times faster than the AlphaZero model, and settles after 100 iterations to a comparable speed of growth to that of AlphaZero.

🔼 This figure shows the Elo ratings of two chess-playing models, AlphaZero and AlphaGateau, over 500 training iterations. AlphaGateau demonstrates significantly faster initial learning, achieving a comparable learning rate to AlphaZero after 100 iterations.
read the caption
Figure 5: The Elo ratings of AlphaZero and AlphaGateau with 5 residual layers trained over 500 iterations. The AlphaGateau model initially learns ~10 times faster than the AlphaZero model, and settles after 100 iterations to a comparable speed of growth to that of AlphaZero.
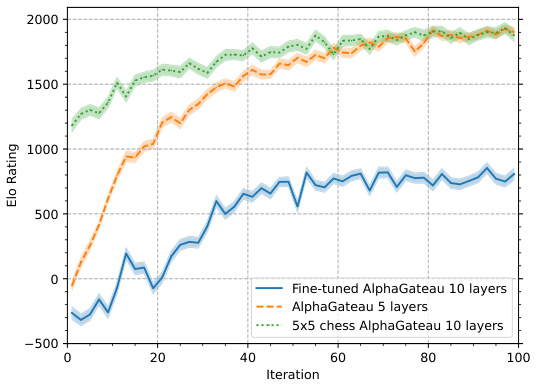
🔼 This figure compares the Elo ratings (a measure of skill in chess) of three different AlphaGateau models over 100 training iterations. One model was trained from scratch on 8x8 chess (standard size), another was initially trained on a smaller 5x5 chessboard and then fine-tuned on 8x8 chess, and the third was a smaller 5-layer model trained only on 8x8 chess. The graph shows that the model pretrained on 5x5 chess exhibits strong generalization, achieving a high Elo rating after fine-tuning, while the 5-layer model serves as a baseline.
read the caption
Figure 6: The Elo ratings of the first 100 iterations of the AlphaGateau model from Figure 5 was included for comparison. The initial training on 5×5 chess is able to increase its rating while evaluated on 8 × 8 chess during training, even without seeing any 8 × 8 chess position. The fine-tuned model starts with a good baseline, and reaches comparable performances to the 5-layer model despite being undertrained for its size.
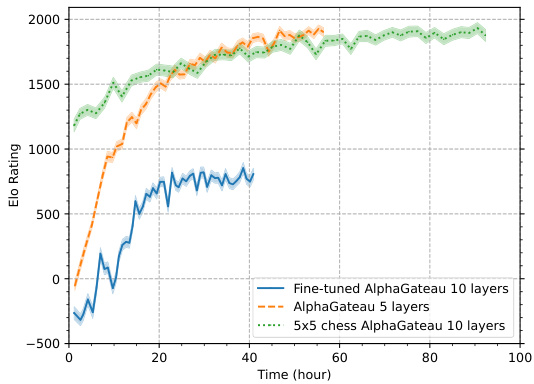
🔼 This figure compares the Elo ratings of three different AlphaGateau models over time, using training time in hours instead of iterations as in Figure 5. It shows that while the 5-layer AlphaGateau model and the 10-layer model trained on 5x5 chess achieve similar Elo ratings relatively quickly, the 10-layer model fine-tuned from 5x5 to 8x8 chess shows a longer training time but ultimately reaches higher Elo ratings. The additional training time for the deeper model highlights the trade-off between model complexity and training speed.
read the caption
Figure 12: Using running time instead of iteration for Figure 5. Training the deeped model takes roughly 40 hours longer, for a similar amount of generated games and training steps.
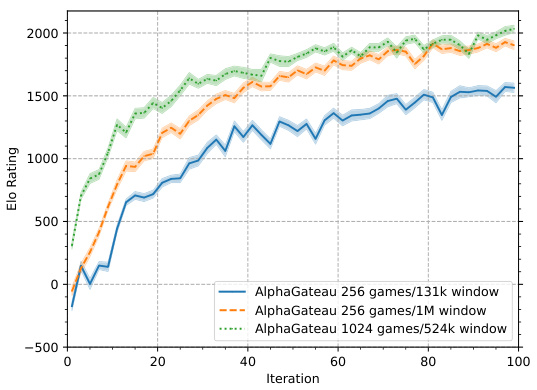
🔼 This figure compares the performance of three AlphaGateau models trained with different frame window sizes and numbers of self-play games. The results show that using a larger frame window and a greater number of self-play games improves performance, although it significantly increases training time. The model with a 1M frame window and 256 games per iteration took 60 hours to train, showing modest improvement over the model with no frame window, which took only 39 hours but performed worst. The model with 1024 games and a 524k window, which was the best-performing model, required 198 hours of training.
read the caption
Figure 7: The two models with a frame window of size 131 072 only kept the latest generated games in the frame window. The model keeping no frame window and generating 256 games was trained in only 39 hours, but had the worst performance. Adding a 1M frame window improved the performance a little and lasted 60 hours, while increasing the number of self-play games to 1024 performed the best, but took 198 hours.

🔼 This figure compares the performance of three AlphaGateau models trained with different frame window sizes and numbers of self-play games. The model using only the latest generated games (131k window) performed the worst, while the model using a larger frame window (1M) and more games showed improvement. The best performance was achieved using a larger frame window (524k) and even more games (1024), although at the cost of significantly increased training time.
read the caption
Figure 7: The two models with a frame window of size 131 072 only kept the latest generated games in the frame window. The model keeping no frame window and generating 256 games was trained in only 39 hours, but had the worst performance. Adding a 1M frame window improved the performance a little and lasted 60 hours, while increasing the number of self-play games to 1024 performed the best, but took 198 hours.
Full paper#