TL;DR#
Matrix factorization models are frequently used in machine learning, particularly for tasks like matrix completion (filling in missing data). While low nuclear norm and low rank regularizations are common, a comprehensive understanding of their differing implicit regularization effects was lacking. This paper identifies a key challenge: the existing literature provides conflicting perspectives on implicit regularization. Some argue for low nuclear norm, while others argue for low rank.
This research systematically investigates this issue through extensive experiments and theoretical analysis. The core finding is that the connectivity of the observed data dictates the implicit bias, with low nuclear norm favored when data is disconnected and low rank when data is connected. The researchers identify hierarchical invariant manifolds in the model’s loss landscape, which guides the training trajectory. They also provide theoretical conditions for guaranteeing minimum nuclear norm and minimum rank solutions, reinforcing their empirical findings. This work significantly enhances our understanding of implicit regularization in matrix factorization.
Key Takeaways#
Why does it matter?#
This paper is crucial because it reveals the interplay between data connectivity and implicit regularization in matrix factorization, a widely used technique in machine learning. Understanding this relationship is key to improving model performance and generalization. The findings offer new avenues for theoretical analysis and algorithm design, with implications for various applications.
Visual Insights#

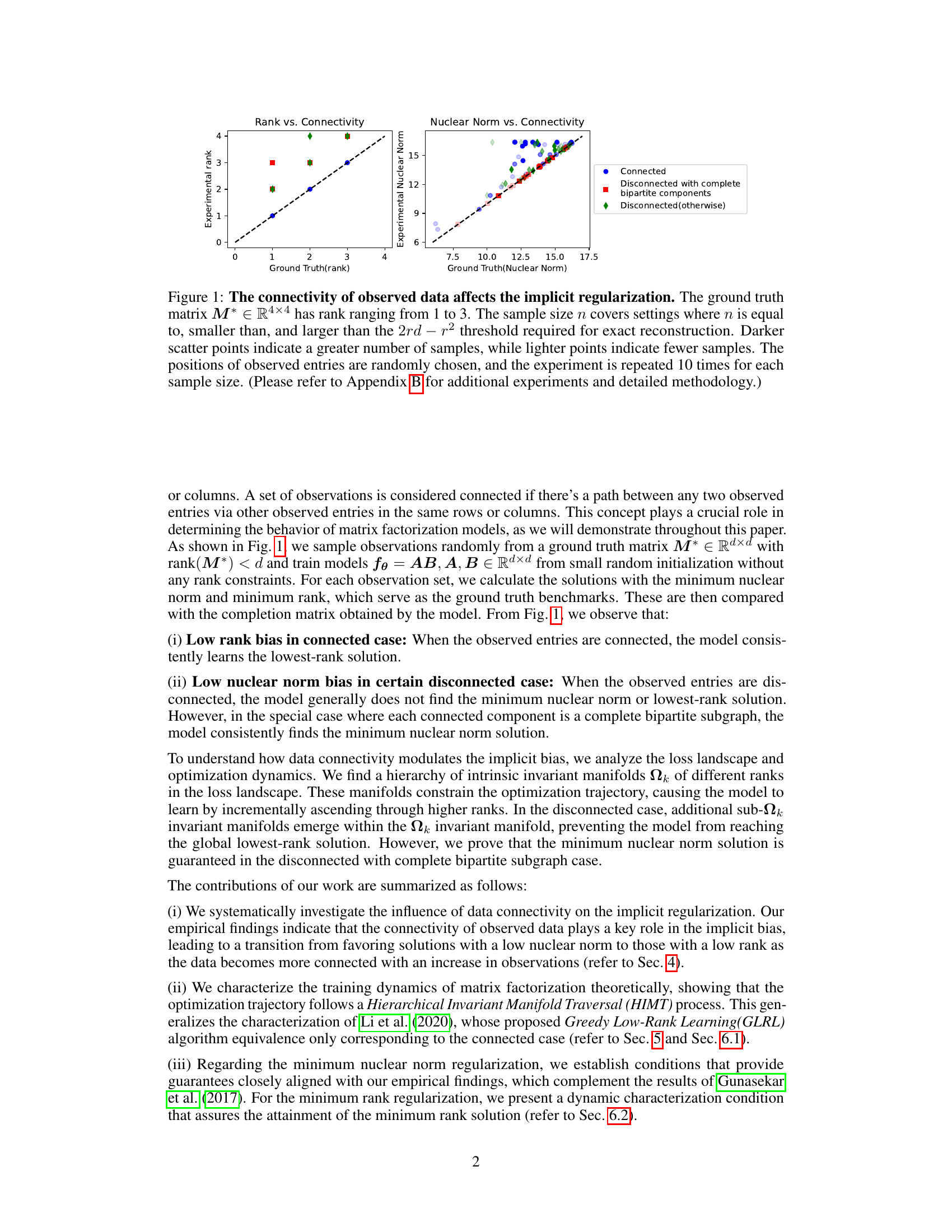
🔼 This figure shows the impact of observed data connectivity on implicit regularization in matrix factorization models for matrix completion. It compares the experimental rank and nuclear norm of solutions obtained from training matrix factorization models on datasets with varying connectivity (connected, disconnected with complete bipartite components, and other disconnected cases). The plot demonstrates a transition from low nuclear norm bias to low rank bias as the data connectivity increases, revealing a key role of data connectivity in shaping implicit regularization.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ ]R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)
In-depth insights#
Implicit Regularization#
Implicit regularization, a phenomenon where overparameterized models generalize well despite their capacity to memorize random labels, is a central theme in modern machine learning. The paper explores this concept within the context of matrix factorization models for matrix completion, focusing on how data connectivity shapes the implicit bias. Empirical findings reveal a transition from low nuclear norm regularization (disconnected data) to low rank regularization (connected data) as more observations become available. This transition is explained by the existence of hierarchical invariant manifolds in the loss landscape; these manifolds constrain the optimization trajectory, influencing the model’s tendency to learn low-rank or low-nuclear-norm solutions. The interplay between data connectivity, training dynamics, and implicit regularization is shown to be intricate. The authors theoretically characterize the training trajectory, generalizing previous work to account for the case of disconnected data, establishing conditions that guarantee the attainment of minimum nuclear norm and minimum rank solutions, thereby providing a comprehensive understanding of implicit regularization within matrix factorization models.
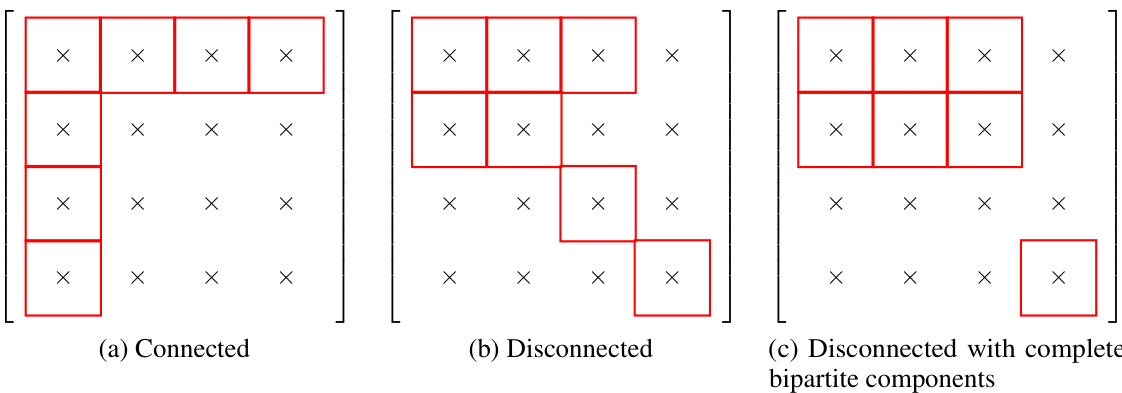
Connectivity’s Role#
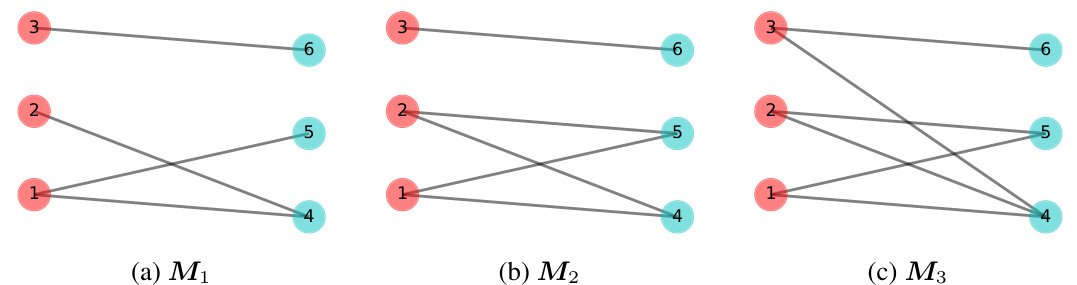
The research paper explores the impact of data connectivity on implicit regularization within matrix factorization models for matrix completion. Connectivity, defined by how observed data entries link through shared rows or columns, fundamentally alters the model’s implicit bias. With high connectivity, the model strongly favors low-rank solutions, aligning with previous research suggesting a preference for minimum rank. Low connectivity, however, leads to a shift towards low nuclear norm solutions, particularly when the data exhibits complete bipartite components. This nuanced relationship highlights the dynamic interplay between data structure and the model’s optimization process. The findings challenge the notion of a unified implicit regularization effect, instead revealing a dependence on the inherent structure of the observed data. This discovery is supported by theoretical analysis and experimental evidence, showcasing the existence of hierarchical invariant manifolds in the loss landscape that guide training trajectories toward solutions reflecting data connectivity. This intricate relationship provides valuable insights into the generalization capabilities of overparameterized models and opens avenues for future research exploring similar effects in more complex models.
Training Dynamics#
The study’s analysis of training dynamics reveals crucial insights into how data connectivity shapes implicit regularization in matrix factorization. In connected scenarios, the optimization trajectory follows a hierarchical invariant manifold traversal (HIMT) process, progressively ascending through low-rank solutions towards a global minimum. This HIMT process, generalizing prior work, elegantly explains the model’s preference for low-rank solutions. Conversely, disconnected data introduces sub-invariant manifolds that hinder convergence to the global minimum, resulting in solutions with suboptimal rank. The interplay between data connectivity and the resulting invariant manifolds profoundly influences the training trajectory and ultimately determines whether the model favors low rank or low nuclear norm, highlighting the intricate relationship between data structure and implicit bias.
Theoretical Analysis#
A theoretical analysis section in a research paper would typically delve into a formal mathematical framework to support the empirical findings. It might involve defining key concepts rigorously, proving theorems related to the model’s behavior (e.g., convergence guarantees, bias characterizations), or analyzing the loss landscape. The depth and complexity would depend heavily on the paper’s specific focus. For example, a study on implicit regularization in matrix factorization might rigorously prove the existence of specific invariant manifolds that constrain the optimization trajectory, linking data connectivity to the model’s implicit bias. It might also involve proving guarantees about the model achieving minimum rank or nuclear norm under certain conditions. The level of mathematical sophistication required would vary; some papers may rely on linear algebra and optimization theory, while others may utilize more advanced concepts from differential geometry or dynamical systems. A strong theoretical analysis would not only solidify the paper’s claims but also offer broader insights into the underlying mechanisms. It’s crucial that the theoretical analysis is tightly connected to the empirical results, providing a cohesive and comprehensive understanding of the problem.
Future Directions#
The future of research in implicit regularization within matrix factorization models holds exciting possibilities. Extending the theoretical analysis to encompass a broader range of architectures beyond matrix factorization, such as deep neural networks, is crucial to establish more generalizable principles. Investigating the interplay between data connectivity and implicit regularization in more complex settings, particularly with noisy or incomplete data, will reveal valuable insights. Developing practical algorithms that leverage the understanding of implicit regularization for improved generalization and efficiency remains a significant goal. Finally, exploring applications in various fields, especially those involving large-scale data, can uncover novel solutions to challenging real-world problems and solidify the practical implications of this research area. The potential for discovering new invariant structures guiding optimization and uncovering further relationships between the training dynamics and implicit regularization remains a rich avenue for exploration.
More visual insights#
More on figures
🔼 This figure shows how data connectivity influences implicit regularization in matrix factorization models for matrix completion. It plots the rank and nuclear norm of solutions obtained from training against the ground truth rank and nuclear norm for various sample sizes and connectivity patterns (connected, disconnected). Darker points represent more experiments at the same condition. The results suggest a transition in the implicit bias from low nuclear norm to low rank as data connectivity increases.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ ]R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)
🔼 This figure shows how the connectivity of observed data influences implicit regularization in matrix factorization models for matrix completion. The x-axis represents the ground truth rank of the matrix, while the y-axis represents the ground truth nuclear norm. Each point represents the results from an experiment with a specific level of data connectivity (connected or disconnected) and number of observations. The results suggest that connected data tends to result in low-rank solutions, while disconnected data results in low-nuclear-norm solutions. The color intensity indicates the number of samples.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)

🔼 This figure shows the impact of data connectivity on implicit regularization in matrix factorization models for matrix completion. It plots the learned rank and nuclear norm against the ground truth values for various sample sizes and data connectivity patterns (connected and disconnected). The results suggest a transition in implicit regularization from low nuclear norm to low rank as data connectivity increases.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ ]R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)
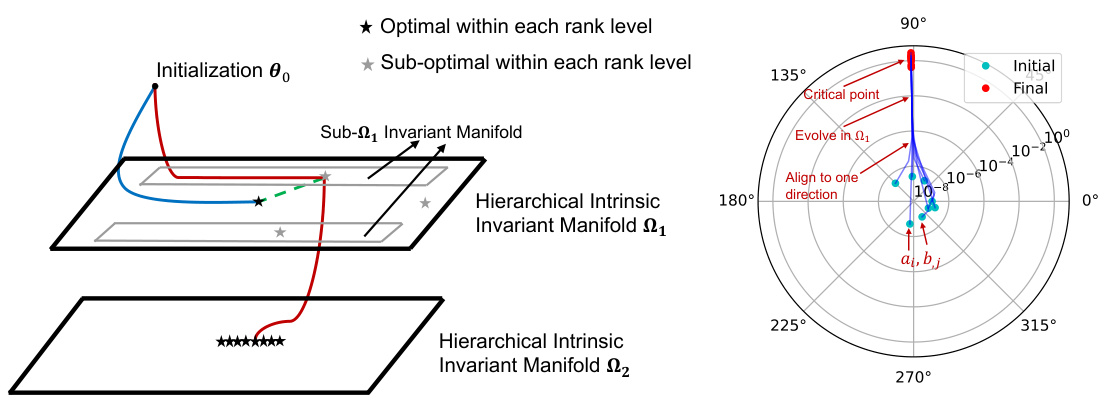
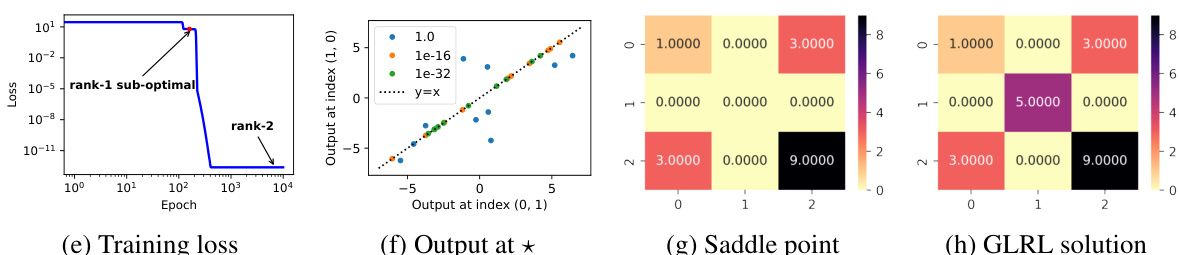
🔼 This figure illustrates the training dynamics in disconnected and connected cases. Panel (a) shows the training trajectory in a disconnected case, highlighting how the model learns a suboptimal solution by traversing through sub-invariant manifolds. Panel (b) displays the parameter alignment during training, demonstrating how the model progressively aligns towards specific directions in parameter space. This alignment is related to a hierarchical intrinsic invariant manifold.
read the caption
Figure 5: (a) Illustrated trajectories for the experiment in Fig. 4. The blue line represents the trajectory converging to the lowest-rank solution, and the red line represents the actual trajectory experienced by the model. (b) The parameter trajectory escaping from a second-order stationary point to reach the next critical point for the experiment in Fig. 3. The 8 scatter points represent the 4 row vectors of matrix A and the 4 column vectors of matrix B. For ease of visualization, we randomly project them onto two dimensions and plot them in polar coordinates.
🔼 This figure shows the impact of data connectivity on implicit regularization in matrix factorization models for matrix completion. The x-axis represents the ground truth rank of the matrix, while the y-axis represents the ground truth nuclear norm. Each point represents a different matrix completion experiment with varying levels of data connectivity (indicated by color and point density), and sample size. The figure demonstrates a transition from low nuclear norm regularization to low rank regularization as the connectivity of observed data increases.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)
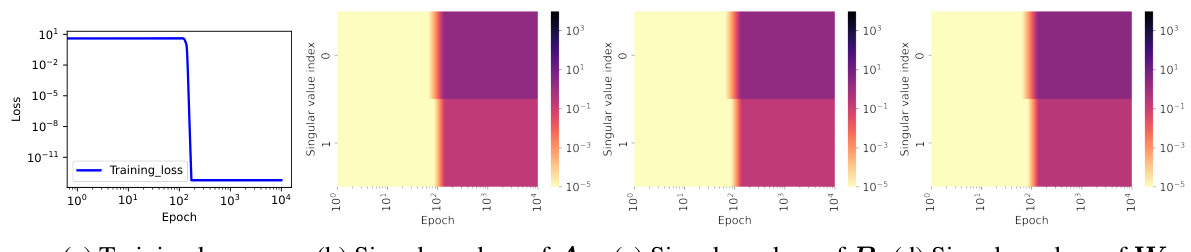
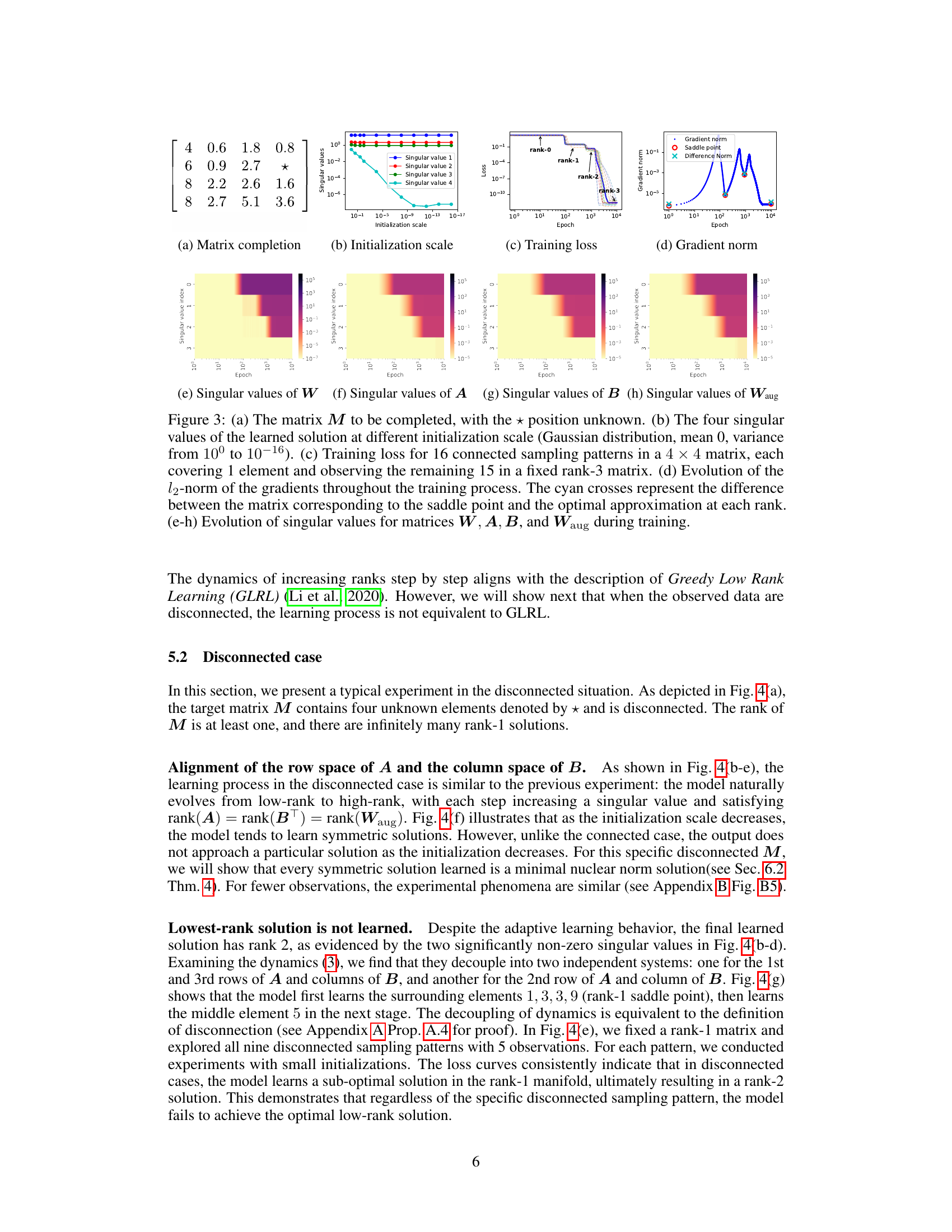
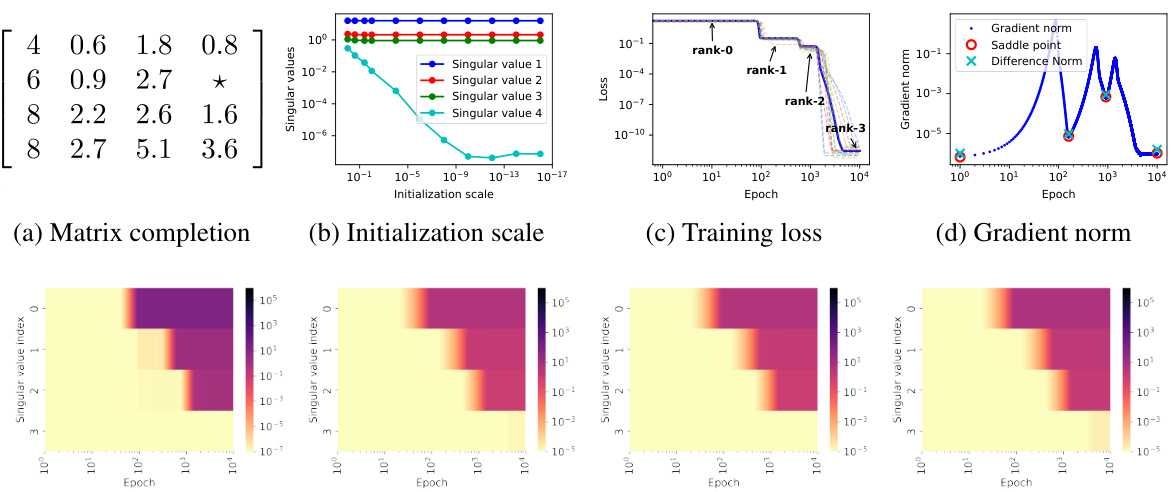
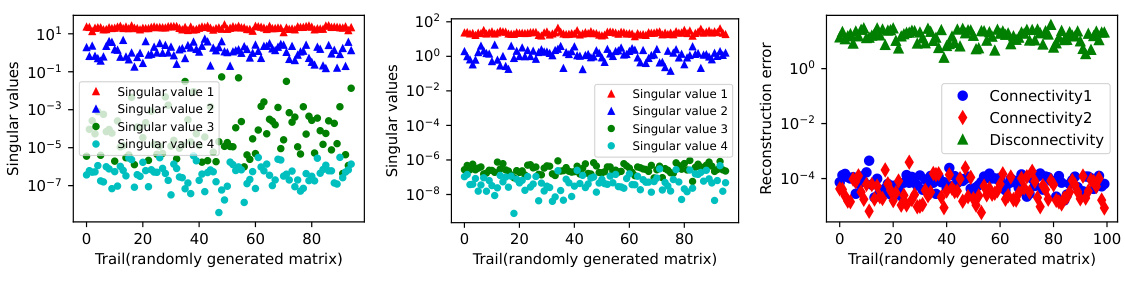
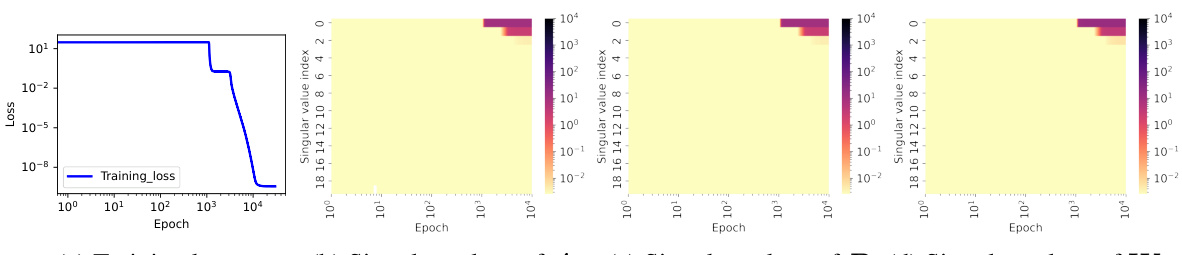
🔼 This figure shows the training dynamics of a connected matrix completion problem. Panel (a) displays the target matrix. Panel (b) illustrates how the learned solution’s rank changes with different initialization scales, showing a transition from rank 4 to rank 3 as the scale decreases. Panel (c) shows the training loss, with flat periods indicating potential saddle points. Panel (d) compares the matrices learned at those points with optimal approximations for each rank. Panels (e-h) track the singular values of several matrices during training, revealing an alignment in their row and column spaces which aligns with the concept of hierarchical intrinsic invariant manifold.
read the caption
Figure 3: (a) The matrix M to be completed, with the position unknown. (b) The four singular values of the learned solution at different initialization scale (Gaussian distribution, mean 0, variance from 10⁰ to 10⁻¹⁶). (c) Training loss for 16 connected sampling patterns in a 4 × 4 matrix, each covering 1 element and observing the remaining 15 in a fixed rank-3 matrix. (d) Evolution of the l²-norm of the gradients throughout the training process. The cyan crosses represent the difference between the matrix corresponding to the saddle point and the optimal approximation at each rank. (e-h) Evolution of singular values for matrices W, A, B, and Waug during training.
🔼 This figure shows how the connectivity of observed data influences implicit regularization in matrix factorization models for matrix completion. Different colors represent different data connectivity patterns (connected, disconnected with complete bipartite components, and other disconnected patterns). The x-axis represents the ground truth rank and nuclear norm, while the y-axis represents the rank and nuclear norm of the learned solutions. The plot demonstrates a transition from low nuclear norm to low rank regularization as data shifts from disconnected to connected with increasing observations. The size of each point indicates the number of samples used.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)

🔼 This figure shows how data connectivity influences implicit regularization in matrix factorization for matrix completion. The x-axis represents the ground truth rank, and the y-axis represents the ground truth nuclear norm. Each point represents the results of a matrix completion experiment with different levels of observed data connectivity and sample size. The color intensity of each point indicates the number of samples used in the experiment. The figure demonstrates a clear transition from low nuclear norm to low rank as data connectivity increases.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)

🔼 This figure shows how the connectivity of observed data impacts implicit regularization in matrix factorization models for matrix completion. It plots the rank and nuclear norm of solutions against the connectivity of the observed data for various sample sizes. The results show a transition from low nuclear norm to low rank solutions as connectivity increases, indicating that data connectivity plays a significant role in shaping the implicit bias of these models. The experiment is repeated to show statistical significance.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ ]R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)
🔼 This figure shows how the connectivity of observed data influences implicit regularization in matrix factorization models for matrix completion. The x-axis represents the rank of the ground truth matrix, and the y-axis represents its nuclear norm. Different colors and shapes of points represent different data connectivity patterns (connected, disconnected with complete bipartite components, or other disconnected patterns). The size of each point corresponds to the number of samples used in the experiment. The plot shows that connected data leads to low-rank solutions while disconnected data often leads to solutions with lower nuclear norm, demonstrating the impact of data connectivity on the implicit bias of matrix factorization models.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)

🔼 This figure shows how the connectivity of observed data influences implicit regularization in matrix factorization models for matrix completion. The x-axis represents the ground truth rank, and the y-axis represents the ground truth nuclear norm of the matrix. Each point represents an experiment, with the color indicating the connectivity of the observed data (connected or disconnected) and the intensity representing the number of samples. The results demonstrate a transition from low nuclear norm regularization to low-rank regularization as data connectivity increases.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ ]R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)
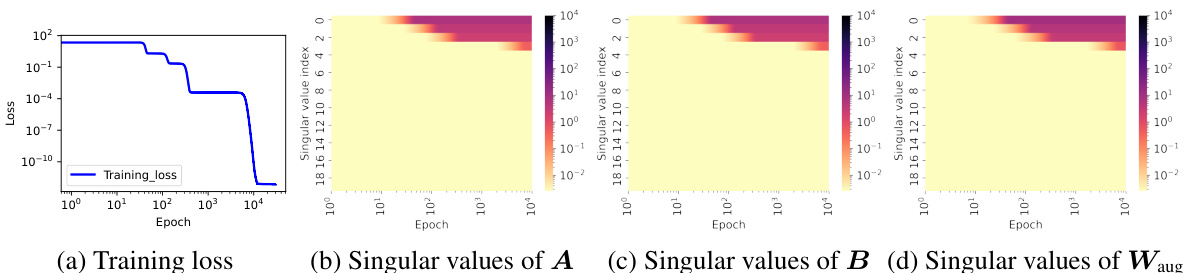
🔼 This figure demonstrates the training dynamics and the results in a disconnected case. Subfigures (b)-(d) show the singular values of A, B, and the augmented matrix Waug during training, indicating that the model progresses from low rank to high rank while maintaining rank(A) = rank(BT) = rank(Waug). Subfigure (e) shows the training loss for various disconnected sampling patterns, revealing that the model fails to achieve the optimal low-rank solution in this case. Subfigure (f) illustrates the learned values at symmetric positions under varying initialization scales, highlighting the existence of infinitely many rank-1 solutions. Subfigure (g) displays the learned output at the saddle point, and subfigure (h) shows the solution obtained using the Greedy Low-Rank Learning (GLRL) algorithm.
read the caption
Figure 4: (a) The matrix to be completed, with unknown entries marked by *. (b-d) Evolution of singular values for A, B, and Waug during training. (e) Training loss for 9 disconnected sampling patterns in a 3 × 3 matrix, each covering 4 elements and observing the remaining 5 in a fixed rank-1 matrix. (f) Learned values at symmetric positions (1, 2) and (2, 1) under varying initialization scales (zero mean, varying variance). Each point represents one of ten random experiments per variance; labels show initialization variance. Other symmetric positions exhibit similar behavior. (g) Learned output at the saddle point corresponding to the red dot in (e). (h) Final learned solution of the GLRL algorithm (Li et al., 2020).

🔼 This figure demonstrates the impact of data connectivity on the implicit regularization in matrix factorization models for matrix completion. It shows how the model’s tendency to favor low-rank solutions increases as the observed data becomes more connected. Different levels of connectivity are tested by varying the number of observed entries and their arrangement in the matrix. The results illustrate a transition from low nuclear norm to low-rank solutions as the connectivity shifts. The experiment is repeated multiple times to ensure reliability.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ ]R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)
🔼 This figure shows the impact of observed data connectivity on implicit regularization in matrix factorization models for matrix completion. It demonstrates a transition from low nuclear norm to low rank solutions as data connectivity increases with the number of observations. The plots illustrate the relationship between the ground truth rank/nuclear norm of the matrix and the rank/nuclear norm obtained by the model under different connectivity conditions and sample sizes.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)
🔼 This figure shows how the connectivity of observed data influences the implicit regularization in matrix factorization models for matrix completion. It demonstrates a transition in implicit bias from low nuclear norm regularization to low rank regularization as the connectivity of the observed data increases. The experiments vary sample size and track the minimum nuclear norm and rank solutions, with darker points representing more samples. The plots show a clear relationship between data connectivity and the implicit regularization effect.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ ]R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)
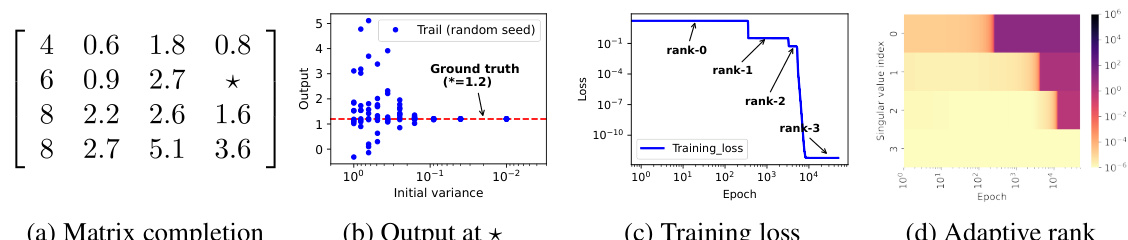
🔼 This figure shows the training dynamics of a connected matrix factorization model. It illustrates how the initialization scale affects the rank of the learned solution, the typical training loss curve, gradient norm evolution, and the alignment between row and column spaces during the learning process. The results support the concept of traversing through progressive optima at each rank and the alignment of row and column spaces.
read the caption
Figure 3: (a) The matrix M to be completed, with the position unknown. (b) The four singular values of the learned solution at different initialization scale (Gaussian distribution, mean 0, variance from 10° to 10-16). (c) Training loss for 16 connected sampling patterns in a 4 × 4 matrix, each covering 1 element and observing the remaining 15 in a fixed rank-3 matrix. (d) Evolution of the 12-norm of the gradients throughout the training process. The cyan crosses represent the difference between the matrix corresponding to the saddle point and the optimal approximation at each rank. (e-h) Evolution of singular values for matrices W, A, B, and Waug during training.

🔼 This figure shows how the connectivity of observed data influences implicit regularization in matrix factorization models for matrix completion. It plots the rank and nuclear norm of solutions against the connectivity of the observed data for different sample sizes. The results demonstrate a transition from low nuclear norm solutions to low-rank solutions as data connectivity increases.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ \(\mathbb{R}\)^{4 \times 4} has rank ranging from 1 to 3. The sample size \(n\) covers settings where \(n\) is equal to, smaller than, and larger than the \(2d^2 - r^2\) threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)

🔼 This figure shows how the connectivity of observed data influences implicit regularization in matrix factorization models for matrix completion. The x-axis represents the ground truth rank, and the y-axis represents the ground truth nuclear norm of the matrix to be completed. The different colored points represent different data connectivity scenarios (connected, disconnected with complete bipartite components, and otherwise disconnected). The size of each point is proportional to the number of samples used in the experiment. The figure demonstrates a transition in implicit regularization from low nuclear norm to low rank as data connectivity increases. More samples are shown as darker points.
read the caption
Figure 1: The connectivity of observed data affects the implicit regularization. The ground truth matrix M* ∈ ]R4×4 has rank ranging from 1 to 3. The sample size n covers settings where n is equal to, smaller than, and larger than the 2rd – r2 threshold required for exact reconstruction. Darker scatter points indicate a greater number of samples, while lighter points indicate fewer samples. The positions of observed entries are randomly chosen, and the experiment is repeated 10 times for each sample size. (Please refer to Appendix B for additional experiments and detailed methodology.)
Full paper#