TL;DR#
Current methods for training LLMs often rely on finetuning with synthetic data generated by powerful models. However, simply using positive examples can lead to overfitting and poor generalization. This paper investigates the use of synthetic data for enhancing LLM math reasoning capabilities. The researchers discovered that this approach leads to only modest gains, and in some cases, even performance degradation.
The study introduces a novel approach that utilizes both positive and negative synthetic data. By carefully constructing negative examples that highlight critical reasoning steps, the researchers achieved significant performance improvements. This method is shown to be equivalent to advantage-weighted reinforcement learning (RL), offering better sample efficiency and generalization compared to relying solely on positive data. This novel strategy demonstrates a significant improvement in LLM performance using a relatively simple technique.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with large language models (LLMs) and synthetic data. It directly addresses the challenges of effective LLM finetuning using synthetic data, a critical area given the limitations of real-world datasets. The findings on the benefits of using negative data alongside positive data, and the novel theoretical framework linking this approach to RL, open up exciting avenues for future research. Improved sample efficiency and robustness of LLM training are significant advancements with broad implications.
Visual Insights#

🔼 This figure illustrates the process of generating positive and negative synthetic data for training large language models (LLMs) on mathematical reasoning tasks. The process begins with reasoning Q&A pairs sampled from a capable model (like GPT-4). These pairs are used to fine-tune a base model (such as Llama-2) using Supervised Fine-Tuning (SFT), resulting in an SFT model. This SFT model is then used to generate both positive (correct) and negative (incorrect) responses to the same questions. The positive responses are used to further fine-tune the base model using Rejection Fine-Tuning (RFT), resulting in an RFT model. The negative responses are filtered by calculating a per-step credit (measuring the impact of each step in the solution trace). These filtered negative responses, along with the positive responses from the initial capable model, are used to fine-tune the SFT model using a per-step Direct Preference Optimization (DPO) approach, resulting in a per-step DPO model. The figure visually represents the flow of data and the different training methods used.
read the caption
Figure 1: Positive and negative synthetic data: Pictorial representation of positive/negative synthetic data definitions we use and how they are fed to SFT, RFT and DPO.

🔼 The figure compares the performance of training LLMs on two types of synthetic data for math reasoning. The first is data generated from larger, more capable models (SFT data), and the second is data generated by the learner itself (RFT data). Both datasets contain the same number of problems, but the RFT data only has one correct solution per problem, while the SFT data has multiple. Despite this difference, the results indicate that the RFT data results in better performance.
read the caption
Figure 9: RFT data with a single (self-generated) correct solution per problem outperforms SFT data (from highly-capable models) of the same size.
In-depth insights#
Synthetic Data Scaling#
The study’s exploration of synthetic data scaling reveals interesting complexities. While scaling positive synthetic data from capable models initially improves performance, the gains diminish significantly, indicating a plateauing effect. Surprisingly, self-generated positive data from the learner itself proves surprisingly effective, even doubling efficiency compared to external sources. However, reliance solely on positive data amplifies spurious correlations, potentially leading to performance stagnation or even decline. This is because the models can overfit on irrelevant details in the solution, which are not detected by final answer verifiers. Critically, the inclusion of carefully constructed negative data drastically alters the scaling trajectory, resulting in consistent gains far exceeding the improvements observed with just positive data. This suggests that negative data helps to correct spurious correlations by emphasizing critical steps in problem-solving. Overall, the findings highlight the importance of a balanced approach when utilizing synthetic data, emphasizing both the advantages and drawbacks of scaling different types of synthetic data. The conceptual link between the use of negative data and advantage-weighted reinforcement learning is a key theoretical contribution This helps explain why carefully selected negatives prove to be so beneficial.
Negative Data Benefits#
The concept of leveraging ’negative data’ – incorrect or suboptimal model-generated responses – for improving model performance is particularly insightful. It addresses the limitations of solely relying on positive examples, which can lead to overfitting on spurious correlations and hinder generalization. By carefully constructing negative data that emphasizes critical intermediate steps in the problem-solving process, models can learn to differentiate between good and bad choices at crucial junctures, significantly improving sample efficiency. This approach is akin to advantage-weighted reinforcement learning, offering benefits in terms of robustness and generalization. The study’s finding that negative data can deliver performance gains equivalent to increasing the positive dataset size eightfold is particularly noteworthy. However, careful negative data construction is paramount. Arbitrarily contrasting correct and incorrect responses is less effective. The strategic construction of negatives, focused on critical steps and highlighting crucial decision points, is key to unlocking the significant benefits of incorporating negative data in model training.
RL Connection#
The heading ‘RL Connection’ suggests an exploration of the relationship between reinforcement learning (RL) and another topic within the research paper. A thoughtful analysis would delve into how RL principles, algorithms, or methodologies are applied, adapted, or compared. The core idea may involve using RL to optimize a model, improve efficiency, or address specific challenges. The discussion likely demonstrates how RL’s ability to learn through trial and error, reward feedback, and policy optimization translates to solving problems in the study’s domain. This could mean that the research uses RL for training, evaluation, or both, potentially highlighting how RL techniques outperform alternative approaches. A key aspect would be the explanation of how the RL framework is incorporated, including the choice of reward function, environment setup, and algorithm selection. There might be a comparison of RL-based methods with other techniques, such as supervised learning or imitation learning, to quantify its effectiveness. Finally, the analysis should consider any limitations or novel adaptations of RL methods employed in the research.
Spurious Correlation#
The concept of “spurious correlation” is central to understanding the challenges of training large language models (LLMs) on synthetic data. Spurious correlations arise when the model learns relationships between variables in the training data that don’t reflect true causal relationships in the real world. In the context of math problem-solving, this means the model might learn to associate specific intermediate steps or patterns with a correct answer, even if those steps are logically flawed or irrelevant. This phenomenon is amplified when training predominantly on positive examples (correct solutions), leading to overfitting on these superficial patterns. The authors highlight the need to carefully design negative examples (incorrect solutions) to counteract spurious correlations. Simply presenting incorrect answers isn’t enough; negatives must highlight precisely where the model’s reasoning deviates from a correct path to be effective. By incorporating well-constructed negative examples, the model can learn to avoid spurious correlations and improve its generalization performance on unseen problems. This approach resembles advantage-weighted reinforcement learning, suggesting a theoretical foundation for the effectiveness of this technique.
Future Work#
Future research directions stemming from this paper could explore several avenues. Extending the methodology to other complex reasoning tasks beyond mathematics would demonstrate the generalizability of using negative synthetic data for improved LLM performance. Investigating the optimal strategies for constructing negative examples is crucial; exploring alternative methods for identifying critical steps and weighting negative samples could enhance performance. A deeper theoretical analysis is warranted, potentially moving beyond the current advantage-weighted RL framework to establish a more fundamental understanding of how negative data impacts learning and generalisation. Finally, empirical studies examining the impact of dataset size and model scale on the effectiveness of negative data would provide valuable insights into the practical applicability and scalability of this technique. The interplay between positive and negative data should be studied more thoroughly. Determining the optimal ratio of positive to negative samples or exploring more sophisticated data sampling strategies could further refine the approach.
More visual insights#
More on figures
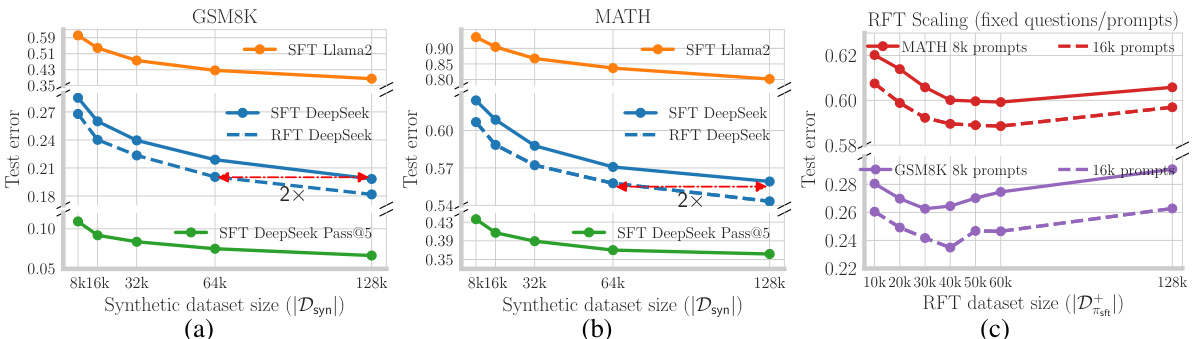
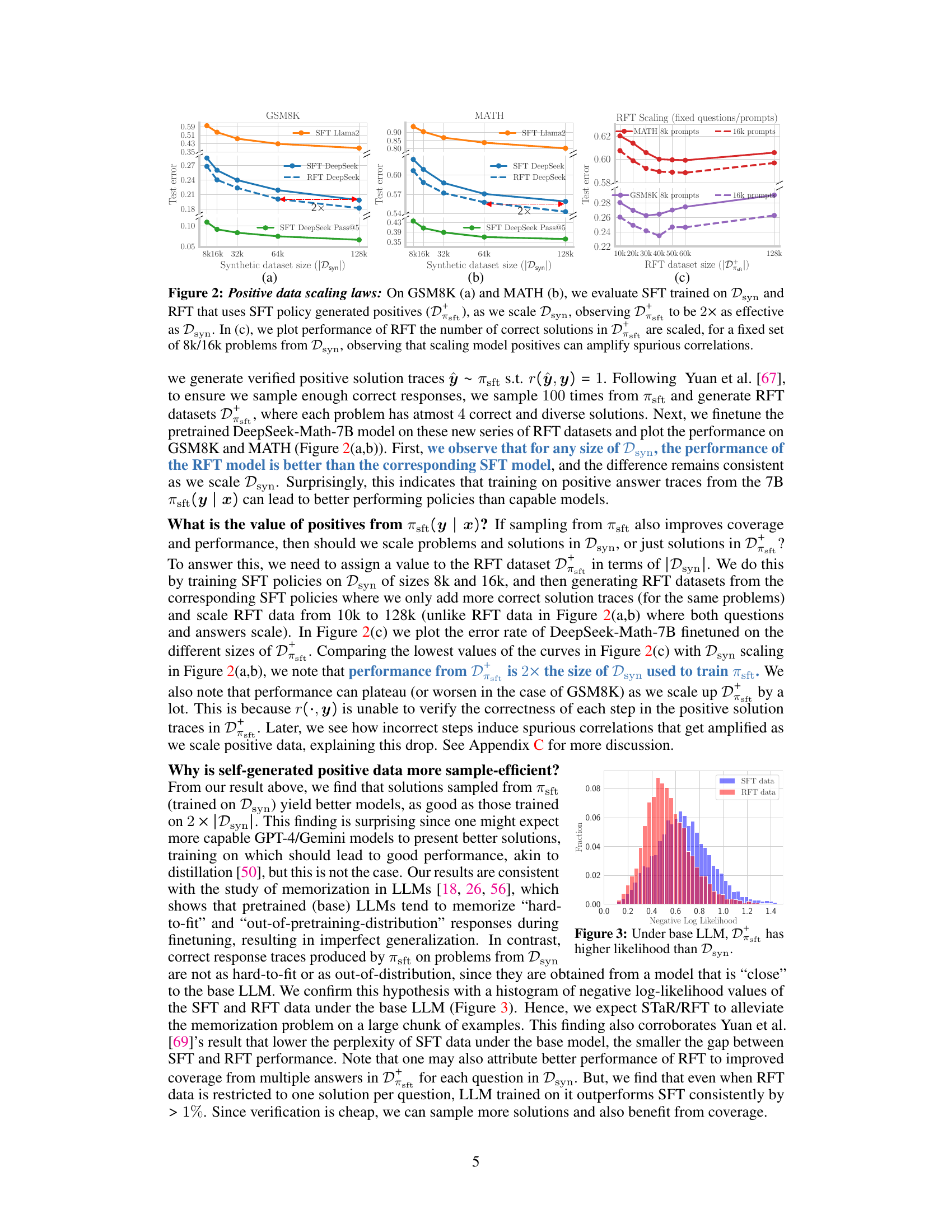
🔼 This figure shows the scaling laws of positive synthetic data for both GSM8K and MATH datasets. It compares the performance of Supervised Fine-tuning (SFT) and Rejection Fine-tuning (RFT) as the size of the synthetic dataset increases. Panel (a) and (b) show that RFT using self-generated positive data is twice as effective as using synthetic data from larger models. Panel (c) demonstrates that scaling model-generated positive data can lead to amplified spurious correlations, resulting in performance plateaus or even degradation.
read the caption
Figure 2: Positive data scaling laws: On GSM8K (a) and MATH (b), we evaluate SFT trained on Dsyn and RFT that uses SFT policy generated positives (Draft), as we scale Dsyn, observing D+ to be 2x as effective as Dsyn. In (c), we plot performance of RFT the number of correct solutions in D+ are scaled, for a fixed set of 8k/16k problems from Dsyn, observing that scaling model positives can amplify spurious correlations.
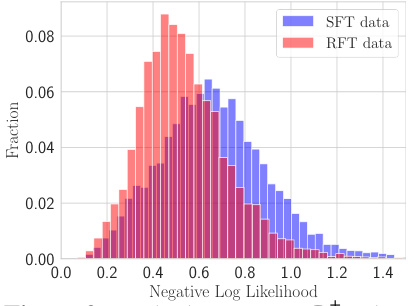
🔼 This figure shows the negative log-likelihood distributions of SFT data (D+sft) and RFT data (Dsyn) under the base language model (LLM). The distribution of RFT data is shifted to the left compared to SFT data. This means the RFT data (positive responses from the 7B model) is easier to predict by the base LLM compared to the SFT data (responses from more capable models). The observation supports that the responses from the similar model are easier-to-fit than those from more capable models, resulting in reduced memorization during finetuning.
read the caption
Figure 3: Under base LLM, D+sft has higher likelihood than Dsyn.
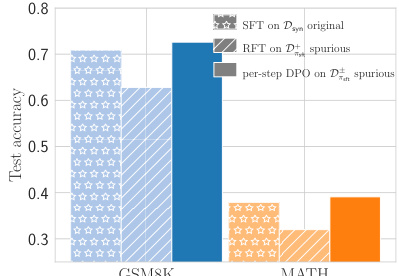
🔼 This figure shows that spurious correlations in the RFT (Rejection Finetuning) data can negatively impact model performance. The SFT (Supervised Finetuning) model trained on original synthetic data achieves relatively high test accuracy on both GSM8K and MATH datasets. However, when spurious correlations are introduced into the RFT data, the performance drops significantly, highlighting the detrimental effect of such correlations.
read the caption
Figure 4: Spurious correlations in RFT data hurt performance.

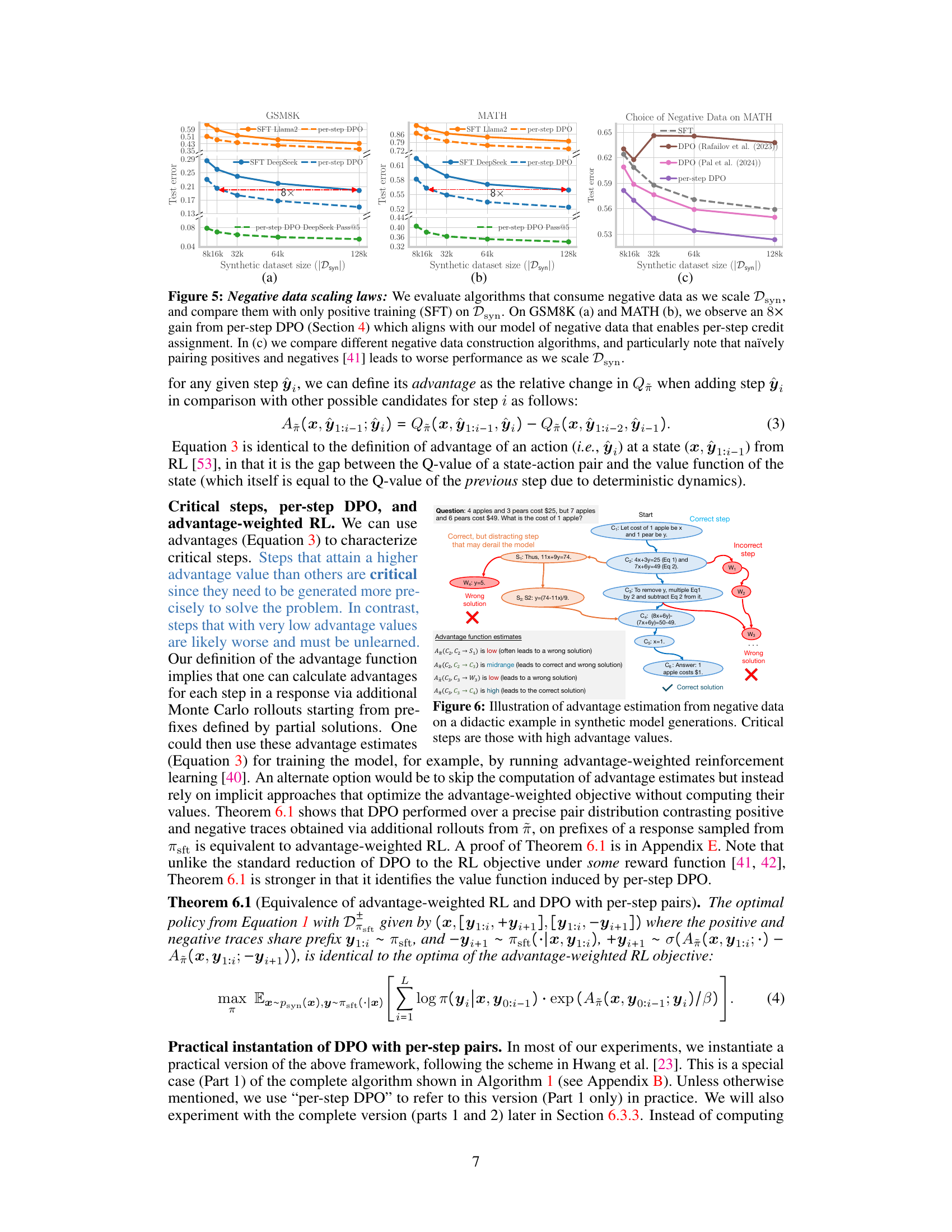
🔼 This figure demonstrates the scaling laws observed when training LLMs with negative synthetic data, showing a significant performance improvement (8x) using the per-step DPO method compared to using only positive data. It also highlights the importance of constructing negative data appropriately, as naive methods can lead to worse performance.
read the caption
Figure 5: Negative data scaling laws: We evaluate algorithms that consume negative data as we scale Dsyn, and compare them with only positive training (SFT) on Dsyn. On GSM8K (a) and MATH (b), we observe an 8× gain from per-step DPO (Section 4) which aligns with our model of negative data that enables per-step credit assignment. In (c) we compare different negative data construction algorithms, and particularly note that naïvely pairing positives and negatives [41] leads to worse performance as we scale Dsyn.
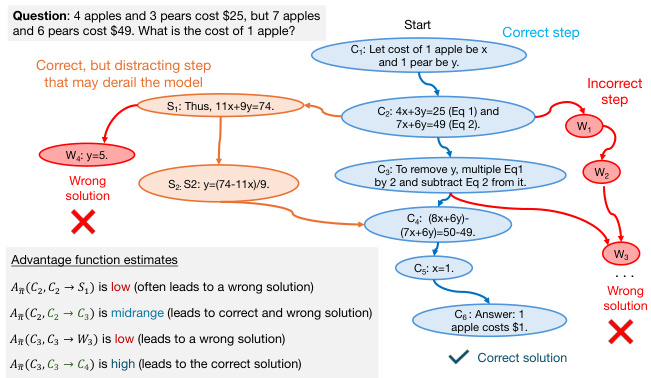
🔼 This figure illustrates the process of generating and utilizing both positive and negative synthetic data for training language models. Positive data consists of question-answer pairs with correct solutions, generated either by a capable model (e.g., GPT-4) or self-generated by the model being trained. Negative data consists of model-generated answers deemed incorrect by a verifier, where the construction of negatives emphasizes ‘critical’ steps in the reasoning process. The figure shows how these positive and negative data points are fed into three different finetuning methods: Supervised Fine-tuning (SFT), Rejection Fine-tuning (RFT), and Direct Preference Optimization (DPO). The arrows indicate the flow of data and the finetuning process.
read the caption
Figure 1: Positive and negative synthetic data: Pictorial representation of positive/negative synthetic data definitions we use and how they are fed to SFT, RFT and DPO.

🔼 This figure shows the average Q-values at each step for different negative data schemes. The x-axis represents the step number, and the y-axis represents the average Q-value. The lines represent different methods for incorporating negative data: SFT (supervised fine-tuning), DPO (Rafailov et al., 2023), DPO (Pal et al., 2024), and per-step DPO. The figure demonstrates that per-step DPO improves Q-values at each step, while standard DPO only shows improvement in irrelevant steps. This highlights the advantage of per-step DPO in focusing on critical steps during training.
read the caption
Figure 7: Per-step DPO improves Q-values at each step, standard DPO only improves at irrelevant steps.

🔼 This figure shows the results of a didactic analysis on a star graph problem, comparing the performance of standard SFT and per-step DPO. It demonstrates how per-step DPO addresses the memorization problem present in SFT by focusing on critical steps in the reasoning process. The plots visualize the training loss, Q-values of the critical token, and test error, highlighting the effectiveness of per-step DPO, especially when starting from under-trained models.
read the caption
Figure 8: Didactic analysis on star graph: In (a) we plot the SFT loss and Q-value of the critical token (adjacent node) for SFT and per-step DPO (starting from iter 60). Indicative of memorization SFT loss decreases at a slow rate, matching the slow rate of increase in the Q-value. In contrast per-step DPO loss sharply decreases during training. In (b) we notice a corresponding phase transition in the test error of per-step DPO starting from different under-trained SFT checkpoints, which does not happen for an over-trained SFT checkpoint in (c).

🔼 The figure shows that using RFT (Rejection finetuning) with self-generated data improves model performance compared to using SFT (Supervised finetuning) data from larger models. Even with only one correct solution per problem from the RFT method, performance is better than using the same number of samples from the larger model’s SFT data. This indicates that self-generated RFT data is more sample-efficient than external SFT data for improving performance.
read the caption
Figure 9: RFT data with a single (self-generated) correct solution per problem outperforms SFT data (from highly-capable models) of the same size.
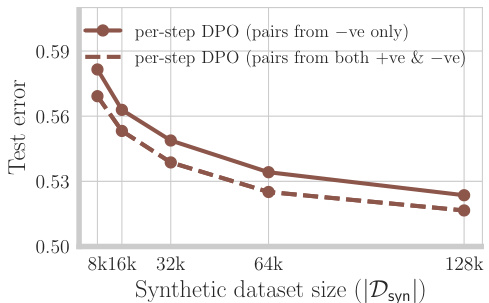
🔼 This figure shows the results of an experiment on the MATH dataset comparing two variants of per-step DPO. The first uses only negative data, while the second uses both positive and negative data for computing advantage estimates. The results demonstrate that using both positive and negative data improves performance, especially as the size of the synthetic dataset increases. This is because using both types of data leads to more accurate advantage estimates, which is crucial for the effectiveness of per-step DPO.
read the caption
Figure 10: On MATH, improving advantage estimates by computing advantages over both positive and negative traces sampled from πsft improves estimation error and final performance for per-step DPO.
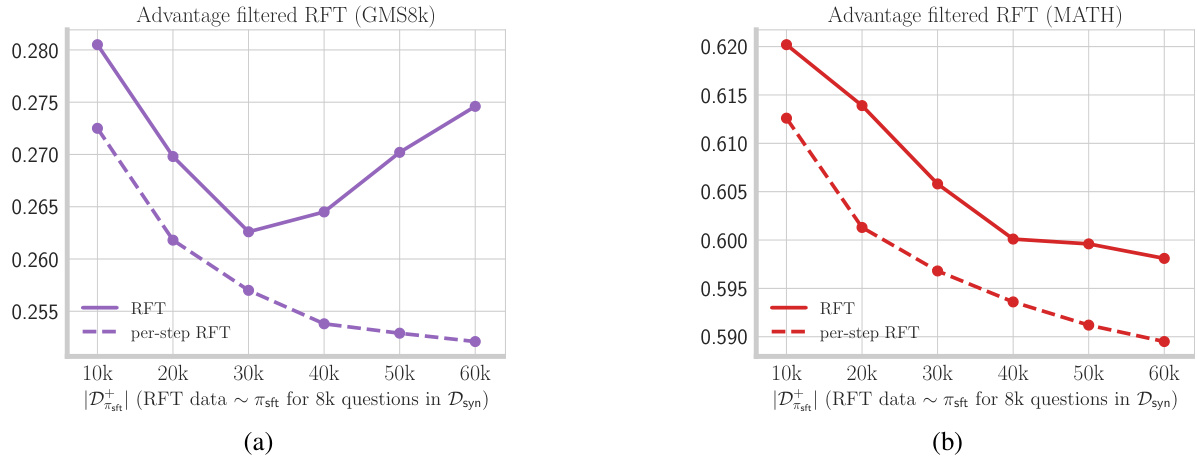
🔼 The figure shows two plots: one for the GSM8K dataset and one for the MATH dataset. Each plot displays the test error rate for RFT and per-step RFT models, as the size of the RFT dataset increases. Advantage filtering is applied, meaning only responses with high advantage steps are included in the training data. The per-step RFT consistently outperforms standard RFT, especially as the dataset size grows, demonstrating the benefit of incorporating per-step advantage information in the training process.
read the caption
Figure 11: Advantage filtered RFT: We clone responses with high advantage steps from positive and negative responses sampled from the SFT policy. We filter all responses where the minimum advantage across all steps is in the bottom 50% percentile.
Full paper#