TL;DR#
Many AI models, even with high test accuracy, don’t meet real-world requirements due to biases in training data and underspecified learning pipelines. Current post-training alignment methods are often limited to generative models. This paper introduces a new post-processing strategy to tackle model misalignment.
The proposed method uses property testing to define model alignment and leverages conformal risk control for post-processing. It maps property tests to loss functions used within a conformal risk algorithm, providing a probabilistic guarantee that the aligned model (or a model within a specific range of the original) satisfies the desired properties. The approach demonstrates practical application on several datasets with shape-constrained properties such as monotonicity and concavity, showcasing flexibility and broader applicability.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the prevalent issue of AI model misalignment, offering a novel post-processing technique to enhance alignment. It’s especially relevant given the rise of large foundation models and addresses the challenge of achieving alignment even with increased data and model size. The method’s flexibility and wide applicability to various properties open up new research avenues in ensuring AI systems are reliable and safe.
Visual Insights#

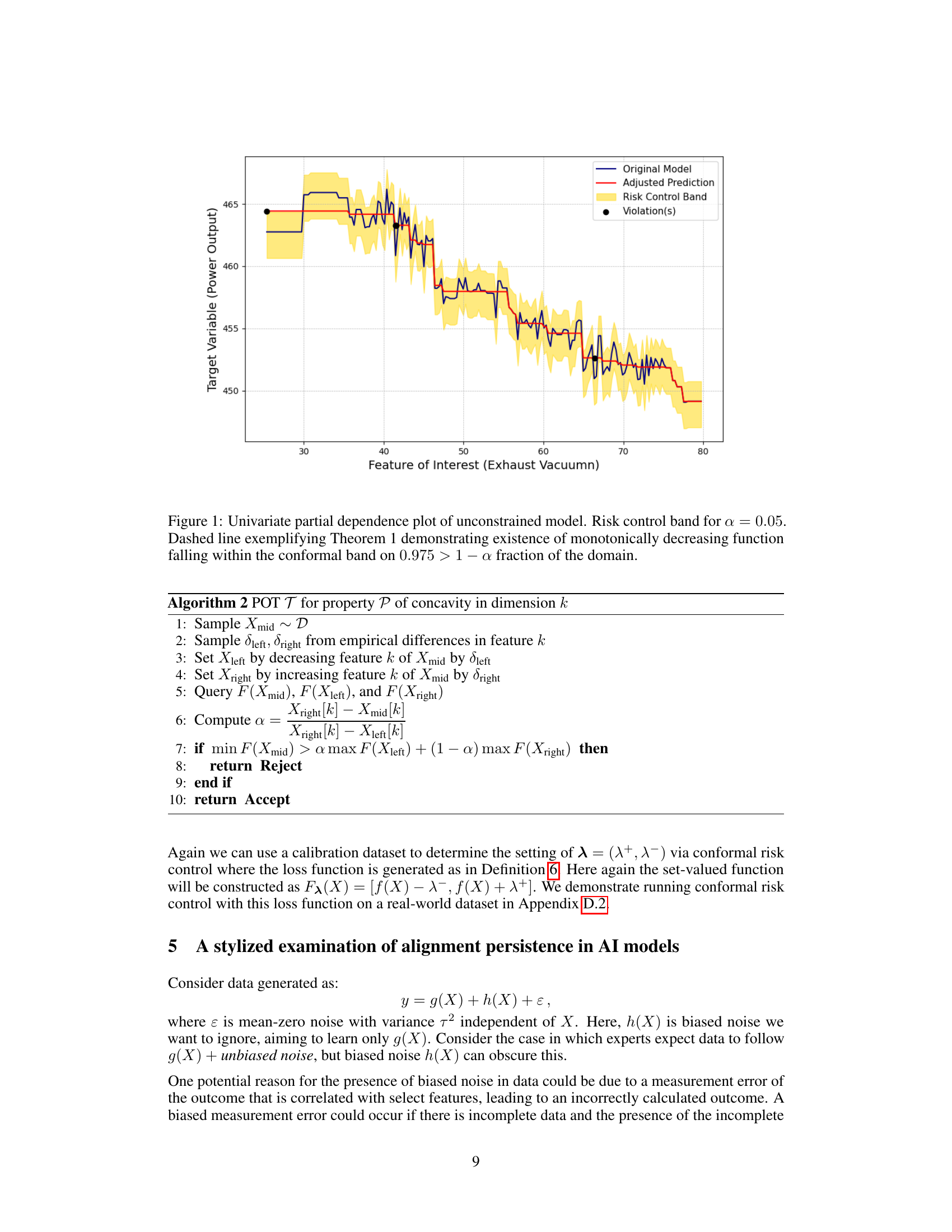
🔼 This figure shows the partial dependence plot of an unconstrained model’s predictions on the ‘Exhaust Vacuum’ feature against the ‘Power Output’ target variable. A conformal risk control band (at α=0.05) is overlaid, representing the range of predictions that maintain a certain level of statistical guarantee. The red line represents adjusted predictions after applying the conformal risk control methodology, aimed at aligning the model’s output with a desired monotonically decreasing property. The dashed line highlights a portion of the data where a monotonically decreasing function exists within the confidence band, as supported by Theorem 1.
read the caption
Figure 1: Univariate partial dependence plot of unconstrained model. Risk control band for α = 0.05. Dashed line exemplifying Theorem 1 demonstrating existence of monotonically decreasing function falling within the conformal band on 0.975 > 1−α fraction of the domain.

🔼 This table presents the results of applying the conformal risk control method to an unconstrained model and compares its performance to a constrained model that satisfies monotonicity in the specified feature (Exhaust Vacuum). It shows the Mean Squared Error (MSE) and risk for different values of alpha (α), and also lists the values of lambda plus (λ+) and lambda minus (λ-), which parameterize the conservativeness of prediction intervals produced by the risk control method. The results demonstrate how controlling the risk affects the trade-off between accuracy and the desired property of monotonicity.
read the caption
Table 1: Power Plant, n = 9568. Monotonically decreasing on Exhaust Vacuum. Amax = (10, 10).
In-depth insights#
Model Alignment#
Model alignment, a critical issue in AI safety, focuses on ensuring that AI systems’ behavior aligns with human values and intentions. The paper tackles this challenge by framing alignment as a property testing problem. Instead of directly training models to exhibit desired properties, it proposes a post-processing technique using conformal risk control. This allows for aligning pre-trained models with specific desirable behaviors without the need for computationally expensive retraining. The core idea is to map property testing queries into loss functions for conformal risk control, creating conformal intervals that, with a probabilistic guarantee, contain a function meeting the desired criteria. This novel approach addresses the limitations of existing human-feedback based alignment methods by being applicable to a broader range of AI models, including those with non-generative outputs. The effectiveness of this methodology is demonstrated through real-world examples focusing on shape-constrained properties like monotonicity and concavity. A further contribution of the paper is a theoretical analysis demonstrating the inherent persistence of the alignment problem, even with increasing model size and training data, in the presence of biases. This underlines the importance of post-processing alignment techniques for ensuring the safe and reliable deployment of AI systems.
Conformal Control#
Conformal control, in the context of machine learning, is a powerful post-processing technique for aligning model predictions with desired properties, such as monotonicity or concavity. It leverages conformal prediction to construct prediction intervals that, with high probability, contain functions satisfying the specified property. This approach addresses the limitations of traditional model training, which struggles to directly enforce such constraints. By working on the output of a pre-trained model, it avoids the computationally expensive retraining process. Furthermore, it provides a theoretical probabilistic guarantee that the aligned model will approximately satisfy the target property. The key innovation lies in transforming property testing queries into suitable loss functions that drive the conformal risk control procedure. This flexible framework offers a general-purpose methodology for alignment, enabling adaptation to various properties and model types.
Property Testing#
Property testing offers a potent framework for verifying whether a large object, such as a function or a graph, satisfies a given property efficiently. Instead of exhaustive analysis, it leverages randomized sampling and local queries to determine with high probability whether the object possesses the property or is significantly different from those that do. One-sided error testers, guaranteeing acceptance of objects satisfying the property, are particularly valuable. The concept of proximity-oblivious testers (POTs) further enhances efficiency by decoupling the testing procedure from the exact distance of the object from the property, enabling adaptable testing strategies. Both adaptive and non-adaptive testing strategies are employed, with the choice influenced by factors such as complexity and available resources. The application of property testing, particularly in the context of aligned AI models, presents a novel approach to model alignment, providing guarantees on model adherence to desired properties without the need for complete retraining, thereby offering significant computational advantages. The field’s flexibility allows its application to a wide variety of properties and models, and the development of efficient testing algorithms is ongoing.
Empirical Results#
The Empirical Results section of a research paper should present findings in a clear, concise, and well-organized manner. It’s crucial to focus on the key metrics used to evaluate the research question and provide sufficient detail about the experimental setup to allow for replication. This section should clearly state whether the results support the hypotheses or claims made in the paper, and it should also discuss any unexpected or surprising findings. Furthermore, it’s critical to include error bars or statistical measures of significance to demonstrate the reliability of the results and their level of statistical certainty. A robust Empirical Results section will also consider the limitations of the methods and findings, acknowledging any potential biases or sources of error that could impact the interpretation of the results. Visualizations such as tables and graphs are often essential to presenting the data in a way that is easily understood, thereby allowing readers to readily grasp the results and their implications.
Future Work#
The paper’s conclusion section on future work highlights several promising avenues for extending the research. Expanding the methodology to a broader range of properties is crucial, moving beyond monotonicity and concavity to encompass other crucial alignment goals. Investigating the sample complexity of property testing algorithms is vital for practical applications and determining whether adaptive querying strategies would improve efficiency. The authors also suggest exploring applications in reinforcement learning (RL) settings, using the approach to define policy functions that satisfy safety constraints. This would require careful consideration of how the framework interacts with the complexities of RL and its inherent uncertainty. Finally, establishing rigorous theoretical guarantees, such as bounds on the probability of misalignment, would significantly enhance the trustworthiness and reliability of the proposed alignment techniques. This could involve further investigation of the relationships between property testing and conformal risk control. Essentially, future work needs to move toward broader applicability, greater efficiency, and a more robust theoretical foundation.
More visual insights#
More on figures

🔼 This figure shows the partial dependence plot of an unconstrained model’s prediction on a single feature. A conformal risk control band is overlaid at a significance level of α = 0.05, indicating a range within which, with 95% probability, there exists a monotonically decreasing function. The dashed line highlights that this monotonically decreasing function is present within the confidence band for a significant portion of the feature’s range, illustrating the effectiveness of the proposed conformal risk control method in aligning model predictions with the desired property.
read the caption
Figure 2: Univariate partial dependence plot of unconstrained model. Risk control band for α = 0.05. Dashed line exemplifying Theorem 1 demonstrating existence of monotonically decreasing function falling within the conformal band on 0.975 > 1 − α fraction of the domain.
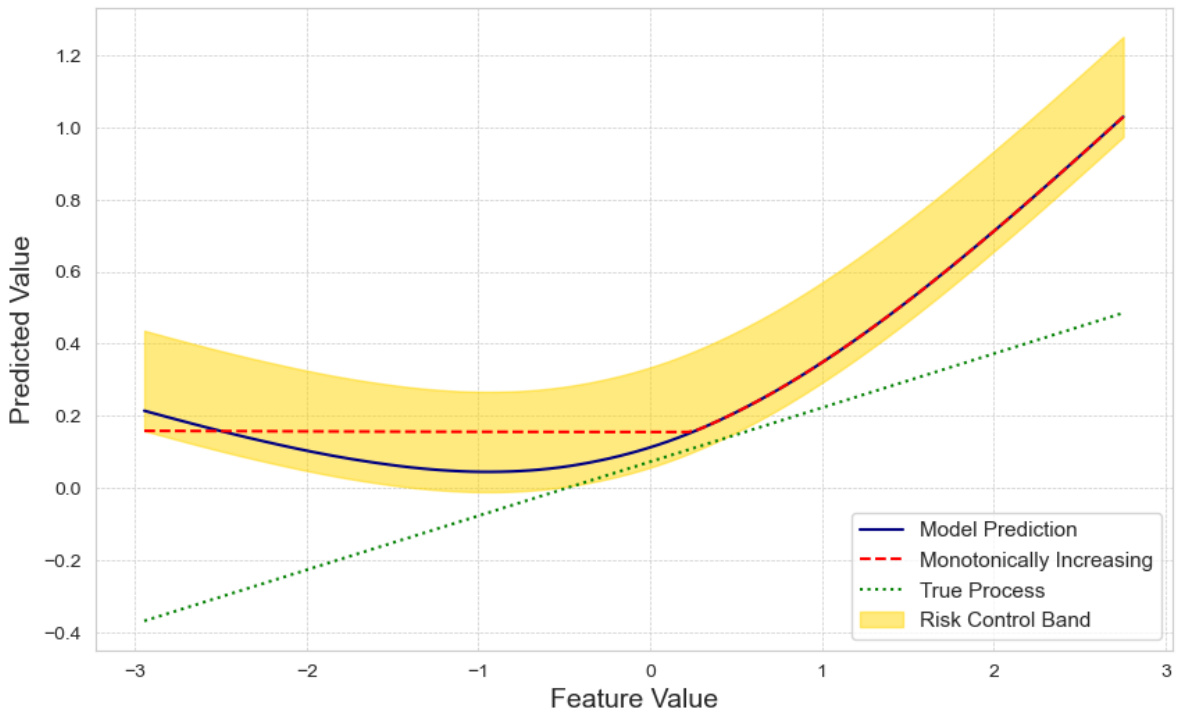
🔼 This figure shows the result of a simulation using a random feature model with 5000 hidden nodes. It depicts the model’s prediction (blue line), a monotonically increasing function (red dashed line) representing the desired behavior, the true underlying process (green dotted line), and the risk control band (yellow shaded area). The plot demonstrates that with a high-complexity model (large N), even with a large dataset, the model may not inherently produce a monotonically increasing prediction without additional alignment techniques. The yellow band shows the interval in which, with high probability, there exists a monotonically increasing function.
read the caption
Figure 3: Random Feature model (N=5000).
More on tables
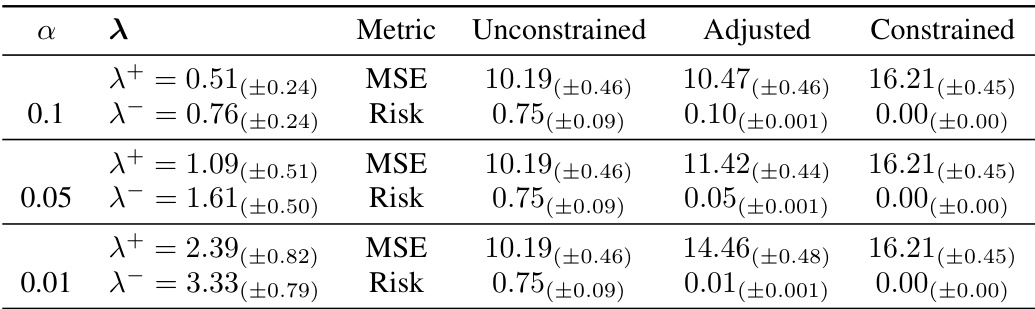
🔼 This table presents the results of applying conformal risk control for enforcing monotonicity on the ‘Exhaust Vacuum’ feature of the Combined Cycle Power Plant dataset. It compares the performance of an unconstrained model, an adjusted model using conformal risk control, and a constrained model (trained with monotonicity constraints). The metrics shown are Mean Squared Error (MSE) and Risk, for different values of the significance level (α). The results demonstrate the effectiveness of conformal risk control in aligning model predictions with the desired monotonicity property, achieving near-perfect alignment with the constrained model for smaller α values.
read the caption
Table 1: Power Plant, n = 9568. Monotonically decreasing on Exhaust Vacuum. Amax = (10, 10).

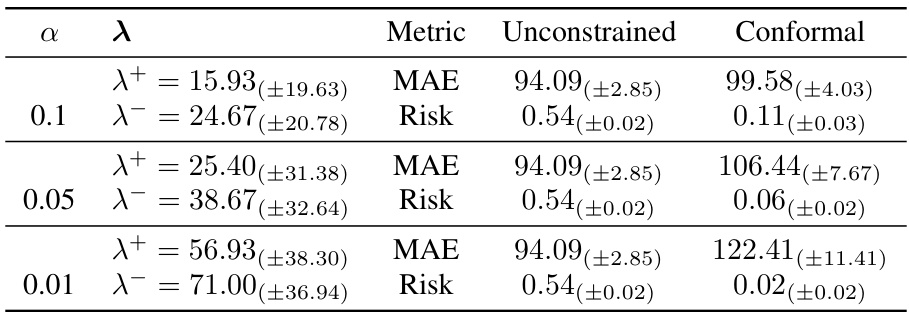
🔼 This table presents the results of applying the conformal alignment procedure for monotonicity on the Abalone dataset. It shows the Mean Squared Error (MSE) and risk for an unconstrained model, an adjusted model (using conformal risk control), and a constrained model (trained with monotonicity constraints). The results are shown for different values of alpha (α), which controls the risk level, and the corresponding optimal lambda values (λ+ and λ−). The constrained model serves as an oracle benchmark, representing the best-case scenario where monotonicity is enforced during training.
read the caption
Table 2: Abalone, n = 4177. Monotonically increasing on Shell_weight. Amax = (5, 5).

🔼 This table presents the results of applying the conformal alignment procedure for monotonicity on the Concrete dataset. It shows the mean squared error (MSE) and risk for an unconstrained model, an adjusted model using conformal risk control, and a constrained model trained with monotonicity constraints. The results are shown for different values of the risk parameter α (0.1, 0.05, and 0.01). The λ+ and λ− values represent the parameters learned during conformal risk control.
read the caption
Table 3: Concrete, n = 1030. Monotonically increasing on Cement. Amax = (2, 2).
🔼 This table presents the results of applying the conformal alignment procedure for monotonicity on the Combined Cycle Power Plant dataset. It compares the performance of unconstrained and constrained models (the latter trained to be monotonically decreasing), as well as a model post-processed using conformal risk control. The metrics shown are Mean Squared Error (MSE) and Risk, for different values of the risk parameter α and the corresponding values of the tuning parameters λ+ and λ-. The constrained model serves as a benchmark representing perfect alignment.
read the caption
Table 1: Power Plant, n = 9568. Monotonically decreasing on Exhaust Vacuum. Amax = (10, 10).
Full paper#