TL;DR#
Offline reinforcement learning (RL) struggles when real-world environments deviate from training data. Robust offline RL aims to solve this by learning policies that perform well under various environmental conditions. However, introducing uncertainty adds nonlinearity and computational complexity, especially when using function approximation techniques to handle large state-action spaces. This study focused on a linear model setting where both nominal and perturbed environments are linearly parameterized, which allows for efficient computations while maintaining robust performance.
The researchers propose two novel algorithms: Distributionally Robust Pessimistic Value Iteration (DRPVI) and its variance-aware variant (VA-DRPVI). These algorithms leverage a novel function approximation mechanism incorporating variance information and instance-dependent suboptimality analysis to achieve a minimax-optimal solution. The algorithms’ efficiency is demonstrated, and theoretical guarantees are provided. A new information-theoretic lower bound shows the algorithms are near-optimal.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in offline reinforcement learning because it tackles the critical challenge of robust policy training under model uncertainty using function approximation. It provides computationally efficient algorithms with theoretical guarantees, advancing the field by establishing instance-dependent suboptimality bounds and a novel information-theoretic lower bound. This work opens avenues for future research in variance-aware methods and handling complex uncertainty sets.
Visual Insights#
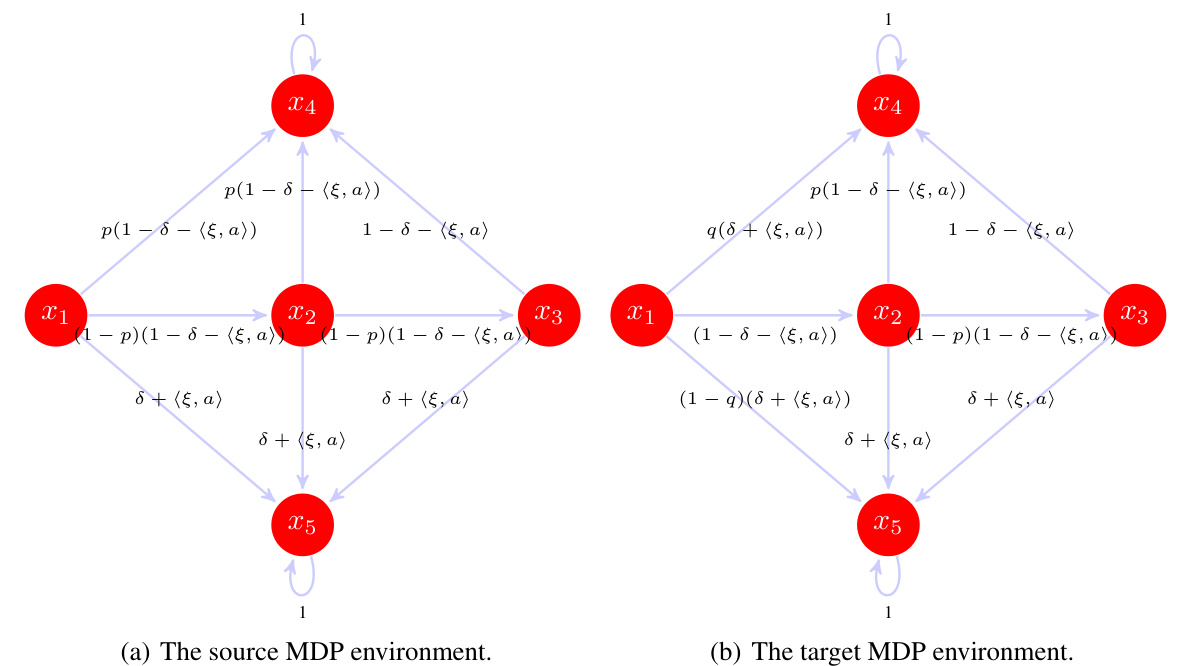
🔼 This figure shows two Markov Decision Processes (MDPs). The source MDP (a) has five states (x1, x2, x3, x4, x5) and three steps. The initial state is x1, state x4 is a ‘fail’ state with reward 0 and state x5 is an absorbing state with reward 1. The target MDP (b) is a modified version of the source MDP, created by changing the transition probabilities from the initial state x1.
read the caption
Figure 1: The source and the target linear MDP environments. The value on each arrow represents the transition probability. For the source MDP, there are five states and three steps, with the initial state being x1, the fail state being x4, and x5 being an absorbing state with reward 1. The target MDP on the right is obtained by perturbing the transition probability at the first step of the source MDP, with others remaining the same.

🔼 This table summarizes the instance-dependent upper bounds on the suboptimality gap achieved by several offline reinforcement learning algorithms with linear function approximation. It compares the results of three algorithms in the standard Markov Decision Process (MDP) setting and two novel algorithms (DRPVI and VA-DRPVI) proposed in the paper for the distributionally robust Markov Decision Process (DRMDP) setting. The algorithms are compared based on the suboptimality gap, which quantifies the difference between the value function of the learned policy and the optimal robust value function. The table highlights the key differences in the upper bound achieved by each algorithm and the settings under which they are applicable. Notably, the results for DRMDP algorithms reveal the impact of considering model uncertainty on the computational complexity and performance.
read the caption
Table 1: Summary of instance-dependent results in offline RL with linear function approximation.
In-depth insights#
Robust Offline RL#
Robust offline reinforcement learning (RL) addresses the limitations of standard offline RL by explicitly considering model uncertainty. Unlike standard offline RL which assumes the training data perfectly represents the deployment environment, robust offline RL acknowledges that this assumption might be violated due to shifts in environmental dynamics. This is crucial in real-world applications where perfect data matching is unlikely. The core challenge in robust offline RL lies in efficiently training policies that remain effective across a range of plausible environmental variations. Techniques often involve modeling dynamics uncertainty using methods like distributionally robust Markov decision processes (DRMDPs), which aim to optimize the worst-case performance. Function approximation is key to handling large state-action spaces, introducing computational complexity and necessitating clever algorithmic approaches like those based on pessimism principles and variance information incorporation. Analyzing suboptimality is important to guarantee performance bounds. The study of instance-dependent suboptimality and the development of computationally efficient algorithms are active areas of research in robust offline RL. Theoretical guarantees are vital to ensure that robust methods achieve meaningful improvements.
Function Approx#
Function approximation is crucial for scaling reinforcement learning (RL) algorithms to handle large state and action spaces. In the context of distributionally robust offline RL, function approximation presents unique challenges due to the introduction of nonlinearity from dynamics uncertainty. Existing methods often struggle with computational efficiency and/or provide weak theoretical guarantees. This paper tackles these challenges by focusing on a linearly-parameterized setting, resulting in computationally efficient algorithms while still enabling theoretical analysis. A novel function approximation mechanism is introduced, leveraging variance information to enhance performance and leading to improved theoretical upper bounds. This is a significant contribution, as it demonstrates that minimax optimality and computational tractability can be achieved even when dealing with model uncertainty in offline RL settings, paving the way for applying robust RL techniques to more complex real-world problems.
DRPVI Algorithm#
The DRPVI (Distributionally Robust Pessimistic Value Iteration) algorithm is a computationally efficient method for solving distributionally robust Markov decision processes (DR-MDPs) with linear function approximation. Its core innovation lies in incorporating a novel function approximation mechanism that explicitly accounts for the model uncertainty inherent in DR-MDPs. This is achieved by introducing a robust penalty term that effectively penalizes the optimistic estimation error caused by the uncertainty set. DRPVI cleverly employs a pessimistic principle, which guarantees the algorithm’s minimax optimality in achieving the optimal robust policy. This optimality is further enhanced by its instance-dependent suboptimality analysis, providing insights into the algorithm’s performance based on specific problem instances and data characteristics. Furthermore, the algorithm’s computational efficiency is a significant advantage given the inherent challenges of DR-MDPs in handling large state-action spaces. This efficiency stems from its use of a diagonal-based normalization rather than the computationally expensive Mahalanobis norm found in similar algorithms.
VA-DRPVI Enhance#
The enhancement of VA-DRPVI, a variance-aware algorithm for distributionally robust offline reinforcement learning, focuses on improving its computational efficiency and theoretical guarantees. A key aspect is the incorporation of variance information, leading to a tighter upper bound on the suboptimality gap. This is achieved by leveraging a range shrinkage property inherent in the robust value function, showing that under model uncertainty, the range of possible value function values is smaller than in standard MDPs. The algorithm also utilizes a novel function approximation mechanism that incorporates variance information, resulting in a more statistically efficient estimation process. The combination of improved theoretical guarantees and enhanced computational efficiency marks a significant advancement in the field, enabling its application to larger-scale problems where standard robust offline RL methods struggle.
Lower Bound#
The lower bound analysis is crucial for understanding the fundamental limits of distributionally robust offline reinforcement learning (RL). This section rigorously proves that a specific uncertainty function, deeply connected to the covariance matrix and feature mapping, forms an unavoidable barrier in achieving optimal performance. This lower bound is shown to match the upper bound of the proposed VA-DRPVI algorithm up to a constant factor, establishing near-optimality and demonstrating the algorithm’s efficiency. The construction of hard instances and the mathematical proof techniques used to establish this lower bound represent a significant contribution to the theory of robust offline RL, offering valuable insights into the inherent challenges of balancing robustness against computational complexity. The results highlight the differences between standard offline RL and the distributionally robust setting. The instance-dependent nature of both upper and lower bounds underscores the difficulty of providing uniform guarantees and the importance of carefully analyzing specific problem instances. In short, this theoretical analysis is vital in shaping future research in robust offline RL by providing a benchmark for evaluating algorithms and demonstrating the inherent limitations of function approximation in this complex setting.
More visual insights#
More on figures
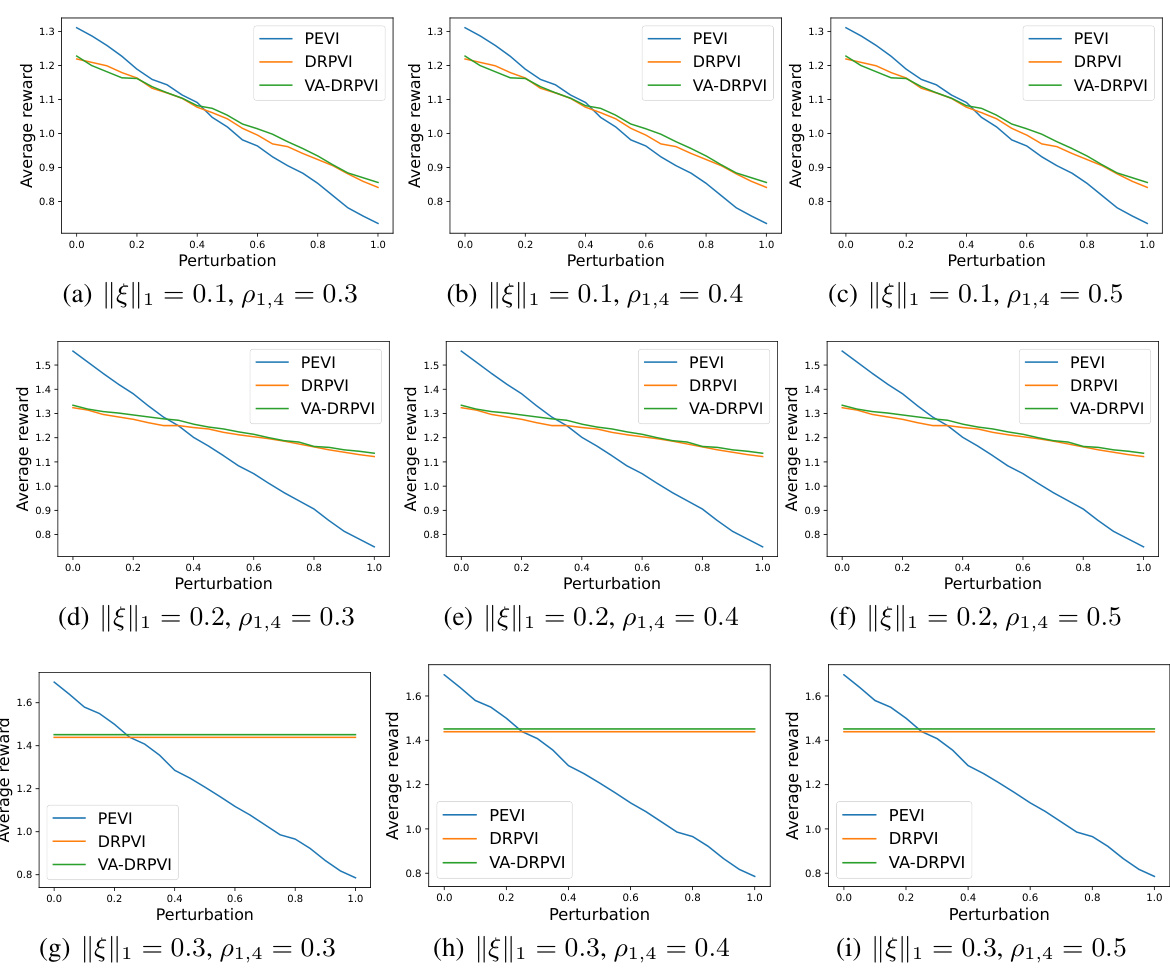
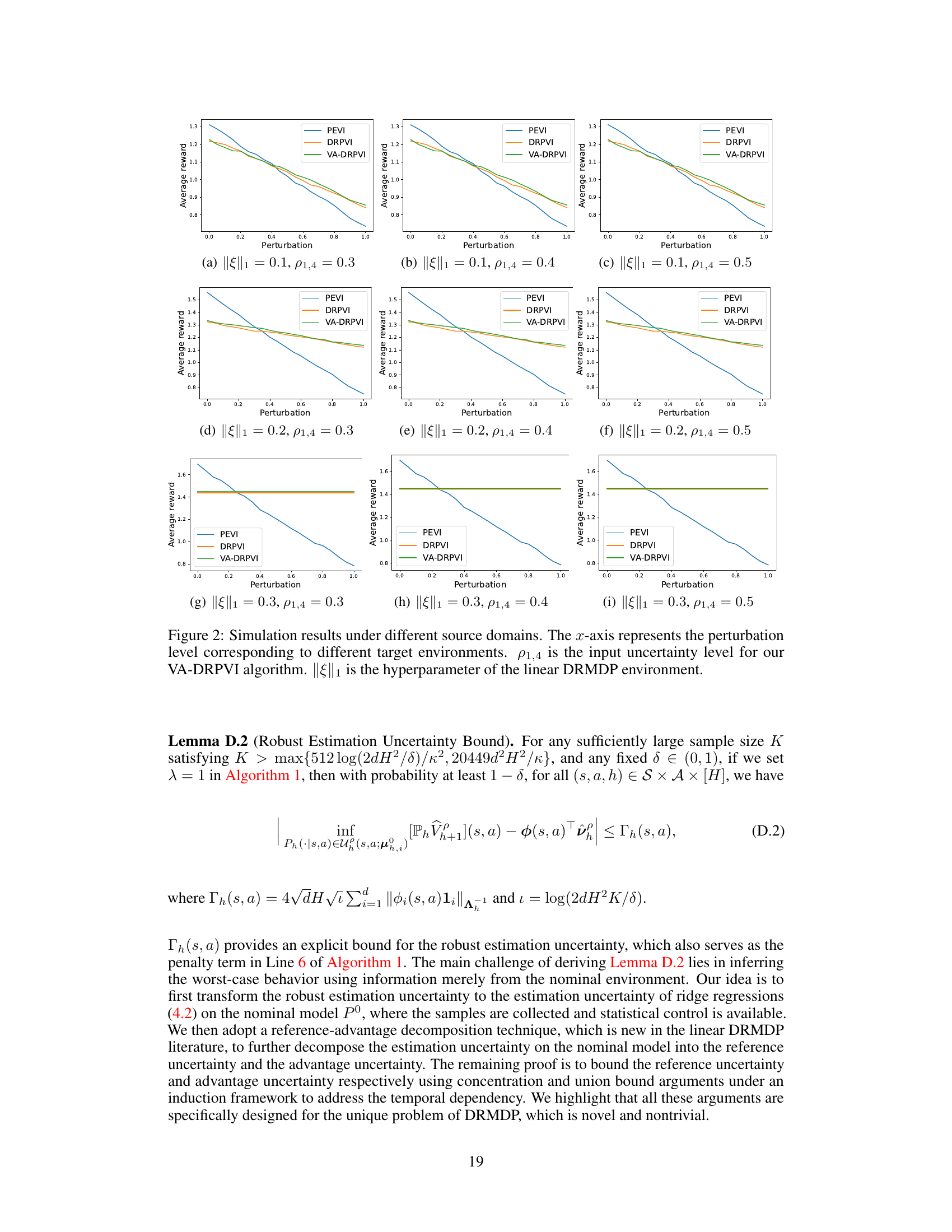
🔼 This figure shows the experimental results of three algorithms (PEVI, DRPVI, VA-DRPVI) under different settings. The x-axis represents the perturbation level, which corresponds to the difference between the source and target environment. The y-axis represents the average reward achieved by the learned policy of each algorithm under different levels of perturbation. The three sub-figures represent different values of ||ξ||1 (a hyperparameter) while each sub-figure includes three plots that correspond to different values of ρ1,4 (uncertainty level).
read the caption
Figure 2: Simulation results under different source domains. The x-axis represents the perturbation level corresponding to different target environments. ρ1,4 is the input uncertainty level for our VA-DRPVI algorithm. ||ξ||1 is the hyperparameter of the linear DRMDP environment.
🔼 This figure shows the source and target Markov Decision Processes used in the paper’s experiments. The source MDP is a small MDP with five states and three steps, while the target MDP is designed by introducing perturbation at the transition probability at the first step of the source MDP. The purpose is to demonstrate the impact of distribution shifts on robust offline RL. The figure depicts the transition probabilities of both environments, visually illustrating how the target environment deviates from the source environment.
read the caption
Figure 1: The source and the target linear MDP environments. The value on each arrow represents the transition probability. For the source MDP, there are five states and three steps, with the initial state being x1, the fail state being x4, and x5 being an absorbing state with reward 1. The target MDP on the right is obtained by perturbing the transition probability at the first step of the source MDP, with others remaining the same.
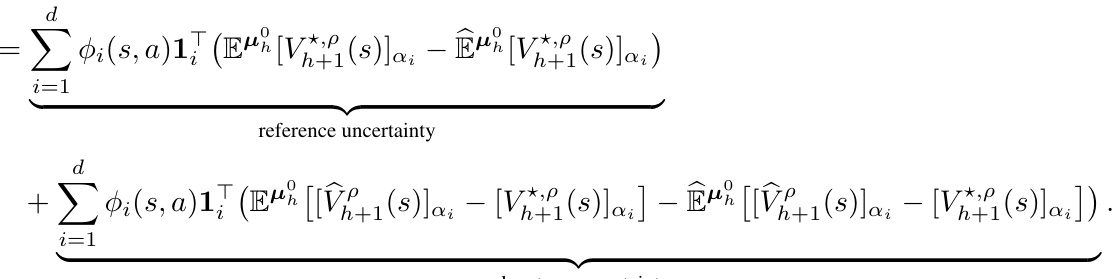
🔼 The figure shows the performance comparison of three algorithms (PEVI, DRPVI, and VA-DRPVI) under different perturbation levels and hyperparameter settings. The x-axis represents the level of perturbation introduced in the target environment (relative to the source environment). The y-axis shows the average reward achieved by each algorithm. The different subplots represent different choices of hyperparameters, illustrating the impact of uncertainty level and feature mapping on the algorithms’ robustness. Generally, VA-DRPVI and DRPVI are shown to be more robust than PEVI to the environmental perturbations.
read the caption
Figure 2: Simulation results under different source domains. The x-axis represents the perturbation level corresponding to different target environments. ρ1,4 is the input uncertainty level for our VA-DRPVI algorithm. ||Φ||1 is the hyperparameter of the linear DRMDP environment.
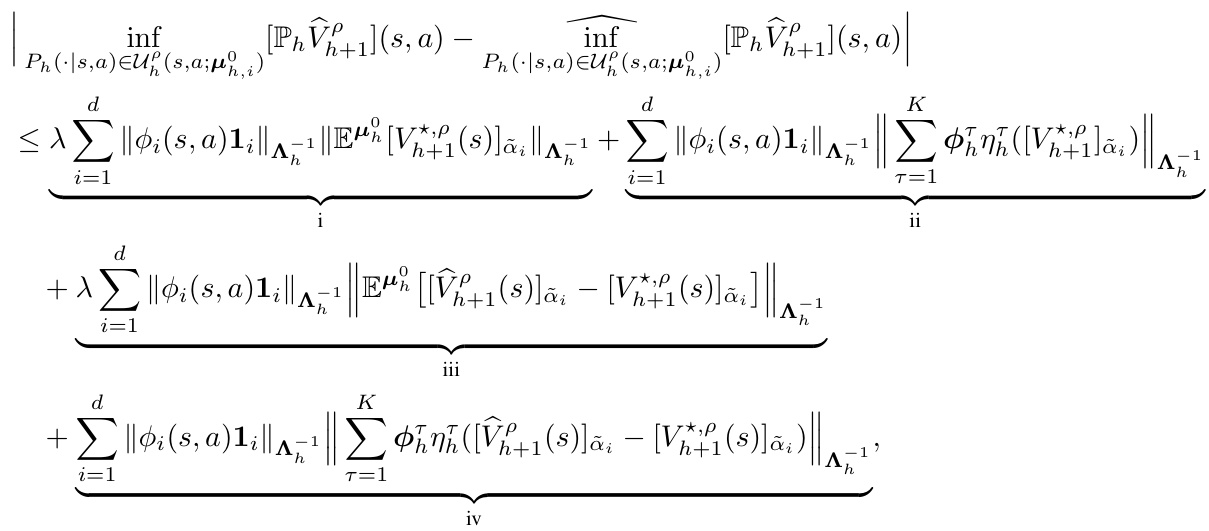
🔼 The figure shows the performance of three algorithms (DRPVI, VA-DRPVI, and PEVI) under different environmental perturbation levels and hyperparameter settings. The x-axis represents the level of perturbation introduced into the target environment (compared to the source). The y-axis is the average performance (cumulative reward). Different subfigures represent different hyperparameter settings, showing the algorithms’ robustness across various conditions. VA-DRPVI generally outperforms DRPVI and PEVI.
read the caption
Figure 2: Simulation results under different source domains. The x-axis represents the perturbation level corresponding to different target environments. ρ1,4 is the input uncertainty level for our VA-DRPVI algorithm. ||ξ||1 is the hyperparameter of the linear DRMDP environment.
Full paper#