TL;DR#
Training massive Transformer models has been incredibly successful, yet a theoretical understanding of why these models converge globally during training has been lacking. This paper tackles this challenge by rigorously analyzing the convergence properties of gradient flow in training Transformers with weight decay regularization. The researchers identified a critical issue: existing convergence analysis tools for deep neural networks rely on strong assumptions (homogeneity and global Lipschitz smoothness), which are not applicable to Transformers.
The researchers overcame this obstacle by developing novel mean-field techniques tailored specifically for Transformers. They successfully proved that gradient flow in large-scale Transformer models converges to a global minimum consistent with the solution to a partial differential equation (PDE) under sufficiently small weight decay regularization. Their results offer significant insights into why Transformers consistently find global solutions despite the highly non-convex landscape of the training objective, paving the way for more efficient and stable training methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with large-scale Transformer models. It provides the first rigorous global convergence guarantees for Transformer training, addressing a major gap in our understanding of their optimization. This opens new avenues for improving training efficiency and stability, and provides valuable theoretical insights into the behavior of these complex models. The novel mean-field techniques introduced are also of independent interest to the broader deep learning community.
Visual Insights#
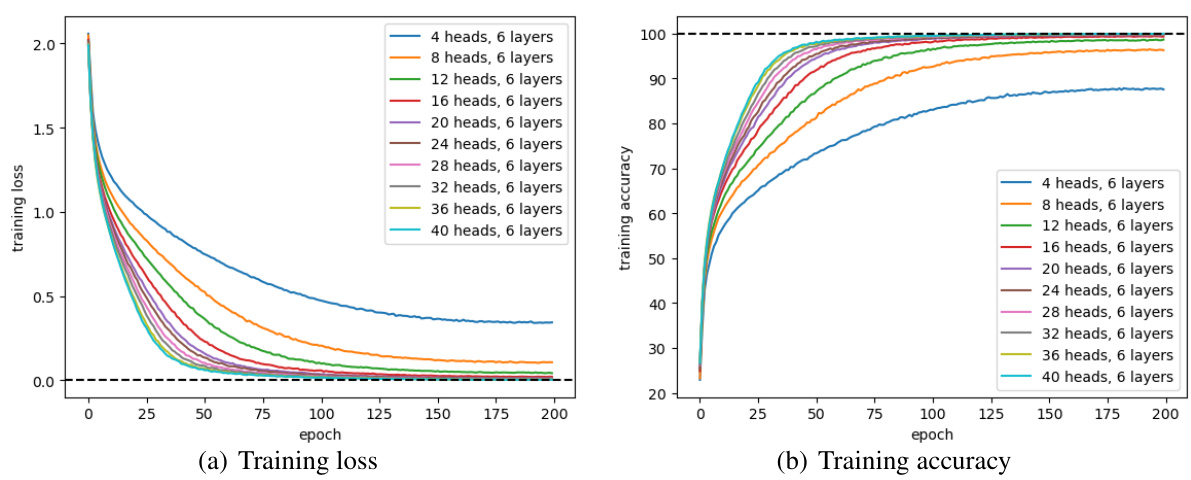
🔼 This figure shows the training loss and training accuracy curves for Vision Transformers with varying numbers of heads, while keeping the number of layers constant at 6. The x-axis represents the training epoch, and the y-axis shows either training loss (left panel) or training accuracy (right panel). Multiple curves are shown, each representing a different number of heads (ranging from 4 to 40). The figure demonstrates the relationship between the model’s width (number of heads) and its training performance. As the number of heads increases, the model typically achieves lower training loss and higher training accuracy.
read the caption
Figure 1: Training loss and training accuracy of Vision Transformers with different numbers of heads. (a) gives the curves of training loss, while (b) gives the curves of training accuracy.
Full paper#



















