Coded Computing for Resilient Distributed Computing: A Learning-Theoretic Framework

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in distributed computing and machine learning. It provides a novel learning-theoretic framework for coded computing, overcoming limitations of existing algebraic approaches. This opens avenues for designing efficient and resilient distributed ML systems, improving accuracy and convergence rates. The framework’s applicability to various machine learning models and its superior performance compared to state-of-the-art methods make it highly relevant to current research trends.

Visual Insights

#

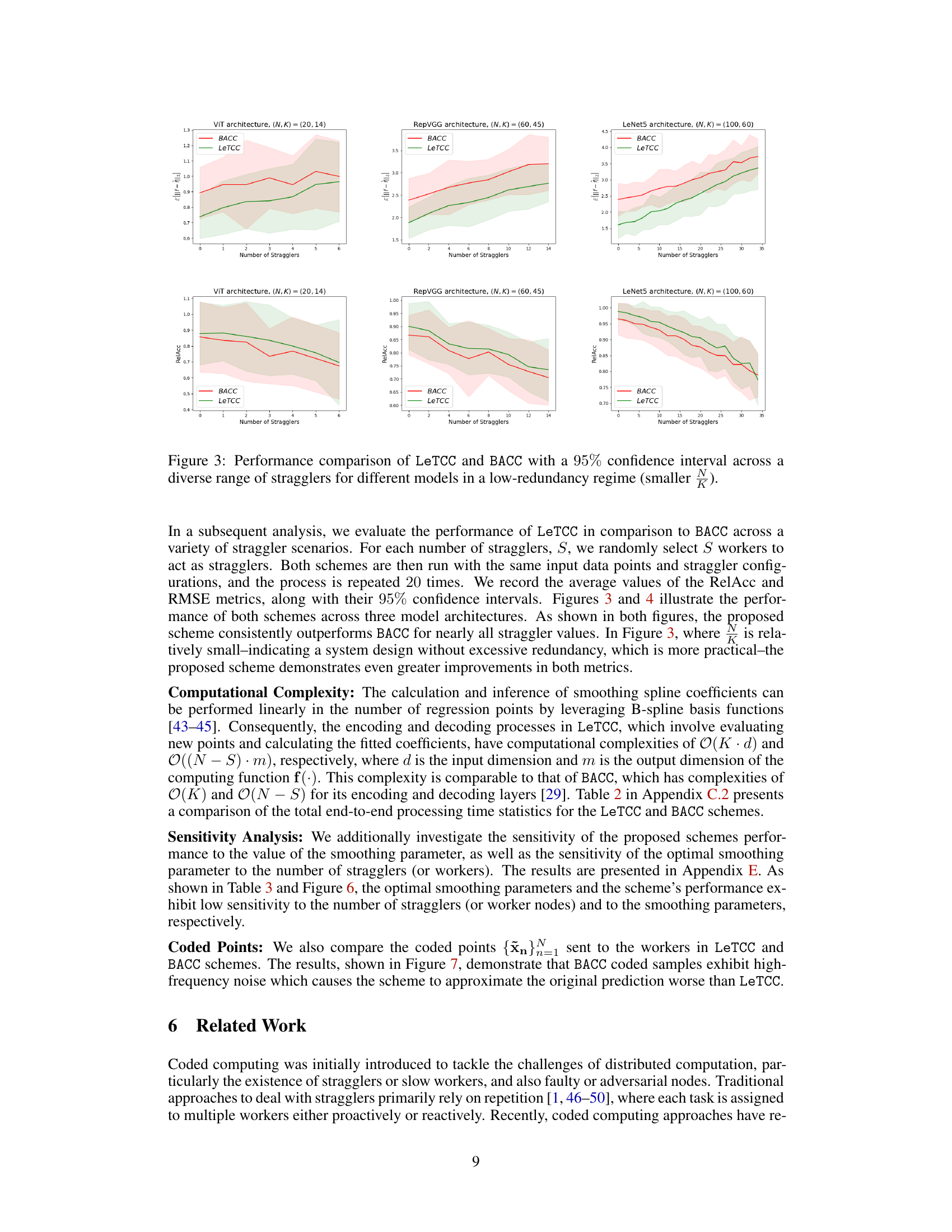
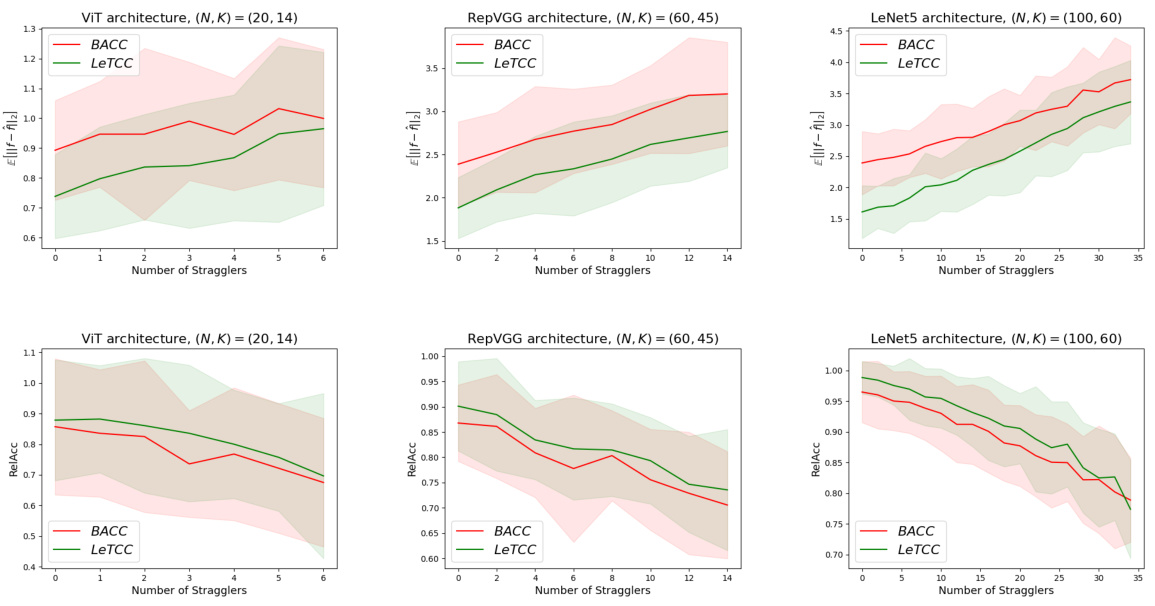
🔼 Figure 1(a) shows the coded computing process. The encoder sends coded data to each worker. The worker processes the data and sends the results back to the master node. The decoder recovers the final results from the computation results from the workers, even if some worker nodes fail (stragglers). Figure 1(b) compares the performance of the proposed learning-theoretic coded computing (LeTCC) framework with the state-of-the-art BACC framework. The plot shows that LeTCC achieves lower estimation error and faster convergence rate.

read the caption

Figure 1(a): Coded Computing: Each worker node processes a combination of data (coded data). The decoder recovers the final results, even in the presence of missing outputs from some worker nodes. Figure 1(b): The log-log plot of the expected error versus the number of workers (N) for the proposed framework (LeTCC) and the state-of-the-art BACC [29]. LeTCC framework not only achieves a lower estimation error but also has a faster convergence rate.

🔼 The table compares the performance of the proposed LeTCC framework and the state-of-the-art BACC framework in terms of RMSE and relative accuracy (RelAcc). The comparison is done across three different neural network architectures (LeNet5, RepVGG, and ViT) with varying numbers of workers (N), data points (K), and non-straggler worker nodes (|F|). Lower RMSE and higher RelAcc values indicate better performance.

read the caption

Table 1: Comparison of the proposed framework (LeTCC) and the state-of-the-art (BACC) in terms of the Root Mean Squared Error (RMSE) and the Relative Accuracy (RelAcc).

In-depth insights

#

Coded Computing Intro

#

Coded computing is presented as a solution to the challenges of large-scale distributed computing, particularly concerning slow or unreliable worker nodes (stragglers) and the potential for data compromise. The introduction highlights the significant impact of stragglers on overall computation efficiency and the need for robust mechanisms to maintain data accuracy and integrity in the presence of faulty or malicious workers. It establishes the importance of coded computing by leveraging coding theory to introduce redundancy and resilience into the system. Existing approaches, often rooted in algebraic coding theory and drawing parallels to communication systems, are discussed as limited in their adaptability to various computation functions and machine learning workloads, often requiring restrictive assumptions. The introduction sets the stage for a proposed new framework that aims to overcome these limitations by grounding the approach in learning theory, adapting seamlessly to diverse machine learning applications.

Learning-Theoretic Core

#

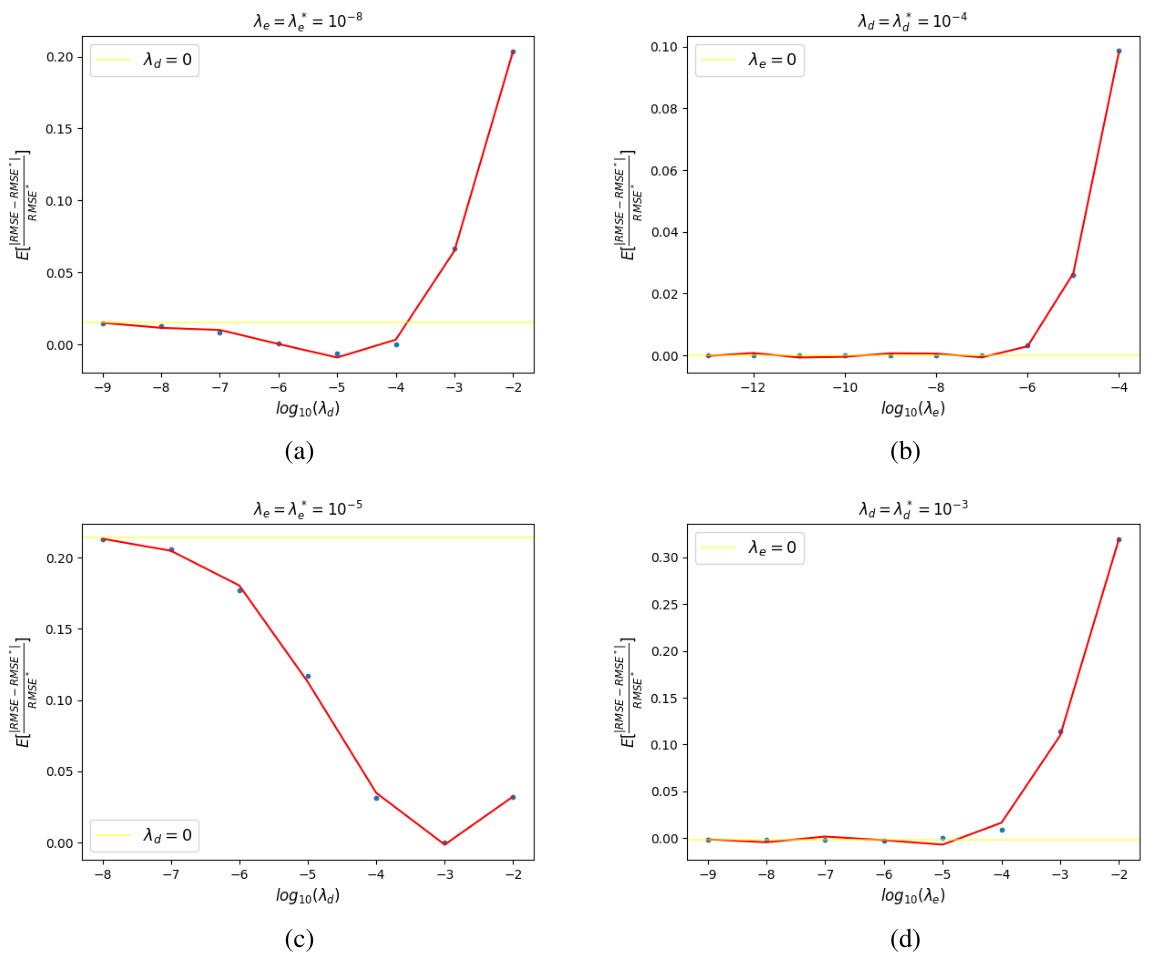
A learning-theoretic framework for coded computing is presented, offering a novel approach to enhance the reliability and efficiency of large-scale distributed computing systems. The core of this framework lies in its integration of learning theory, moving beyond traditional coding-centric methods. By defining the loss function as the mean squared error, the approach seeks to optimize both the encoder and decoder functions to minimize this error. Upper bounds on the loss function are derived, separating the generalization error of the decoder and the training error of the encoder. This decomposition facilitates the derivation of optimal encoder and decoder functions within specific function spaces (e.g., second-order Sobolev spaces). The framework’s effectiveness is demonstrated through theoretical analysis of convergence rates and empirical evaluations showing improved accuracy and convergence speed over state-of-the-art methods. The key innovation is framing the problem as an optimization task within a learning framework, leveraging established tools from learning theory for improved performance and generalizability.

LeTCC Framework

#

The LeTCC framework presents a novel approach to coded computing, integrating learning theory principles to enhance its adaptability and effectiveness in distributed computing settings, particularly for machine learning tasks. Unlike traditional coded computing methods that rely heavily on algebraic coding theory, LeTCC focuses on optimizing encoding and decoding functions to minimize the mean squared error. This is achieved by bounding the loss function, which allows for a more efficient search for optimal functions. The framework’s strength lies in its ability to seamlessly integrate with machine learning applications, enabling optimal solutions for diverse computation functions in the presence of stragglers or noisy computations. Its theoretical foundation is robust, providing convergence rate analysis. Importantly, LeTCC demonstrates superior performance in both accuracy and convergence rate compared to existing methods across a range of experiments. The framework also shows resilience to noise and stragglers in various computation scenarios, making it a promising solution for resilient distributed computing applications.

Empirical Validation

#

An empirical validation section would rigorously test the proposed learning-theoretic coded computing framework’s performance. It would involve evaluating the framework’s accuracy and convergence rate on diverse machine learning models and datasets. Key metrics such as root mean squared error (RMSE) and relative accuracy (RelAcc) would be meticulously analyzed. Different noise levels and straggler scenarios need to be simulated to showcase the framework’s robustness. Comparisons with state-of-the-art techniques are essential, providing a quantitative assessment of improvements in accuracy and convergence speed. The experimental setup should be precisely described, ensuring reproducibility. Finally, a discussion of the results is crucial, highlighting both strengths and limitations observed during the validation process. Addressing potential limitations and proposing future research directions would further enhance this section.

Future Work

#

The paper’s “Future Work” section could explore several promising avenues. Extending the framework to handle Byzantine failures is crucial for real-world deployment, where malicious or faulty nodes could compromise results. A natural next step is integrating differential privacy to ensure the privacy of sensitive data during distributed computation. The theoretical analysis could be extended beyond second-order Sobolev spaces to accommodate a broader range of functions, potentially improving performance and applicability. Moreover, investigating the optimal selection of interpolation points and their influence on accuracy and convergence is a significant area for improvement. Finally, comprehensive empirical validation on larger-scale datasets with diverse machine learning models and more complex computations would further solidify the framework’s effectiveness and reveal its potential limitations in different deployment scenarios. This would particularly benefit understanding the trade-offs between accuracy and computational efficiency.

More visual insights

#

More on figures

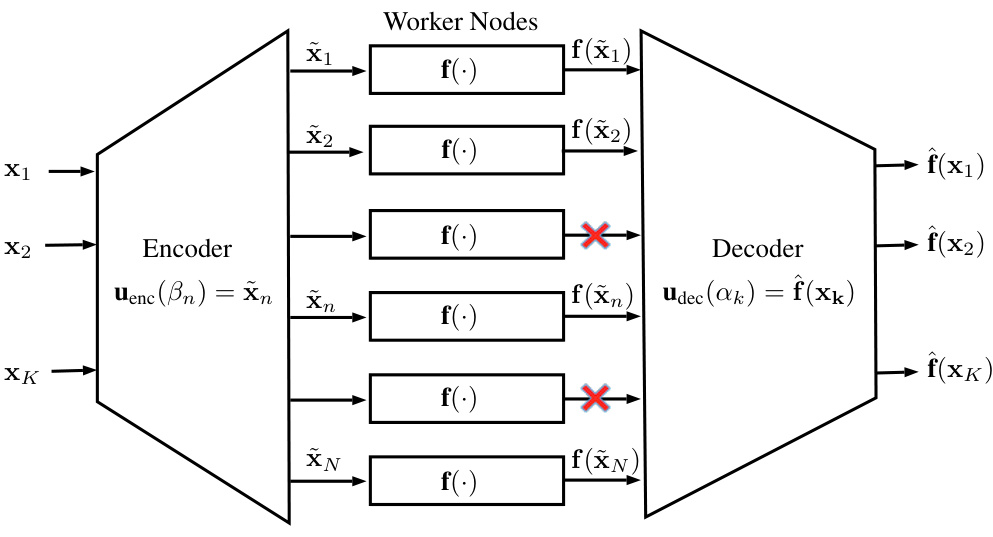
🔼 The figure illustrates the LeTCC (Learning-Theoretic Coded Computing) framework, showing its three layers: the encoding layer, the computing layer, and the decoding layer. The encoding layer takes raw data points (x1, x2,…xK) as input and produces coded data points (x1, x2,…xN) which are then sent to the worker nodes. Each worker node applies a function, f(.), to its assigned coded data point and returns the result. In the computing layer, some worker nodes might be stragglers and fail to return results. Finally, the decoding layer takes the results from the non-straggler worker nodes and reconstructs the desired results (f(x1), f~(x2),…f~(xK)). The framework is designed for straggler resilience.

read the caption

Figure 2: LeTCC framework.

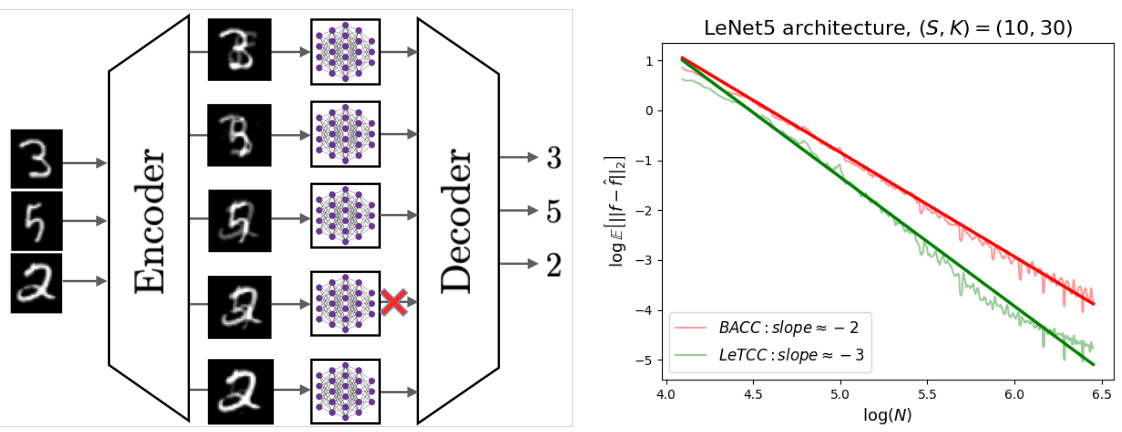
🔼 This figure shows the log-log plot of the expected error against the number of workers for both the proposed LeTCC framework and the state-of-the-art BACC framework. The plot clearly demonstrates that LeTCC achieves a significantly lower estimation error and a faster convergence rate compared to BACC.

read the caption

Figure 1(b): The log-log plot of the expected error versus the number of workers (N) for the proposed framework (LeTCC) and the state-of-the-art BACC [29]. LeTCC framework not only achieves a lower estimation error but also has a faster convergence rate.

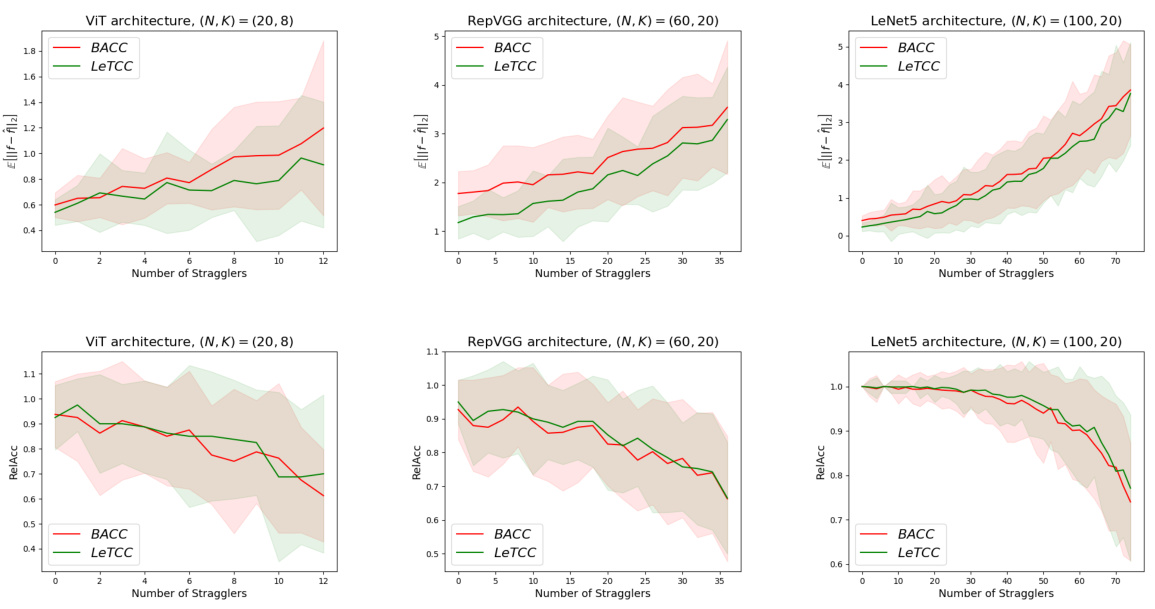
🔼 This figure compares the performance of the proposed LeTCC framework and the state-of-the-art BACC framework in terms of the expected error versus the number of workers. The log-log plot shows that LeTCC achieves a lower estimation error and a faster convergence rate than BACC.

read the caption

Figure 1(b): The log-log plot of the expected error versus the number of workers (N) for the proposed framework (LeTCC) and the state-of-the-art BACC [29]. LeTCC framework not only achieves a lower estimation error but also has a faster convergence rate.

🔼 Figure 1(a) shows a schematic of coded computing, where each worker node receives a coded combination of the input data and performs computation on it. The decoder at the master node then uses the outputs from the worker nodes to recover the final results even if some worker nodes are slow or missing. Figure 1(b) compares the performance of the proposed LeTCC framework with the state-of-the-art BACC framework in terms of the expected error versus the number of worker nodes. The plot shows that LeTCC achieves both a lower expected error and a faster convergence rate.

read the caption

Figure 1(a): Coded Computing: Each worker node processes a combination of data (coded data). The decoder recovers the final results, even in the presence of missing outputs from some worker nodes. Figure 1(b): The log-log plot of the expected error versus the number of workers (N) for the proposed framework (LeTCC) and the state-of-the-art BACC [29]. LeTCC framework not only achieves a lower estimation error but also has a faster convergence rate.

🔼 This figure shows the comparison of the proposed LeTCC framework and the state-of-the-art BACC framework in terms of the expected error with respect to the number of workers. It demonstrates that LeTCC outperforms BACC in terms of both accuracy and convergence speed.

read the caption

Figure 1(b): The log-log plot of the expected error versus the number of workers (N) for the proposed framework (LeTCC) and the state-of-the-art BACC [29]. LeTCC framework not only achieves a lower estimation error but also has a faster convergence rate.

🔼 This figure illustrates the basic concept of coded computing. Data is encoded at a master node and distributed to multiple worker nodes for parallel processing. Each worker receives a combination of the original data, rather than the raw data itself. The final results are then reconstructed by a decoder at the master node, even if some worker nodes are slow or fail to respond (stragglers). This approach increases resilience to stragglers compared to traditional distributed computing methods.

read the caption

Figure 1(a): Coded Computing: Each worker node processes a combination of data (coded data). The decoder recovers the final results, even in the presence of missing outputs from some worker nodes.

🔼 This figure illustrates the basic concept of coded computing. The master node encodes the data and distributes it to multiple worker nodes. Each worker node processes its assigned encoded data and returns the results to the master node. The decoder then uses the results from all the worker nodes (or a subset of them, as some may be slow or faulty) to reconstruct the final output. The redundancy in the encoded data allows the decoder to compensate for missing or incorrect results. This is a key part of the paper’s methodology, allowing resilient computing.

read the caption

Figure 1(a): Coded Computing: Each worker node processes a combination of data (coded data). The decoder recovers the final results, even in the presence of missing outputs from some worker nodes.

🔼 This figure illustrates the basic concept of coded computing. Data is encoded by a master node and distributed to worker nodes for processing. Each worker node receives a coded combination of data, not the raw data itself. Worker nodes perform their assigned computation and return their results to the master node. The master node employs a decoder to reconstruct the final result from the collective outputs of the worker nodes, even if some workers (stragglers) fail to respond or produce correct results. This approach leverages the redundancy in the coded data to enhance reliability and resilience against stragglers.

read the caption

Figure 1(a): Coded Computing: Each worker node processes a combination of data (coded data). The decoder recovers the final results, even in the presence of missing outputs from some worker nodes.

More on tables

🔼 This table compares the performance of the proposed LeTCC framework and the state-of-the-art BACC framework in terms of RMSE and relative accuracy (RelAcc) across three different model architectures: LeNet5, RepVGG, and ViT. For each model, the table shows the RMSE and RelAcc values for both LeTCC and BACC, along with their standard deviations, for a specific configuration of the number of workers (N), data points (K), and non-straggler workers (|F|).

read the caption

Table 1: Comparison of the proposed framework (LeTCC) and the state-of-the-art (BACC) in terms of the Root Mean Squared Error (RMSE) and the Relative Accuracy (RelAcc).

🔼 This table compares the performance of the proposed LeTCC framework and the state-of-the-art BACC method in terms of RMSE and relative accuracy (RelAcc). The comparison is done across three different neural network architectures: LeNet5, RepVGG, and ViT. For each architecture, the table shows the RMSE and RelAcc values for both methods, with different numbers of worker nodes (N), data points (K), and non-straggler worker nodes (|F|). This allows for an assessment of the relative performance of the two methods under various conditions.

read the caption

Table 1: Comparison of the proposed framework (LeTCC) and the state-of-the-art (BACC) in terms of the Root Mean Squared Error (RMSE) and the Relative Accuracy (RelAcc).

Full paper

#