TL;DR#
Traditional one-size-fits-all models often fail to capture individual variations in complex data like brain imaging. This paper tackles this challenge by proposing a novel individualized modeling approach called Attention boosted Individualized Regression (AIR). Existing methods often require additional information on sample similarity, making them unsuitable for many real-world applications. AIR addresses this issue by focusing on heterogeneity within samples.
AIR achieves individualization by learning an optimal internal relation map within each sample. This internal relation map allows the model to capture local dependencies between different parts of the input data, improving both predictive accuracy and model interpretability. The method’s effectiveness is demonstrated through numerical experiments and a real-world brain MRI analysis, showcasing superior performance compared to other state-of-the-art methods. The close connection between AIR and the self-attention mechanism also provides a valuable new perspective on attention.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel individualized modeling framework for matrix-valued data, addressing the limitations of existing methods that rely on sample similarity. It offers a new interpretation of the self-attention mechanism and demonstrates superior performance in brain MRI analysis. This work opens new avenues for personalized medicine and brain connectomics research by enabling the use of sample-specific internal relations to enhance model interpretability and prediction accuracy.
Visual Insights#
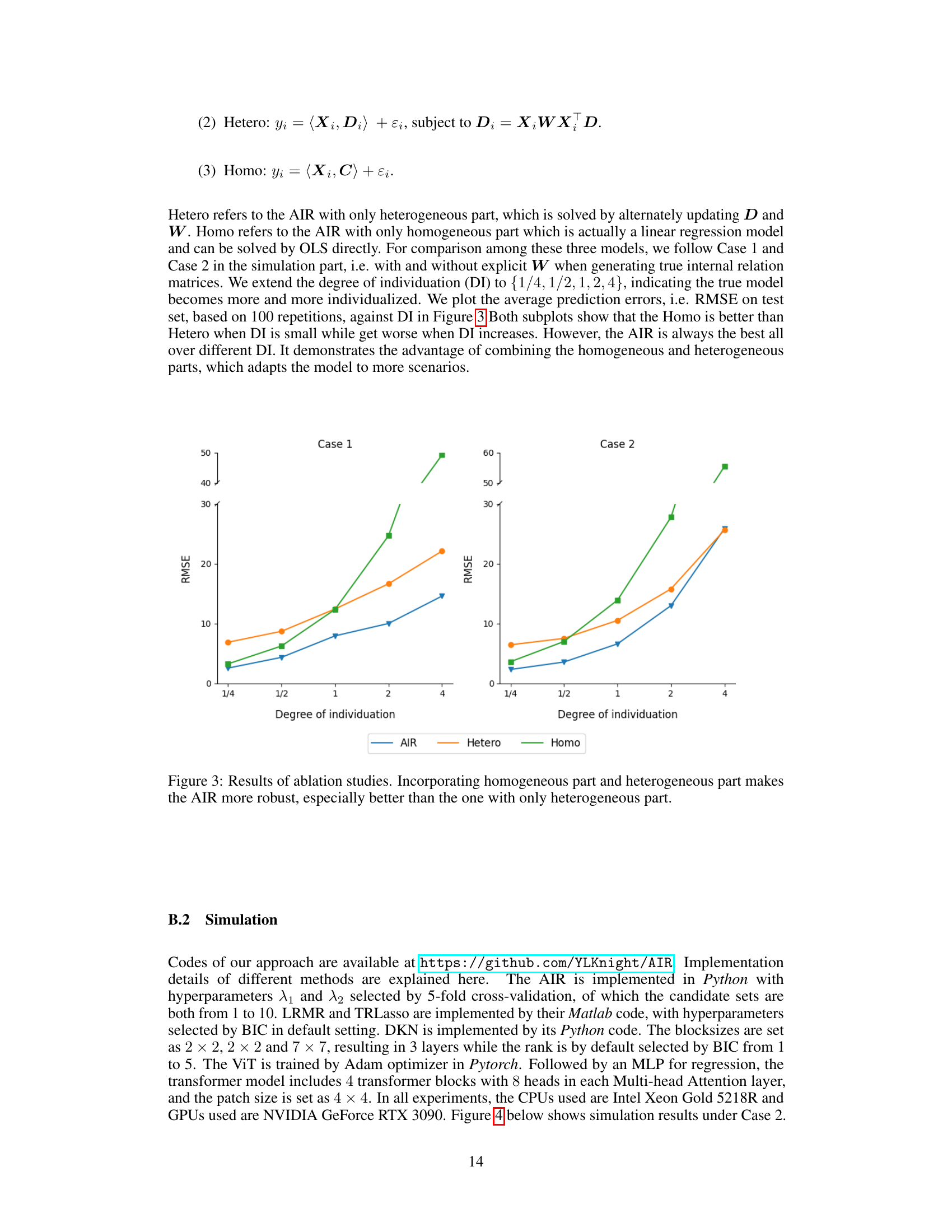
🔼 This figure displays the results of a simulation study with a degree of individuation (DI) of 1.0, comparing the performance of the proposed Attention boosted Individualized Regression (AIR) model with other existing methods (LRMR, TRLasso, DKN, OLS). The first three columns show the true parameter values and the estimations produced by AIR, demonstrating the model’s ability to accurately recover the true values. The subsequent columns show estimations obtained using other regression techniques. By comparing the results, one can assess the relative performance and accuracy of the different methods in recovering the true parameter values.
read the caption
Figure 1. Case 1 simulation results with DI = 1.0. The first three columns show true parameters and estimations from AIR. The last two columns show estimations from other methods except ViT, as it has no explicit coefficient matrix. An additional OLS estimation is added for reference.
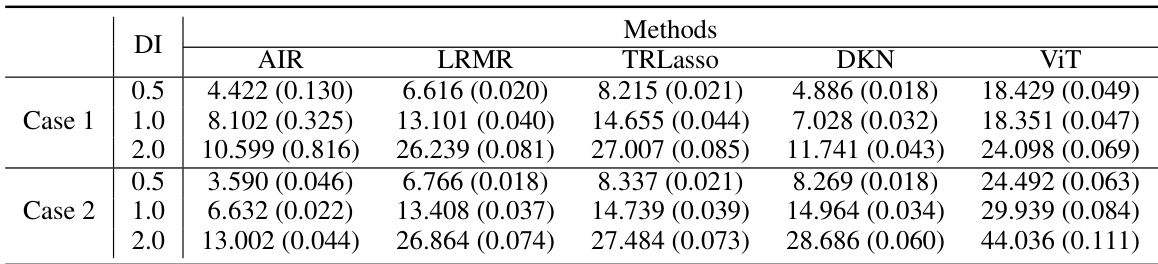
🔼 This table presents the prediction error (RMSE) results on a test set for various methods, including AIR, LRMR, TRLasso, DKN, and ViT, across different levels of model individualization (DI) and experimental conditions (Case 1 and Case 2). The numbers represent the average RMSE and its standard error over 100 repetitions. Case 1 and Case 2 represent different correlation structures between image blocks in the input data. Lower RMSE values indicate better performance.
read the caption
Table 1: Prediction errors of different methods.
In-depth insights#
Attention-Boosted Regression#
The concept of ‘Attention-Boosted Regression’ blends the power of attention mechanisms, commonly used in deep learning, with the statistical elegance of regression models. The core idea is to leverage the ability of attention to weigh different parts of the input data differently, thus creating a more individualized and nuanced regression model. This approach moves beyond the traditional one-size-fits-all regression, which assumes a single set of parameters for all data points. Instead, attention-boosted regression could dynamically adapt to the specific characteristics of each data point, yielding more accurate and personalized predictions. This could involve learning sample-specific attention weights that highlight relevant features or employing a learned attention mechanism to determine the optimal weighting of different input features for each regression task. The key benefit lies in the improved adaptability and robustness of the model, allowing it to handle complex data relationships that might be missed by standard regression methods. However, designing and training such a model effectively requires careful consideration of the attention mechanism’s computational complexity and potential overfitting issues. Careful regularization and efficient implementations are crucial to realize the full potential of this innovative approach.
Individualized Modeling#
Individualized modeling contrasts with the traditional one-size-fits-all approach by tailoring models to individual characteristics. This paradigm shift is particularly crucial in domains like medicine and finance where heterogeneity among individuals significantly impacts outcomes. The core idea revolves around adapting model parameters to specific subjects, leading to better predictions, personalized insights, and potentially more effective interventions. However, individualized modeling presents several challenges. Acquiring sufficient data for each individual can be difficult, potentially leading to overfitting. Furthermore, developing effective methods for handling the high dimensionality and variability across individuals requires careful consideration. The choice of individualization strategy, whether through varying coefficients, hierarchical models, or other approaches, significantly impacts model performance and interpretability. Balancing the benefits of personalization against the risks of overfitting and computational complexity is a key consideration in developing successful individualized models. Successfully addressing these challenges offers the potential for substantial progress in diverse fields.
Internal Relation Maps#
The concept of “Internal Relation Maps” in the context of a research paper likely revolves around representing and utilizing the relationships between different components or features within a single data instance. Instead of focusing solely on inter-sample relationships, internal relation maps emphasize the intra-sample structure. This is particularly relevant for complex data like images or brain networks where local dependencies and correlations within the data are crucial. The maps could be constructed using various techniques, such as correlation matrices, similarity measures, or learned representations from neural networks. The power of this approach lies in its ability to capture nuanced patterns not apparent in simpler representations. By incorporating internal relations into models, particularly in individualized settings, the analysis gains significant granularity and potential improvements in prediction accuracy and interpretation. The choice of method for generating these maps would depend heavily on the specific data type and application, with considerations including computational efficiency and the interpretability of the resulting representation. Effective use of internal relation maps likely improves model performance in applications like personalized medicine and connectomics.
Matrix-Valued Data#
Matrix-valued data, representing information as matrices rather than vectors, presents unique challenges and opportunities in data analysis. The inherent structure of matrices, capturing relationships between variables in a multi-dimensional way, allows for modeling complex interactions and dependencies often missed by simpler vector-based approaches. Analyzing this data effectively requires methods that can handle the high dimensionality and potential for missing values or noise. Individualized regression techniques, for example, offer an elegant solution by allowing model parameters to vary across samples, adapting to unique characteristics of each matrix. The ability to capture local dependencies within each matrix through sample-specific internal relation maps, as explored in the concept of attention mechanisms, is crucial. This not only enhances predictive accuracy but also improves interpretability by revealing underlying relationships between the data points within each matrix. Effective analysis often leverages techniques that capture both common patterns across all matrices and unique characteristics of each individual matrix, resulting in hybrid models that balance generalization with personalization. Overall, research into matrix-valued data is important for unlocking insights from complex, real-world phenomena, particularly in fields like personalized medicine and brain connectomics where rich relational data abounds.
ADNI Dataset Analysis#
In the ADNI dataset analysis section, the researchers would likely present the results of applying their Attention boosted Individualized Regression (AIR) model to predict cognitive decline using brain MRI data. Key aspects of this analysis would include: the model’s performance metrics (RMSE, etc.) compared to existing methods; visualizations showcasing how well AIR captures individual variations in brain connectivity and their relation to cognitive scores; an examination of whether the identified heterogeneity aligns with clinical understanding of AD progression. The success of the AIR model in this context would validate its ability to capture nuanced individual variations and demonstrate its potential for personalized medicine and brain connectomics research. Important considerations would be whether the model generalizes well across diverse ADNI subgroups and the reliability of using MRI data alone to make predictions. A thoughtful discussion of the results would emphasize the implications of individual-level modeling, its potential limitations, and future research directions. The limitations section will explore whether additional variables (demographic, genetic, clinical information) could improve the accuracy and generalizability of the model, the potential influence of noise or artifacts in the MRI scans, and the need for larger, more diverse datasets to further validate the results.
More visual insights#
More on figures
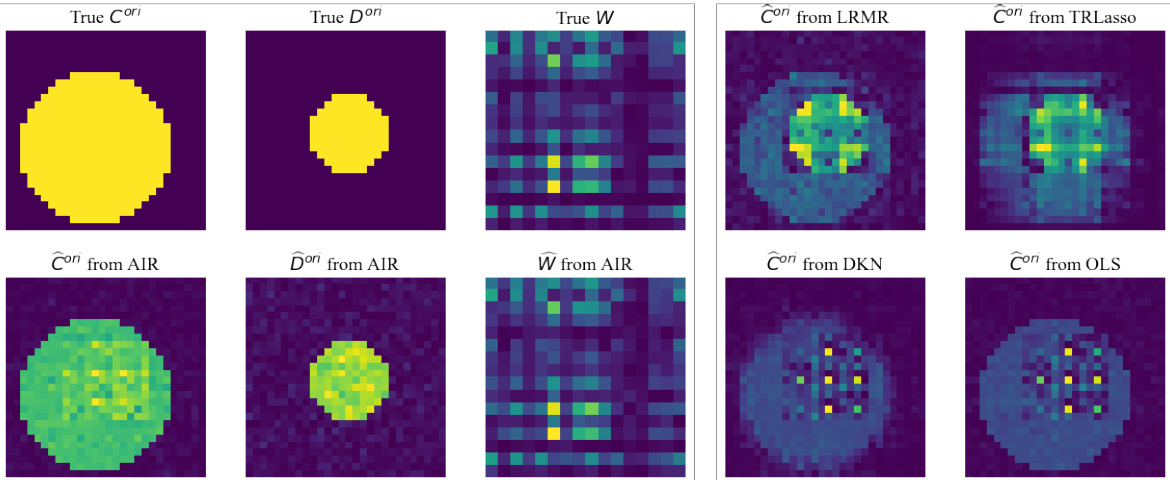
🔼 This figure displays the results of applying the Attention boosted Individualized Regression (AIR) model and other methods to the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset. The left side shows two example brain scans, the corresponding heterogeneous coefficients estimated by AIR, and chord diagrams highlighting significant internal relationships within each brain scan. The right side compares the homogeneous coefficients from AIR to results obtained with other methods.
read the caption
Figure 2: Results on ADNI dataset. (I) Column 1 shows two original samples. Column 2 shows heterogeneous coefficients estimated by AIR. Column 3 presents chord diagrams that illustrate the significant internal relations estimated by AIR. Each coordinate in the chord diagram corresponds to a red box marked in the sample. (II) Columns 4 and 5 compare the homogeneous coefficients estimated by AIR with the coefficients obtained from other methods.
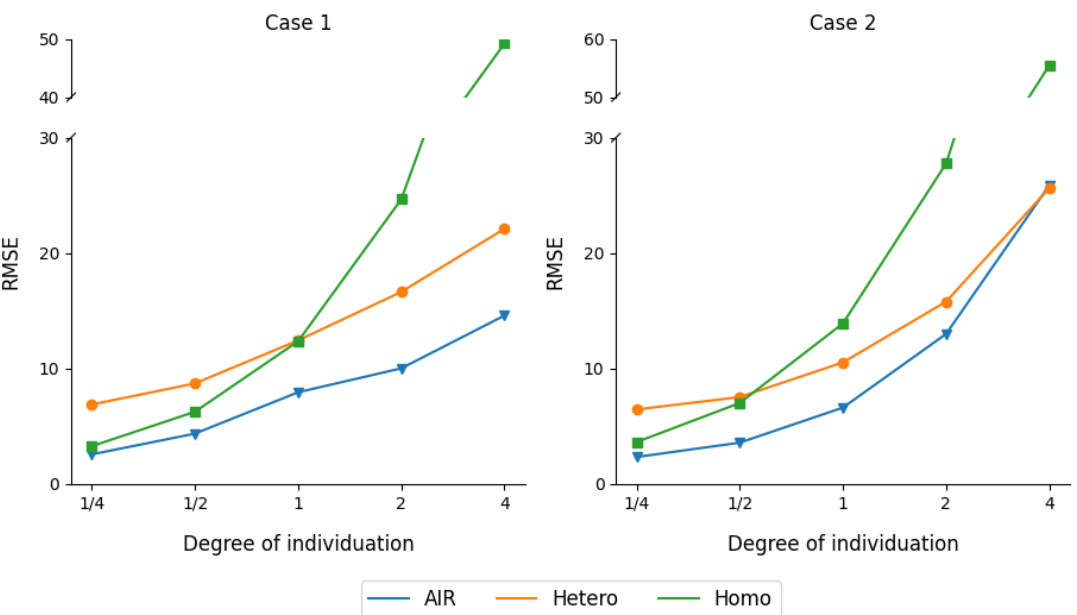
🔼 This figure presents the results of ablation studies comparing three variations of the Attention boosted Individualized Regression (AIR) model: AIR (with both homogeneous and heterogeneous components), Hetero (only the heterogeneous part), and Homo (only the homogeneous part). The experiment was conducted under two conditions (Case 1 and Case 2, differing in how internal relations among image patches were generated), varying the degree of individuation (DI). The plot shows that including both homogeneous and heterogeneous parts leads to the best performance across the range of DI values. In contrast, Homo performs better than Hetero when the data has little to no heterogeneity, while Hetero performs better than Homo when the data has substantial heterogeneity.
read the caption
Figure 3: Results of ablation studies. Incorporating homogeneous part and heterogeneous part makes the AIR more robust, especially better than the one with only heterogeneous part.
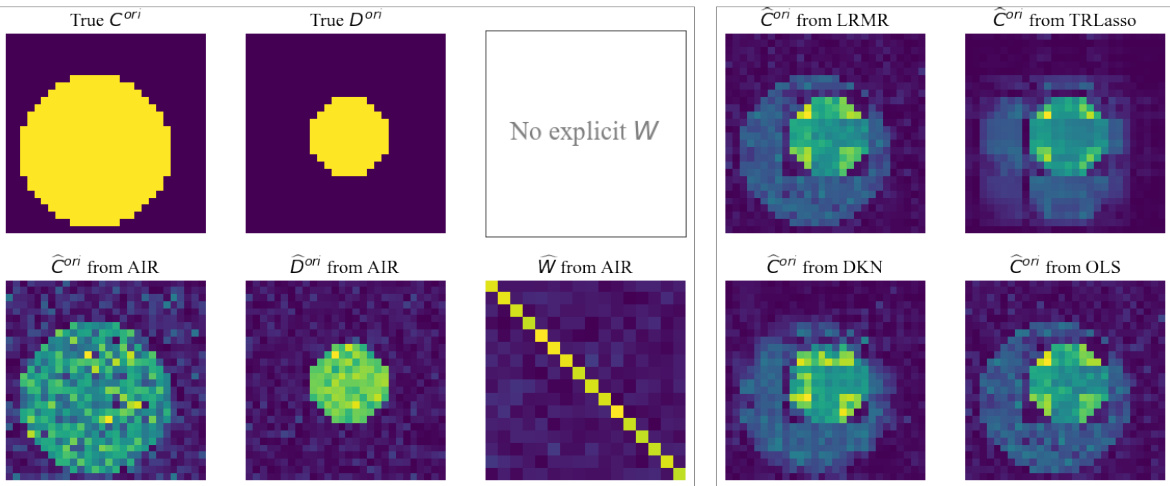
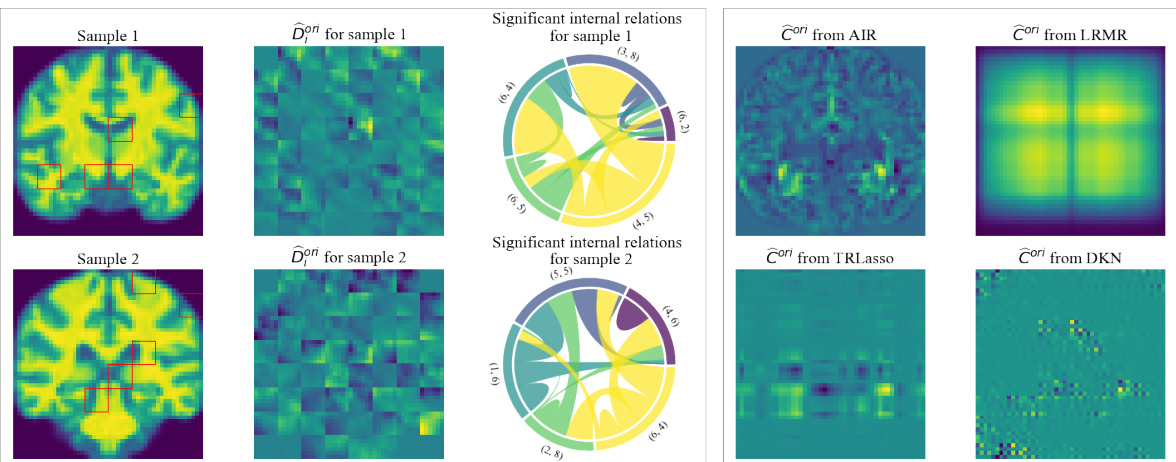
🔼 This figure presents simulation results obtained under Case 2 (without specific W) with DI (degree of individuation) equal to 1.0. It displays the true and estimated coefficient matrices C and D, and the learned weight matrix W from the AIR model, alongside results from other methods (LRMR, TRLasso, DKN, OLS). The key finding is that, even without an explicitly defined W, the AIR model effectively learns a W that approximates a diagonal matrix structure, given the diagonal-like nature of the correlation matrices used in this case.
read the caption
Figure 4: Simulation results under Case 2 with DI = 1.0. There does not exist an explicit true W while the internal relation matrix Ai is computed directly by patchwise Pearson correlation coefficients. Because such Ai is close to a diagonal matrix, it is rational that W from AIR is close to a diagonal matrix.
Full paper#