Learning to Embed Distributions via Maximum Kernel Entropy

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on distribution regression, a rapidly growing area with broad applications. It introduces a novel, unsupervised method for learning data-dependent distribution kernels, addressing a major challenge in the field. This significantly impacts practical applications, as it removes the burden of manual kernel selection and enables data-driven kernel design. The theoretical underpinnings and empirical results open new avenues for future investigation into data-specific kernel learning, potentially revolutionizing various applications in machine learning and beyond.

Visual Insights

#

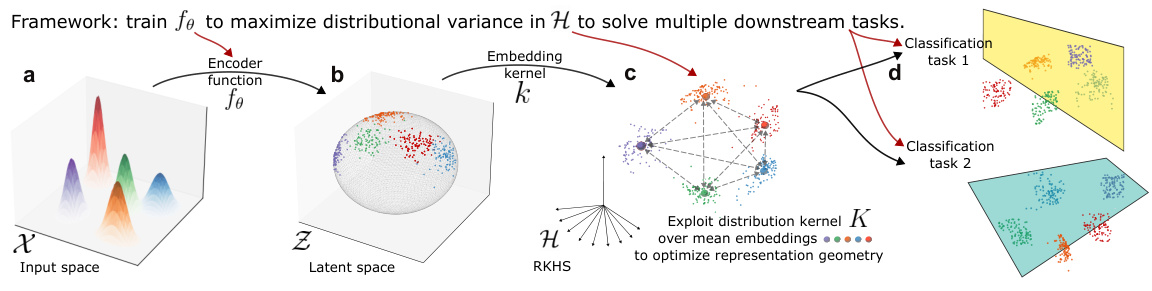
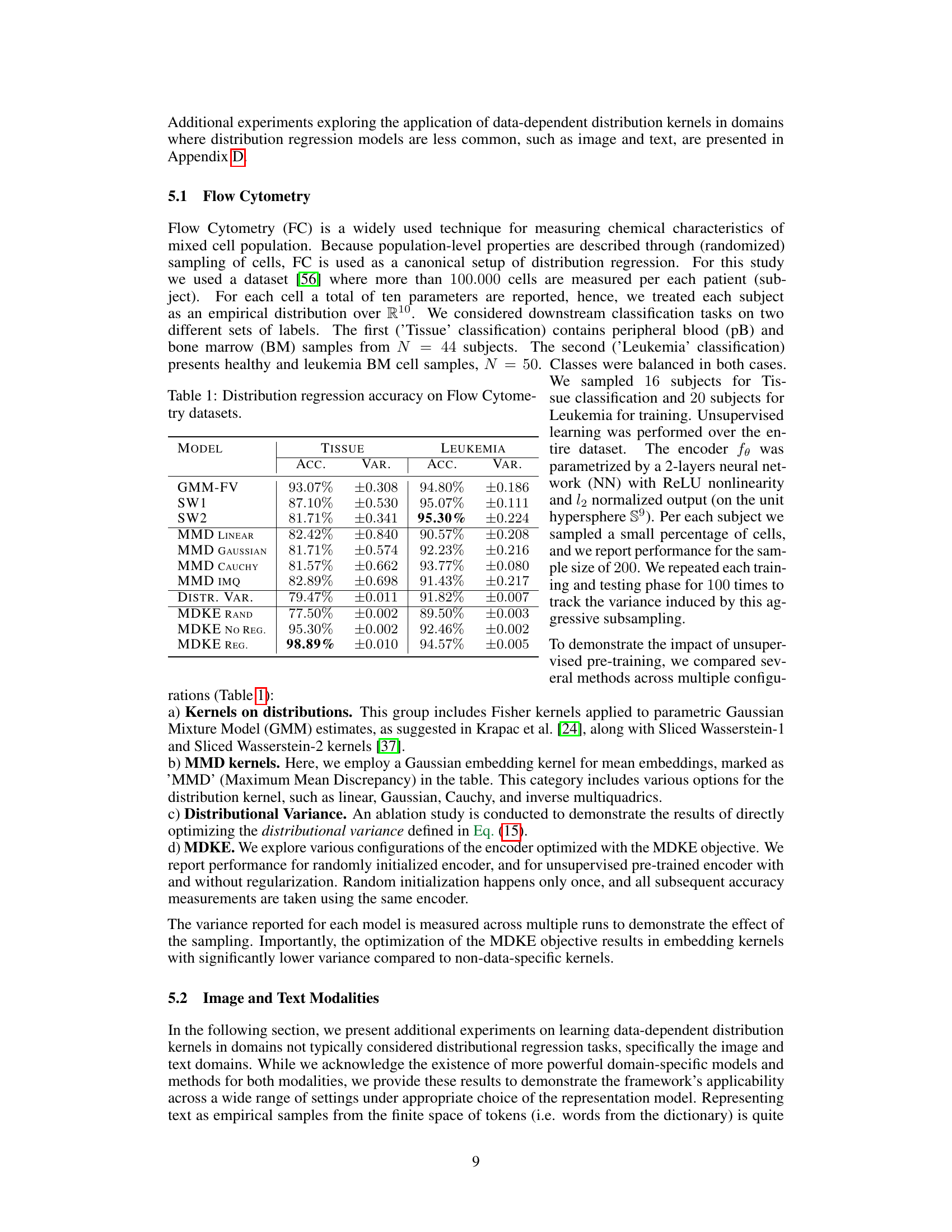
🔼 This figure illustrates the framework for learning to embed distributions. Panel (a) shows example distributions in the input space. The encoder function maps these distributions to a latent space (b) where the distributions are represented as points on a hypersphere. A kernel is used to embed these points into a reproducing kernel Hilbert space (RKHS) (c). Finally, a distribution kernel is used to optimize the representation geometry, allowing for effective classification in multiple downstream tasks (d).

read the caption

Figure 1: Learning to embed distributions. (a) Example of multiple distributions over the input space. (b) The trainable function fe encodes the input dataset into a compact latent space, in our case Z = Sd-1. (c) The first-level embedding kernel k induces kernel mean embedding map to H. The encoder is optimized to maximize the entropy of the covariance operator embedding of the dataset w.r.t. the second-level distribution kernel K between kernel mean embeddings in H. (d) Utilizing learned data-dependent kernel, downstream classification tasks can be solved using tools such as Kernel SVM or Kernel Ridge Regression.

🔼 This table presents the classification accuracy and variance achieved by different models on two flow cytometry datasets: ‘Tissue’ and ‘Leukemia’. The models compared include various kernel methods (GMM-FV, SW1, SW2, MMD with different kernels), a distributional variance baseline, and the proposed MDKE method with and without regularization. The results demonstrate the superior performance of MDKE, especially with regularization, across both datasets.

read the caption

Table 1: Distribution regression accuracy on Flow Cytometry datasets.

In-depth insights

#

Distrib. Regression

#

Distribution regression tackles the challenge of predicting a response variable when the predictor is not a single point, but rather a probability distribution. This is a significant departure from traditional regression methods and requires specialized techniques to handle the inherent complexities of distributions. The core idea is to leverage the properties of the distribution itself, such as its moments or other descriptive statistics, to inform the prediction. A key aspect is the choice of a suitable kernel, often data-dependent, that captures the similarity or distance between distributions. Kernel methods are prominent in this field, enabling the application of well-established algorithms like support vector machines or kernel ridge regression to the space of probability distributions. Despite promising results in various applications, selecting the right kernel remains a crucial and often challenging problem. Recent research has explored learning data-dependent kernels, aiming to build better models that are tailored to specific datasets and thus potentially improve predictive power.

Max Kernel Entropy

#

The concept of “Max Kernel Entropy” suggests a novel approach to learning optimal kernels for distribution regression. It leverages the idea of maximizing entropy in an embedding space to create a data-dependent kernel, avoiding the need for manual kernel selection which is often challenging. The core idea is to embed probability distributions into a feature space where the geometry is learned to be optimal for downstream tasks. This involves an unsupervised learning process, where the entropy of a covariance operator, representing the dataset in the embedding space, is maximized. This maximization is theoretically linked to distributional variance, meaning that maximizing entropy encourages distributions to be well-separated and have low variance. The framework presents a theoretically grounded method for learning data-dependent kernels which addresses the significant challenge of kernel selection in this domain. The method is also applicable across different data modalities, showcasing its flexibility and broader applicability.

Unsupervised Learning

#

The concept of unsupervised learning in the context of this research paper centers on learning a data-dependent distribution kernel without explicit labeled data. This contrasts with supervised methods that rely on labeled examples. The core idea revolves around maximizing the kernel entropy of the dataset’s covariance operator embedding to discover an optimal latent space representation for probability distributions. This approach leverages entropy maximization as a guiding principle, creating a theoretically grounded framework for kernel learning. The resulting data-dependent kernel proves beneficial for various downstream tasks, demonstrating the power of unsupervised techniques to effectively capture the underlying structure of distributional data. The strength lies in the avoidance of arbitrary kernel selection, which is often a major hurdle in applying kernel methods to distribution regression. The unsupervised nature of the learning process is a key advantage, enabling application to scenarios where labeled data is scarce or unavailable.

Modality Experiments

#

A section on “Modality Experiments” in a research paper would ideally delve into the application of a proposed method across diverse data types. This necessitates a multifaceted evaluation strategy. The core would likely involve selecting representative datasets from various modalities (e.g., images, text, sensor readings, time series data). Rigorous experimental design is crucial here, ensuring data splits are appropriate for each modality and that baseline comparison methods are chosen carefully to showcase the method’s relative strengths. Results should be meticulously presented, possibly with tables summarizing performance metrics (accuracy, precision, recall, F1-score, etc.) across different modalities. Visualizations like box plots or bar charts might compare performance across modalities, highlighting any modality-specific advantages or disadvantages of the proposed method. A thorough discussion of the findings would be essential, focusing on patterns observed in the experimental results across modalities. For instance, did the method excel with structured data but falter with unstructured text? Did it perform consistently well across modalities, or were there unexpected performance variations? A comprehensive analysis of these results would demonstrate the generalizability and robustness of the proposed method, enhancing its credibility and potential impact.

Future Directions

#

Future research could explore extending the framework to handle more complex data modalities, such as time series or spatiotemporal data, which would require adapting the kernel design and learning algorithm. Investigating alternative entropy measures beyond the second-order Rényi entropy could reveal more nuanced geometrical properties in the latent embedding space. Furthermore, a more in-depth theoretical analysis of the connection between entropy maximization and distributional variance could lead to improved optimization techniques and a better understanding of the underlying principles. Finally, exploring the use of different kernel types and architectural designs for the encoder network could improve performance and adaptability to various datasets. Incorporating techniques for handling missing data or noisy data is crucial for real-world applications.

More visual insights

#

More on figures

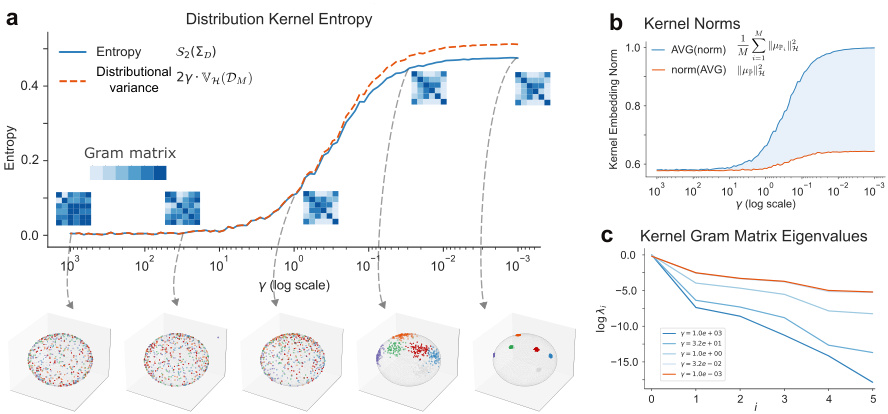
🔼 This figure demonstrates the properties of entropy on a toy example with six distributions arranged on a sphere. Panel (a) shows how entropy and distributional variance change as a function of the distributions’ geometrical arrangement, controlled by the parameter γ. Panel (b) displays the kernel norms that influence the distributional variance bound, showing the relationship between the entropy, kernel norms, and distributional variance. Finally, panel (c) illustrates the effect of γ on the flattening of the Gram matrix eigenvalues.

read the caption

Figure 2: Properties of the entropy on the toy example. (a) Entropy and Distributional Variance for 6 distributions on a sphere as a function of their geometrical arrangement parametrized by γ. (b) Kernel norms that enter the distributional variance bound. The blue shaded area (difference between blue and red lines) corresponds to the dotted red line in (a) (up to multiplicative factor). (c) Flattening of Gram matrix eigenvalues as a function of γ.

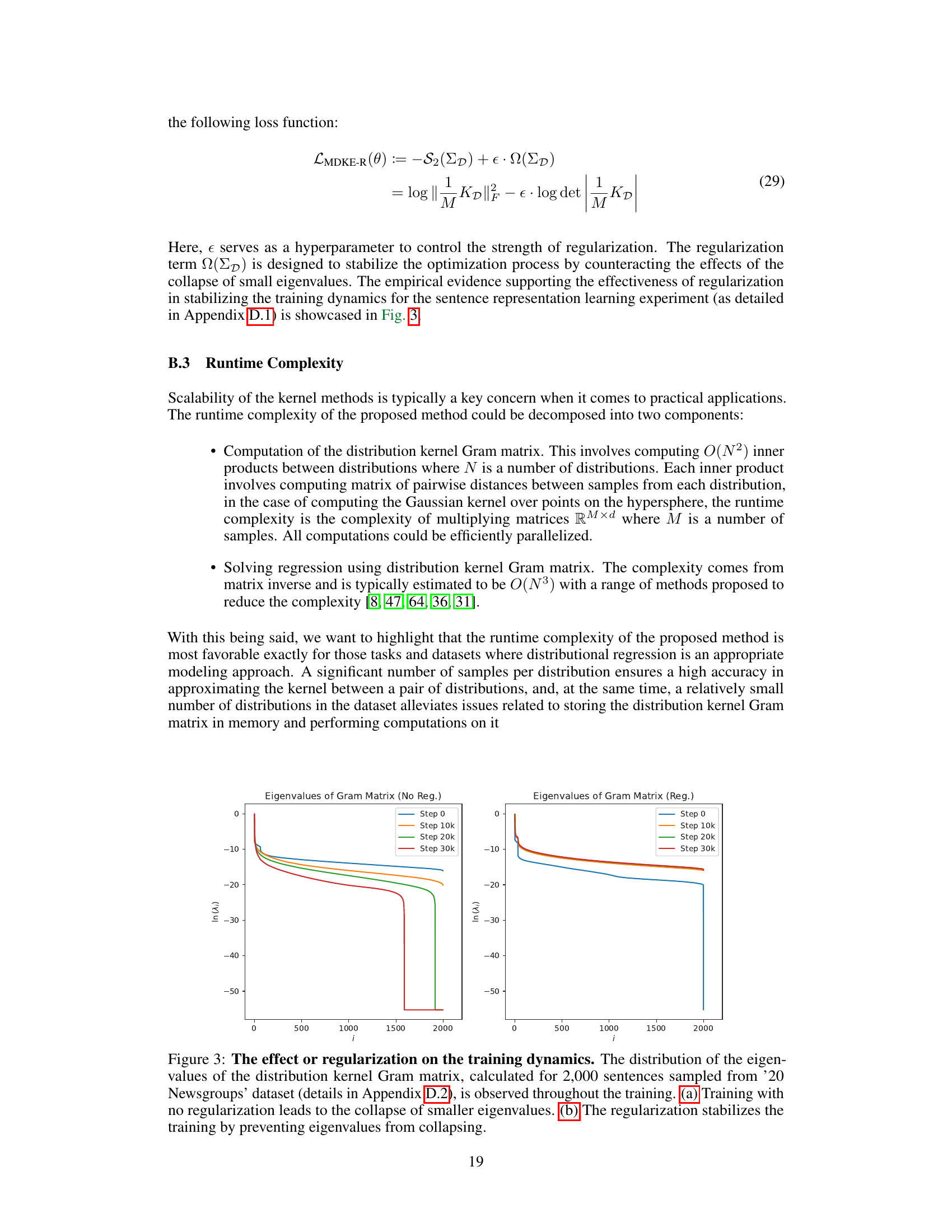
🔼 This figure shows the impact of regularization on eigenvalue distribution during training. The left panel shows the eigenvalues collapsing without regularization, whereas the right panel shows the effect of regularization in preventing this collapse, leading to better training stability.

read the caption

Figure 3: The effect or regularization on the training dynamics. The distribution of the eigenvalues of the distribution kernel Gram matrix, calculated for 2,000 sentences sampled from '20 Newsgroups' dataset (details in Appendix D.2), is observed throughout the training. (a) Training with no regularization leads to the collapse of smaller eigenvalues. (b) The regularization stabilizes the training by preventing eigenvalues from collapsing.

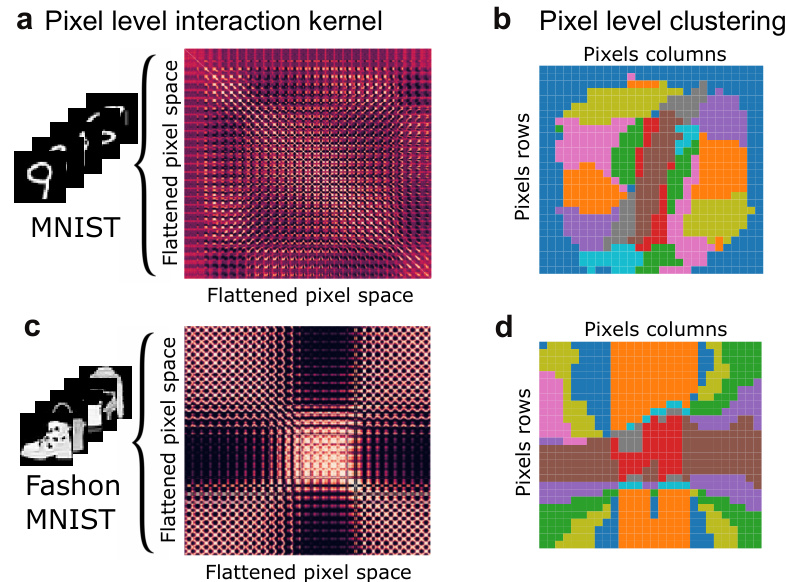
🔼 This figure visualizes the unsupervised learning of image embeddings as finite-support distributions (histograms of pixel intensities). It shows how pixel positions are mapped to points on a hypersphere and optimized using the MDKE objective (Maximum Distribution Kernel Entropy). The figure includes visualizations of the learned pixel-to-pixel interaction kernel Gram matrix and spectral clustering of pixels for both MNIST and Fashion-MNIST datasets.

read the caption

Figure 4: Unsupervised encoding of Images. Unsupervised learning of image embeddings as finite-support distributions (i.e., histograms) of pixel intensities. For every pixel position we assign a point location on the unit hypersphere and optimize such locations via the covariance operator dataset embedding w.r.t. the MDKE objective. (a) Samples from the MNIST dataset and learned pixel-to-pixel interaction kernel Gram matrix. (b) Spectral clustering of pixels based on the learned kernel Gram matrix. (c) and (d) same as (a) and (b) for Fashion-MNIST dataset.

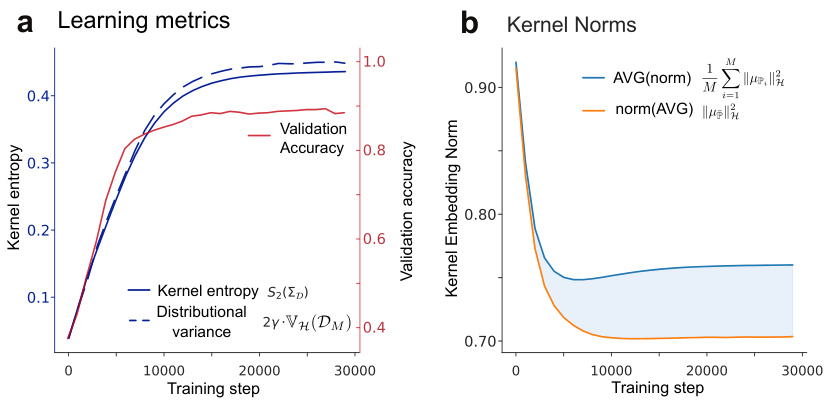
🔼 This figure shows the results of applying the unsupervised learning method to a text dataset. Panel (a) displays the kernel entropy, distributional variance, and validation accuracy over training steps. Panel (b) shows the average kernel norm and the norm of the average embedding over training steps. The shaded blue area in (b) visually represents the difference between the two curves in (a). The figure demonstrates how the proposed method optimizes embeddings by maximizing distributional variance and consequently improving classification accuracy.

read the caption

Figure 5: Unsupervised encoding of Text. Unsupervised learning of sentences embeddings as empirical distributions of words on the '20 Newsgroup' dataset. Goodness of the learned embeddings is evaluated by performing sentence-to-topic classification. (a) Distribution kernel entropy, distributional variance, and validation accuracy throughout training. (b) Kernel norms Eq. (16) throughout training. Shaded blue area (the difference between the blue and red lines) corresponds to the blue dotted line in panel (a) (up to a multiplicative factor).

Full paper

#