↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Self-training, a powerful technique for adapting machine learning models, often struggles when data distributions change (distribution shifts). This is because the model’s confidence in its predictions doesn’t always match its accuracy. Existing solutions involve complex methods that require substantial computational resources.
This paper introduces Anchored Confidence (AnCon), a novel method that leverages temporal consistency to address this issue. AnCon uses a simple, uncertainty-aware ensemble to create smoothed pseudo-labels, improving the selection of reliable pseudo-labels and reducing the impact of noisy ones. The method is shown to be asymptotically correct and empirically achieves substantial performance gains across various distribution shift scenarios, outperforming other state-of-the-art methods without the computational burden.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on self-training and test-time adaptation, especially under distribution shifts. It offers a novel, computationally efficient solution, theoretical guarantees, and addresses a prevalent challenge in machine learning. The method’s robustness and applicability across diverse scenarios open new avenues for improving model adaptability and reliability.
Visual Insights#
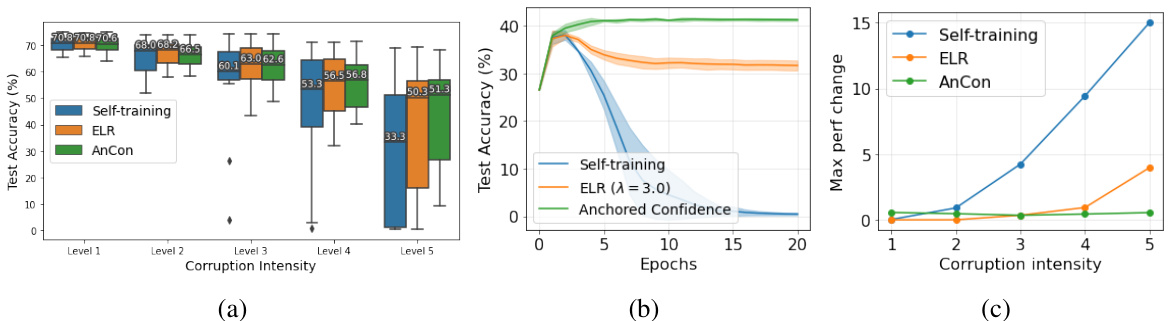
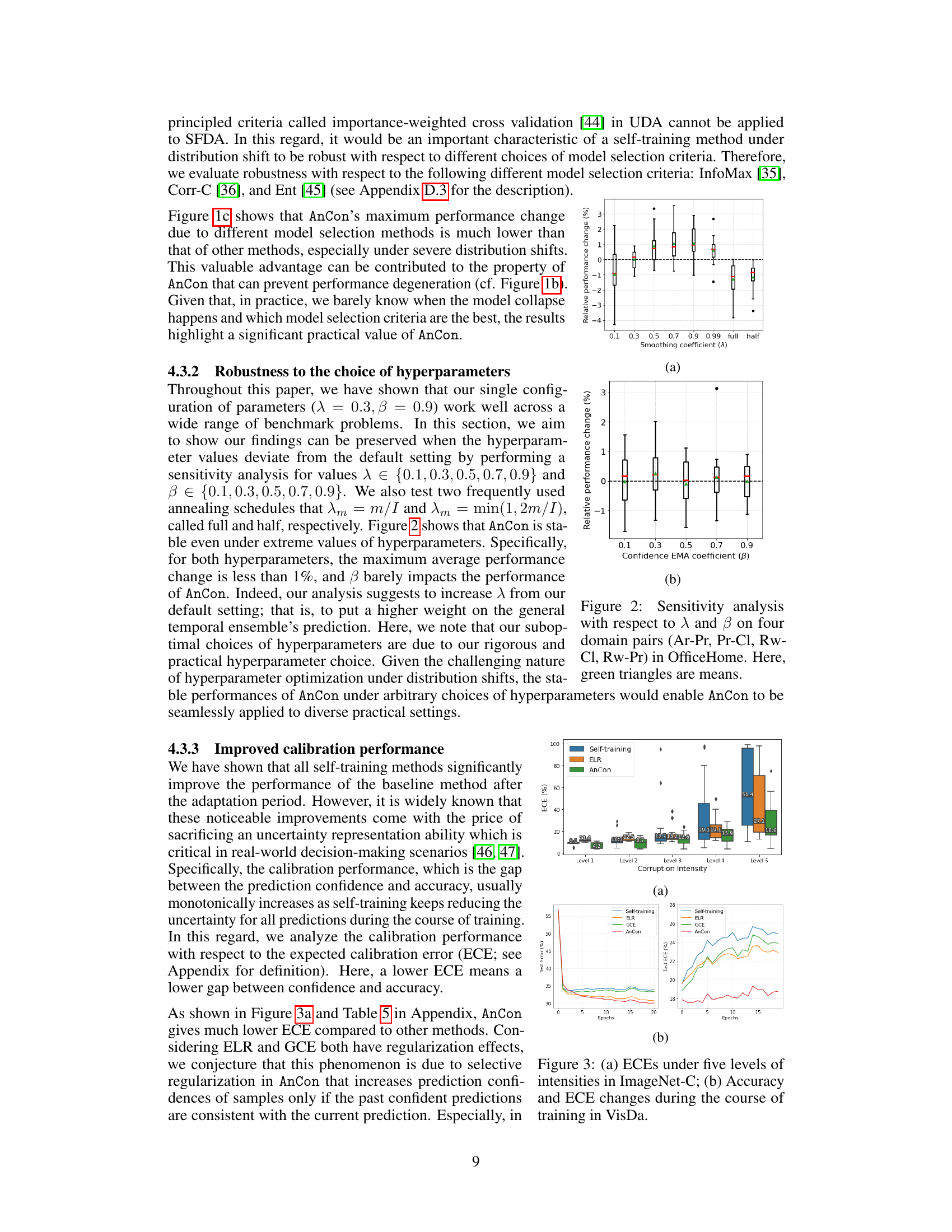
This figure visualizes the results of experiments on ImageNet-C dataset. (a) shows the test accuracy across different corruption intensity levels using three methods: Self-training, ELR, and AnCon. (b) focuses on the defocus blur corruption with intensity level 4 and shows the performance degradation over epochs using the same three methods. (c) displays the maximum performance change among three model selection methods (InfoMax, Corr-C, Ent) across various corruption intensities. The box plots in (a) illustrate the distribution of test accuracy across multiple runs.
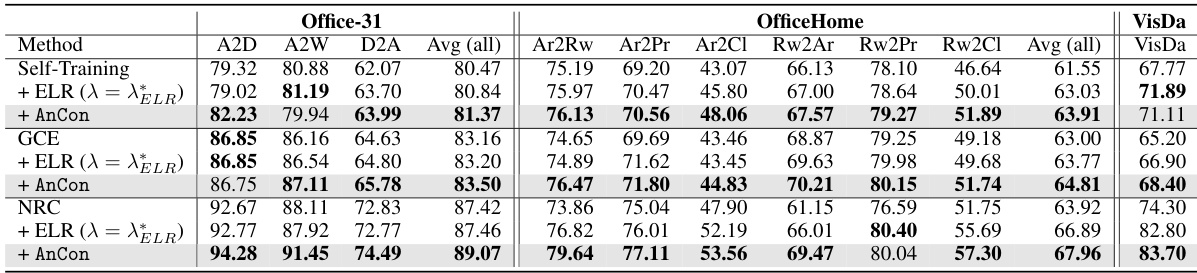
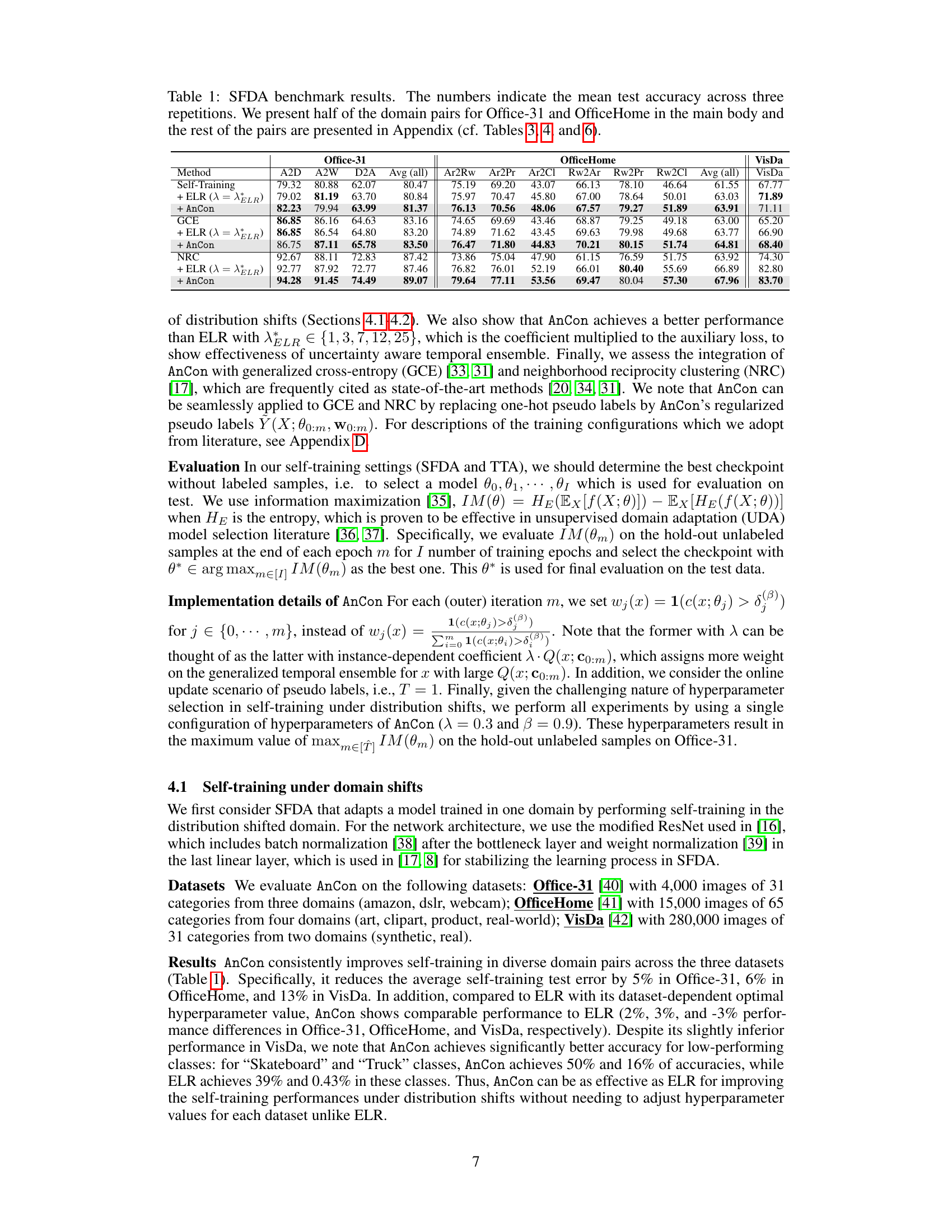
This table presents the results of several self-training methods on three benchmark datasets for source-free domain adaptation (SFDA): Office-31, OfficeHome, and VisDA. The table shows the mean test accuracy across three repetitions for different domain adaptation pairs within each dataset. The methods compared include standard self-training, self-training enhanced with Early Learning Regularization (ELR), self-training with Anchored Confidence (AnCon), Generalized Cross-Entropy (GCE), GCE with ELR, GCE with AnCon, Neighborhood Reciprocity Clustering (NRC), NRC with ELR, and NRC with AnCon. Only a subset of the domain adaptation pairs are shown in the main table; the full results are available in the appendix.
In-depth insights#
AnCon: Temporal Ensembling#
Anchored Confidence (AnCon), employing temporal ensembling, offers a novel approach to enhance self-training’s robustness against distribution shifts. AnCon addresses the core issue of self-training failing under shifts due to the discrepancy between prediction confidence and actual accuracy. Instead of computationally expensive methods like neighborhood-based corrections, AnCon leverages a generalized temporal ensemble that weighs predictions based on their uncertainty. This ensemble smooths noisy pseudo-labels, promoting selective temporal consistency, thereby improving label quality. The method’s theoretical underpinnings demonstrate its asymptotic correctness and ability to reduce the self-training optimality gap. Empirical evaluations showcase AnCon’s consistent improvement (8-16%) across diverse shift scenarios without computational overhead, making it a practical and efficient solution for improving self-training models’ generalization capabilities.
Distribution Shift Focus#
A focus on distribution shift in research signifies the crucial need to address the limitations of machine learning models trained under specific conditions when applied to real-world scenarios with varying data distributions. Robustness and generalization are paramount, demanding methods to improve model performance despite these shifts. The core challenge lies in the discrepancy between predicted confidence and actual accuracy, exacerbated by noisy pseudo-labels in self-training. Addressing this requires strategies that enhance temporal consistency and selective label smoothing, leading to principled and computationally efficient solutions. Theoretical guarantees and extensive empirical evidence across diverse benchmarks demonstrate improved calibration, reduced optimality gaps, and significant performance gains. The research highlights the importance of focusing on temporal consistency and uncertainty-aware ensemble methods to enhance self-training under distribution shifts, addressing the limitations of existing methods. Robustness to hyperparameter choices and model selection criteria further underscores the practical utility of these advancements. This focus signifies a major step toward developing more reliable and adaptable machine learning models for real-world applications.
Theoretical Underpinnings#
The theoretical underpinnings of the research center on the concept of temporal consistency in self-training. The authors demonstrate that by leveraging the temporal ensemble and incorporating anchored confidence, they can improve the accuracy of self-training under distribution shifts. This is supported by theoretical analysis showing that their label smoothing technique can reduce the optimality gap inherent in self-training, and that their proposed method is asymptotically correct. The use of a simple relative thresholding mechanism avoids the computational overhead associated with existing methods. The theoretical framework connects their approach to knowledge distillation, providing further support for the efficacy of their method. The asymptotic optimality of their weighting strategy is proven, emphasizing the robustness and efficiency of their approach in addressing the challenges presented by noisy pseudo labels and distribution shifts.
Robustness & Calibration#
The robustness and calibration of a model are crucial aspects, especially in situations with distribution shifts. Robustness refers to the model’s ability to maintain performance when faced with unexpected inputs or variations in data distribution. A robust model should not be overly sensitive to slight changes in the input data. Calibration, on the other hand, assesses the reliability of the model’s confidence estimates. A well-calibrated model should ideally have a high accuracy rate when it expresses high confidence in its predictions. In the context of distribution shifts, where the test data differs from the training data, both robustness and calibration are essential for reliable performance. A model that is both robust and well-calibrated can be more trusted, especially in critical applications where the confidence level of predictions significantly influences decision-making. Achieving both robustness and calibration is a challenging task that requires careful model design and training strategies. Techniques such as ensemble methods, data augmentation, and proper regularization can enhance robustness. Calibration can be improved through methods that refine the model’s confidence scores, such as Platt scaling or temperature scaling. The synergy between robustness and calibration is particularly relevant when dealing with uncertainty; a robust model may not always provide well-calibrated uncertainty estimates, and vice-versa. Therefore, comprehensive evaluation of both robustness and calibration is vital for assessing and enhancing model reliability, particularly in real-world scenarios where distribution shifts are inevitable.
Future Research Scope#
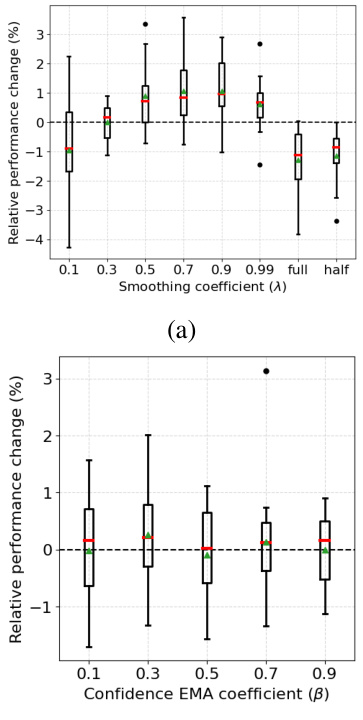
The research paper’s core contribution is AnCon, a novel method enhancing self-training’s robustness against distribution shifts. Future research could explore several promising avenues. First, adaptively determining the optimal smoothing parameter (λ) in AnCon, currently fixed, would enhance its performance. Investigating alternative weighting schemes beyond simple relative thresholding could unlock further improvements. The paper hints at the possibility of combining local and temporal consistency; exploring this would be highly valuable. Extending AnCon to sequential decision-making, a more complex scenario, presents a significant but potentially rewarding challenge, requiring careful consideration of rewards and exploration strategies. Finally, a deeper investigation into the theoretical underpinnings of AnCon, particularly concerning its assumptions and their impact on performance, could yield significant insights and improvements.
More visual insights#
More on figures
This figure visualizes the results of experiments on ImageNet-C dataset. (a) shows the test accuracy for different corruption intensity levels. (b) focuses on the performance degradation of defocus blur with intensity 4. (c) displays the maximum performance changes under various model selection methods, highlighting the robustness of AnCon.

This figure shows the results of experiments conducted to evaluate the performance of different methods under various conditions. Panel (a) presents the test accuracy for ImageNet-C dataset across five different corruption intensity levels and shows the robustness of AnCon. Panel (b) focuses specifically on the defocus blur corruption with intensity 4, highlighting the performance degradation of various methods. Panel (c) illustrates the robustness of AnCon against different model selection methods.
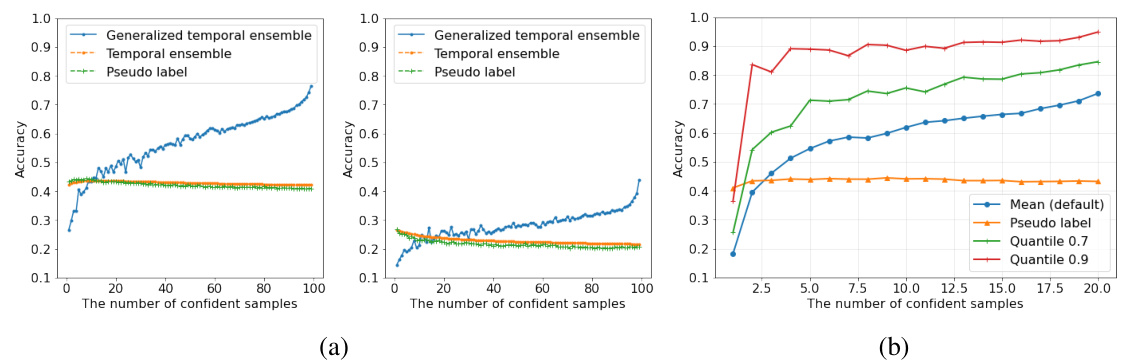
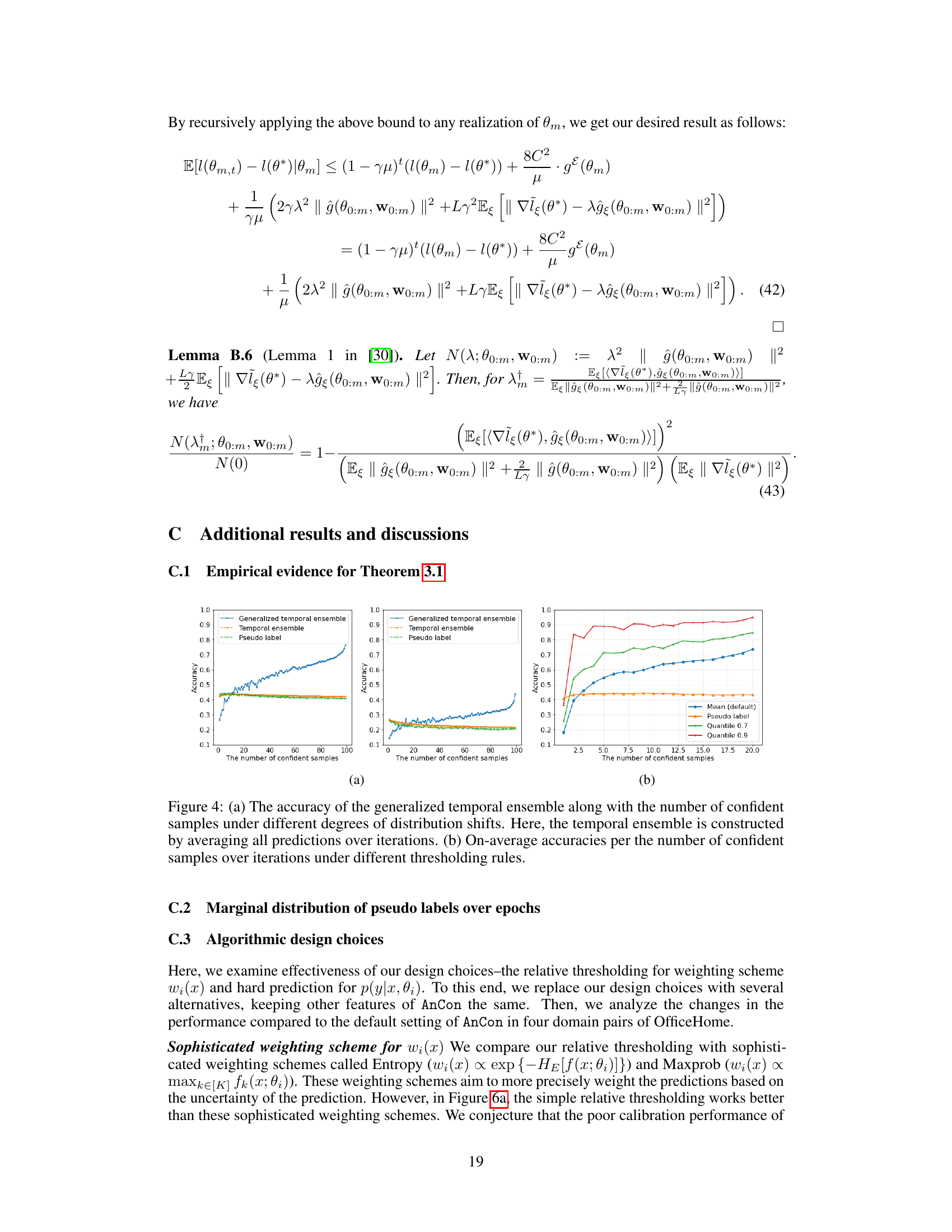
This figure shows the accuracy of different ensemble methods (generalized temporal ensemble and temporal ensemble) compared to using only pseudo labels. The x-axis represents the number of confident samples, and the y-axis represents accuracy. Subfigure (a) demonstrates the accuracy under varying degrees of distribution shifts, while subfigure (b) shows the impact of different thresholding rules on the average accuracy.

This figure shows three subfigures. (a) shows the test accuracy for each intensity level in ImageNet-C dataset for different methods such as self-training, ELR, and AnCon. (b) shows the performance degeneration in the defocus blur corruption with intensity 4. (c) shows the maximum performance changes under different model selection methods. The box plots show the distribution of the results, with the median, interquartile range, and whiskers representing the central tendency and variability of the data.
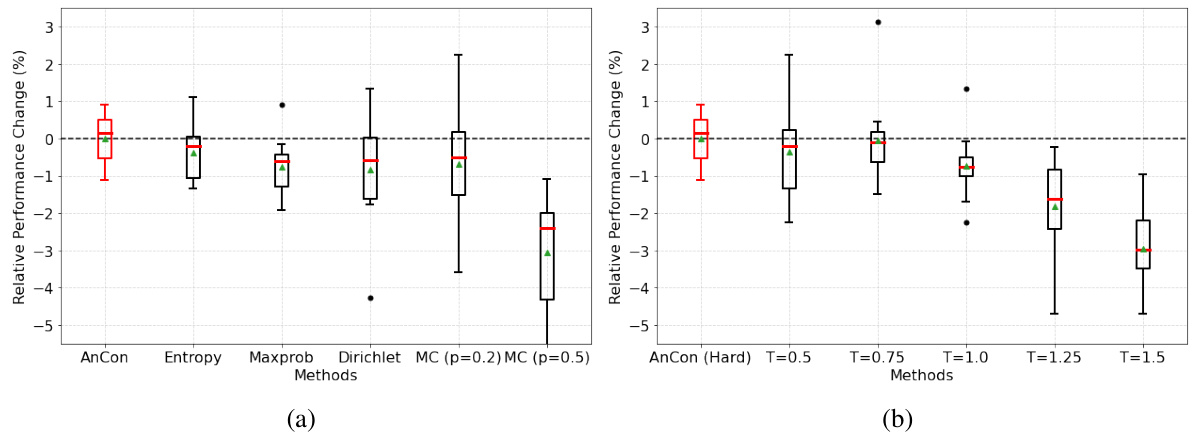
This ablation study investigates the impact of different weighting schemes (AnCon, Entropy, Maxprob, Dirichlet) and prediction methods (AnCon (Hard), different softmax temperature values) on the self-training performance. The box plots show relative performance changes compared to the default AnCon method, across various datasets and distribution shifts. The results demonstrate that the default choices of AnCon for weighting and prediction yield superior performance compared to alternatives.
More on tables

This table presents the results of several self-training methods on three domain adaptation benchmark datasets: Office-31, OfficeHome, and VisDA. The methods compared include standard self-training, self-training with early learning regularization (ELR), self-training with Anchored Confidence (AnCon), Generalized Cross Entropy (GCE), GCE with ELR, GCE with AnCon, Neighborhood Reciprocity Clustering (NRC), NRC with ELR, and NRC with AnCon. The table shows the mean test accuracy across three repetitions for various source and target domain pairs within each dataset. Only a subset of the domain pairs are shown in the main table, with the rest provided in the appendix.
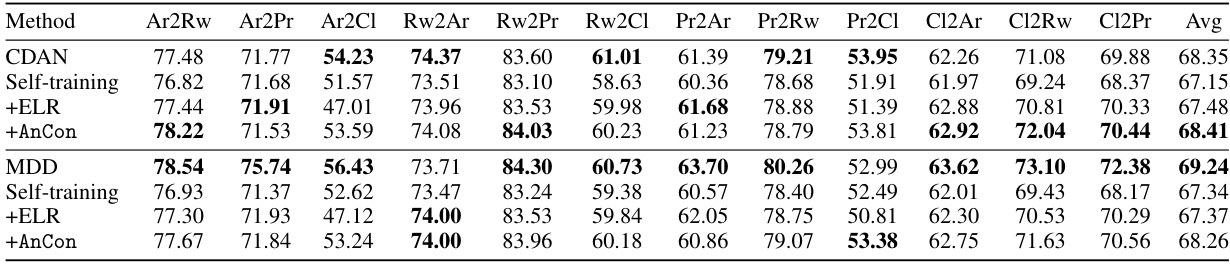
This table presents the results of several self-training methods on three popular domain adaptation benchmark datasets: Office-31, OfficeHome, and VisDA. The table shows the average test accuracy across three repetitions for each method and dataset. The methods compared include vanilla self-training, self-training with ELR (Early Learning Regularization), self-training with AnCon (Anchored Confidence), GCE (Generalized Cross-Entropy), and NRC (Neighborhood Reciprocity Clustering), often combined with ELR and AnCon. Only a subset of domain pairs is shown in the main table for Office-31 and OfficeHome, with the remaining results located in the appendix.

This table presents the results of several self-training methods on three benchmark datasets for source-free domain adaptation (SFDA). The table shows the average test accuracy across three repetitions for different combinations of source and target domains. It compares the vanilla self-training method with the addition of Early Learning Regularization (ELR) and the proposed Anchored Confidence (AnCon) method. The results also include the performance of Generalized Cross-Entropy (GCE) and Neighborhood Reciprocity Clustering (NRC) methods, both with and without ELR and AnCon.

This table presents the results of source-free domain adaptation (SFDA) experiments on three benchmark datasets: Office-31, OfficeHome, and VisDA. The table shows the mean test accuracy across three repetitions for several methods including self-training, self-training with early learning regularization (ELR), self-training with anchored confidence (AnCon), generalized cross-entropy (GCE), GCE+ELR, GCE+AnCon, neighborhood reciprocity clustering (NRC), NRC+ELR, and NRC+AnCon. Only half of the domain pairs for Office-31 and OfficeHome are shown in the main body of the paper; the remaining results are in the appendix.

This table presents the results of several self-training methods on three benchmark datasets for source-free domain adaptation (SFDA): Office-31, OfficeHome, and VisDA. The table shows the mean test accuracy across three repetitions for various domain adaptation pairs. A subset of the domain pairs are shown in the main paper, with the remainder in the appendix. The methods compared include vanilla self-training, self-training with early learning regularization (ELR), self-training with the proposed Anchored Confidence (AnCon) method, Generalized Cross Entropy (GCE), GCE with ELR, GCE with AnCon, Neighborhood Reciprocity Clustering (NRC), NRC with ELR, and NRC with AnCon.
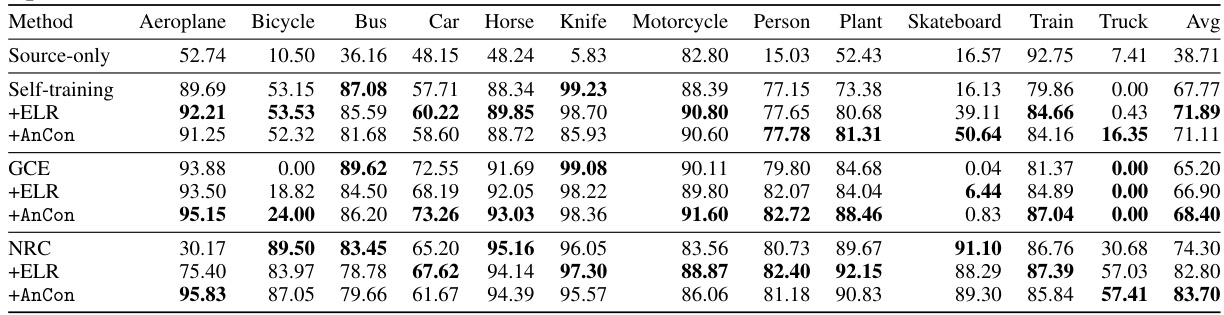
This table presents the results of several self-training methods on three benchmark datasets for source-free domain adaptation (SFDA): Office-31, OfficeHome, and VisDA. The table shows the mean test accuracy across three repetitions for each method. Only a subset of domain pairs are displayed in the main table, with the rest available in the appendix. The methods compared include standard self-training, self-training with early learning regularization (ELR), self-training with anchored confidence (AnCon), generalized cross-entropy (GCE), GCE with ELR, GCE with AnCon, neighborhood reciprocity clustering (NRC), NRC with ELR, and NRC with AnCon.

This table presents the results of several self-training methods on three different datasets (Office-31, OfficeHome, and VisDA) under different domain shift scenarios. It compares the performance of standard self-training with the proposed AnCon method, along with ELR and other state-of-the-art techniques. The table shows mean test accuracy across three repetitions. Only a selection of domain pairs are shown in the main paper, with the rest provided in the appendix.

This table presents the results of several self-training methods on three benchmark datasets for source-free domain adaptation (SFDA): Office-31, OfficeHome, and VisDA. The table shows the average test accuracy across three repetitions for each method on various domain adaptation tasks. Half of the domain pairs for Office-31 and OfficeHome are shown in the main paper, with the remaining pairs provided in the appendix. The methods compared include vanilla self-training, self-training enhanced with early learning regularization (ELR), self-training with the proposed Anchored Confidence (AnCon) method, generalized cross-entropy (GCE), GCE with ELR, GCE with AnCon, neighborhood reciprocity clustering (NRC), NRC with ELR, and NRC with AnCon. The table demonstrates the performance improvements achieved by AnCon compared to other methods.

This table presents the results of several self-training methods on three different datasets (Office-31, OfficeHome, VisDA) under source-free domain adaptation (SFDA) settings. It shows the mean test accuracy across three repetitions for each method, including vanilla self-training, self-training with early learning regularization (ELR), self-training with Anchored Confidence (AnCon), Generalized Cross-Entropy (GCE), GCE+ELR, GCE+AnCon, Neighborhood Reciprocity Clustering (NRC), NRC+ELR, and NRC+AnCon. Only a subset of domain pairs are shown in the main table, with the remaining pairs detailed in the appendix.

This table presents the results of several self-training methods on three standard domain adaptation benchmark datasets: Office-31, OfficeHome, and VisDA. For each dataset, several different source and target domain pairs are tested, and the mean test accuracy across three repetitions is reported for each method. The methods compared include vanilla self-training, self-training with early learning regularization (ELR), self-training with the proposed Anchored Confidence (AnCon) method, Generalized Cross-Entropy (GCE), GCE with ELR, GCE with AnCon, Neighborhood Reciprocity Clustering (NRC), NRC with ELR, and NRC with AnCon. The table shows the significant performance improvement achieved by AnCon in comparison to the other methods, especially under challenging distribution shifts.

This table presents the results of several self-training methods on three benchmark datasets for source-free domain adaptation (SFDA): Office-31, OfficeHome, and VisDA. The table shows the average test accuracy across three repetitions for different domain adaptation tasks within each dataset. The methods compared include standard self-training, self-training enhanced with early learning regularization (ELR), self-training with the proposed Anchored Confidence (AnCon) method, generalized cross-entropy (GCE), GCE with ELR, GCE with AnCon, neighborhood reciprocity clustering (NRC), NRC with ELR, and NRC with AnCon. Only a subset of the domain pairs for Office-31 and OfficeHome are shown in the main table; the complete results are in the appendix.
Full paper#