Tri-Level Navigator: LLM-Empowered Tri-Level Learning for Time Series OOD Generalization

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it tackles the challenging problem of out-of-distribution (OOD) generalization in time series, a crucial area with limited existing research. It introduces a novel tri-level learning framework (TTSO) that considers both sample-level and group-level uncertainties, offering a fresh theoretical perspective. The proposed stratified localization algorithm efficiently solves the tri-level optimization problem, and experiments demonstrate significant performance improvements on real-world datasets. Furthermore, the integration of pre-trained LLMs provides a powerful new tool for time series analysis. This research opens avenues for improved robustness and adaptability in machine learning models applied to time-series data, which is highly relevant given the increasing prevalence of time-series data across various domains.

Visual Insights

#

This figure illustrates three scenarios of uncertainties in data distributions. (1) sample-level: shows individual data points scattered around the decision boundary, representing sample-level uncertainty. (2) group-level: shows clusters of data points, each cluster representing a group. The decision boundary separates the groups, indicating group-level uncertainty. (3) both: combines both sample-level and group-level uncertainties, showing a more complex and realistic distribution.

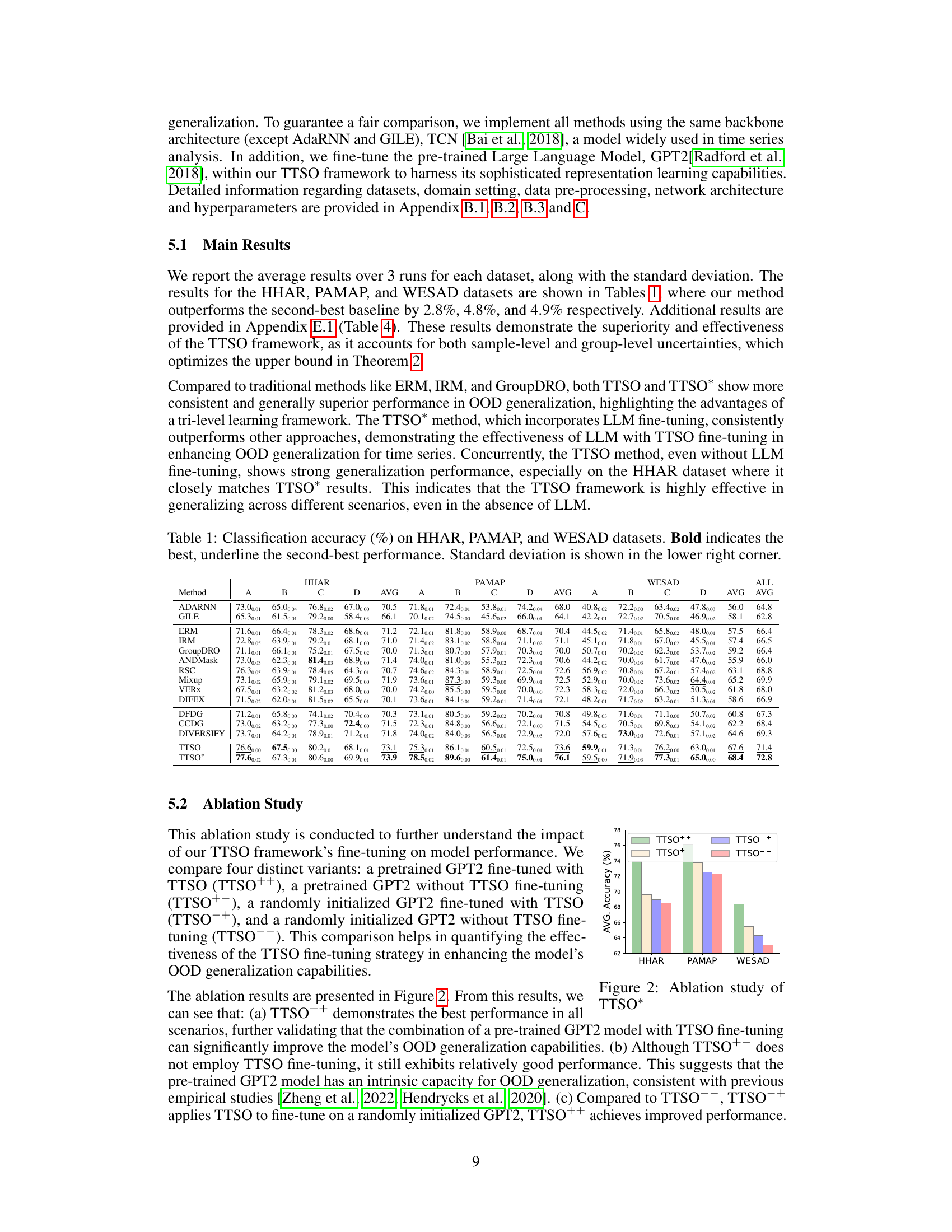
This table presents the classification accuracy of different methods on three time series datasets: HHAR, PAMAP, and WESAD. The accuracy is presented as a percentage, with the best performance in bold and the second-best underlined. Standard deviations are included to show the variability in the results. The table allows for a comparison of the proposed TTSO and TTSO* methods against several baseline and state-of-the-art OOD generalization techniques.

In-depth insights

#

Tri-Level Learning

#

The concept of “Tri-Level Learning” in the context of time series out-of-distribution (OOD) generalization presents a novel approach to address the multifaceted challenges inherent in this domain. It suggests a hierarchical learning framework that simultaneously tackles sample-level and group-level uncertainties, a significant advancement over existing methods that often focus on only one type of uncertainty. The tri-level structure likely involves an outer level optimizing overall model performance, a middle level optimizing data grouping to handle group-level variations, and an inner level focused on sample-specific uncertainties. This integrated approach is theoretically well-motivated, offering a fresh perspective on OOD generalization. The authors may also propose a specific algorithm for optimizing this tri-level structure. A key strength of this approach is its potential to learn more robust and generalizable representations than traditional methods. However, the complexity of a tri-level optimization and the algorithm required to solve it could be substantial, representing a major hurdle in implementation. The successful application of this method would be a substantial contribution to the field, potentially leading to significant improvements in time series models’ ability to generalize to unseen data.

LLM-TTSO Framework

#

The LLM-TTSO framework presents a novel approach to time series out-of-distribution (OOD) generalization by integrating pre-trained Large Language Models (LLMs) with a tri-level learning structure. This framework addresses both sample-level and group-level uncertainties, a unique aspect not found in conventional methods. The tri-level optimization, involving model parameter learning, dynamic data regrouping, and data augmentation, is tackled by a stratified localization algorithm. This innovative approach contrasts with traditional gradient-based methods and is theoretically demonstrated to offer guaranteed convergence. LLMs enhance the robustness of the learned representations. Fine-tuning these models using the TTSO framework leads to significant improvements in performance, showcasing the power of combining LLMs’ advanced reasoning capabilities with a sophisticated OOD generalization strategy. The framework is thoroughly evaluated using real-world datasets and ablation studies demonstrating its efficacy.

Stratified Localization

#

The concept of “Stratified Localization” suggests a novel approach to solving complex, hierarchical optimization problems, particularly within the context of out-of-distribution (OOD) generalization. It appears to be a multi-level strategy addressing sample-level and group-level uncertainties simultaneously, avoiding the computational burden of traditional gradient-based methods that struggle with nested optimization. This is achieved through a stratified approach, where the problem is decomposed into simpler sub-problems. The algorithm likely uses cutting planes to approximate the feasible region at each level, iteratively refining the solution. This decomposition allows for a more efficient search for the optimal parameters, making the method computationally feasible, especially when dealing with high-dimensional data. The theoretical analysis of its convergence rate and iteration complexity is also important, suggesting a well-founded and efficient method that offers a significant improvement over current techniques for handling complex, multi-level optimization challenges.

OOD Generalization

#

Out-of-Distribution (OOD) generalization is a crucial area in machine learning focusing on model robustness when encountering unseen data differing significantly from training data. Time series OOD generalization poses unique challenges due to temporal dependencies and dynamic patterns. Existing approaches often focus solely on sample-level or group-level uncertainties, neglecting the interplay between them. Novel frameworks aim to address this gap by incorporating both levels of uncertainty within a unified learning strategy, leading to improved model adaptability and resilience. Tri-level learning offers a promising solution, incorporating sample-level, group-level uncertainties, and optimal parameter learning. This approach theoretically guarantees convergence, achieving improved performance in real-world time series OOD generalization tasks, notably when combined with Large Language Models (LLMs). The LLM’s advanced pattern recognition capabilities, when fine-tuned using the tri-level framework, significantly enhance OOD robustness, highlighting the potential of foundational models in this challenging domain.

Future Directions

#

Future research could explore extending the tri-level learning framework to other time series tasks like forecasting and anomaly detection. Investigating the framework’s performance on diverse time series data with varying characteristics (e.g., length, dimensionality, noise levels) would be crucial. Furthermore, a comparative study against other state-of-the-art OOD generalization methods on a broader range of datasets would solidify its capabilities and limitations. Exploring different LLM architectures and fine-tuning strategies to further optimize the TTSO framework’s effectiveness and efficiency is warranted. Analyzing the trade-off between the model’s robustness, computational cost, and convergence rate should be a key focus. Finally, developing a more comprehensive theoretical analysis to better understand the generalization properties of TTSO, and potentially applying it to other data modalities, would broaden its applicability.

More visual insights

#

More on figures

This ablation study compares four variants of the TTSO framework to understand the impact of pre-trained LLMs and TTSO fine-tuning on model performance. The four variants are: (1) TTSO++, a pretrained GPT2 model fine-tuned with TTSO; (2) TTSO+-, a pretrained GPT2 model without TTSO fine-tuning; (3) TTSO-+, a randomly initialized GPT2 model fine-tuned with TTSO; and (4) TTSO–, a randomly initialized GPT2 model without TTSO fine-tuning. The results show the average accuracy for each variant across three datasets (HHAR, PAMAP, WESAD).

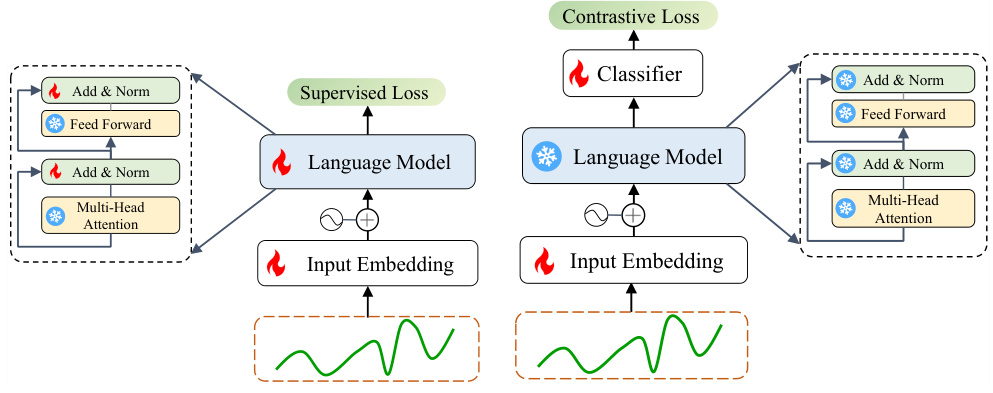
This figure shows the architecture used for fine-tuning LLMs with the TTSO framework. The process is broken into two stages. In the first stage (alignment fine-tuning), the input time series data is passed through an input embedding layer into a language model. A contrastive loss is used during training. The second stage (downstream fine-tuning) uses the output of the language model as input to a classifier which is trained using a supervised loss. This two-stage approach helps adapt the LLM to the specific time series classification task while retaining the knowledge learned during pre-training.

This figure illustrates the concept of sample-level uncertainty in time series data. Each line represents a short segment of time series data points with the same label, highlighting the variability within a single class. The variations between the lines, even though they all belong to the same class, show the inherent noise and fluctuations present at the sample level. This is in contrast to group-level uncertainty, which is not shown in this figure but refers to differences between groups or classes.

This figure demonstrates the group-level uncertainty by displaying the distribution of x-axis values from the accelerometer across different groups (users). Each color represents a distinct group, and each group’s unique characteristics contribute to the overall group-level uncertainty.

This figure shows the impact of the number of Transformer layers in a GPT-2 model on the average accuracy of out-of-distribution (OOD) generalization across three different datasets: HHAR, PAMAP, and WESAD. The x-axis represents the number of Transformer layers (k), and the y-axis represents the average accuracy. The plot allows for a comparison of the performance across the three datasets as the number of layers changes. It helps to determine the optimal number of layers to achieve the best OOD generalization performance.

More on tables

This table presents the classification accuracy achieved by various methods (including the proposed TTSO and TTSO* methods) on three different datasets: HHAR, PAMAP, and WESAD. The accuracy is expressed as a percentage, and the best-performing method for each dataset is indicated in bold, while the second-best is underlined. Standard deviations are also provided to show the variability of the results.

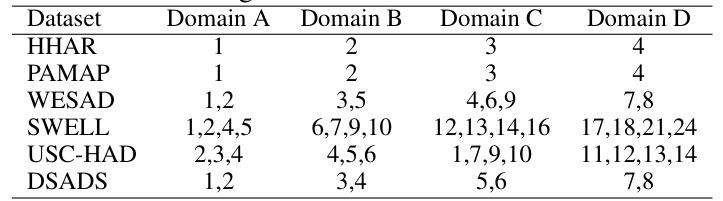
This table shows the domain split strategy used for the HHAR, PAMAP, and WESAD datasets in the experiments. Each dataset is divided into four domains (A, B, C, and D), with specific classes assigned to each domain. This ensures a balanced representation of classes across domains, allowing for a more robust evaluation of the model’s out-of-distribution generalization capabilities. The distribution of classes aims to be similar for different domains.

This table presents the classification accuracy achieved by various methods on three different datasets (HHAR, PAMAP, and WESAD). The accuracy is presented as a percentage, with the standard deviation shown in the lower right corner of each cell. Bold font highlights the best-performing method for each dataset and domain, while underlined font indicates the second-best performer. The table allows for comparison of the proposed TTSO method against several baseline and state-of-the-art OOD generalization methods for time series data.

This table presents the classification accuracy achieved by various methods (including the proposed TTSO and TTSO* models) on three benchmark time series datasets (HHAR, PAMAP, and WESAD). The results highlight the superior performance of TTSO and especially TTSO*, demonstrating the benefit of incorporating LLMs. Standard deviations are included to show result variability.

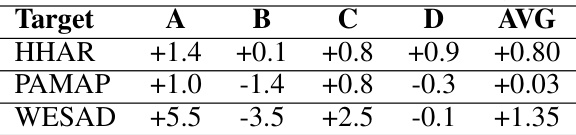
This table presents the performance improvement achieved by the TTSO framework across different domains for three datasets: HHAR, PAMAP, and WESAD. Each row represents a target dataset (HHAR, PAMAP, or WESAD), and each column shows the percentage change in accuracy for that target dataset when trained on a specific source domain (A, B, C, or D). The ‘AVG’ column represents the average improvement across all source domains for each target dataset.

Full paper

#