TL;DR#
The increasing number and size of machine learning models pose significant challenges for evaluation, particularly when dealing with continually expanding benchmarks. Repeated testing of numerous models across vast datasets leads to substantial computational costs, hindering the progress of research. This paper addresses this critical issue by focusing on the high cost of evaluating a growing number of models against ever-expanding test samples.
The proposed solution, called Sort & Search, uses dynamic programming algorithms to strategically select test samples for evaluating new models. This intelligent selection process significantly reduces computation time, achieving up to a 1000x reduction while maintaining accuracy. It also provides valuable insights into the limitations of current accuracy prediction metrics, suggesting a need to move towards sample-level evaluation for improved results and enhanced understanding. The framework introduced is highly scalable, and further analysis of the method’s errors reveals valuable implications for future research in model evaluation and benchmark design.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers tackling the challenges of evaluating increasingly large and complex machine learning models. It offers a highly efficient and scalable solution, addressing a critical bottleneck in the field. The proposed method, Sort & Search, significantly reduces computational costs associated with model evaluation while maintaining high accuracy. This advancement opens up new avenues of research into lifelong model evaluation, improving the efficiency of evaluating ever-expanding benchmarks and facilitating faster progress in the field.
Visual Insights#

🔼 This figure illustrates the core idea of the Sort & Search method. The left side shows the initial state: a set of ’n’ samples and ’m’ models, with their accuracy predictions stored in a matrix. The top-right shows how a new model is efficiently evaluated using a subset of samples (’n’’). The bottom-right demonstrates how a new sample is efficiently added to the benchmark by determining its difficulty using a subset of models (’m’).
read the caption
Figure 1: Efficient Lifelong Model Evaluation. Assume an initial pool of n samples and m models evaluated on these samples (left). Our goal is to efficiently evaluate a new model (insertM) at sub-linear cost (right top) and efficiently insert a new sample into the lifelong benchmark (insertD) by determining sample difficulty at sub-linear cost (right bottom). See Section 2 for more details.
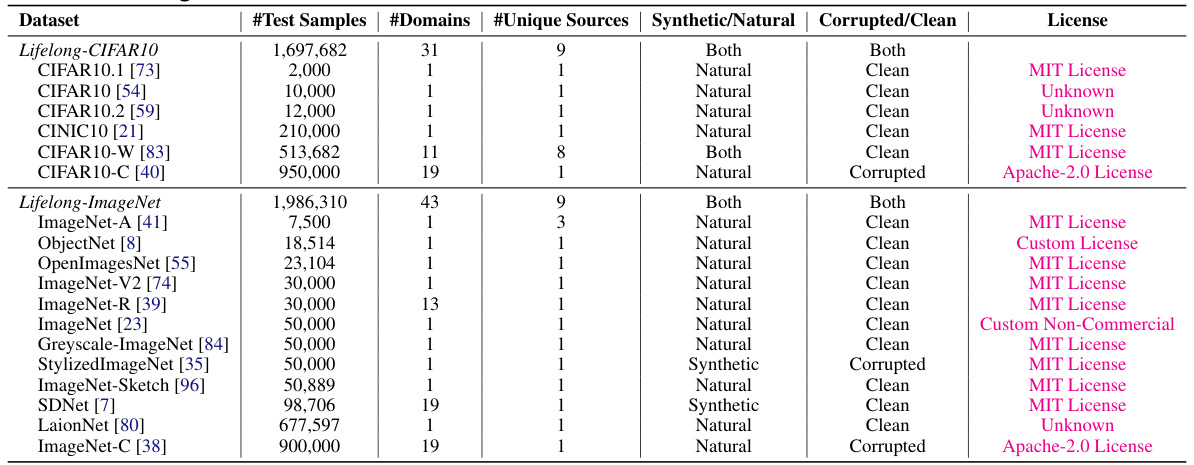
🔼 This table presents a detailed breakdown of the datasets used to create the Lifelong-CIFAR10 and Lifelong-ImageNet benchmarks. It lists each constituent dataset, the number of test samples, the number of domains represented, the number of unique sources, whether the data is synthetic or natural, if it has been corrupted, the license associated with the dataset and the benchmark it contributes to. This information helps to understand the composition and characteristics of the two benchmarks used in the paper.
read the caption
Table 1: Overview of our Lifelong Benchmarks. We list the constituent source datasets (deduplicated) and their statistics for constructing our lifelong benchmarks here. Our benchmarks encompass a wide-range of natural and synthetic domains, sources and distribution shifts, making for a comprehensive lifelong testbed.
In-depth insights#
Lifelong Benchmarking#
Lifelong benchmarking presents a paradigm shift in evaluating machine learning models. Traditional static benchmarks, while useful initially, suffer from overfitting as models become specialized to their quirks. Lifelong benchmarks, in contrast, dynamically expand with new data and models, mitigating this issue and ensuring ongoing relevance. This approach, however, introduces challenges: the high computational cost of evaluating numerous models on massive datasets. The paper’s innovation lies in addressing this challenge through efficient evaluation techniques, such as Sort & Search, which leverage dynamic programming and sample selection to drastically reduce the computational burden. This enables researchers to continuously monitor model performance and ensure that benchmarks remain representative of the ever-evolving capabilities of machine learning models, maintaining a more reliable and unbiased evaluation process. The efficacy of this method in reducing evaluation costs by up to 1000x is a significant advancement in evaluating large-scale model collections.
Sort & Search#
The proposed method, “Sort & Search,” presents a novel approach to efficient lifelong model evaluation by cleverly combining two key operations. The ‘Sort’ component efficiently ranks test samples based on their difficulty, leveraging previously computed results to drastically reduce the computational cost. This ranking is achieved through a dynamic programming approach that determines the difficulty using the overall accuracy across all previous models. The ‘Search’ component then strategically selects a subset of the ranked samples for evaluating new models. This selection process is optimized to minimize evaluation cost while maximizing accuracy prediction, significantly improving the efficiency compared to traditional methods that evaluate all samples for every new model. The synergy between ‘Sort’ and ‘Search’ is crucial to the success of the approach, as the sample ranking informs the efficient selection process, enabling sub-linear evaluation cost with minimal loss in accuracy. The paper showcases the effectiveness of Sort & Search through empirical evidence, demonstrating significant improvements in computational speed and accuracy when compared to baseline methods. Further research is suggested to investigate generalizing the ranking algorithm beyond a single, global ordering to further improve efficiency and to adapt the method for different task types.
Sample-wise Metrics#
The concept of sample-wise metrics in model evaluation offers a nuanced perspective compared to aggregate metrics. Instead of focusing solely on overall accuracy, sample-wise metrics delve into the model’s performance on individual data points. This granular analysis reveals valuable insights into a model’s strengths and weaknesses across different data characteristics. For instance, it can pinpoint whether a model struggles with specific types of images or text, or if its errors are systematically biased towards certain classes. This detailed understanding is crucial for identifying and mitigating biases, improving model robustness, and facilitating a more comprehensive understanding of model behavior. Sample-wise metrics also enable advanced analysis techniques, allowing researchers to correlate prediction errors with various data attributes. Such analyses could reveal unexpected relationships between the model’s performance and specific data properties, potentially highlighting previously unknown limitations or suggesting modifications to data collection strategies. The benefits of sample-wise analysis extend beyond research, proving useful for debugging and enhancing model reliability in real-world applications.
Error Decomposition#
Error decomposition in machine learning model evaluation is crucial for understanding the sources of prediction inaccuracies. By breaking down the total error into its constituent parts, researchers can gain valuable insights into the strengths and weaknesses of their models and the underlying data. In the context of lifelong learning, where models are continuously updated with new data, error decomposition can highlight how the addition of new data impacts various error components. For instance, it might reveal if new data primarily increases aleatoric uncertainty (inherent randomness in the data) or epistemic uncertainty (uncertainty due to limited knowledge). Identifying the dominant type of error is key for guiding model improvement strategies. If epistemic uncertainty is high, efforts should focus on improving model architecture or training procedures to capture more knowledge. Conversely, if aleatoric error is dominant, the focus should shift to data quality and collection techniques. Analyzing the interplay between different error components over time can reveal important trends, revealing how model performance evolves as the dataset expands, and pointing to potential bottlenecks in the model or data. Ultimately, effective error decomposition enhances the evaluation of machine learning models, particularly in lifelong learning scenarios, by providing a fine-grained view of model performance and suggesting targeted strategies for enhancement.
Future Directions#
Future research should prioritize extending the Sort & Search framework beyond single-rank ordering. The current method’s reliance on a single ranking of sample difficulty limits its generalizability. Exploring alternative ranking strategies or clustering techniques to categorize samples by difficulty, rather than a single global order, is crucial. This would allow the method to better adapt to varied model behaviors and diverse difficulty distributions. Investigating how to efficiently identify and incorporate “harder” samples, improving its capacity for lifelong learning, would greatly enhance its capabilities. Furthermore, research should focus on applying the Sort & Search framework to foundation models and other domains, enabling a broader evaluation of more complex models. Addressing the inherent limitations in existing overall accuracy prediction metrics by developing more sample-level based metrics is also needed. This shift toward finer-grained analysis is crucial for a more nuanced understanding of model performance. Finally, a deeper exploration of the relationship between model performance across different task types is important for enhancing the framework’s suitability for various applications.
More visual insights#
More on figures
🔼 This figure illustrates the core idea of the Sort & Search method proposed in the paper. The left side shows the initial state with n samples and m models already evaluated. The right side demonstrates how to efficiently evaluate a new model (top) and add a new sample (bottom) without evaluating all models on all samples. The new model evaluation leverages a subset of samples selected based on difficulty (determined using existing model evaluations), reducing computation cost. Similarly, the new sample insertion identifies its difficulty using a subset of models. The overall goal is to maintain efficient evaluation of an ever-growing benchmark.
read the caption
Figure 1: Efficient Lifelong Model Evaluation. Assume an initial pool of n samples and m models evaluated on these samples (left). Our goal is to efficiently evaluate a new model (insertM) at sub-linear cost (right top) and efficiently insert a new sample into the lifelong benchmark (insertD) by determining sample difficulty at sub-linear cost (right bottom). See Section 2 for more details.
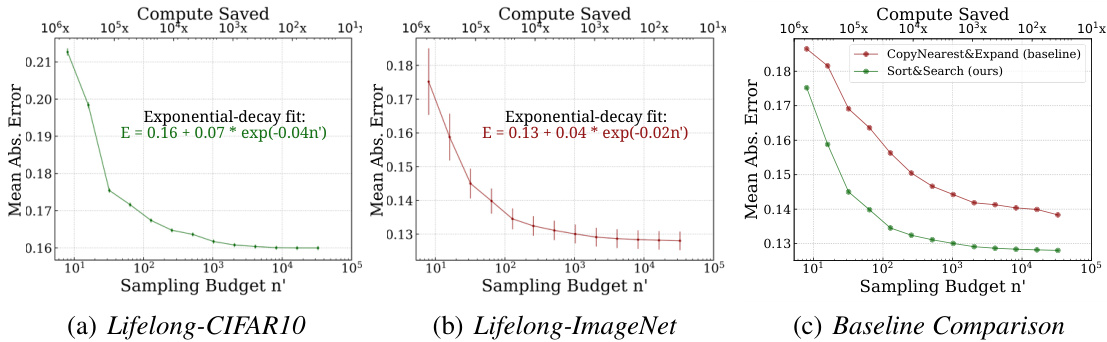
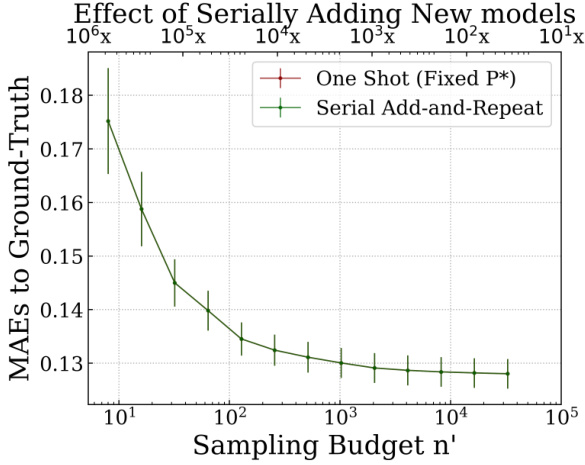
🔼 This figure presents the main results of the Sort & Search method. Subfigures (a) and (b) show the significant reduction in computation cost (99%) achieved by Sort & Search for evaluating new models on the Lifelong-CIFAR10 and Lifelong-ImageNet benchmarks respectively. The mean absolute error (MAE) decreases exponentially as the sampling budget (n’) increases, demonstrating the efficiency of the method. Subfigure (c) provides a comparison of Sort & Search against a baseline method, highlighting its superior efficiency and accuracy.
read the caption
Figure 3: Main Results. (a,b) We achieve 99% cost-savings for new model evaluation on Lifelong-ImageNet and Lifelong-CIFAR10 showcasing the efficiency (MAE decays exponentially with n') of Sort&Search. (c) S&S is more efficient and accurate compared to the baseline on Lifelong-ImageNet.

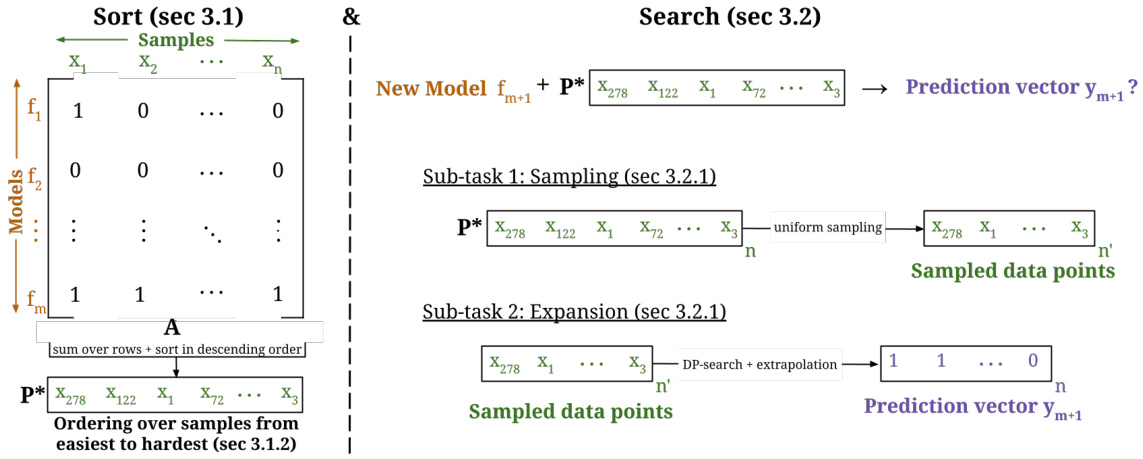
🔼 This figure illustrates the overall process of the Sort & Search framework. The left side shows the sorting of samples based on their difficulty, which is determined by the initial evaluation results. The right side depicts the sampling process and the subsequent prediction of a new model’s performance on the remaining samples using dynamic programming. The figure also highlights how the framework can be applied to efficiently insert new samples into the existing benchmark.
read the caption
Figure 2: Full Pipeline of Sort & Search. For efficiently evaluating new models, (Left) we first sort all data samples by difficulty (refer Section 3.1) and (Right) then perform a uniform sampling followed by DP-search and extrapolation for yielding new model predictions (refer Section 3.2). This entire framework can also be transposed to efficiently insert new samples (refer Section 3.3).
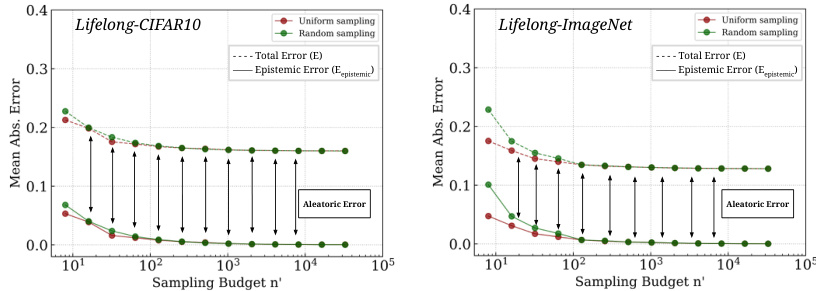
🔼 The figure shows the error decomposition analysis on two lifelong benchmark datasets: Lifelong-CIFAR10 and Lifelong-ImageNet. It demonstrates that the epistemic error (the error that can be reduced by increasing the sampling budget) quickly diminishes to near zero, while the aleatoric error (irreducible error due to model misalignment with the sample ranking) remains the dominant source of error. This finding suggests that improving the model’s ability to generalize beyond a single ranking, rather than focusing solely on better sampling, may be crucial for enhancing future model evaluation efficiency.
read the caption
Figure 5: Error Decomposition Analysis on Lifelong-CIFAR10 (left) and Lifelong-ImageNet (right). We observe that epistemic error (solid line) drops to 0 within only 100 to 1000 samples across both datasets, indicating this error cannot be reduced further by better sampling methods. The total error E is almost entirely irreducible (Aleatoric), induced because new models do not perfectly align with the ranking order P*. This suggests generalizing beyond a single rank ordering, not better sampling strategies, should be the focus of subsequent research efforts.
🔼 This figure illustrates the core idea of the Sort & Search method for efficient lifelong model evaluation. The left side shows the initial state with ’n’ samples and ’m’ models already evaluated. The right side demonstrates how to efficiently add a new model (top) and a new sample (bottom) to the existing benchmark. The efficiency is achieved by using dynamic programming to selectively evaluate only a subset of samples and models, rather than evaluating everything.
read the caption
Figure 1: Efficient Lifelong Model Evaluation. Assume an initial pool of n samples and m models evaluated on these samples (left). Our goal is to efficiently evaluate a new model (insertM) at sub-linear cost (right top) and efficiently insert a new sample into the lifelong benchmark (insertD) by determining sample difficulty at sub-linear cost (right bottom). See Section 2 for more details.

🔼 This figure illustrates the core idea of the Sort & Search method for efficient lifelong model evaluation. The left side shows the initial state with n samples and m models already evaluated. The right side demonstrates how to efficiently evaluate a new model (top) and add a new sample (bottom) using Sort & Search. Efficient evaluation is achieved by leveraging dynamic programming to selectively choose subsets of samples and models, thus avoiding the need for complete re-evaluation with each addition.
read the caption
Figure 1: Efficient Lifelong Model Evaluation. Assume an initial pool of n samples and m models evaluated on these samples (left). Our goal is to efficiently evaluate a new model (insertM) at sub-linear cost (right top) and efficiently insert a new sample into the lifelong benchmark (insertD) by determining sample difficulty at sub-linear cost (right bottom). See Section 2 for more details.
🔼 This figure illustrates the core concept of efficient lifelong model evaluation. The left side shows the initial state with ’n’ samples and ’m’ models already evaluated. The right side demonstrates the two key goals: efficiently evaluating a new model (top) without evaluating it on all samples and efficiently inserting a new sample (bottom) by determining its difficulty. The figure uses a matrix representation to show the model evaluations and highlights the sub-selection process for both models and samples to achieve efficiency.
read the caption
Figure 1: Efficient Lifelong Model Evaluation. Assume an initial pool of n samples and m models evaluated on these samples (left). Our goal is to efficiently evaluate a new model (insertM) at sub-linear cost (right top) and efficiently insert a new sample into the lifelong benchmark (insertD) by determining sample difficulty at sub-linear cost (right bottom). See Section 2 for more details.
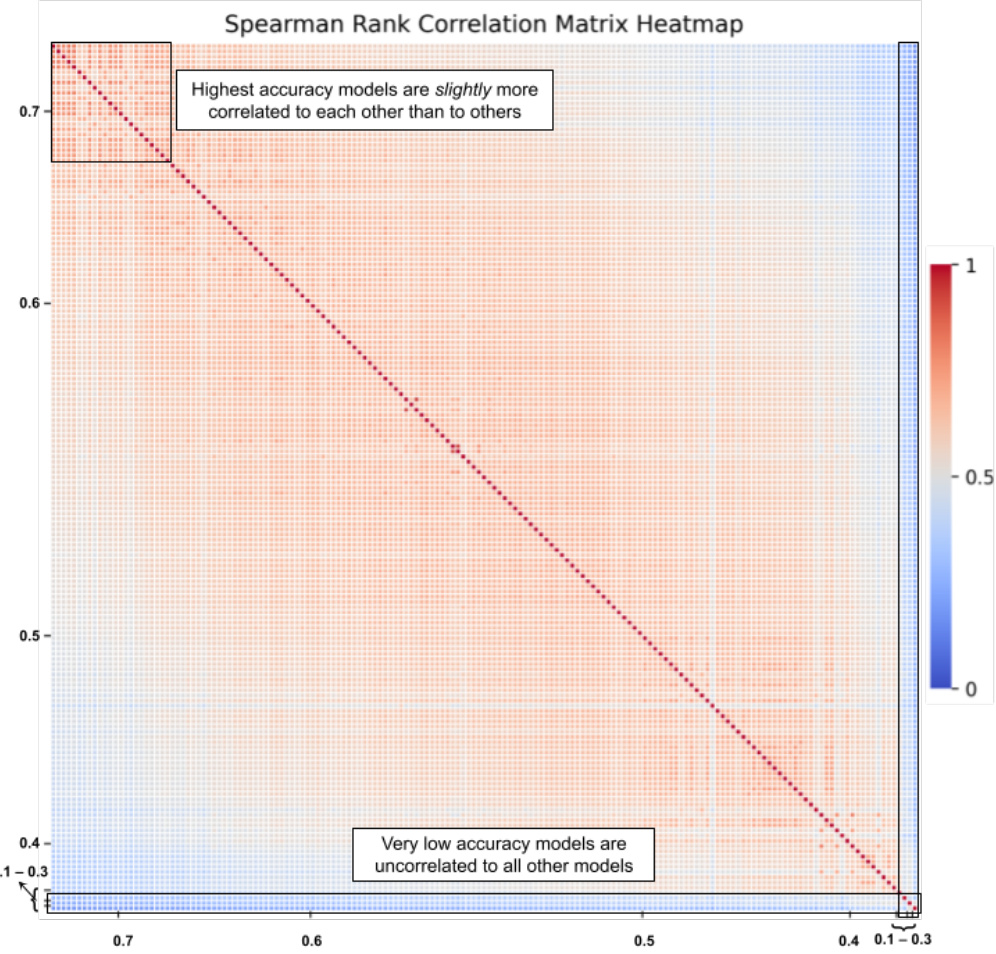
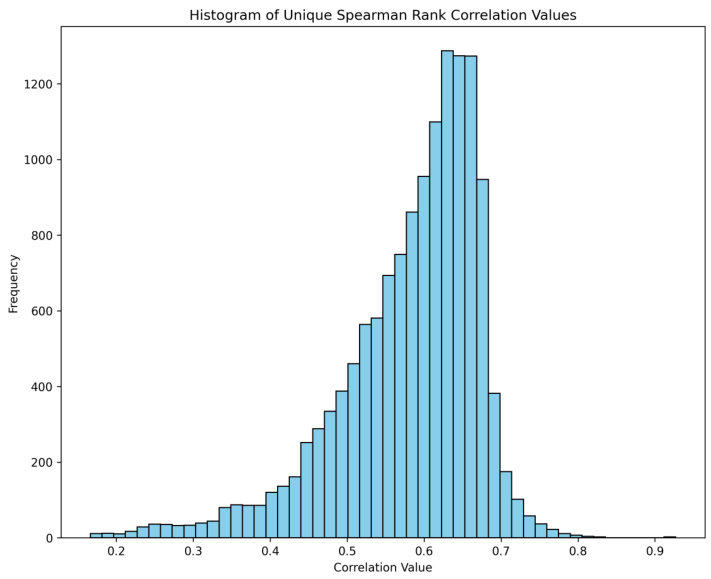
🔼 This figure shows the results of a correlation analysis performed on the predictions of 167 models on the Lifelong-ImageNet dataset. Panel (a) demonstrates that all Spearman rank correlations between model predictions are positive, highlighting a general similarity in model behavior despite their architectural differences. Panel (b) visualizes a heatmap of the correlation matrix, where models are ordered by their accuracy. Higher accuracy models show slightly higher correlations with each other compared to lower accuracy models, and very low accuracy models have almost no correlation with other models.
read the caption
Figure 7: Correlation Analysis between Model Predictions on Lifelong-ImageNet. (a) We note that all correlations between model predictions are positive, signifying the similarities between all models despite their diverse sizes, architectures, and inductive biases. (b) We show the cross-correlation matrix between all model predictions—the x and y axes showcase models, sorted by their accuracies. The floating point numbers on the x and y axes are the model accuracies—the highest accuracy models (70% accuracy) appear at the top and left, while the lowest accuracy models appear at the bottom and right (10% - 30%).
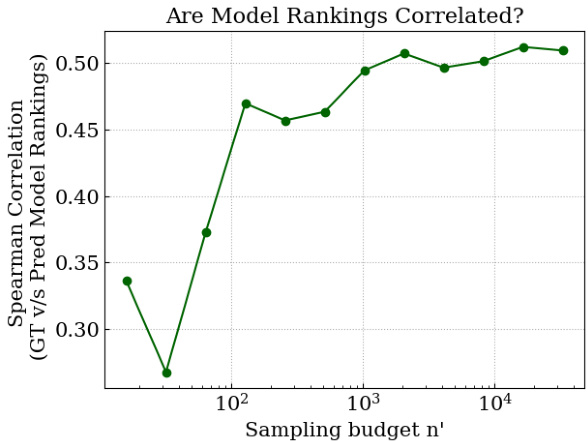
🔼 This figure shows the Spearman correlation between the ground truth model rankings and the model rankings predicted by Sort & Search for different sampling budgets. High correlations (above 0.5) indicate that Sort & Search maintains the relative ordering of models even with a small sample size, demonstrating its effectiveness in practical applications where model ranking is important.
read the caption
Figure 8: We change the metric for evaluating the efficacy of Sort & Search from MAE to Spearman correlation-we observe consistently high correlations of 0.5 or greater.
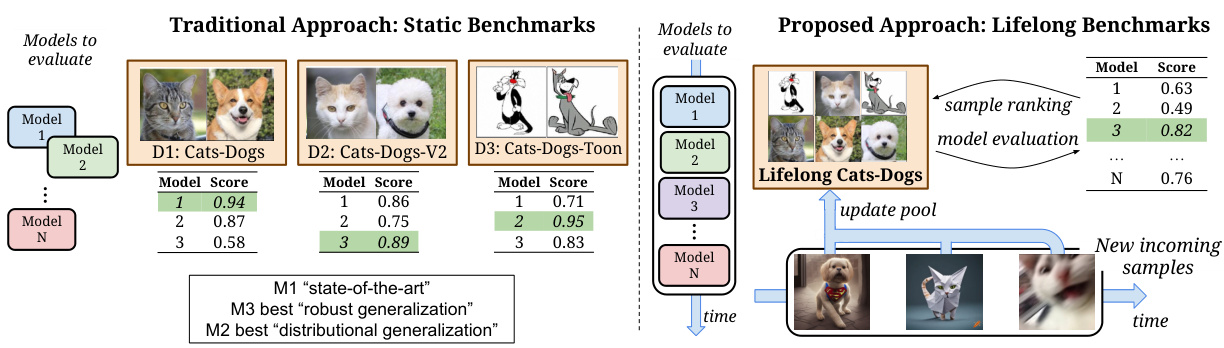
🔼 This figure compares traditional static benchmarks with the proposed lifelong benchmarks. Static benchmarks focus on fixed datasets, leading to overfitting and limited generalizability. In contrast, lifelong benchmarks use continuously expanding datasets, promoting better generalization and mitigating overfitting.
read the caption
Figure 6: Static vs Lifelong Benchmarking. (Top) Static benchmarks incentivise machine learning practitioners to overfit models to specific datasets, weakening their ability to assess generalisation. (Bottom) We conceptualise Lifelong Benchmarks as an alternative paradigm—ever-expanding pools of test samples that resist overfitting while retaining computational tractability.
Full paper#



















