On the Sparsity of the Strong Lottery Ticket Hypothesis

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it provides the first rigorous proof of the Strong Lottery Ticket Hypothesis (SLTH) with guarantees on subnetwork sparsity. This addresses a major limitation of previous SLTH research and opens exciting avenues for creating more efficient and resource-friendly neural networks.

Visual Insights

#

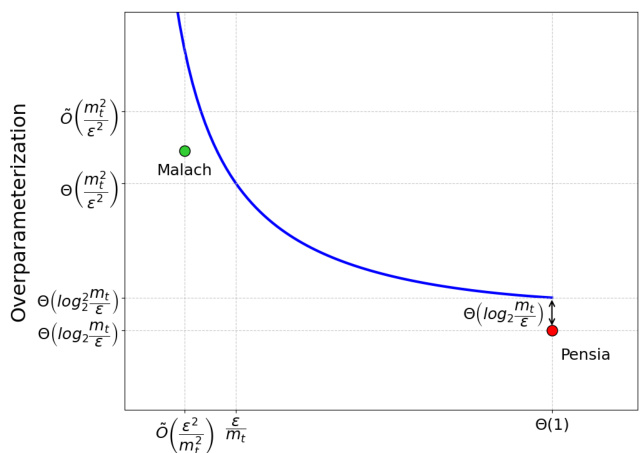
This figure shows the relationship between the density (γ) of a winning ticket and the overparameterization required to achieve a certain level of approximation error (ε). The x-axis represents the density of the winning ticket (ranging from very sparse to dense), and the y-axis represents the overparameterization (m/mt, where m is the number of parameters in the random network and mt is the number of parameters in the target network). The blue curve represents the overparameterization needed according to Theorem 3 of the paper, showing a decrease in overparameterization as density increases. Points for previous results by Malach et al. and Pensia et al. are also plotted for comparison.

In-depth insights

#

Sparse SLTH Proof

#

The hypothetical Sparse Strong Lottery Ticket Hypothesis (SLTH) proof tackles the challenge of demonstrating that a randomly-initialized, overparameterized neural network contains a sparse subnetwork capable of achieving comparable performance to the full network, without any training. A key innovation would involve proving a tight bound on the Random Fixed-Size Subset Sum Problem (RFSS), a refinement of the original RSS problem used in previous SLTH proofs. This addresses the issue of previous proofs lacking guarantees on the size of the winning subnetwork, making the sparsity claim more meaningful. The approach likely involves showing that a sufficiently large random network can approximate any target network by selecting a subset of its weights, where the RFSS bound ensures the desired sparsity. Success would provide a deeper understanding of neural network generalization and potentially open avenues for developing efficient training algorithms for sparse neural networks, directly addressing the LTH’s original motivations. However, the complexity of such a proof necessitates rigorous mathematical arguments and a strong understanding of both probability theory and the structure of neural networks.

RFSS Problem

#

The Random Fixed-Size Subset Sum (RFSS) problem, a crucial component of the research, is a refined version of the Random Subset Sum (RSS) problem. Unlike RSS, which allows subsets of varying sizes, RFSS restricts subsets to a fixed size, making it a significantly more challenging problem to analyze. This constraint is particularly relevant to the Strong Lottery Ticket Hypothesis (SLTH), as it directly relates to finding sparse subnetworks of a fixed size within a larger network. The authors’ proof of an essentially tight bound for RFSS is a major contribution, offering a more precise understanding of the overparameterization required to guarantee the existence of these sparse subnetworks. This tight bound has substantial implications for the SLTH, allowing for a better analysis of the relationship between the size of the random network, the size of the target network, and the sparsity of the winning ticket. By focusing on fixed-size subsets, the RFSS provides a more practical framework for the SLTH. Furthermore, the RFSS’s tight bound is a valuable result for several related areas of theoretical computer science and mathematics.

Overparameterization

#

The concept of overparameterization in the context of the Strong Lottery Ticket Hypothesis (SLTH) is crucial. It explores the necessary excess of parameters in a randomly initialized neural network to guarantee the existence of a sparse subnetwork that accurately approximates a smaller target network. The paper investigates the relationship between this overparameterization and the sparsity (density) of the winning ticket, establishing a tight bound. Reducing overparameterization is beneficial for efficiency, thus the analysis provides insights into achieving optimal sparsity while minimizing the overall size of the initial network. The findings suggest a trade-off: higher sparsity requires greater overparameterization, highlighting the importance of balancing model size and accuracy. This work offers a refined understanding of the SLTH by quantifying the impact of sparsity on the required overparameterization, ultimately contributing to the development of more efficient and resource-conscious neural network training techniques.

SLTH Extensions

#

The Strong Lottery Ticket Hypothesis (SLTH) extensions explore the boundaries of its core principles. Initial work focused on dense networks, but extensions successfully broadened its applicability to convolutional and residual networks, demonstrating the pervasiveness of the phenomenon across various architectures. A significant advancement lies in proving SLTH for equivariant networks, which are increasingly important for handling structured data like images and graphs. Addressing the sparsity of winning tickets is crucial. While initial SLTH proofs didn’t guarantee sparsity, later research concentrated on tightly bounding the size of the pruned subnetworks, thereby enhancing practical relevance. Furthermore, investigations into the relationship between overparameterization and the desired sparsity level contribute to optimized network design and improved training strategies. The challenge of reliably finding these winning tickets remains an active area of investigation, with ongoing research exploring efficient algorithms to overcome this limitation. Ultimately, SLTH extensions aim at a deeper understanding of neural network training dynamics and architectures.

Future Work

#

The paper’s core contribution is a rigorous proof of the Strong Lottery Ticket Hypothesis (SLTH), focusing on sparsity guarantees. Future work could naturally explore several avenues. First, extending the Random Fixed-Size Subset Sum (RFSS) problem to a multidimensional version would significantly impact the analysis of structured pruning in convolutional neural networks (CNNs) and other structured architectures. This would enable a tighter analysis of overparameterization’s relationship with sparsity in more complex network topologies. Second, improving the efficiency of finding these sparse, high-performing subnetworks remains a crucial open problem. Algorithms surpassing simple pruning strategies are needed. Research into effective “training-by-pruning” techniques, possibly leveraging techniques from other areas of optimization, could be highly valuable. Finally, applying these theoretical results to real-world problems, and evaluating the practical implications of the findings in terms of computational cost and performance on diverse datasets, is essential for realizing the full potential of this work. Improved empirical validation across diverse tasks, alongside a thorough investigation of the practical implications for training and deploying models, would be beneficial.

More visual insights

#

More on figures

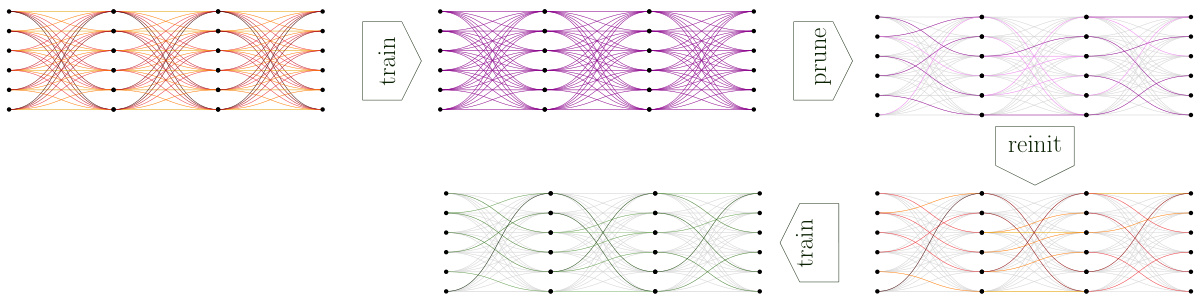
This figure illustrates the Lottery Ticket Hypothesis (LTH). It shows a large, fully-connected neural network. The network is iteratively pruned, where the weights with the smallest absolute values are removed and the remaining weights are reset to their initial values. This process is repeated until a sparse subnetwork is obtained. The key finding is that this sparse network achieves comparable or better performance than the original network.

This figure illustrates the Lottery Ticket Hypothesis (LTH). It shows a process where a large, randomly initialized neural network is iteratively pruned. The pruning involves removing weights with small magnitudes and resetting the remaining weights to their initial values. The key observation is that even after significant pruning, the resulting smaller network can still achieve comparable performance to the original larger network, demonstrating the existence of ‘winning tickets’ within larger networks.

Full paper

#