↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Bayesian neural networks (BNNs) are increasingly used, but their high dimensionality necessitates efficient inference methods like Hamiltonian Monte Carlo (HMC). However, the non-differentiability of activation functions like ReLU poses challenges for HMC. Classical HMC analysis assumes smooth energy functions, leading to inaccurate error rate estimations and inefficient sampling when applied to ReLU networks. This paper addresses these issues by analyzing HMC’s error rates in non-smooth settings and proposing solutions.
The researchers show that HMC for ReLU networks exhibits a much higher local error rate (Ω(ε)) than the classical rate (O(ε³)), causing a high rejection rate. This inefficiency is verified through both theoretical analysis and experiments on synthetic and real-world data. Importantly, they offer new guidelines for tuning HMC with non-differentiable components, suggesting an optimal acceptance probability of 0.45 and a step size scaling of d⁻¹/². This work highlights the limitations of relying on classical HMC guidelines for ReLU networks and provides valuable insights for researchers working on Bayesian deep learning.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers employing Hamiltonian Monte Carlo (HMC) for Bayesian neural network inference, especially those using ReLU activation functions. It reveals the inefficiency of HMC with ReLU networks due to high rejection rates, impacting the reliability and scalability of Bayesian deep learning. The findings necessitate a re-evaluation of HMC’s applicability and encourage exploration of alternative sampling methods, influencing both theoretical understanding and practical applications of Bayesian neural networks. The proposed optimal scaling guideline for HMC with non-differentiable log-densities provides a new avenue for tuning HMC, enhancing the method’s efficiency in a broader range of scenarios.
Visual Insights#
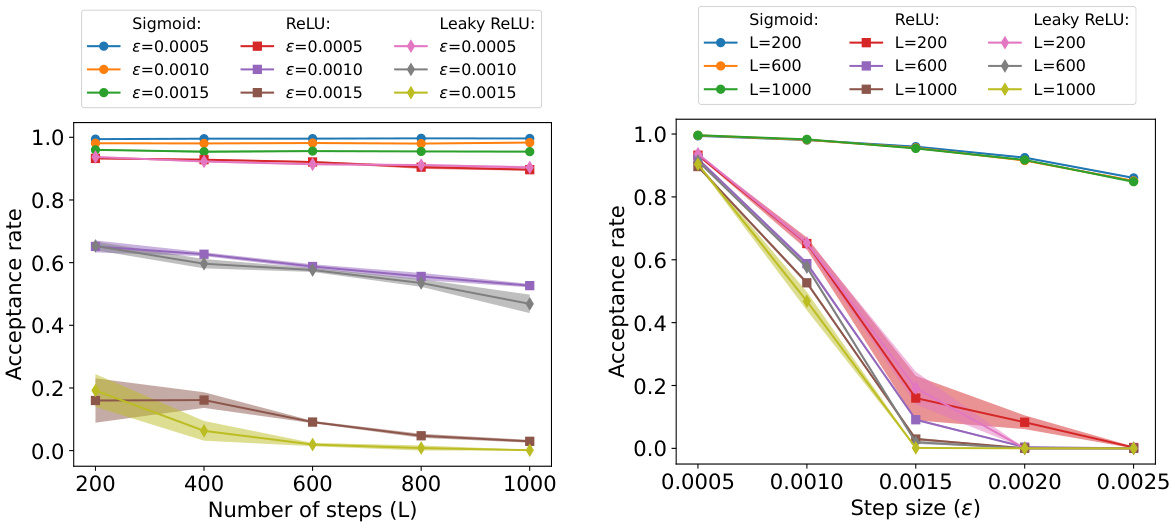
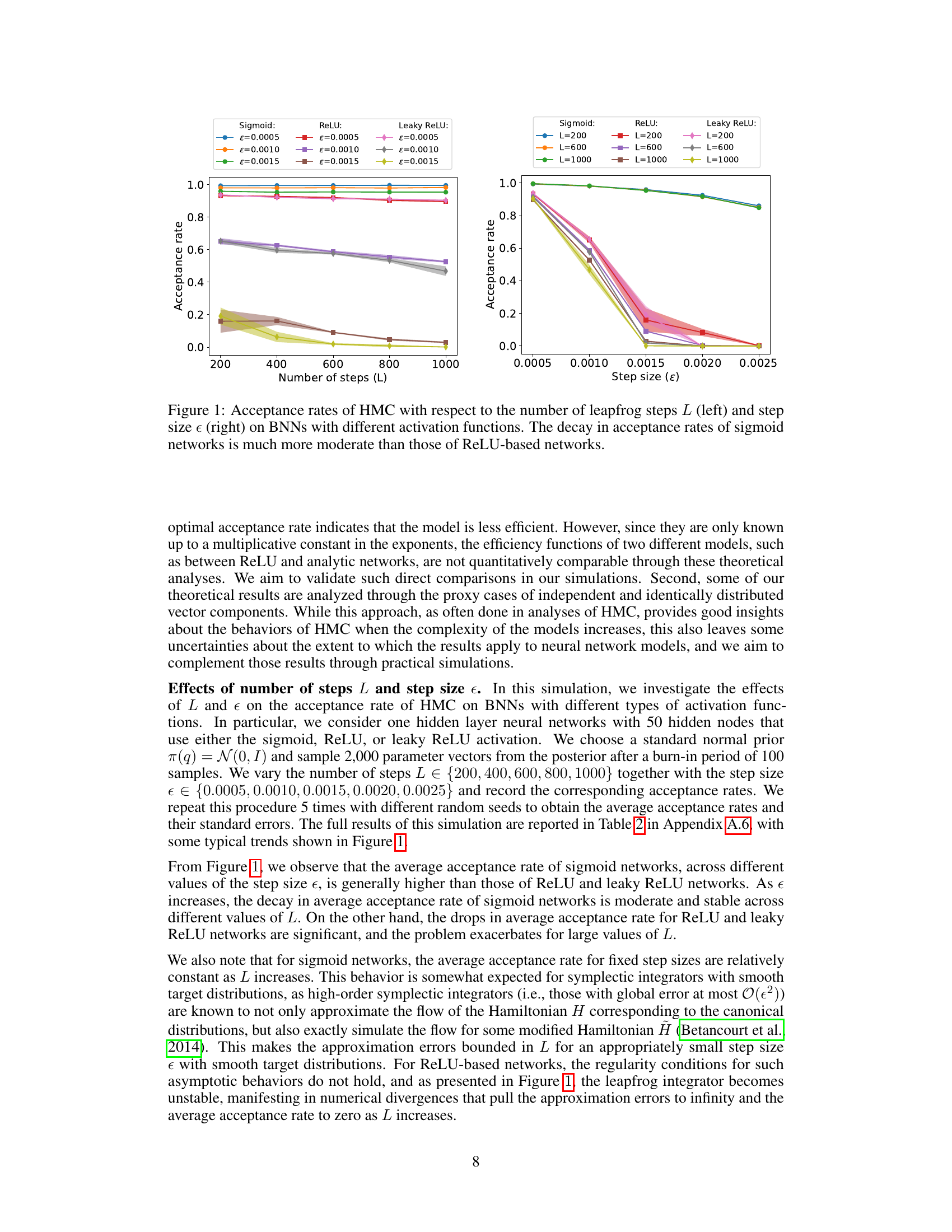
This figure shows the results of a simulation to investigate the effects of the number of steps L and step size ε on the acceptance rate of the Hamiltonian Monte Carlo (HMC) algorithm for Bayesian neural networks (BNNs) with different activation functions (sigmoid, ReLU, and leaky ReLU). The left panel shows the acceptance rate as a function of the number of steps L for different values of ε, while the right panel shows the acceptance rate as a function of ε for different values of L. The results show that the acceptance rate of sigmoid networks is much more stable and less sensitive to changes in L and ε compared to ReLU-based networks.
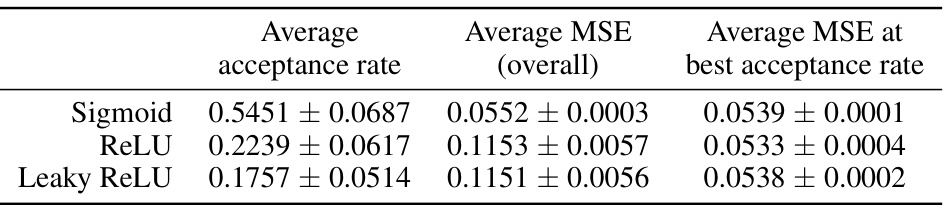
This table presents the results of experiments on the UTKFace dataset using three different activation functions (Sigmoid, ReLU, and Leaky ReLU). It compares the average acceptance rate, the overall average Mean Squared Error (MSE), and the MSE achieved at the best acceptance rate for each activation function. The results show that the Sigmoid activation function leads to a better average acceptance rate and lower overall MSE compared to ReLU and Leaky ReLU. However, when comparing MSE at their best acceptance rate, there is little difference among the three activation functions.
In-depth insights#
ReLU HMC Shortcomings#
The heading ‘ReLU HMC Shortcomings’ aptly encapsulates the core findings of the research. The paper likely demonstrates that the Hamiltonian Monte Carlo (HMC) algorithm, while effective for Bayesian inference with neural networks possessing smooth activation functions, suffers from significant inefficiencies when applied to networks using Rectified Linear Units (ReLUs). The non-differentiability of ReLU at zero introduces a large local error rate in the leapfrog integrator used within HMC, resulting in a much higher rejection rate for proposed samples. This inefficiency stems from the algorithm’s inability to smoothly navigate the non-differentiable points in the energy landscape, leading to frequent proposal rejections and slower convergence. The paper likely supports these claims with theoretical analysis showing the increased error rate, and empirical evidence demonstrating significantly lower acceptance rates and efficiency for ReLU networks compared to smoother alternatives like sigmoid functions. The key insight is the contrast between the classical O(ε³) error rate for smooth functions and the demonstrated Ω(ε) rate for ReLU, highlighting a fundamental limitation of HMC in this specific context. This highlights the need for alternative sampling methods or modified algorithms specifically designed to handle the non-differentiability of ReLU-based neural networks more effectively.
Leapfrog Error Analysis#
A leapfrog integrator’s error analysis within the context of Hamiltonian Monte Carlo (HMC) applied to ReLU neural networks is crucial because it directly impacts the algorithm’s efficiency and accuracy. Standard HMC error analysis assumes smooth energy functions, which is violated by the non-differentiability of ReLU activation functions. Therefore, a rigorous analysis must account for the discontinuities in the gradients. The core of such an analysis involves examining the local error incurred when a leapfrog step crosses a region of non-differentiability. This would reveal that instead of the typical O(ε³) error rate for smooth functions, a significantly larger Ω(ε) rate emerges, drastically affecting the acceptance probability and rendering HMC on ReLU networks inefficient for high-dimensional problems. The theoretical findings regarding this increased error rate should be confirmed and contextualized via empirical simulations, showing the impact of the step size, number of steps, and model dimensionality on both the acceptance rate and overall efficiency. Analyzing the optimal tuning of the HMC parameters in this non-smooth context also requires investigation. The contrast between the observed behavior in ReLU networks and that of smooth activation functions like sigmoids will emphasize the importance of this specialized error analysis.
Optimal HMC Tuning#
Optimal HMC tuning focuses on finding the best balance between computational cost and the acceptance rate. Step size (ε) and number of leapfrog steps (L) are crucial parameters. Smaller step sizes reduce error but increase computation, while larger steps risk inaccurate sampling. Optimal acceptance rates, often around 65%, are targeted to balance exploration and acceptance. However, the optimal tuning strategies significantly depend on the characteristics of the target distribution, which can change dramatically, depending on if the target distribution is smooth or non-differentiable. For instance, with ReLU networks, the non-differentiability introduces significant challenges, leading to an optimal acceptance rate closer to 45% and a different scaling of step size with dimensionality compared to smooth distributions. This highlights the importance of considering the specific properties of the problem when tuning HMC.
Synthetic Data Tests#
In a research paper’s ‘Synthetic Data Tests’ section, one would expect a thorough evaluation of the proposed method using artificially generated datasets. This approach allows for precise control over data characteristics, enabling a focused investigation of algorithm performance under various conditions. Key aspects of these tests might include assessing the model’s accuracy, efficiency, and robustness across different data distributions and noise levels. The choice of synthetic data generation methods is crucial, requiring justification and discussion of its suitability for evaluating specific algorithm properties. Detailed analysis would include statistical measures (e.g., mean squared error, precision/recall) as well as visualizations demonstrating the model’s behavior in various scenarios. Results from synthetic tests offer valuable insights into the strengths and weaknesses of the algorithm, providing a controlled baseline before moving to real-world data. It is important to assess whether performance on synthetic data translates to real-world applications, highlighting the importance of using realistic synthetic datasets that mimic relevant aspects of the target problem. Comparison with existing methods using the same synthetic data is a standard way to showcase the proposed algorithm’s relative merits.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending the theoretical analysis to other activation functions beyond ReLU, such as variations of ReLU or other piecewise-linear functions, would provide a more comprehensive understanding of HMC’s efficiency in non-smooth settings. Further investigation into the relationship between network architecture (depth, width, and connectivity) and the number of non-differentiability crossings is crucial for refining HMC tuning guidelines. Developing algorithmic modifications or alternative sampling methods to mitigate the inefficiency of HMC with non-smooth energy functions is also a key area of future work. This might include investigating surrogate functions, adaptive step size strategies, or alternative integrators better suited to non-differentiable landscapes. Finally, empirical validation on a wider range of real-world datasets and complex neural network models will be important to confirm the generalizability of the findings and to provide more practical guidance for Bayesian deep learning.
More visual insights#
More on figures
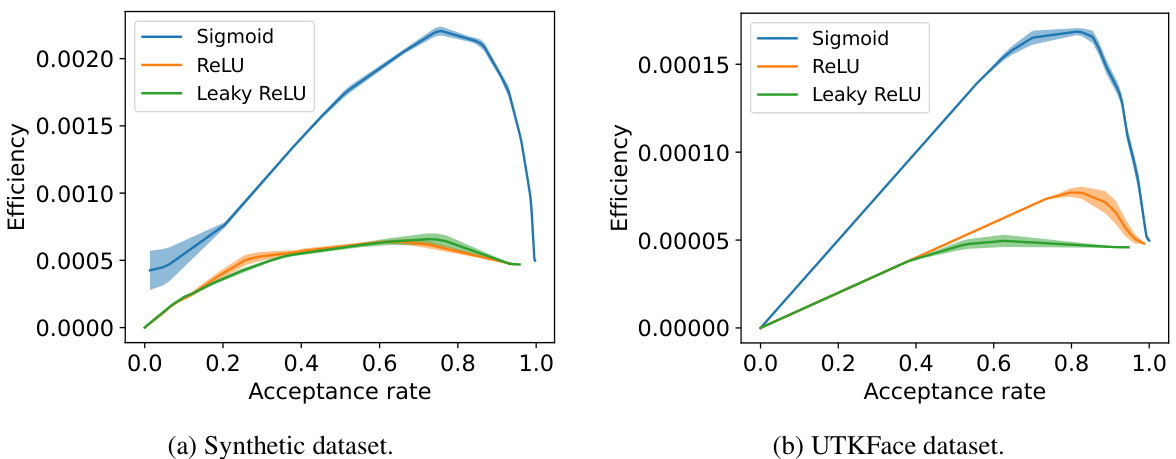
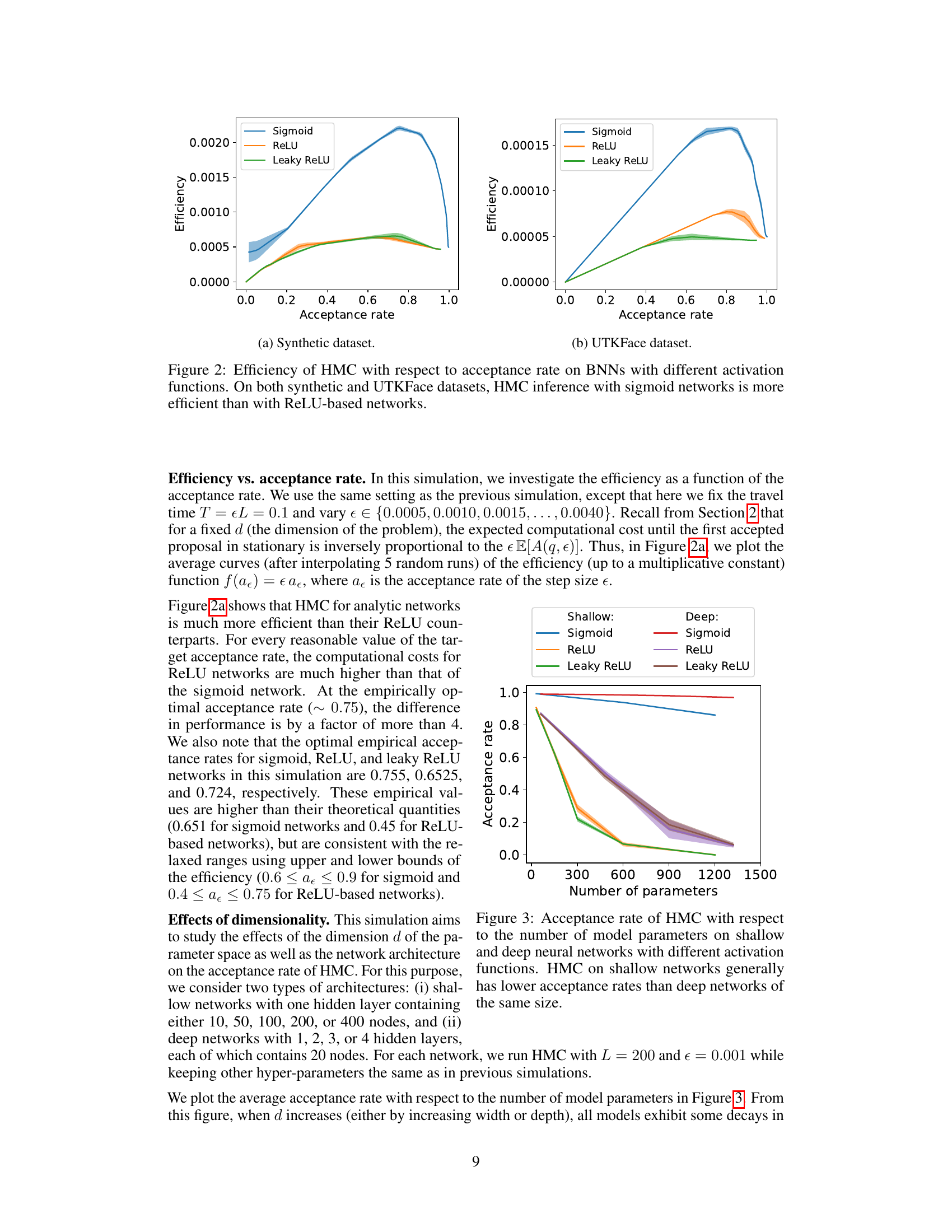
This figure compares the efficiency of Hamiltonian Monte Carlo (HMC) using sigmoid and ReLU activation functions across different acceptance rates. The efficiency is measured by considering both the acceptance rate and computational cost. Two datasets are used for the evaluation: a synthetic dataset and the UTKFace dataset. The results consistently show that HMC with sigmoid activation is far more efficient than that with ReLU activation for both datasets.
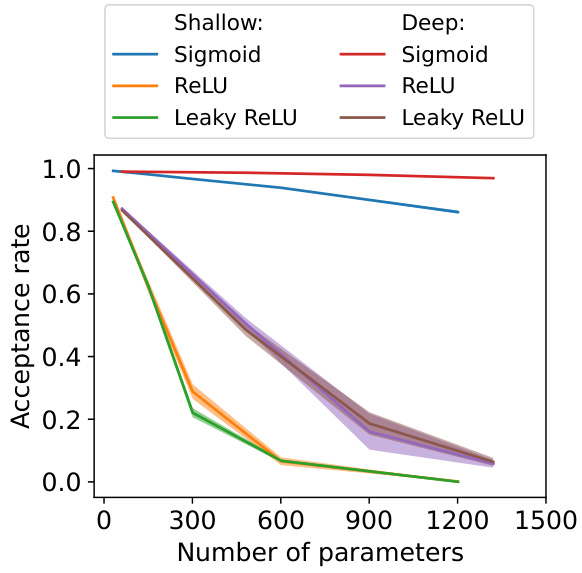
This figure shows how the acceptance rate of the Hamiltonian Monte Carlo (HMC) algorithm changes with the number of parameters in the model, for both shallow and deep neural networks. Three different activation functions (Sigmoid, ReLU, Leaky ReLU) are compared. The key observation is that shallower networks tend to have lower acceptance rates than deeper networks with the same number of parameters. The acceptance rate decreases significantly as the number of parameters increases, particularly for ReLU and Leaky ReLU activation functions.
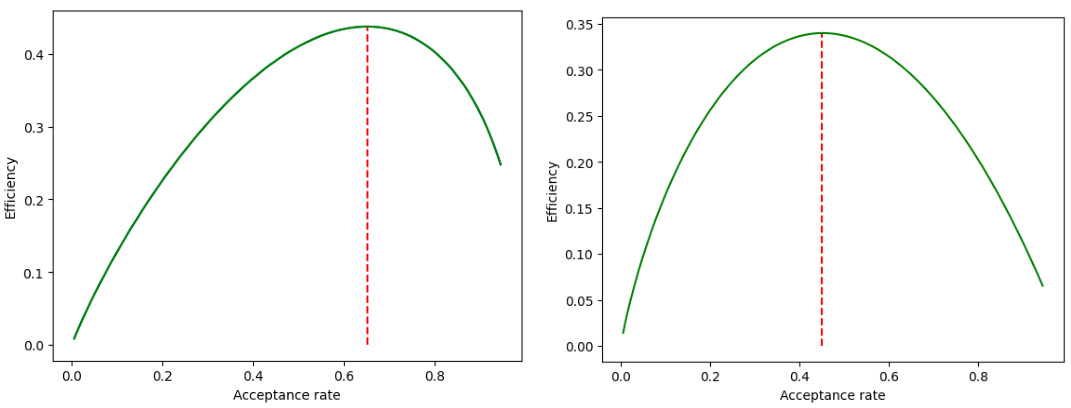
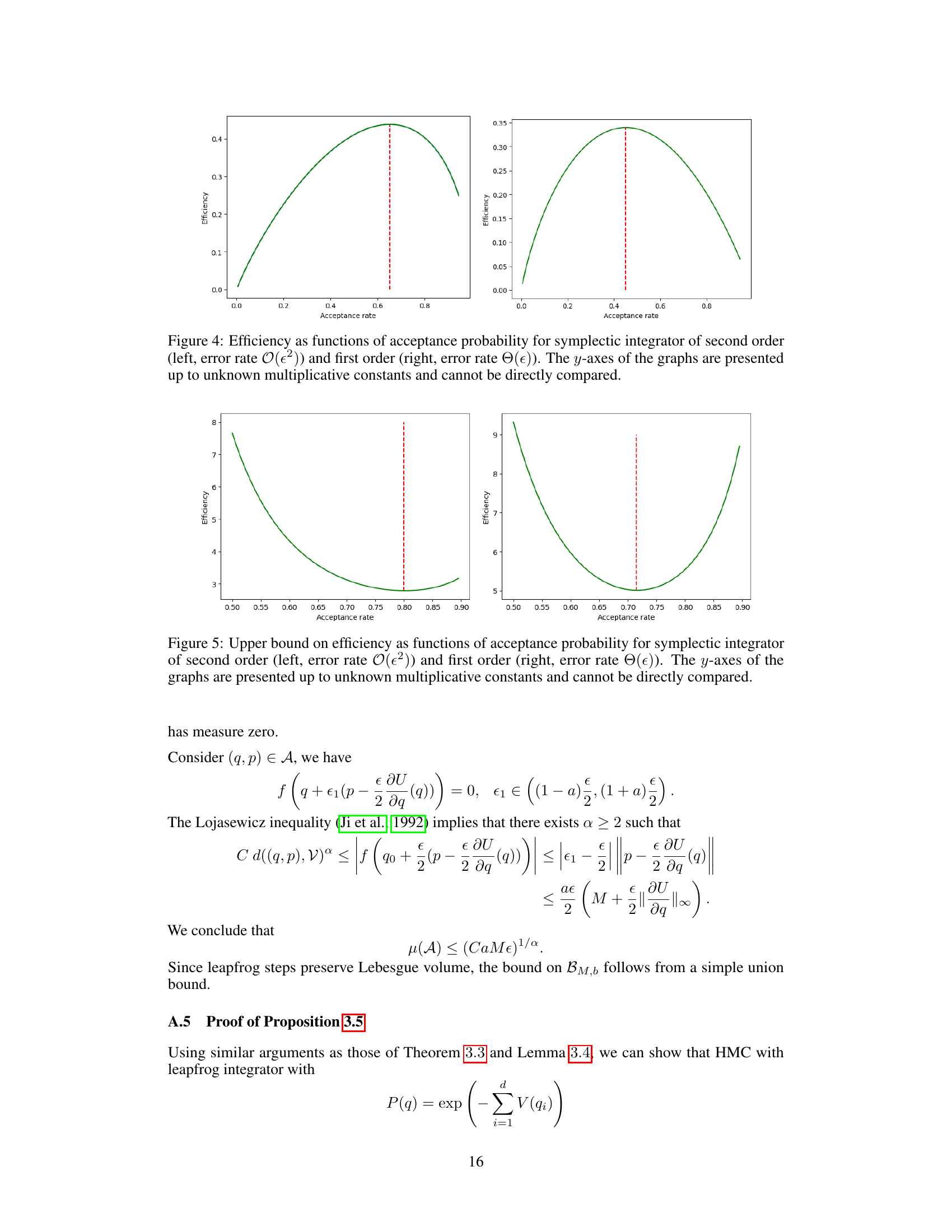
This figure shows the efficiency of symplectic integrators as a function of their acceptance probability. The left panel shows the results for a second-order integrator (error rate proportional to ε²), while the right panel shows results for a first-order integrator (error rate proportional to ε). The y-axis represents efficiency, and the x-axis is the acceptance rate. The vertical dashed lines mark the optimal acceptance rates. Importantly, the y-axes are scaled arbitrarily, so direct comparison between the two plots is not possible; the key takeaway is the difference in the shapes of the curves and the location of the optimal acceptance rate.
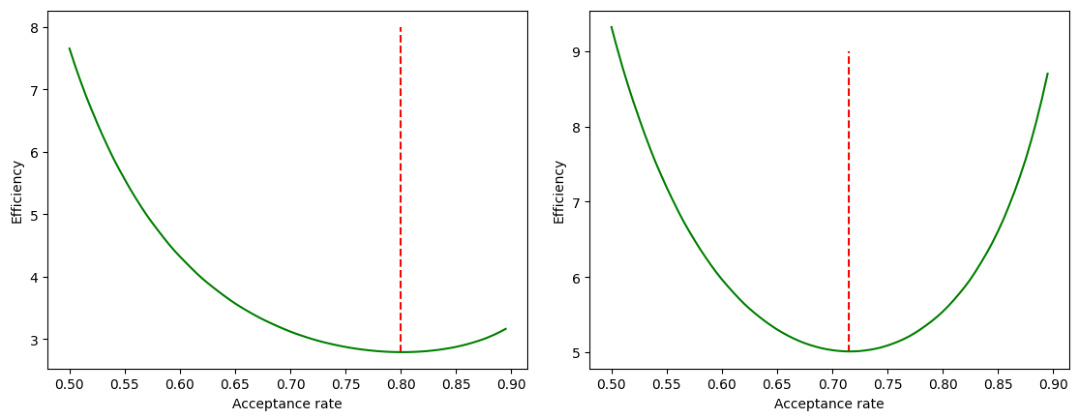
This figure shows the efficiency of symplectic integrators of the second order (left) and the first order (right) as a function of the acceptance probability. The y-axis represents efficiency, and the x-axis represents the acceptance probability. The graphs are shown up to unknown multiplicative constants, and cannot be directly compared. The red dotted lines in both graphs indicate the optimal acceptance probabilities.
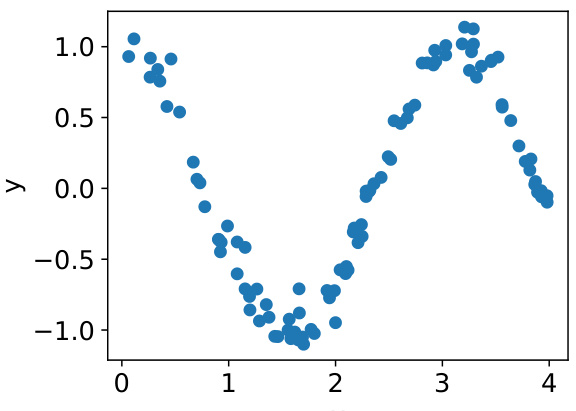
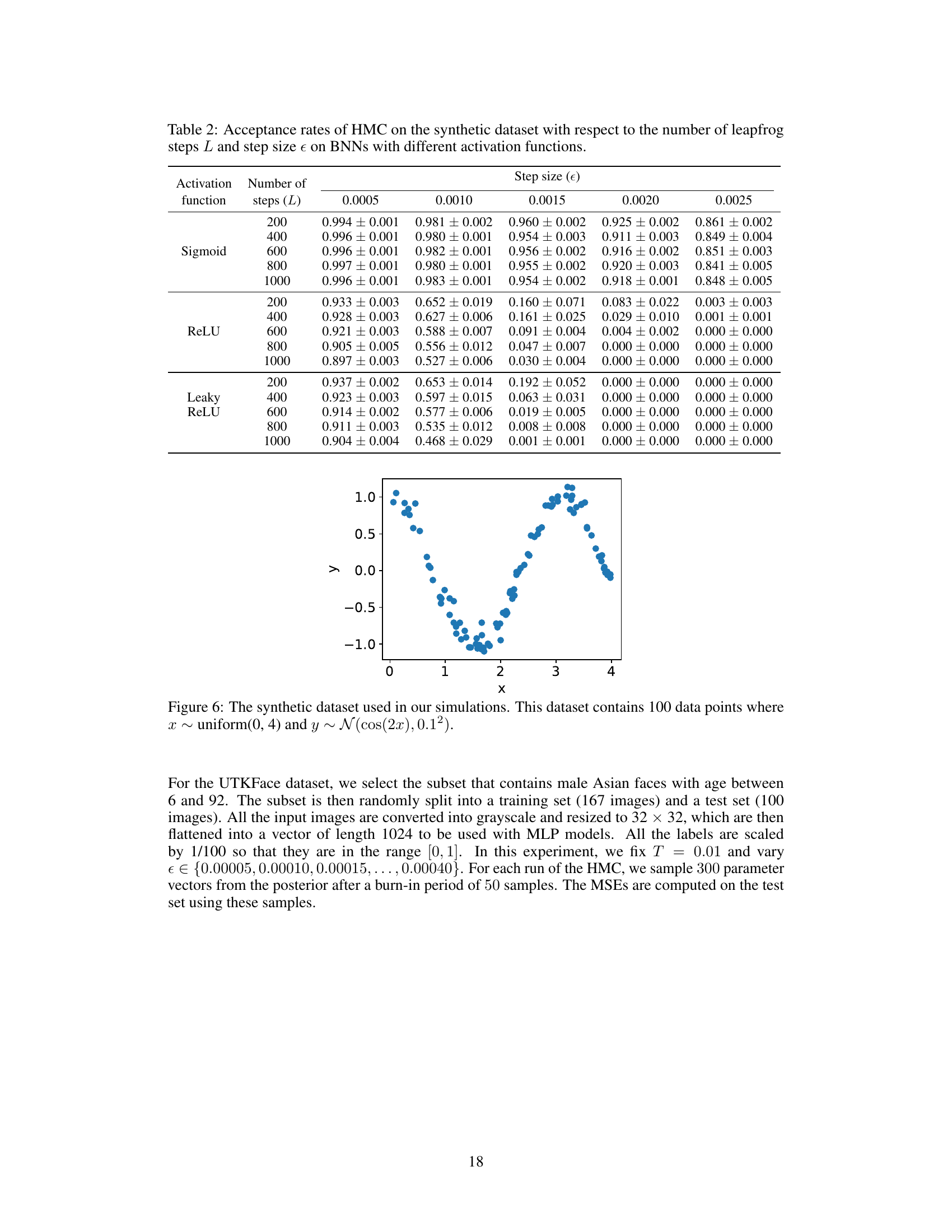
This figure shows a scatter plot of 100 data points generated from a cosine function with added Gaussian noise. The x-values are uniformly distributed between 0 and 4, and the y-values follow a normal distribution with a mean equal to the cosine of the corresponding x-value and a standard deviation of 0.1. This dataset is used in the paper’s experiments to compare the performance of Hamiltonian Monte Carlo (HMC) on Bayesian neural networks with different activation functions.
Full paper#