Geometry-aware training of factorized layers in tensor Tucker format

↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in deep learning and neural network optimization. It addresses the critical issue of reducing computational cost and memory footprint in training large neural networks by proposing a novel training method for factorized layers. The method’s theoretical guarantees, along with its practical effectiveness demonstrated through experiments, make it a significant advancement in model compression. This research opens new avenues for further investigations into geometry-aware optimization and adaptive rank methods for various tensor-based architectures. The method’s generality across tensor formats, demonstrated experimentally on various network architectures, greatly improves its wide applicability. This work is timely, providing efficient and robust training methods in a field increasingly challenged by the resource demands of large models.

Visual Insights

#

This figure compares the compression performance of TDLRT against various baselines (full model, matrix, Tucker, and CP decompositions) across four different model-dataset combinations: AlexNet and VGG16 on CIFAR-10, ResNet18 on CIFAR-10, and ResNet18 on Tiny-Imagenet. The x-axis represents the compression rate (%), and the y-axis represents the mean test accuracy (%). Each data point represents the average accuracy across 20 different random weight initializations. The figure demonstrates that TDLRT consistently achieves higher accuracy at higher compression rates compared to the baselines and exhibits lower variance across different initializations.

This table compares the performance of different model compression techniques on three different convolutional neural network architectures (Alexnet, VGG16, ResNet18) using the CIFAR10 dataset. The techniques include the proposed TDLRT method, along with several baseline methods involving matrix and tensor factorizations (CP, Tucker, Tensor Train, etc.), and pruning methods (SNIP, IMP, GraSP). For each architecture, the table shows the test accuracy and compression rate achieved by the best and second-best performing methods in each category.

In-depth insights

#

Tucker Geometry

#

Tucker Geometry, in the context of tensor decompositions and machine learning, refers to the geometric properties of the Tucker format, a way to represent tensors as a core tensor multiplied by a matrix along each mode. Understanding this geometry is crucial for efficient training, as the space of Tucker tensors forms a manifold with non-Euclidean properties; standard gradient descent methods are inefficient and prone to oscillations. Geometry-aware training, as explored in the paper, addresses these challenges by directly incorporating the manifold’s structure into the optimization process. This may involve projecting the gradient onto the tangent space of the manifold, using Riemannian optimization methods, or other techniques to account for the curvature and constraints. Rank adaptation, a key aspect of geometry-aware training, allows the algorithm to dynamically adjust the ranks of the Tucker decomposition during training, leading to efficient compression without significantly impacting performance. The theoretical underpinnings of geometry-aware training, particularly concerning convergence and approximation guarantees, are essential to establish its reliability and effectiveness. Therefore, studying Tucker Geometry provides valuable insights into designing efficient and robust training strategies for deep learning models with factorized layers.

Rank Adaptive Training

#

Rank adaptive training is a crucial technique for optimizing the efficiency and performance of deep learning models. It dynamically adjusts the rank of weight tensors during training, avoiding the need for pre-defined rank parameters which often lead to suboptimal performance. This adaptive approach, as described in the paper, is particularly valuable in addressing the challenges of layer factorization. It leverages the geometry of the underlying tensor space, performing updates along geodesics (shortest paths) on the manifold, which makes the algorithm less susceptible to the ill-conditioning often encountered near low-rank solutions. The paper highlights the advantages of this method through theoretical guarantees of loss descent and approximation quality, demonstrating superior compression rates and performance compared to traditional, fixed-rank training methodologies. Dynamic rank adjustment, a key feature of rank adaptive training, allows for efficient compression without sacrificing accuracy. The proposed algorithm achieves this through a robust mechanism that balances compression with model performance, adapting the rank in response to the training progress. This capability ensures a balance between computational efficiency and desired accuracy, significantly advancing the field of model compression.

Compression Rates

#

Analyzing compression rates in a research paper requires a nuanced understanding of the methodology. High compression rates are desirable, indicating efficient model representation, but should be viewed in conjunction with performance metrics. A drop in accuracy despite high compression suggests that the compression method sacrifices too much information. The paper likely evaluates the compression rate across different model architectures (e.g., AlexNet, VGG16, ResNet) and datasets (e.g., CIFAR10, ImageNet). Comparison to established baselines (e.g., full model, alternative factorization strategies) is crucial for determining the effectiveness of the proposed method. The results section might include tables and graphs visualizing the relationship between compression rate and performance (accuracy, loss). Furthermore, the discussion section should analyze the reasons behind variations in compression rates across different models or layers and explain how these rates relate to the structural properties of those components. A key aspect is the tradeoff between model size and performance: the paper will show whether a balance is reached or if a dramatic performance decrease offsets any gains in size reduction.

LoRA-like Adapters

#

The section on “LoRA-like Adapters” explores the application of the proposed low-rank Tucker decomposition method to the task of fine-tuning pre-trained models. Instead of training the entire model, low-rank adapters are added to the existing model weights, and these adapters are trained. This approach allows for efficient adaptation to new tasks without requiring extensive retraining of the full model. The authors demonstrate the method’s effectiveness on several benchmarks, showcasing comparable or even superior performance to other low-rank adaptation techniques like LoRA. A key advantage highlighted is the flexibility of the Tucker decomposition, handling both matrix and tensor-valued parameters effectively. The experimental results reveal substantial computational savings and improved efficiency in fine-tuning, particularly in cases involving higher-dimensional convolutional parameters, suggesting that the Tucker-based method is more suitable for larger and more complex models compared to the standard matrix-based LoRA.

Future Work

#

Future research could explore several promising avenues. Extending the geometry-aware training to other tensor decompositions beyond Tucker, such as CP or Tensor Train, could broaden applicability and potentially improve efficiency. Investigating the impact of different optimization algorithms and comparing them to SGD is crucial to better understand the method’s performance and robustness. A deeper theoretical analysis to establish tighter bounds on approximation error and convergence rates would strengthen the foundation. Finally, empirical evaluation on a wider range of architectures and datasets, particularly large-scale models, is necessary to demonstrate the practical impact and scalability of the approach. Exploring techniques to automate rank selection, potentially using meta-learning or reinforcement learning, would enhance the method’s ease of use and make it more widely accessible.

More visual insights

#

More on figures

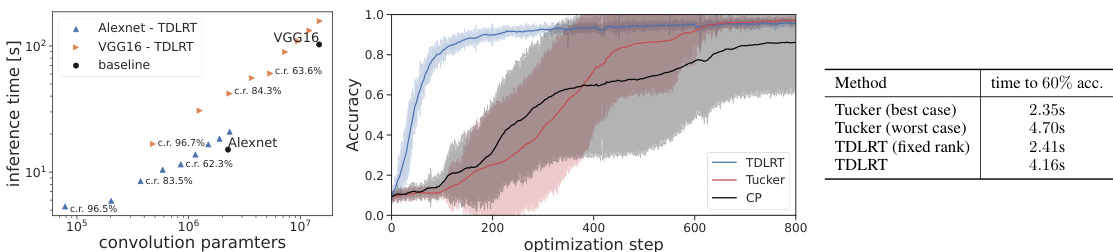
This figure compares the compression performance of the proposed TDLRT method against several baselines (full model, matrix, Tucker, and CP factorizations) on four different model architectures (AlexNet, VGG16, ResNet18 on CIFAR10, and ResNet18 on TinyImagenet). The x-axis represents the compression rate (percentage of parameters removed), and the y-axis represents the mean accuracy across 20 different random weight initializations. The error bars illustrate the variance in accuracy across these initializations. The figure shows that TDLRT generally achieves higher accuracy at higher compression rates compared to other methods, and also exhibits less variance across different initializations.

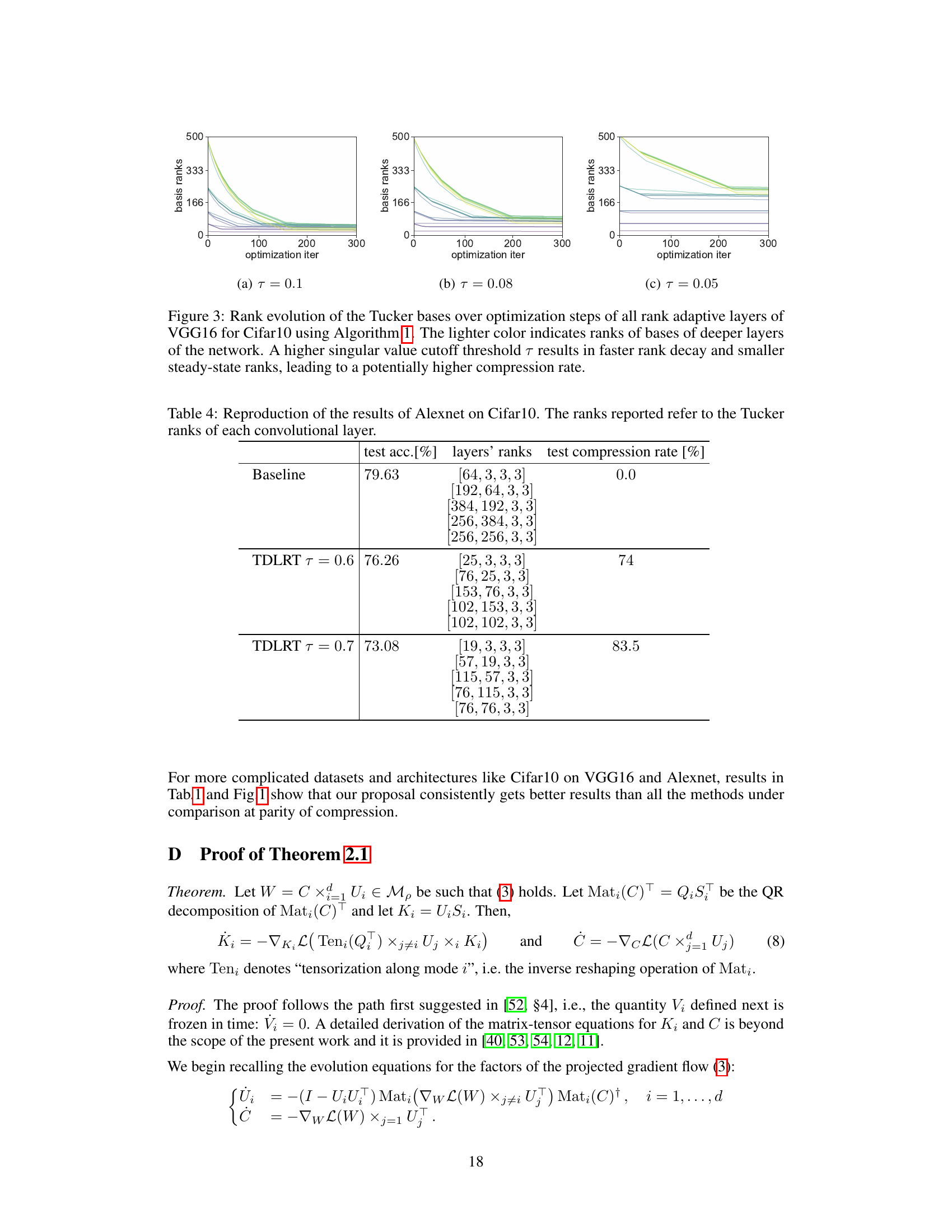
This figure shows how the ranks of Tucker bases evolve during the optimization process for different singular value cutoff thresholds (τ). Lighter colors represent bases closer to the output layer of the VGG16 network. Higher thresholds (τ) lead to faster rank decay and lower steady-state ranks, resulting in higher compression rates. The figure demonstrates the rank-adaptive nature of Algorithm 1.

More on tables

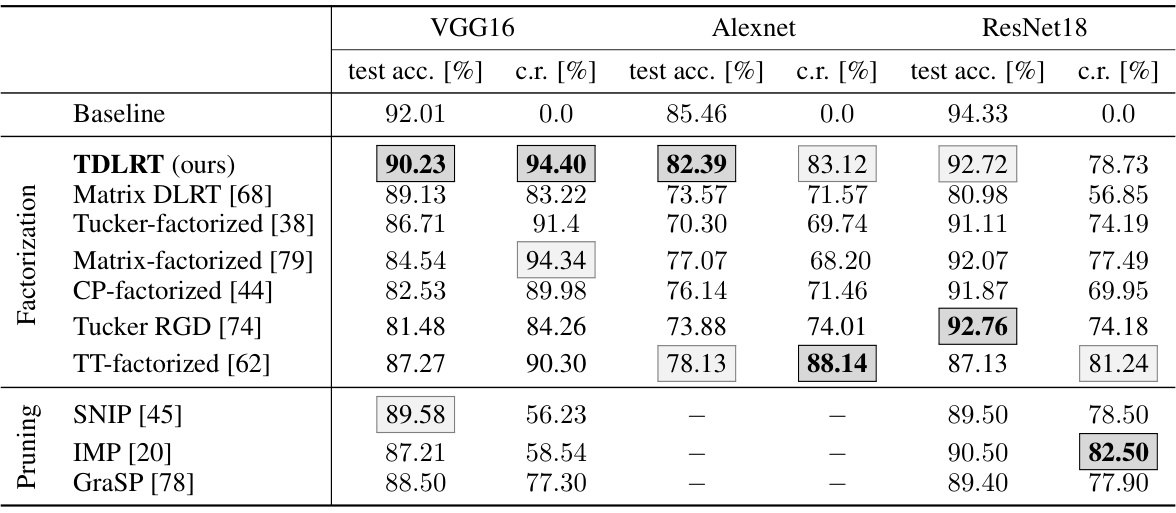
This table compares the best compression rate achieved by different model compression methods on three different CNN architectures (Alexnet, VGG16, and ResNet18) using the CIFAR10 dataset. The compression rate is calculated as 1 - c/f, where c is the number of convolutional parameters in the compressed model and f is the number of convolutional parameters in the full model. The table shows that TDLRT (the proposed method) achieves the highest compression rates with comparable accuracy to the other methods. Different baseline methods include direct training of low-rank matrix and tensor factorizations, and pruning techniques based on weight sparsification.

This table compares the performance of the proposed TDLRT method against LoRA for fine-tuning pre-trained models on two different tasks: the GLUE benchmark (a natural language understanding benchmark) and Stable Diffusion Dreambooth (an image generation model). It shows the loss and the number of parameters for different rank settings for both LoRA and the proposed method. The results demonstrate the comparable performance of TDLRT to LoRA while achieving better compression.

This table presents the results of the ResNet18 model trained on the Tiny-Imagenet dataset, comparing the performance of TDLRT with different compression rates (controlled by the parameter τ) against a standard Tucker factorization baseline. It shows that TDLRT achieves a higher compression rate while maintaining a competitive test accuracy, demonstrating its effectiveness in model compression.

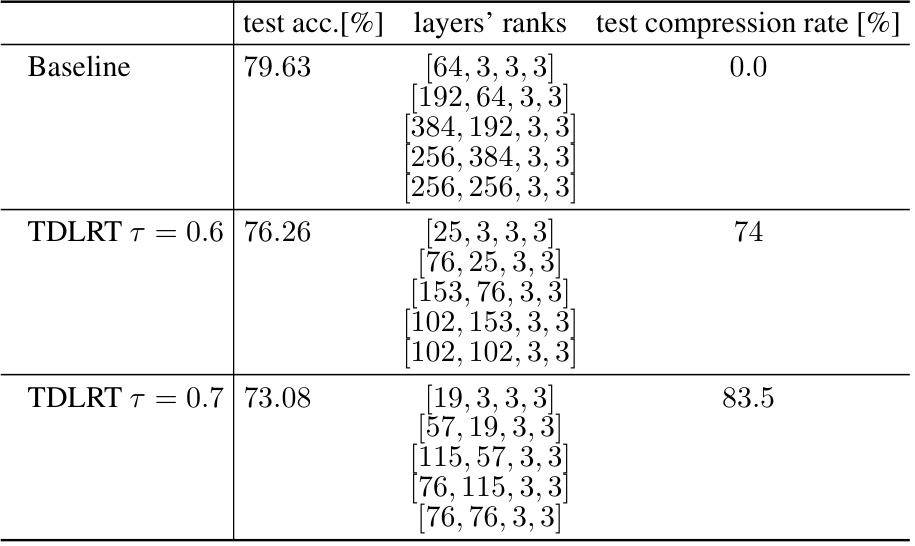
This table compares the test accuracy and Tucker ranks of each convolutional layer for Alexnet trained on Cifar10 dataset, using both the baseline (full model) and TDLRT approaches with different compression rates (τ). The Tucker ranks show the compression achieved by the TDLRT method on each layer.

Full paper

#