↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Traditional federated learning (FL) struggles with hierarchical architectures and non-i.i.d. data, leading to model drift at multiple levels. Existing HFL algorithms don’t efficiently correct this multi-timescale drift, limiting their performance and theoretical guarantees.
The paper proposes a novel multi-timescale gradient correction (MTGC) method to mitigate model drift. MTGC introduces coupled correction terms to address drift at both client and group levels. It’s theoretically proven to converge under general non-convex settings, immune to data heterogeneity, and exhibits linear speedup. Extensive experiments validated MTGC’s superior performance compared to existing baselines across diverse HFL settings.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on hierarchical federated learning (HFL). It addresses the significant challenge of multi-timescale model drift in non-i.i.d. data settings, a problem largely unsolved by existing HFL methods. The proposed MTGC algorithm offers a provably stable solution with a proven convergence bound, opening new avenues for designing robust and efficient HFL systems. The provided codebase further enhances its accessibility and impact.
Visual Insights#
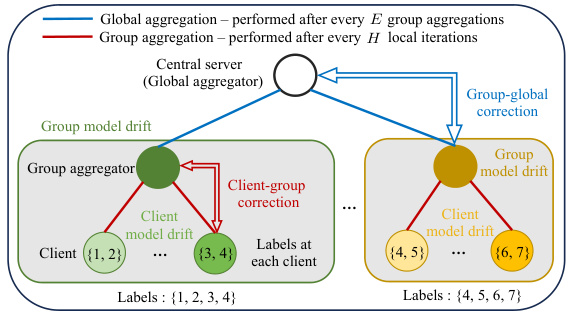
This figure illustrates the hierarchical federated learning (HFL) architecture with multi-timescale gradient correction (MTGC). The figure shows a central server (global aggregator) connected to multiple group aggregators, each responsible for aggregating models from a group of clients. Each client has its own local dataset, and non-i.i.d. data is present both within client groups (intra-group) and between groups (inter-group). MTGC introduces two types of gradient corrections: client-group correction to reduce model drift among clients within a group and group-global correction to further reduce model drift across groups, addressing the multi-timescale model drift challenge.
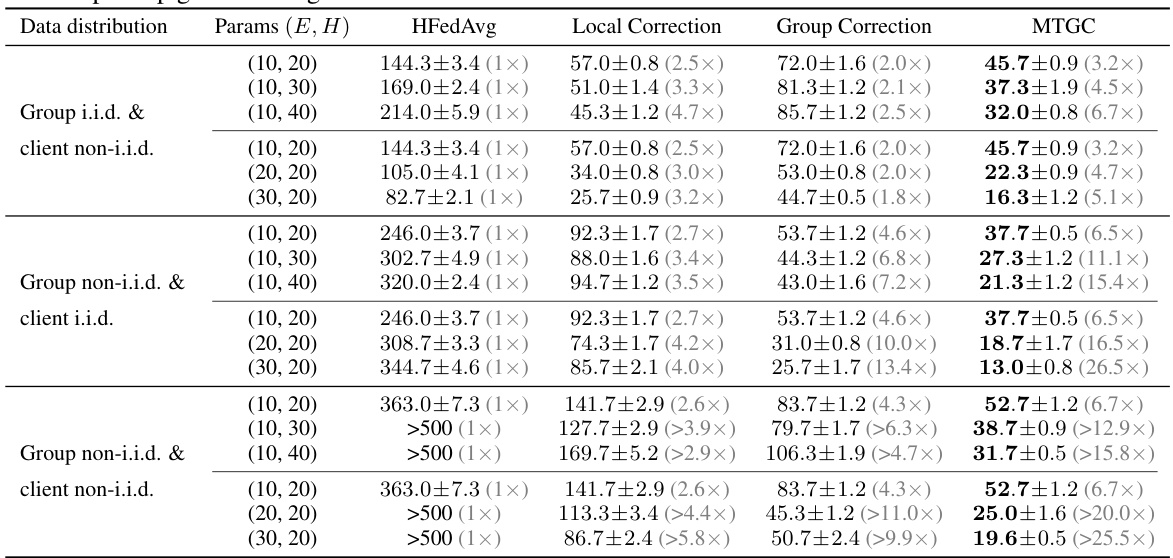
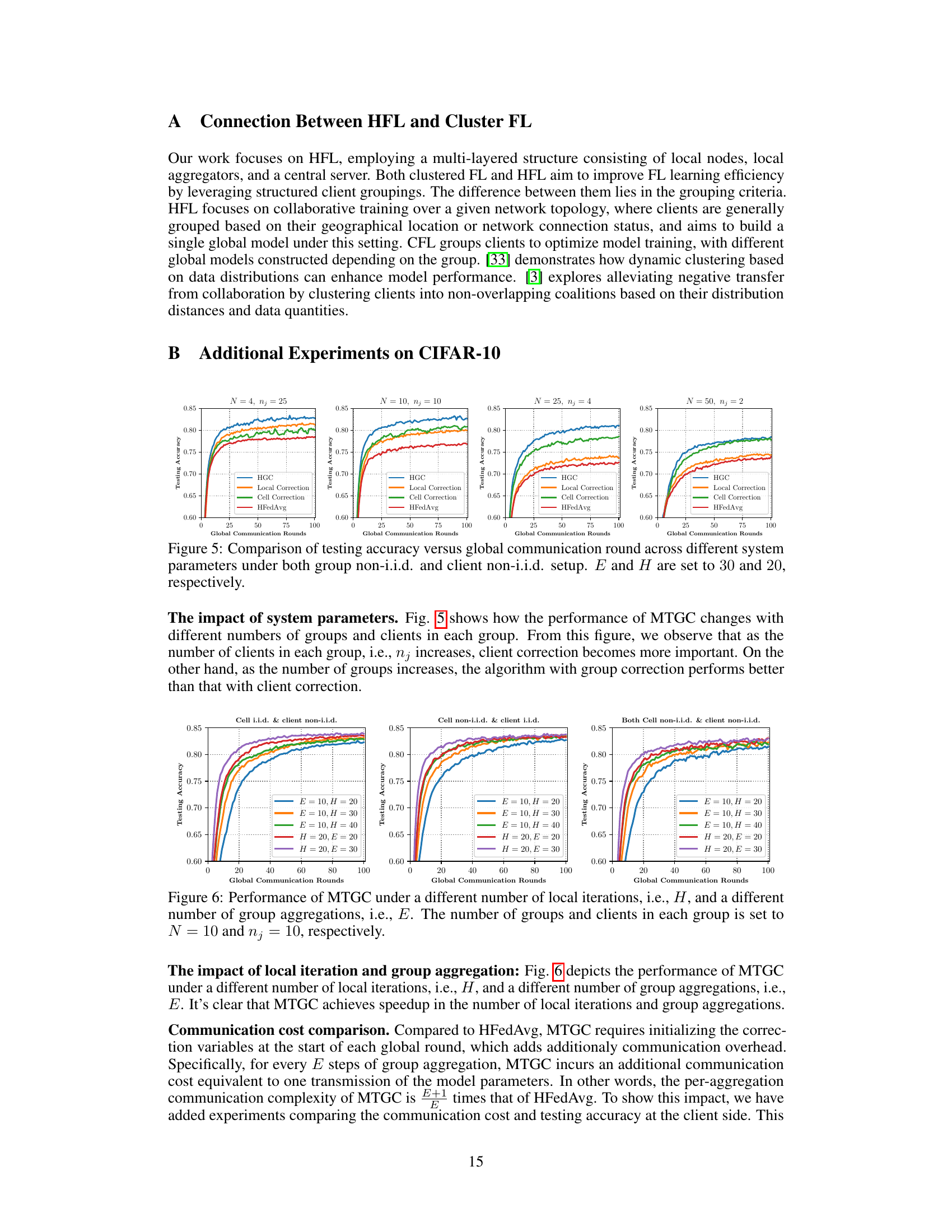
This table shows the number of global rounds needed by different federated learning algorithms (HFedAvg, Local Correction, Group Correction, and MTGC) to reach 80% testing accuracy on the CIFAR-10 dataset under various data distribution scenarios and aggregation period settings (E and H). It highlights MTGC’s superior performance and improved speedup with increasing E and H values. Standard deviations across 3 trials are included.
In-depth insights#
Multi-Timescale Drift#
In hierarchical federated learning (HFL), multi-timescale drift is a critical challenge arising from the inherent heterogeneity and asynchronous updates across multiple levels of the hierarchy. Unlike traditional FL, where model drift primarily occurs between the central server and clients, HFL introduces additional drift between local clients and group aggregators, as well as between group aggregators and the global aggregator. These drifts occur at different timescales due to varying communication frequencies and update periods at each level. The frequency of updates decreases as we move up the hierarchy, exacerbating the issue. Data heterogeneity at each level further compounds the problem, as different data distributions across clients and groups lead to models diverging from the global optimum. This divergence at different levels and timescales necessitates novel algorithmic solutions that can effectively correct for multi-timescale drift without overly increasing communication overhead. Addressing multi-timescale drift requires careful consideration of how to design update rules and correction mechanisms that are sensitive to the dynamics of model updates at each hierarchical level and the corresponding timescale. Therefore, understanding and mitigating multi-timescale drift is essential for designing robust and efficient HFL algorithms.
MTGC Algorithm#
The MTGC (Multi-Timescale Gradient Correction) algorithm is a novel approach designed for hierarchical federated learning (HFL) environments. Its core innovation lies in addressing the challenges of multi-timescale model drift, a phenomenon where inconsistencies arise in model updates across different levels of a hierarchical system. MTGC tackles this by introducing coupled gradient correction terms: client-group correction and group-global correction. The client-group correction refines client gradients toward their group’s consensus, mitigating local data heterogeneity. Simultaneously, group-global correction aligns group gradients with the global model, thereby addressing inconsistencies between groups. A key strength of MTGC is its ability to handle non-i.i.d. data effectively across multiple levels, a significant improvement over existing HFL algorithms. The algorithm’s effectiveness is validated through theoretical analysis demonstrating convergence under general non-convex settings and extensive empirical results showing superior performance across varied datasets and models. The adaptive nature of the corrections, coupled with the multi-timescale update strategy, allows MTGC to dynamically adjust to varying levels of data heterogeneity without requiring frequent model aggregations, leading to improved communication efficiency.
Convergence Bound#
The convergence bound analysis is crucial for evaluating the efficacy and stability of any iterative algorithm, especially in complex settings like hierarchical federated learning (HFL). A tight convergence bound provides a theoretical guarantee on the algorithm’s performance and helps understand its limitations. In the context of HFL, a good convergence bound should ideally demonstrate linear speedup with the number of clients, local iterations, and group aggregations, showcasing scalability. It should also be robust against data heterogeneity, proving its efficacy even when data distributions differ significantly across clients and groups. Non-convex settings, which are prevalent in many real-world machine learning tasks, necessitate analysis beyond simple convex assumptions to show practicality. The analysis must address challenges related to the coupling of correction terms that frequently appear in HFL algorithms for mitigating data heterogeneity, confirming the algorithm’s stability in such conditions. Finally, an ideal convergence bound would explicitly show how the theoretical guarantee recovers the conventional results when simplified to a single-level FL structure, providing assurance of its generalizability and efficacy across various setups.
HFL Experiments#
In a hypothetical research paper section titled “HFL Experiments,” a thorough evaluation of hierarchical federated learning (HFL) would be expected. This would involve a systematic exploration of various aspects of HFL algorithms. The experiments should cover different datasets to assess the robustness of the methods under varied data distributions, including scenarios with varying degrees of heterogeneity across clients and groups. Performance metrics like accuracy, convergence speed, and communication overhead should be meticulously recorded and analyzed. Ablation studies would be crucial to isolate the effects of different components of the proposed HFL algorithm, helping determine the contribution of each component. The analysis should go beyond simple comparisons against existing FL algorithms, potentially including a comprehensive comparison against other HFL approaches to establish the novelty and improvements. Statistical significance of all experimental results should be rigorously evaluated using appropriate statistical tests. The experiments should be designed to answer specific research questions related to the capabilities and limitations of the proposed HFL techniques under diverse real-world conditions. Furthermore, a discussion of the practical challenges and insights gained from the experimental process would enhance the value of this section.
Future of HFL#
The future of hierarchical federated learning (HFL) is bright, but filled with challenges. Addressing multi-timescale model drift remains a critical area; techniques like the multi-timescale gradient correction (MTGC) presented in this paper offer a promising starting point, but further research is needed to create more robust and efficient methods, especially for non-convex settings and highly heterogeneous data. Scalability is another key concern; as HFL systems grow larger and more complex, new algorithms and architectures that can efficiently manage communication and aggregation across multiple layers are crucial. Security and privacy will also continue to be major focus areas, given the distributed nature of HFL; research into secure aggregation techniques and privacy-preserving mechanisms are needed to enable wide-spread adoption. Finally, theoretical understanding must advance; rigorous convergence analysis that accurately captures the complexities of HFL systems under various scenarios is needed to guide algorithm design and optimization. Overall, a multi-disciplinary approach incorporating advancements in distributed optimization, network science, cryptography and privacy will shape the future of HFL, paving the way for truly decentralized, large-scale machine learning.
More visual insights#
More on figures

This figure illustrates the local update process in hierarchical federated learning (HFL) scenarios with and without gradient correction. (a) shows the situation without gradient correction, where each client model converges towards its own local optimum. (b) demonstrates client-group correction, where the model updates are adjusted towards the group optimum. (c) showcases the multi-timescale gradient correction (MTGC) method proposed in the paper, which effectively corrects the client gradients towards both the group and global optima, leading to improved convergence.

This figure illustrates the hierarchical federated learning (HFL) architecture with multi-timescale gradient correction (MTGC). The system comprises clients grouped into multiple groups, each coordinated by a group aggregator node. The group aggregators, in turn, communicate with a central server. MTGC introduces coupled gradient correction terms to address model drift at different levels of the hierarchy (client-group and group-global corrections). These corrections aim to improve model convergence in the presence of multi-level non-i.i.d. data by guiding the clients’ model updates to align better with both group and global objectives.
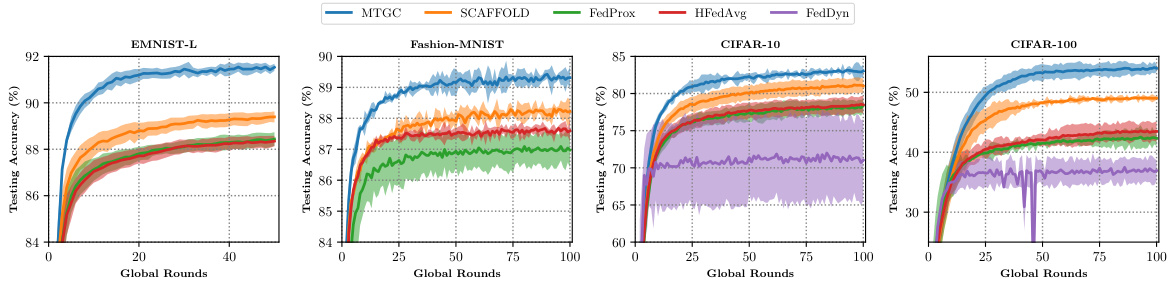
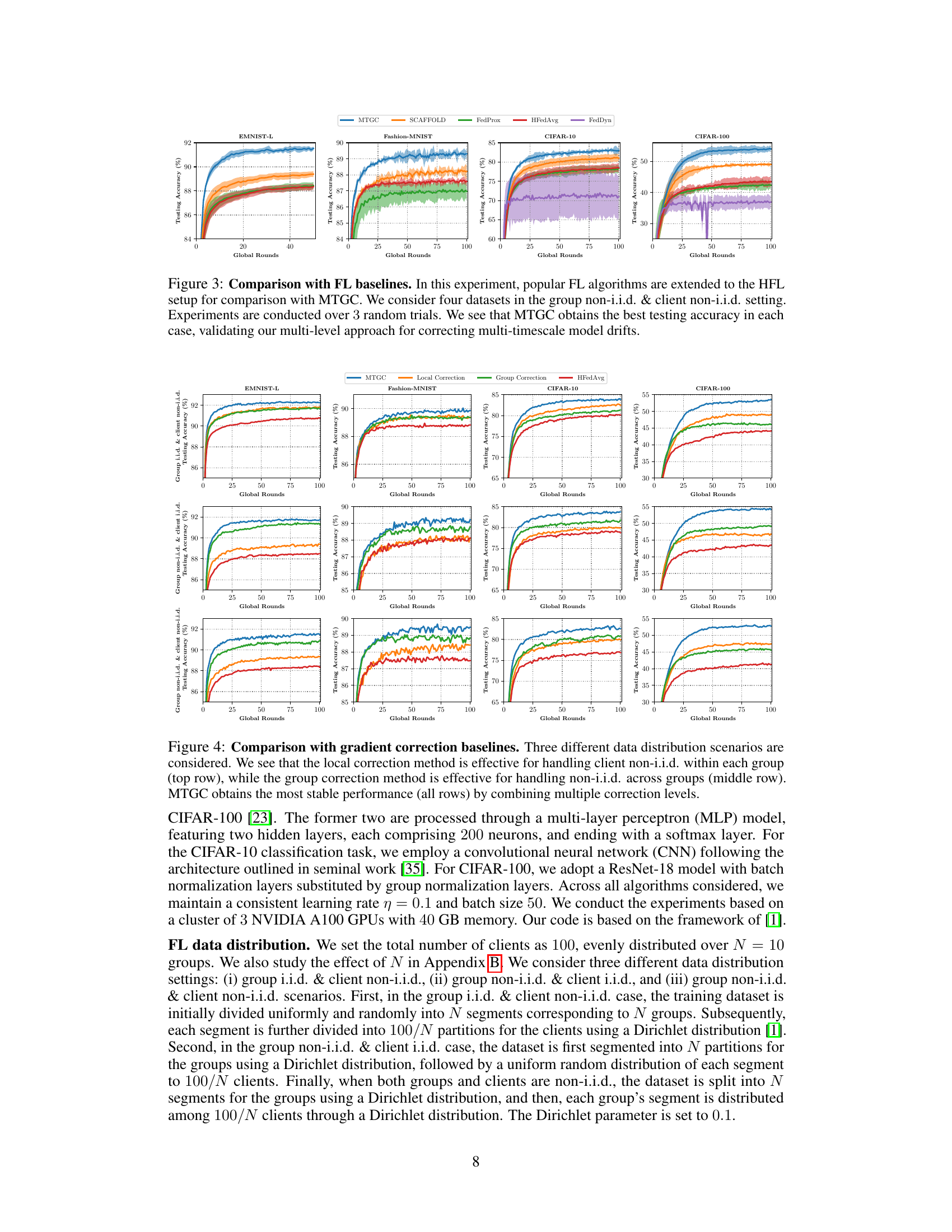
The figure compares the performance of MTGC with several other popular federated learning (FL) algorithms (SCAFFOLD, FedProx, HFedAvg, and FedDyn) on four different datasets (EMNIST-Letters, Fashion-MNIST, CIFAR-10, and CIFAR-100). The experiments are conducted under a non-i.i.d. setting at both the group and client level. The results show that MTGC consistently outperforms the other methods in terms of testing accuracy across all datasets, demonstrating its effectiveness in handling multi-timescale model drift in hierarchical federated learning (HFL) settings.

This figure compares the performance of MTGC against baselines that use only client-level correction or only group-level correction. Three different data heterogeneity scenarios are evaluated: group i.i.d. and client non-i.i.d.; group non-i.i.d. and client i.i.d.; and group non-i.i.d. and client non-i.i.d. The results demonstrate that MTGC, by employing both client-level and group-level corrections, outperforms the baselines in all scenarios, achieving the most consistent and stable results.

This figure compares the performance of MTGC against three baseline methods under different data heterogeneity scenarios: group i.i.d. & client non-i.i.d., group non-i.i.d. & client i.i.d., and group non-i.i.d. & client non-i.i.d. Each row represents a scenario. The columns represent different datasets. The baseline methods are: HFedAvg (without correction), Local Correction (only correcting client-level drift), and Group Correction (only correcting group-level drift). MTGC combines both local and group corrections and is shown to be the most effective and stable across the board.

This figure compares the performance of MTGC against three baseline methods under three different data distribution scenarios: group i.i.d. & client non-i.i.d., group non-i.i.d. & client i.i.d., and group non-i.i.d. & client non-i.i.d. The baseline methods are HFedAvg (without correction), HFedAvg with local correction, and HFedAvg with group correction. The figure demonstrates that the local correction is effective for client-level non-i.i.d., the group correction for group-level non-i.i.d., and that MTGC combines these to achieve the most stable performance in all cases.

This figure illustrates the multi-timescale gradient correction (MTGC) method for handling multi-level non-i.i.d. data in hierarchical federated learning (HFL). It shows a hierarchical architecture with a central server, group aggregators, and clients. The figure highlights the multi-timescale model drift occurring across different hierarchical levels and how MTGC corrects client model drift towards the group gradient and group gradient towards the global gradient. Client-group correction and group-global correction terms are introduced to mitigate these drifts.
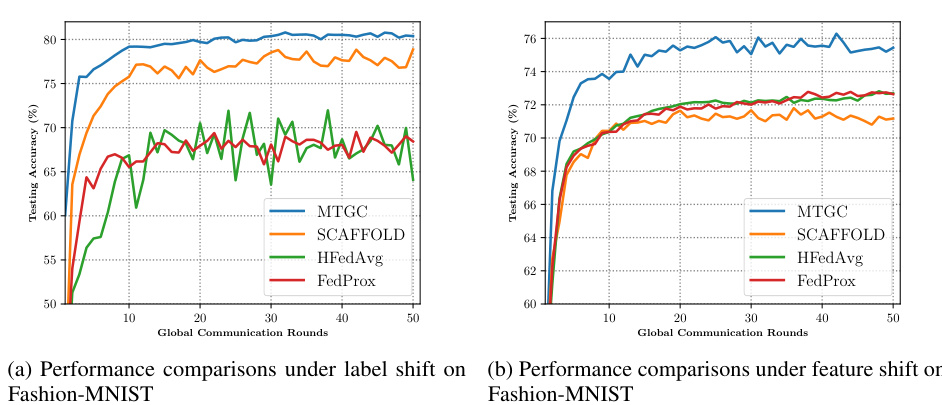
This figure compares the performance of MTGC against three baselines in three different data distribution scenarios: (i) group i.i.d. & client non-i.i.d., (ii) group non-i.i.d. & client i.i.d., and (iii) group non-i.i.d. & client non-i.i.d.. Each row represents one scenario. The baselines are: HFedAvg (no correction), Local Correction (only client-group correction), and Group Correction (only group-global correction). The figure shows that MTGC is most stable and provides the best accuracy by combining both client-group and group-global corrections.
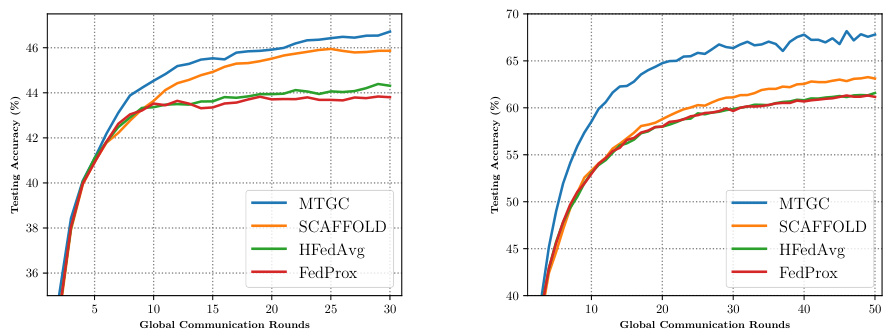
This figure compares the performance of MTGC against four other popular Federated Learning (FL) algorithms (SCAFFOLD, FedProx, FedDyn, and HFedAvg) on four different datasets (EMNIST-Letters, Fashion-MNIST, CIFAR-10, and CIFAR-100). The experiments simulate a hierarchical FL setting where data is non-identically distributed across both groups and individual clients, representing real-world challenges. The results show that MTGC consistently achieves the highest testing accuracy, showcasing its effectiveness in handling multi-timescale model drift inherent in hierarchical federated learning.

This figure illustrates the multi-timescale gradient correction (MTGC) method for handling multi-level non-i.i.d. data in hierarchical federated learning (HFL). It shows a hierarchical architecture with a central server, group aggregators, and individual clients. The key idea is to introduce coupled gradient correction terms at multiple levels to address client model drift (caused by local updates) and group model drift (caused by federated averaging within groups). These corrections help each client’s model converge towards a better global model, even with data heterogeneity across multiple levels.

This figure illustrates the multi-timescale gradient correction (MTGC) methodology for handling multi-level non-i.i.d. data in hierarchical federated learning (HFL). It shows a hierarchical structure with a central server, group aggregators, and clients. The figure highlights the concept of multi-timescale model drift occurring across multiple levels. It also visually represents the key idea of MTGC, which introduces coupled gradient correction terms (client-group correction and group-global correction) to address this drift at different timescales.
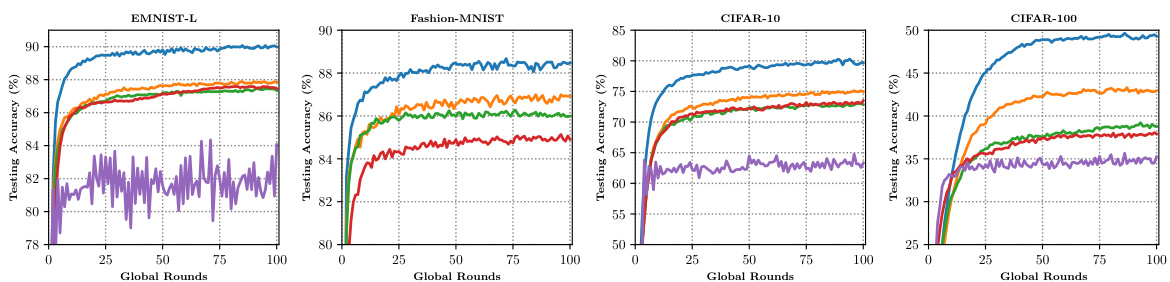
This figure compares the performance of MTGC against four other federated learning (FL) algorithms (SCAFFOLD, FedProx, HFedAvg, and FedDyn) on four different datasets (EMNIST-Letters, Fashion-MNIST, CIFAR-10, and CIFAR-100). Each algorithm was adapted for hierarchical federated learning (HFL). The results, averaged over three trials, show that MTGC achieves the highest testing accuracy on all datasets, highlighting its effectiveness in correcting multi-timescale model drifts in HFL.
Full paper#