↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many private data analysis algorithms struggle with the “curse of dimensionality,” exhibiting high costs. However, many datasets possess inherent low-dimensional structures, which are often not exploited by DP algorithms. This paper tackles this challenge by focusing on subspace estimation, a crucial task in various applications such as machine learning and data mining, where DP algorithms typically face a significant dependence on input dimensionality. The challenge is identifying when reduced points are sufficient and necessary, and measuring a given datasets “easiness”.
This research introduces new measures quantifying dataset easiness for private subspace estimation by using multiplicative singular-value gaps. The study supports these measures with new upper and lower bounds, effectively demonstrating the first gap types sufficient and necessary for dimension-independent subspace estimation. The authors further develop a practical algorithm reflecting their upper bounds, showcasing its effectiveness in high-dimensional scenarios, thus, significantly improving the efficiency and accuracy of DP subspace estimation.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on differentially private (DP) algorithms and high-dimensional data analysis. It offers novel measures of data easiness and efficient algorithms that significantly reduce the computational cost of DP algorithms. This directly addresses the major challenges in DP, opening new avenues for research and applications in various fields including machine learning and data mining.
Visual Insights#
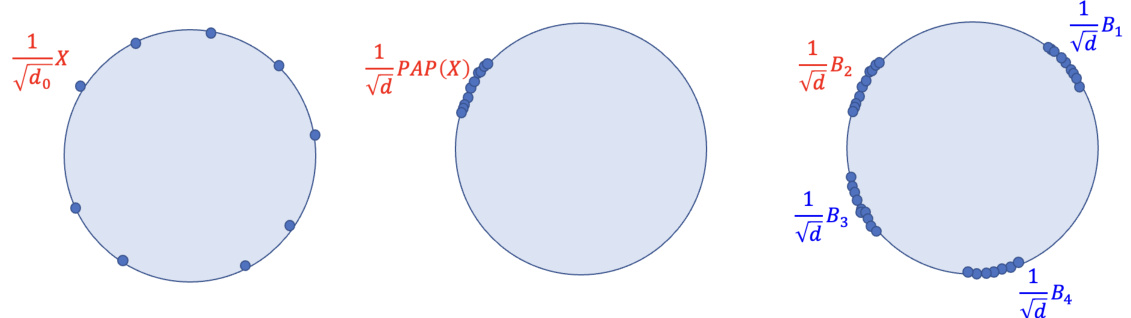
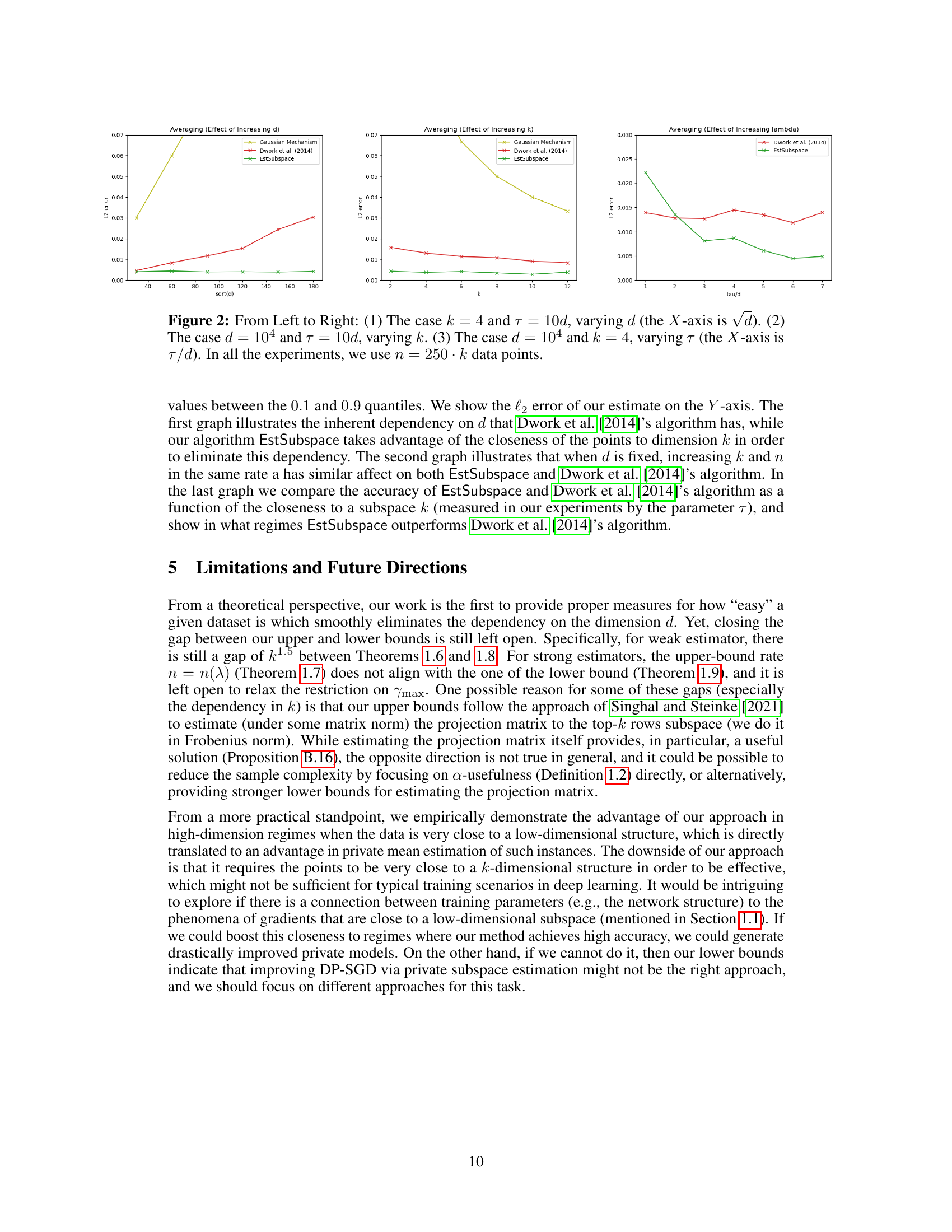
This figure illustrates the process of generating hard instances for DP subspace estimation using the padding-and-permuting (PAP) technique. Starting with well-spread points on a low-dimensional sphere, the PAP technique adds padding and permutes the columns, resulting in points clustered close together on a higher-dimensional sphere. This process is repeated k times, creating k groups of points with one group containing the original data embedded in it. Reducing the parameter ‘a’ further increases the point clustering, thus making them closer to a k-dimensional subspace, representing ’easy’ instances for the algorithm.
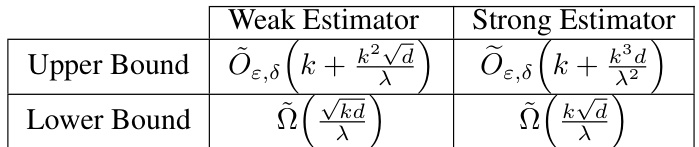
This table summarizes the upper and lower bounds on the number of points (n) required for differentially private subspace estimation, categorized by whether a weak or strong subspace estimator is used. The bounds are expressed in terms of the rank of the subspace (k), the dimension of the ambient space (d), and the accuracy parameter (λ). Note that the restrictions on ymax and λ are ignored for simplicity of presentation.
Full paper#