TL;DR#
Low-bit quantization is crucial for deploying advanced image super-resolution (SR) models on resource-constrained devices. However, it often leads to significant accuracy loss, especially in transformer-based models. Existing post-training quantization (PTQ) methods struggle to maintain accuracy when reducing the bit-width of these models.
The paper introduces 2DQuant, a dual-stage PTQ method that overcomes these challenges. The first stage, Distribution-Oriented Bound Initialization (DOBI), efficiently determines initial quantizer bounds based on data distribution. The second stage, Distillation Quantization Calibration (DQC), refines these bounds by training the quantized model to mimic its full-precision counterpart using distillation. 2DQuant significantly outperforms existing PTQ methods across various metrics and achieves impressive compression and speedup ratios.
Key Takeaways#
Why does it matter?#
This paper is important because it presents 2DQuant, a novel method for low-bit post-training quantization of image super-resolution models. This addresses the significant accuracy degradation typically associated with low-bit quantization in transformer-based models, a crucial problem for deploying advanced SR models on resource-constrained devices. The proposed method’s superior performance, especially in achieving high PSNR improvements, opens new avenues for efficient and accurate model compression in computer vision.
Visual Insights#

🔼 This figure visually compares the results of different image super-resolution (SR) methods on a sample image from the Urban100 dataset. It highlights the blurring artifacts produced by existing methods (Percentile [27], DBDC+Pac [41]) compared to the sharp, detailed reconstruction of the proposed method (Ours) and the full-precision (FP) model. The ground truth high-resolution image (HR) is also shown for reference. This demonstrates that the authors’ approach significantly improves the visual quality of SR, particularly in terms of artifact reduction.
read the caption
Figure 1: Existing methods suffer from blurring artifacts.

🔼 This table compares the model complexity (number of parameters and floating-point operations) and performance (PSNR on Urban100 dataset) of different super-resolution models. It shows how various models, including EDSR, a quantized version of EDSR, SwinIR-light, and a quantized version using the DBDC+Pac method, compare to the proposed 4-bit quantized model (Ours). The comparison highlights the efficiency gains achieved with low-bit quantization and the effectiveness of the proposed method.
read the caption
Table 1: Complexity and performance (×4).
In-depth insights#
2DQuant: Low-bit PTQ#
The heading “2DQuant: Low-bit PTQ” suggests a novel post-training quantization (PTQ) method for reducing the bit-width of a model, particularly focusing on low-bit representations (e.g., 2-bit, 4-bit). The name “2DQuant” hints at a two-dimensional or dual-stage approach to quantization, likely involving separate strategies for weights and activations. This dual-stage process may involve initial bound setting for the quantizers followed by a refinement stage. Low-bit PTQ is crucial for deploying advanced image super-resolution (SR) models on resource-constrained devices, as it allows significant storage compression and speed improvements. The effectiveness of 2DQuant would likely be measured by the trade-off between accuracy loss (compared to full-precision models) and the compression ratio achieved. A successful 2DQuant method would demonstrate superior performance to existing PTQ techniques, particularly for transformer-based SR models, which often suffer from greater accuracy degradation with low-bit quantization.
DOBI & DQC Methods#
The paper introduces DOBI (Distribution-Oriented Bound Initialization) and DQC (Distillation Quantization Calibration) as a two-stage post-training quantization method. DOBI cleverly addresses the challenge of asymmetric activation distributions in transformer-based models by employing a fast MSE-based search to find optimal bounds for quantizers, avoiding the inefficiency of methods which are unsuitable for such distributions. This is particularly important as asymmetric distributions lead to poor parameter homogenization in quantized models. Following DOBI, DQC further refines the quantizer parameters by using a knowledge distillation approach. This allows the quantized model to learn from its full-precision counterpart, effectively minimizing the performance gap caused by quantization and leading to improved accuracy. The combined approach of DOBI and DQC forms the core of 2DQuant, enabling efficient and accurate low-bit quantization of image super-resolution models.
Transformer Quantization#
Transformer quantization presents a unique challenge due to the architecture’s inherent complexity. Naive quantization techniques often lead to significant performance degradation in transformer-based models, especially those employed in image super-resolution. This is because transformers rely heavily on precise floating-point calculations within the self-attention mechanism and other matrix operations. Quantization introduces errors that disrupt the delicate balance required for accurate feature extraction and subsequent high-resolution image reconstruction. Therefore, effective quantization methods must carefully consider the unique distribution of weights and activations within the transformer network. Advanced techniques such as distribution-aware quantization and quantization-aware training are crucial for mitigating the adverse effects of quantization while maintaining reasonable accuracy. Further research should explore novel quantization strategies tailored to specific layers or modules within the transformer architecture to maximize compression while minimizing performance loss. Hardware-aware quantization is also a promising area that considers the specific capabilities and limitations of target hardware platforms.
Ablation Study Results#
An ablation study for a research paper on image super-resolution would systematically remove components of the proposed method to assess their individual contributions. Results would show the impact of each component on key metrics like PSNR and SSIM. A thoughtful analysis would go beyond simply reporting metric changes. It would explore how the removal of each module affected the model’s ability to handle various image characteristics, such as textures, edges, and noise. Furthermore, a visual comparison of output images would provide qualitative insights, helping to understand whether the quantitative metrics fully capture the impact on image quality. The study should also consider the trade-offs between model complexity and performance. For example, eliminating a module might lead to a simpler model, but at a cost of reduced accuracy. Ultimately, the results section would demonstrate a compelling case for the necessity of each component in achieving optimal super-resolution, supporting the overall claims of the paper.
Future Research Gaps#
Future research could explore extending 2DQuant’s effectiveness to other image processing tasks beyond super-resolution, such as denoising or deblurring. Investigating the impact of different network architectures beyond the Transformer-based SwinIR, especially CNNs and hybrid models, would offer valuable insights into the algorithm’s generalizability. A deeper dive into the theoretical underpinnings of 2DQuant, potentially developing a more rigorous mathematical framework to explain its superior performance, is warranted. Improving the efficiency of the DOBI search algorithm could further accelerate the quantization process. Finally, addressing the limitation of requiring a calibration dataset for optimal performance would enhance practicality for real-world deployment.
More visual insights#
More on figures

🔼 This figure illustrates the two-stage process of the 2DQuant method for post-training quantization. The first stage, Distribution-Oriented Bound Initialization (DOBI), uses two strategies to efficiently find a coarse clipping bound for weight and activation quantization. The second stage, Distillation Quantization Calibration (DQC), further refines these bounds by training the quantized model to mimic the behavior of its full-precision counterpart, ensuring that both intermediate features and final outputs closely match. This two-step approach aims to balance speed and accuracy in low-bit quantization.
read the caption
Figure 2: The overall pipeline of our proposed 2DQuant method. The whole pipeline contains two stages, optimizing the clipping bound from coarse to fine. In stage 1, we design DOBI to efficiently obtain the coarse bound. In stage 2, DQC is performed to finetune clipping bounds and guarantee the quantized model learns the full-precision (FP) model's feature and output information.
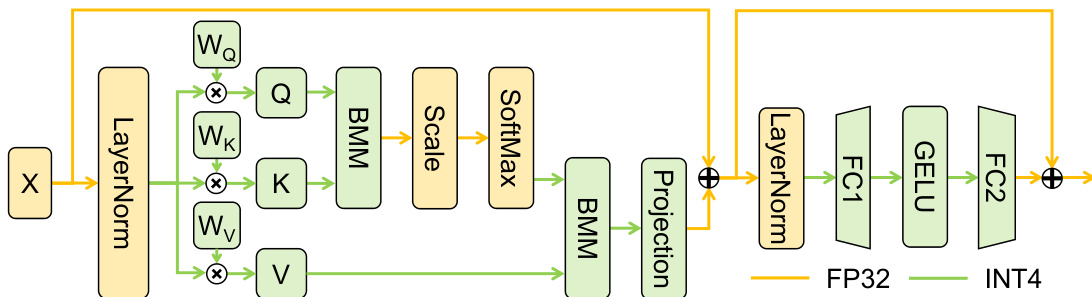
🔼 This figure illustrates how the quantization scheme is applied to the SwinIR Transformer blocks. The process involves applying fake quantization and integer arithmetic to computationally intensive operations such as linear layers and batch matrix multiplications. The scheme can handle lower bit depths (3 or 2 bits) and ignores dropout operations in attention and projection layers. It shows the flow of data through the various stages of the block, highlighting which parts are processed using full-precision floating-point (FP32) and which parts are processed using integer arithmetic (INT4).
read the caption
Figure 3: Quantization scheme for SwinIR Transformer blocks. Fake quantization and INT arithmetic are performed in all compute-intensive operators including all linear layers and batch matmul. Lower bits such as 3 or even 2 are also permitted. Dropout of attention and projection is ignored

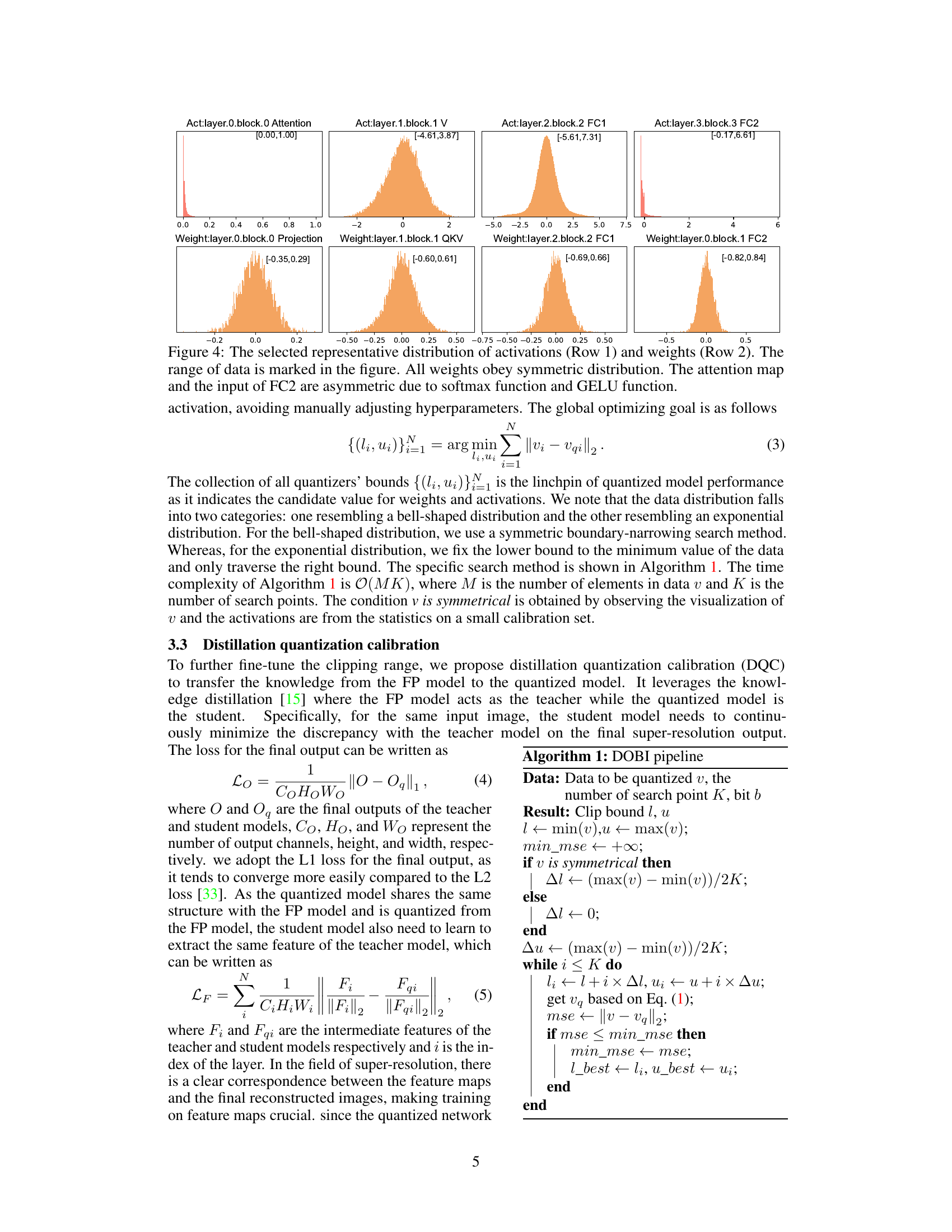
🔼 This figure visualizes the distributions of activations and weights in different layers of the SwinIR Transformer model. The top row shows the distributions of activations, highlighting the differences in distribution shapes (symmetric vs. asymmetric) for different layers and their activation functions (Softmax, GELU). The bottom row shows the distributions of weights, which are generally symmetric around zero for all linear layers. The range of values for each distribution is indicated.
read the caption
Figure 4: The selected representative distribution of activations (Row 1) and weights (Row 2). The range of data is marked in the figure. All weights obey symmetric distribution. The attention map and the input of FC2 are asymmetric due to softmax function and GELU function.
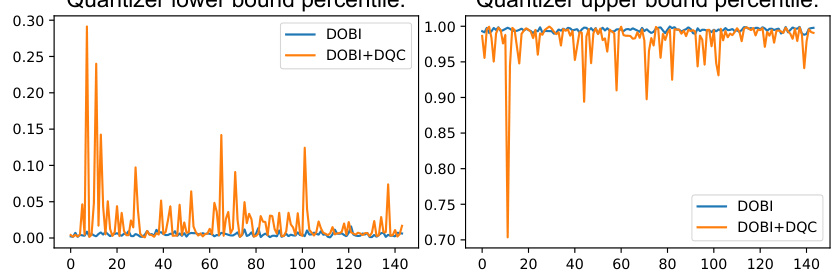
🔼 This figure shows the percentile of the quantizer bounds obtained using the Distribution-Oriented Bound Initialization (DOBI) method and after further fine-tuning with Distillation Quantization Calibration (DQC). The x-axis represents the index of quantizers, and the y-axis represents the percentile. The blue line shows the lower bound percentile from DOBI, while the orange line shows the same after DQC. Similarly, the other lines represent the upper bound percentiles before and after DQC. The figure illustrates how DQC refines the bounds calculated by DOBI, resulting in tighter bounds.
read the caption
Figure 5: The bound percentile of DOBI and DQC.

🔼 This figure shows a visual comparison of the results obtained by different super-resolution (SR) methods on three challenging images from the Urban100 dataset at a scale factor of ×4. The methods compared include Bicubic interpolation, MinMax, Percentile, DBDC+Pac, DOBI, 2DQuant, and the full-precision (FP) SwinIR model. The images highlight the differences in the quality of the reconstructed images and how 2DQuant compares to the state-of-the-art and other quantization methods.
read the caption
Figure 6: Visual comparison for image SR (×4) in some challenging cases.
More on tables
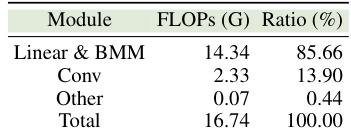
🔼 This table compares the performance and complexity of different super-resolution models. It shows the number of parameters (in MB), the number of floating point operations (in G), and the peak signal-to-noise ratio (PSNR) on the Urban100 dataset for each model. The models compared include EDSR, a 4-bit quantized version of EDSR using the DBDC+Pac method, SwinIR-light, a 4-bit quantized version of SwinIR-light using the DBDC+Pac method, and the proposed 4-bit quantized version of SwinIR-light using the 2DQuant method. The table highlights the efficiency gains achieved by the 2DQuant method in terms of both parameters and FLOPs while maintaining competitive PSNR performance compared to the full-precision models.
read the caption
Table 1: Complexity and performance (×4).

🔼 This table presents a quantitative comparison of the proposed 2DQuant method with state-of-the-art (SOTA) post-training quantization (PTQ) methods for image super-resolution. It shows Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) metrics for different bit depths (2, 3, 4 bits) and upscaling factors (×2, ×3, ×4) on various benchmark datasets (Set5, Set14, B100, Urban100, Manga109). The results highlight 2DQuant’s superior performance, particularly at lower bit depths, compared to existing methods like MinMax, Percentile, EDSR with DBDC+Pac, and DOBI (a component of 2DQuant).
read the caption
Table 3: Quantitative comparison with SOTA methods. EDSR† means applying DBDC+Pac [41] on CNN-based backbone EDSR [34]. Its results are cited from the paper [41].

🔼 This table presents a quantitative comparison of the proposed 2DQuant method with other state-of-the-art (SOTA) post-training quantization (PTQ) methods for image super-resolution. The comparison considers different bit depths (2, 3, and 4 bits) and scaling factors (×2, ×3, and ×4). Metrics used include PSNR and SSIM, evaluated on five benchmark datasets (Set5, Set14, B100, Urban100, and Manga109). The table highlights the superior performance of 2DQuant across various settings, particularly its ability to achieve high PSNR and SSIM values with low-bit quantization.
read the caption
Table 3: Quantitative comparison with SOTA methods. EDSR† means applying DBDC+Pac [41] on CNN-based backbone EDSR [34]. Its results are cited from the paper [41].
Full paper#