↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current data-driven methods for discovering governing differential equations often ignore fundamental physical laws like symmetry, leading to inaccurate or overly complex results. This limits our ability to extract meaningful physical insights from data. The challenge lies in efficiently searching the vast space of possible equations while adhering to known physical principles.
This work introduces a novel approach that integrates symmetry into automated equation discovery. By explicitly incorporating time-independent symmetries, the proposed method significantly reduces the search space and improves the accuracy and parsimony of the discovered equations. This is achieved through a pipeline that adapts various equation discovery algorithms to incorporate symmetry constraints, either by solving them directly or by using them as a regularization term. Experimental results demonstrate superior performance compared to existing methods, especially in noisy datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in dynamical systems and machine learning. It bridges the gap between data-driven equation discovery and fundamental physical laws by incorporating symmetry principles. This advances automated scientific discovery, improves the accuracy and robustness of learned equations, and opens new avenues for research in various fields.
Visual Insights#
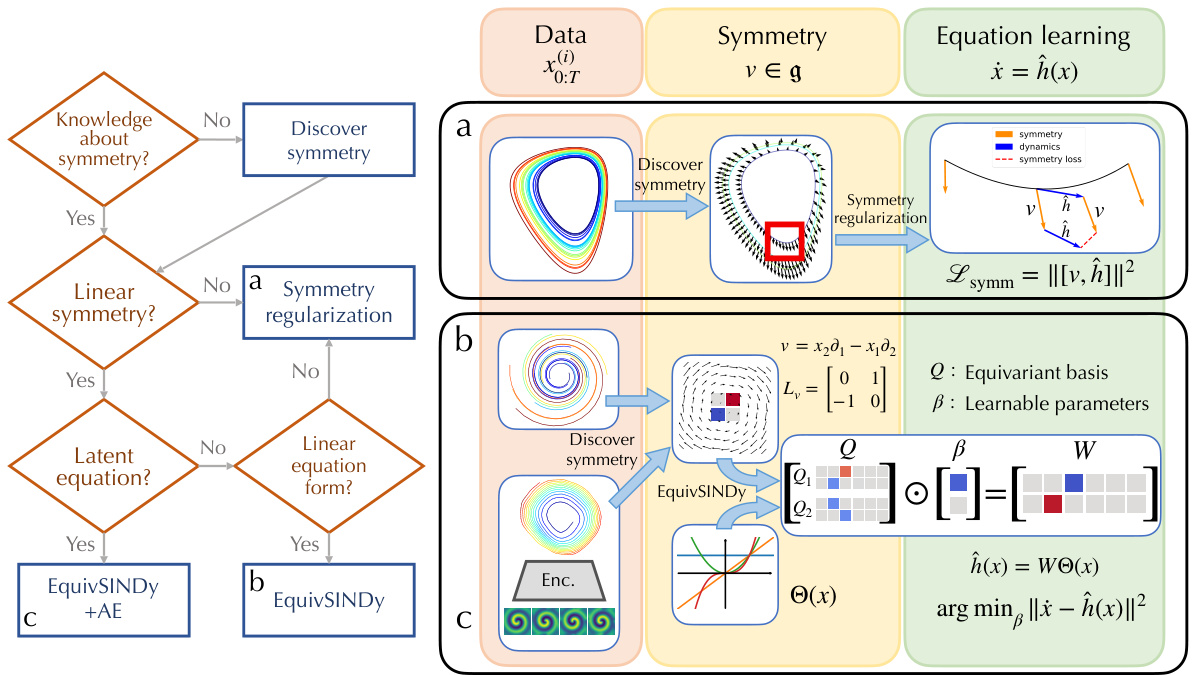
This figure illustrates the pipeline of the proposed symmetry-informed governing equation discovery method. It starts with trajectory data and checks for prior knowledge of symmetries. If symmetries are known, the pipeline branches depending on whether they are linear or not, and whether a latent equation representation is desired. If symmetries are unknown, a symmetry discovery module is employed first. Regardless of the symmetry’s nature, the main equation discovery is then performed, guided or regularized by the identified or learned symmetries. The pipeline is broken down into three sub-pipelines corresponding to solving linear symmetry constraints explicitly, using symmetry regularization, and the case of discovering unknown symmetries from data.

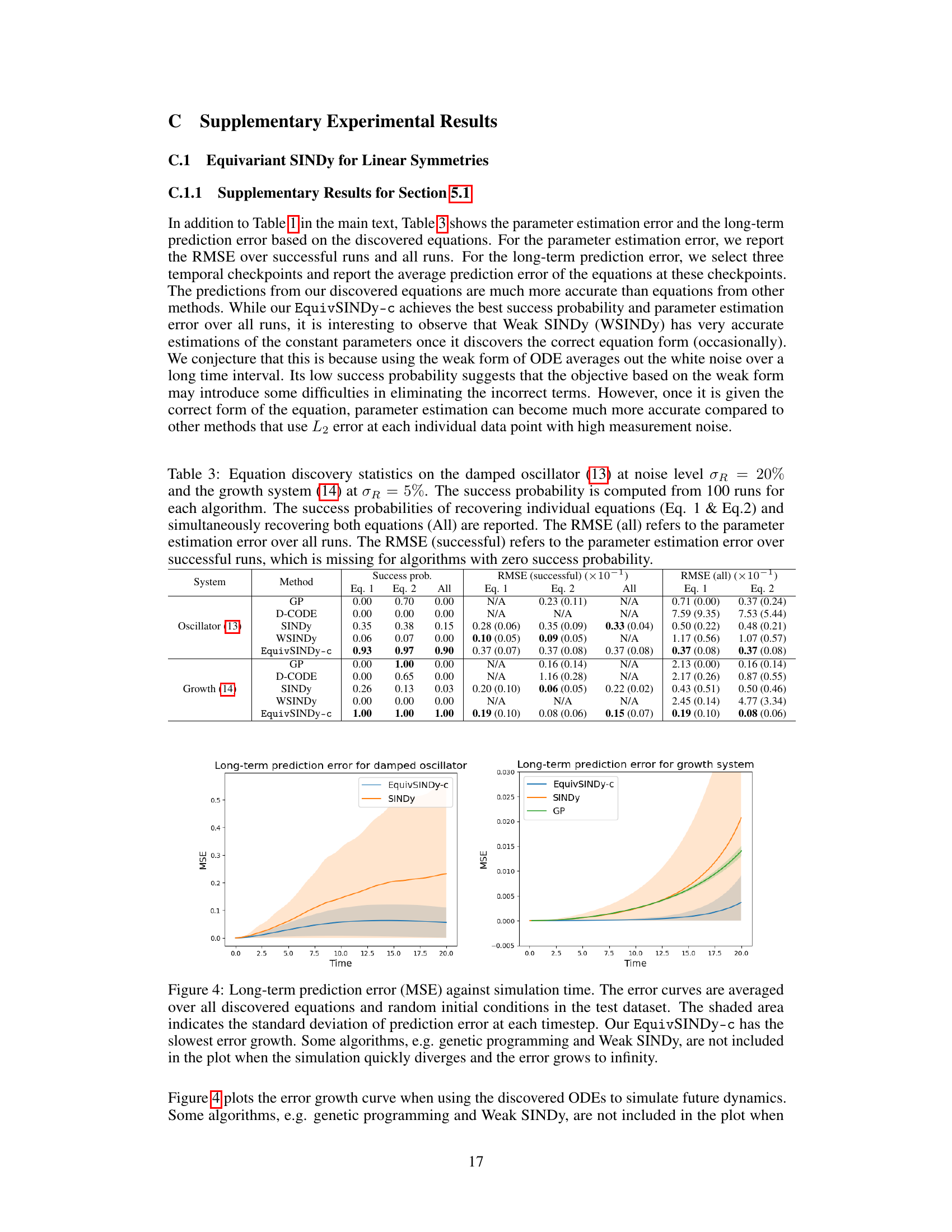
This table presents the success rate of different methods in discovering the correct equations for two dynamical systems: a damped oscillator and a growth system. Each system has two equations. The table shows the success probability for each individual equation (Eq. 1, Eq. 2) and for discovering both equations simultaneously (All). The methods compared include Genetic Programming (GP), D-CODE, SINDY, Weak SINDY (WSINDY), and the proposed EquivSINDy-c. The results highlight the improved performance of EquivSINDy-c which leverages symmetry information.
In-depth insights#
Symmetry in ODEs#
The concept of ‘Symmetry in ODEs’ explores how inherent symmetries within ordinary differential equations (ODEs) can be leveraged to enhance our understanding and analysis. Symmetries, in essence, represent transformations that leave the ODE’s structure unchanged. This understanding is crucial because exploiting these symmetries simplifies the problem, reduces computational costs, and provides deeper insights into the underlying physical processes. The paper likely delves into the theoretical framework of Lie group theory to formally define and characterize these symmetries. A key aspect is the link between time-independent symmetries and the equivariance of the ODE’s flow map. This connection allows researchers to impose constraints during equation discovery, leading to more accurate and parsimonious models. Furthermore, the paper likely discusses techniques to incorporate these symmetry constraints into various equation discovery algorithms, like sparse regression and genetic programming. The presence of noise in real-world data is also addressed, with the paper potentially showing how symmetry considerations can enhance robustness. Finally, the approach’s applicability is demonstrated across diverse dynamical systems, showcasing its generalizability and practical significance. This focus on symmetry is a significant improvement over traditional data-driven methods which often lack awareness of these fundamental physical principles.
Equivariant SINDy#
The concept of “Equivariant SINDy” combines two powerful techniques: Sparse Identification of Nonlinear Dynamics (SINDy), a data-driven method for discovering governing equations, and the principle of equivariance, a crucial concept in physics and machine learning emphasizing symmetry preservation under transformations. This fusion allows SINDy to leverage knowledge of symmetries inherent in the underlying physical system. By incorporating equivariance constraints, the algorithm effectively reduces the search space of possible equations, improving the accuracy, robustness, and simplicity of the discovered models. This is particularly beneficial when dealing with noisy data or high-dimensional systems where traditional SINDy might struggle. The key is to explicitly incorporate the known symmetries into SINDy’s optimization process, leading to more physically meaningful and generalizable models. This approach represents a significant advancement in equation discovery, bridging the gap between data-driven methods and fundamental physical principles.
Symmetry Reg#
The heading ‘Symmetry Reg,’ likely short for ‘Symmetry Regularization,’ points to a crucial technique in the paper for improving the accuracy and robustness of governing equation discovery. This approach leverages the inherent symmetries present in many physical systems. By incorporating symmetry constraints or a symmetry regularization term, the method effectively limits the search space for potential equations. This compression reduces overfitting and the risk of identifying overly complex or less accurate solutions. The effectiveness of this regularization hinges on whether the symmetry is known a priori or needs to be learned from data. For known symmetries, explicit constraint-solving techniques can be employed to dramatically reduce the parameter space. When symmetries are unknown, the paper likely proposes a method to learn them from the data and then uses this learned information to guide the regularization process, improving the algorithm’s robustness to noise. In essence, symmetry regularization acts as a powerful inductive bias, reflecting a fundamental understanding of the underlying physical principles and leading to more physically meaningful and reliable equation discovery.
Higher-Dim Systems#
The section on higher-dimensional systems is crucial because it demonstrates the scalability and robustness of the proposed symmetry-informed methods. It moves beyond the limitations of simpler systems by tackling the challenges of high dimensionality, where traditional methods often struggle. The application to a SEIR epidemic model highlights the practical relevance of the approach, showing how symmetry constraints can significantly improve the accuracy and efficiency of equation discovery. The results showcase the method’s ability to handle complex, real-world scenarios, moving beyond theoretical demonstrations. Addressing high-dimensional data is a significant advance, as it expands the applicability of automated equation discovery to a broader range of scientific and engineering problems. The success in this area suggests a promising path towards more general-purpose tools for scientific modeling from data. Further investigation into the types of symmetries that are most effective in high-dimensional spaces and how to learn these symmetries efficiently from limited data would be very valuable.
Future Works#
Future research directions stemming from this symmetry-informed governing equation discovery work could focus on extending the approach to time-dependent symmetries and non-autonomous ODEs, which are more complex. Investigating the effectiveness of the methodology on partial differential equations (PDEs) would also be valuable, requiring adaptation of the symmetry constraints to higher dimensional systems. A key challenge is automatically discovering symmetries from data when no prior knowledge exists, and this could be tackled by improving existing symmetry discovery methods. Furthermore, exploring the use of different types of symmetries beyond Lie point symmetries, and examining the application to different equation discovery algorithms beyond those studied in the paper, would offer broader applicability and insights. Finally, a rigorous theoretical understanding of how symmetry regularization impacts the ability to discover parsimonious and accurate equations warrants further investigation.
More visual insights#
More on figures
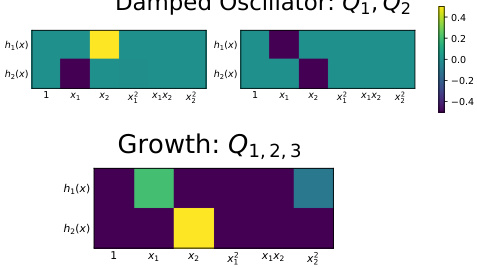
This figure visualizes the parameter spaces for two dynamical systems (Damped Oscillator and Growth) under the equivariance constraint. The original parameter space is reduced significantly due to the constraint. For the damped oscillator, the 2D parameter space is spanned by Q1 and Q2. For the Growth system, the 3D parameter space is spanned by Q1, Q2, and Q3, each represented by a different color. This demonstrates the effect of incorporating symmetry constraints into reducing the search space for equation discovery.

This figure shows a reaction-diffusion system and compares the prediction errors of three different methods: EquivSINDYAE, LaLiGAN + SINDY, and SINDYAE. The left panel displays a visualization of the reaction-diffusion system. The right panel presents a line graph plotting the mean squared error (MSE) against the timestep for each method. Shaded areas represent standard deviations across three runs. The graph visually demonstrates the superior performance of EquivSINDYAE in accurately predicting the system’s dynamics over time, particularly compared to SINDYAE which exhibits significantly larger and more unstable errors.

This figure shows the pipeline of incorporating symmetries into equation discovery. The pipeline starts with trajectory data from a dynamical system. Based on prior knowledge or via a symmetry discovery technique, the system’s symmetry is identified. Then, depending on whether the symmetry is linear, the pipeline uses one of two methods: 1) solving a set of constraints to enforce the symmetry; or 2) promoting symmetry through regularization. The outcome is a symmetry-informed governing equation.

This figure shows the pipeline of incorporating symmetries into equation discovery algorithms. It starts with trajectory data and determines if prior knowledge about symmetry exists. If not, the pipeline uses symmetry discovery techniques. Then, it checks for linear symmetry; if present, it solves the linear symmetry constraints. Otherwise, it uses symmetry regularization. The final output is the learned governing equation.
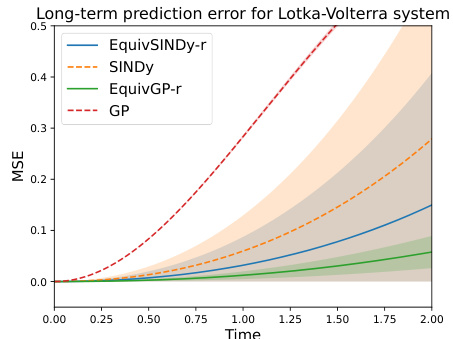
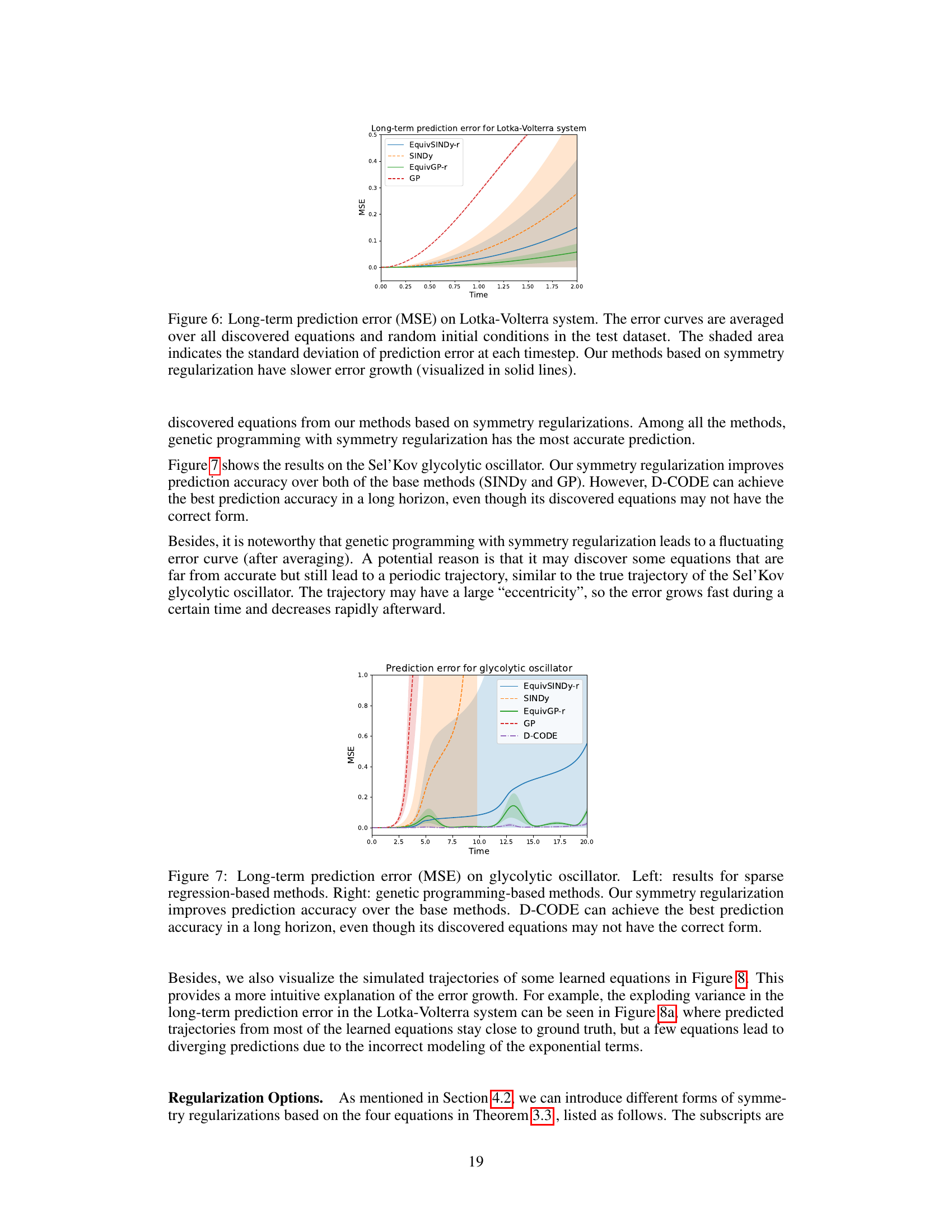
This figure shows the long-term prediction error for the Lotka-Volterra system using different methods. The y-axis represents the mean squared error (MSE), and the x-axis represents the simulation time. The solid lines represent the methods using symmetry regularization, and the dashed lines represent the baseline methods. The shaded area represents the standard deviation. The figure demonstrates that the methods incorporating symmetry regularization have slower error growth compared to the baseline methods.
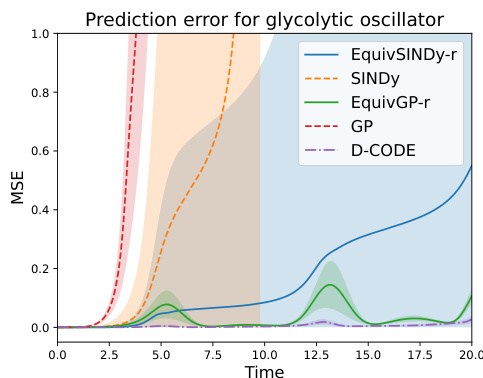
This figure compares the long-term prediction error (Mean Squared Error or MSE) of different methods for the glycolytic oscillator model. It shows that incorporating symmetry regularization via the proposed EquivSINDy-r and EquivGP-r methods leads to lower prediction errors compared to standard SINDy and GP methods, particularly over longer prediction horizons. While D-CODE achieves the lowest error, its discovered equations may not always correctly capture the model dynamics.
This figure shows the pipeline for incorporating symmetries into equation discovery. It starts with trajectory data and determines if prior knowledge of symmetry exists. If yes, it leverages that to solve linear symmetry constraints or use symmetry regularization. If not, symmetry discovery techniques are applied to first learn the symmetry before enforcing it via constraints or regularization. The pipeline branches according to whether the symmetry is linear, solvable or requires regularization, leading to different methods for equation discovery.

This figure shows the pipeline of the proposed symmetry-informed governing equation discovery method. It details the steps involved in leveraging symmetry knowledge (either known beforehand or learned from data) to enhance equation discovery algorithms. The pipeline branches based on whether the symmetry is linear and explicitly solvable, or requires regularization techniques. This approach aims to improve accuracy and parsimony in the discovered equations.
More on tables

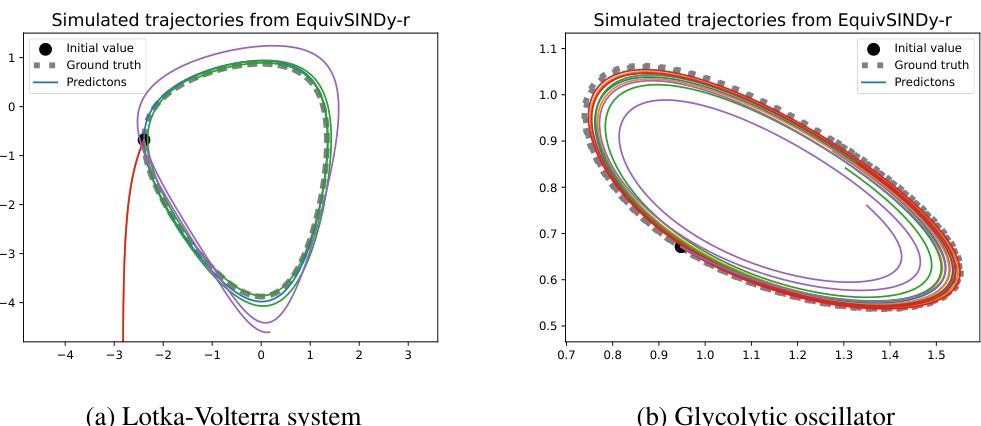
This table presents the performance of different equation discovery methods (SINDy, WSINDy, EquivSINDy-r, GP, D-CODE, EquivGP-r) on two benchmark systems: the Lotka-Volterra and the glycolytic oscillator. The results show success probabilities for discovering individual equations and both equations simultaneously, along with RMSE (root mean square error) values for parameter estimation (both overall and for successful runs only). The RMSE values are scaled differently for the two systems.
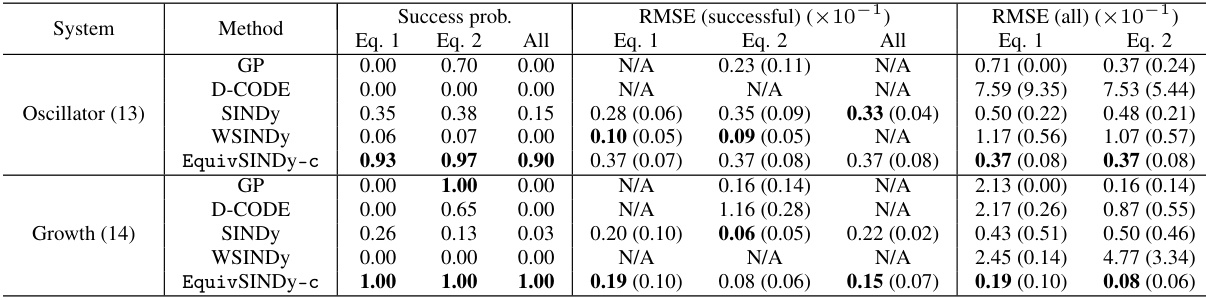
This table presents the results of equation discovery experiments on two systems: the damped oscillator and the growth system. It shows the success rate of different algorithms in recovering the correct equation, along with parameter estimation errors (RMSE). The RMSE is reported for all runs and only for successful runs.

This table presents the results of equation discovery experiments on a 4-dimensional SEIR epidemic model using SINDy and EquivSINDy-c methods. The success probabilities of recovering individual equations (Eq. 1 & Eq. 2) and simultaneously recovering both equations (All) are reported, along with RMSE (successful) and RMSE (all). The RMSE (all) is the parameter estimation error averaged over all runs. The RMSE (successful) is the parameter estimation error averaged only over successful runs.

This table presents the results of equation discovery experiments on two systems: the damped oscillator and the growth system. It compares several methods, showing success rates (probability of finding the correct equation form), parameter estimation error considering all runs and only successful runs. The table highlights the impact of incorporating symmetry constraints in improving accuracy and robustness.
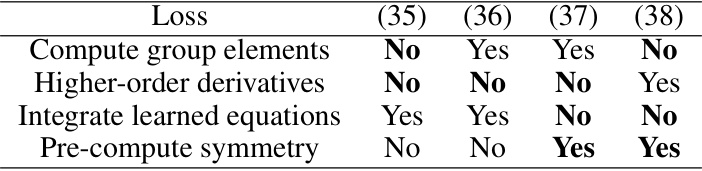
This table compares four different symmetry regularization loss functions (equations 35, 36, 37, and 38 from the paper) based on their computational requirements. It details whether each loss requires computation of group elements, higher-order derivatives, integration of learned equations, and pre-computation of symmetries. This helps readers understand the trade-offs associated with each loss function when applied to various equation discovery algorithms.

This table compares the latent equations discovered by three different methods: SINDyAE, LaLiGAN+SINDy, and EquivSINDyAE. Each method provides samples of the discovered equations. The equations describe the dynamics in the latent space of a reaction-diffusion system. Note that there is no single correct answer for the latent equations, because there might exist different latent spaces where the high-dimensional dynamics can be described accurately via different equations. Thus, the analysis in this subsection is mainly qualitative.
Full paper#