↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Deep Generative Models (DGMs) are increasingly used to create synthetic data for privacy-preserving research. However, analyses on this synthetic data often suffer from substantial bias and imprecision, slowing down convergence rates and compromising the reliability of results. This undermines the inferential utility of synthetic data significantly and calls for innovative solutions.
This study introduces a novel, generator-agnostic debiasing strategy that targets synthetic data generated by DGMs. The method is based on insights from debiased and targeted machine learning, accounting for biases and enhancing convergence rates. The study validates the approach via simulation and real-world data analysis on two datasets, demonstrating improved accuracy and reliability of statistical estimations from the debiased synthetic data.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with synthetic data, especially those using deep generative models. It directly addresses the pervasive issue of bias in synthetic data analysis, offering a novel and practical solution to improve the reliability and validity of research findings. This opens avenues for more trustworthy AI applications across various domains.
Visual Insights#
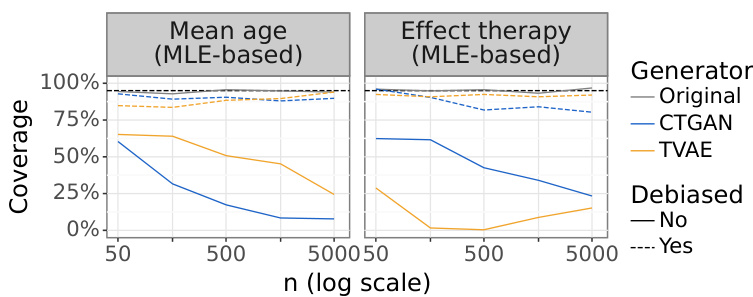
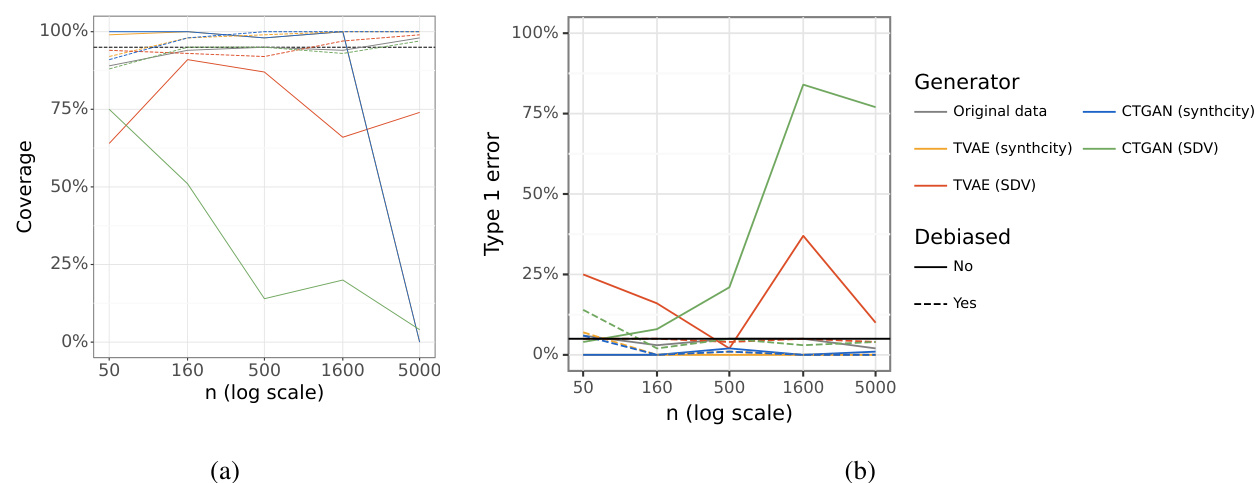
This figure displays the empirical coverage of 95% confidence intervals for two different population parameters: the mean age and the effect of therapy on blood pressure (adjusted for stage). The results are shown for original data and data generated using two different deep generative models (CTGAN and TVAE), both with and without the proposed debiasing strategy. The x-axis represents sample size (n, on a logarithmic scale), and the y-axis represents the empirical coverage (percentage). The figure demonstrates the impact of the debiasing strategy on improving coverage, especially at larger sample sizes.

This table presents the estimated exponent α and its 95% confidence interval for the convergence rate n−α of the empirical standard error (SE) for the population mean of age and the effect of therapy on blood pressure adjusted for stage. The values are obtained for different deep generative models (CTGAN and TVAE) using both default and debiased synthetic datasets. The exponent α indicates how quickly the SE shrinks with increasing sample size (n). A value of 0.5 represents the typical 1/√n rate of convergence expected for unbiased estimators. Deviations from 0.5 suggest slower or faster convergence.
In-depth insights#
DGM Bias Issue#
The core issue lies in the inherent biases introduced by Deep Generative Models (DGMs) during synthetic data creation. DGMs, while powerful, aren’t perfect estimators of the true data distribution. They learn complex patterns and relationships, but these learned patterns might not perfectly reflect all aspects of the original data, leading to systematic biases in the generated synthetic data. This is particularly problematic for statistical inference, where even seemingly minor biases can significantly affect estimates of population parameters and measures of uncertainty like confidence intervals or p-values. The bias often manifests as slower-than-expected convergence rates in downstream statistical analyses, meaning that larger sample sizes are needed to achieve the same level of precision as with real data. Addressing this bias effectively requires a careful strategy that accounts for the limitations of DGMs and aims to correct or mitigate the distortions introduced during the synthesis process. Tailoring DGMs for targeted data analyses and employing debiased estimation techniques, as explored in the paper, are crucial steps in alleviating this significant challenge.
Debiasing Strategy#
The core of the paper centers around a novel debiasing strategy designed to address the inherent biases introduced when using deep generative models (DGMs) to create synthetic datasets. The strategy directly tackles the slow convergence rates often observed in analyses of DGM-generated data, a major obstacle to reliable statistical inference. Instead of relying on multiple synthetic datasets or complex data-adaptive procedures, this approach focuses on tailoring the DGM for specific analyses, leveraging insights from debiased and targeted machine learning. By directly addressing biases, the strategy improves convergence rates, enabling more accurate estimation and the efficient calculation of large-sample variances. The method is generator-agnostic, making it adaptable to various DGMs, and its effectiveness is demonstrated through simulations and real-world case studies, showcasing its ability to improve the reliability and applicability of synthetic data in statistical inference. The key innovation lies in a targeted post-processing step to ensure both generator and analysis bias is mitigated, which directly contributes to advancing the trustworthiness of synthetic data analyses.
Simulation Study#
A simulation study is crucial for validating a novel debiasing strategy for synthetic data generated by deep generative models. It allows researchers to control the data-generating process, enabling precise calculation of bias and convergence rates for estimators, both with and without the debiasing method applied. The study should cover multiple scenarios, varying sample sizes and potentially exploring different deep generative models to evaluate the strategy’s robustness and generality. The study should also incorporate a comparison of standard confidence intervals from synthetic data before and after debiasing, demonstrating the improvement in coverage and uncertainty estimation. Key metrics to assess include bias, standard error, coverage of confidence intervals and convergence rates. Analyzing these metrics will provide strong empirical evidence supporting the effectiveness and limitations of the proposed debiasing approach. A well-designed simulation study is essential for establishing the credibility and practical impact of the proposed method.
Real-World Tests#
A dedicated ‘Real-World Tests’ section would significantly strengthen a research paper on synthetic data. It should showcase the practical applicability and limitations of the proposed debiasing method. Multiple case studies, ideally across diverse domains and data types (e.g., healthcare, finance, social sciences), are needed. Each study should thoroughly describe the data source, pre-processing steps, DGM training and evaluation metrics, emphasizing the improvements in accuracy and bias reduction achieved with the proposed debiasing strategy compared to standard methods. Crucially, the section should quantify the gains in inferential utility, perhaps through comparison of confidence interval coverage, p-values, or other relevant statistical measures. Addressing potential challenges encountered in real-world applications, like missing data handling, high-dimensionality, or variable type mismatches, is key. The discussion should also openly acknowledge limitations, such as the computational cost or the dependence on access to the original dataset for debiasing. Focus on practical implications, illustrating how the method enhances the reliability and trustworthiness of analyses using synthetic data in real-world scenarios, thus increasing user confidence and adoption.
Future Research#
Future research directions stemming from this work on debiased synthetic data generation could explore several key areas. Extending the methodology to high-dimensional data and complex models is crucial, as current results are primarily demonstrated on low-dimensional data. This involves investigating the theoretical properties and empirical performance under more realistic, higher-dimensional settings. Developing efficient sample splitting techniques is important to mitigate bias from data-adaptive methods, particularly for complex models. While sample splitting was mentioned in the paper, efficient implementations that balance bias reduction with efficiency gains need further research. Addressing the limitations imposed by the use of conditional sampling for the regression coefficients could also involve the exploration of alternative strategies. Finally, applying the methodology to a broader range of generative models and analyses beyond the specific ones considered is essential to establish the generality and robustness of the proposed approach. These extensions would solidify the practical impact and reliability of debiased synthetic data for real-world statistical inference.
More visual insights#
More on figures

The figure shows the results of the simulation study in terms of bias and standard error. Figure 3a shows the estimates of the population mean of age per Monte Carlo run. Each point represents an estimate, and the funnel represents the behavior of an unbiased and square-root-n-consistent estimator based on observed data. Figure 3b displays the empirical and average MLE-based standard error for the sample mean of age.

This figure displays the empirical coverage of the 95% confidence intervals for the risk difference in death between the treatment arms (aspirin and no aspirin) based on original data, default synthetic data, and debiased synthetic data for the International Stroke Trial (IST) dataset. Each point represents the result of a single Monte Carlo simulation run (n=500). The horizontal dashed line represents the true risk difference from the population (-0.009). The funnel represents the typical behavior of an unbiased, root-n consistent estimator based on observed data. The figure shows that using default synthetic data leads to confidence intervals that frequently do not contain the true risk difference. The debiased synthetic data considerably improves the coverage.
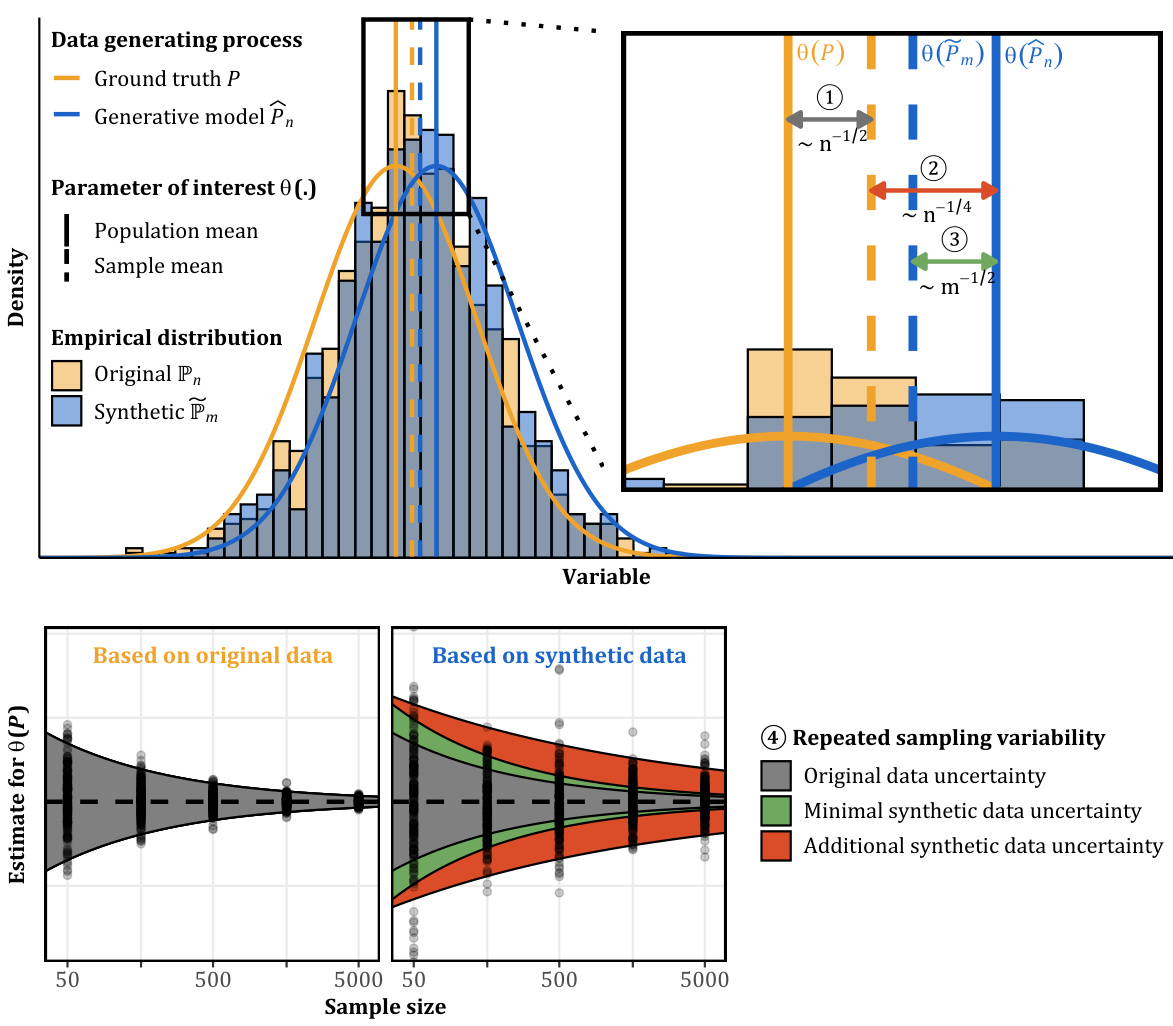
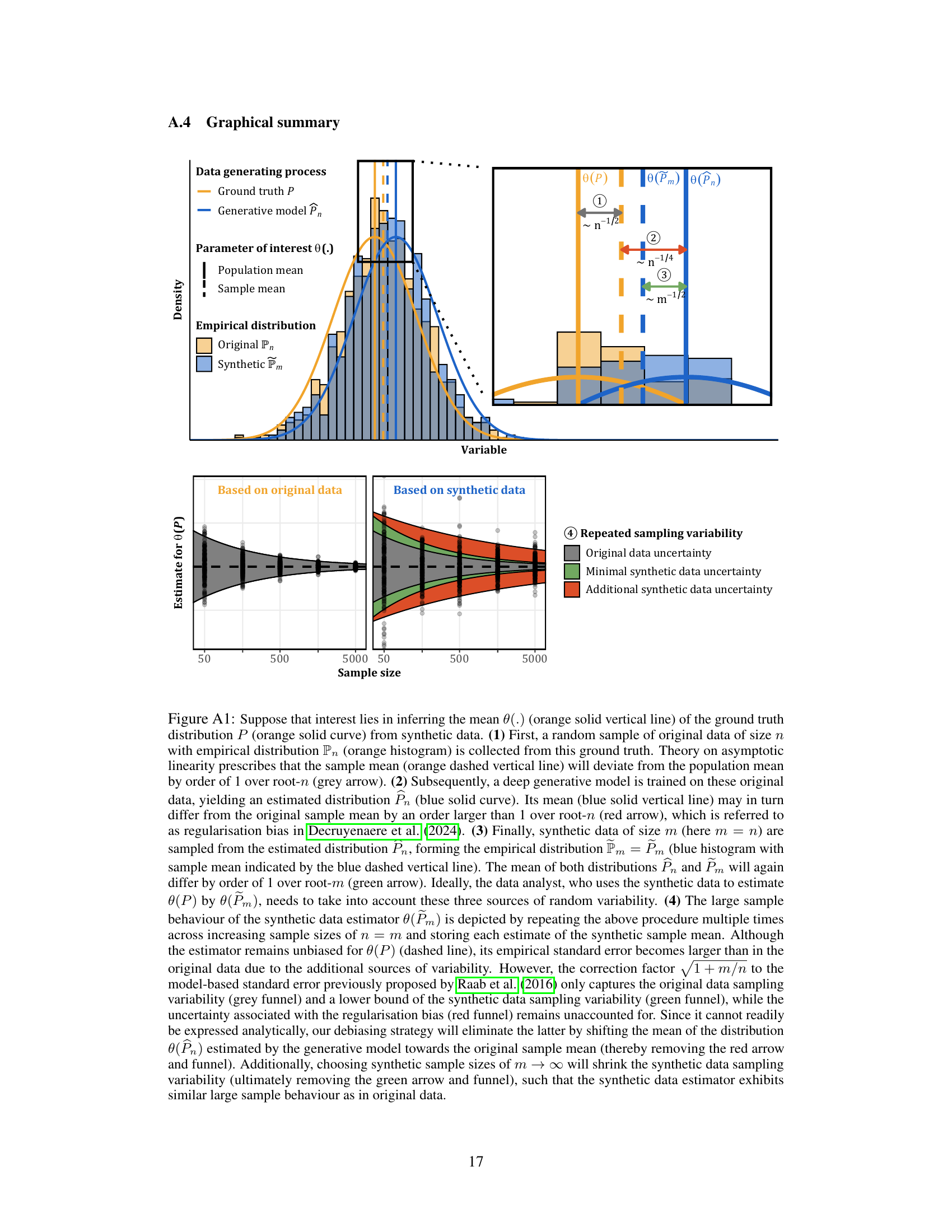
This figure illustrates the three sources of uncertainty when using synthetic data generated by a deep generative model to estimate a population parameter. It shows how the sample mean from original data, the estimated mean from a trained generative model, and the sample mean from synthetic data generated by that model will all differ from the true population parameter. The figure also highlights how a correction factor and debiasing strategy can help mitigate the uncertainty and improve the accuracy of the estimate using synthetic data.

This figure displays the empirical coverage of 95% confidence intervals for two different population parameters: the mean of age and the effect of therapy on blood pressure (adjusted for stage). The coverage is shown for different sample sizes (n) and for both original data and data generated by two different deep generative models (CTGAN and TVAE). It also distinguishes between results with and without the application of the debiasing strategy proposed in the paper. The results show how the debiasing strategy improves the coverage of the confidence intervals, bringing them closer to the nominal level (95%). The figure shows that without the debiasing strategy the coverage decreases as the sample size increases for both CTGAN and TVAE because the standard error shrinks slower than the typical rate of 1/√n.
The figure shows the results of the simulation study on the sample mean of age. Figure 3a shows the estimates for the population mean of age, and Figure 3b shows the empirical and average MLE-based standard errors for the sample mean of age. The funnel in Figure 3a indicates the behaviour of an unbiased and √n-consistent estimator based on observed data. The results show how the debiasing strategy affects the bias, variability, and convergence rate of the estimator.

The figure displays the empirical and MLE-based standard errors for the sample mean of age across different sample sizes (n) and for different deep generative models (CTGAN and TVAE). Each point represents an average over multiple Monte Carlo simulations. The MLE-based standard errors, calculated under the assumption of a root-n consistent estimator, are compared to the empirical standard errors. Debiasing has a significant positive effect on the empirical standard errors’ convergence rate and their approximation by the MLE-based SE.

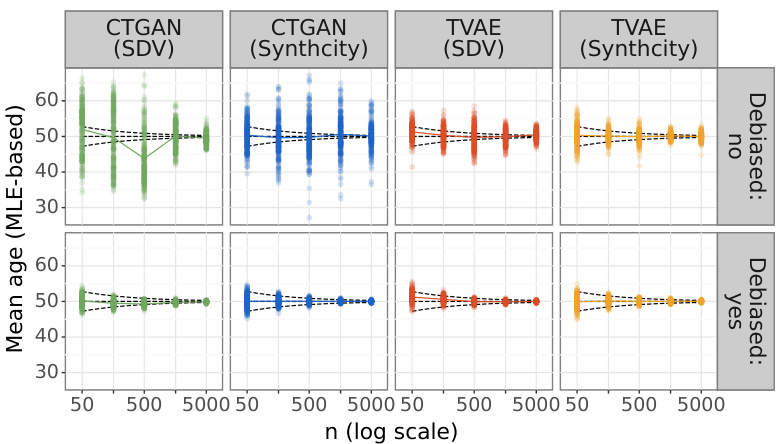
This figure shows the empirical coverage of 95% confidence intervals for MLE-based estimators of the population mean of age and the population effect of therapy on blood pressure, adjusted for stage. It compares the coverage obtained from original data, default synthetic datasets (generated using CTGAN and TVAE with hyperparameters from SDV and Synthcity), and debiased synthetic datasets. The results illustrate the impact of debiasing on coverage, showing that debiasing improves coverage, particularly for the population mean, while coverage for the effect of therapy remains closer to the nominal level (95%) only at larger sample sizes.
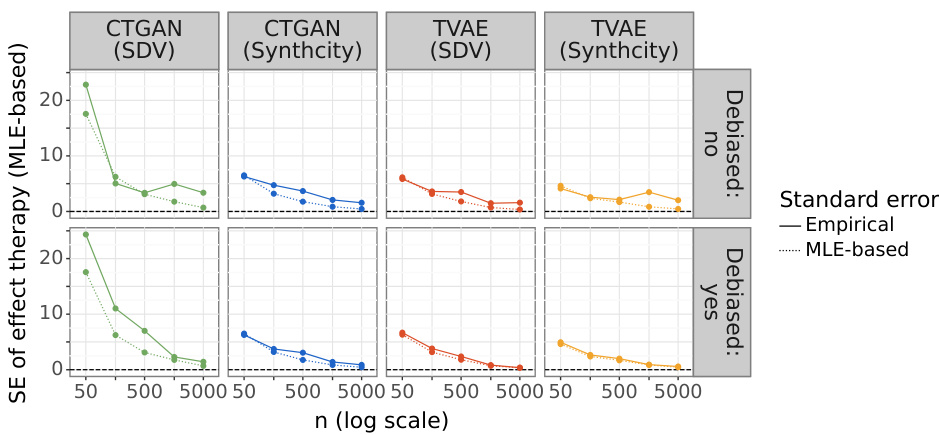
The figure shows the empirical and MLE-based standard errors for the effect of therapy on blood pressure, adjusted for stage. It visually demonstrates how the standard error of the maximum likelihood estimate (MLE) underestimates the empirical standard error, especially in smaller sample sizes. The data is split into four panels based on the deep generative model used (CTGAN(SDV), CTGAN(Synthcity), TVAE(SDV), TVAE(Synthcity)) and whether debiasing was applied. This shows how debiasing improves the approximation of the MLE standard error to the empirical standard error.
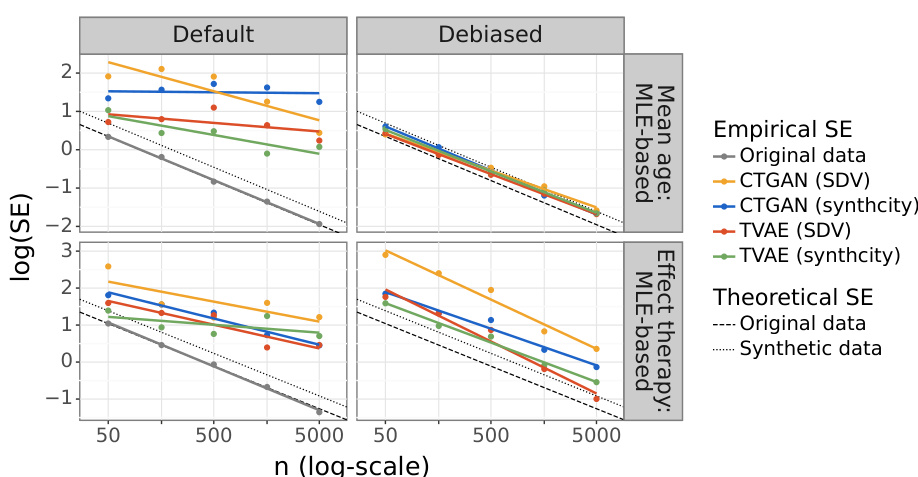
This figure displays the convergence rate of the empirical standard error (SE) for the maximum likelihood estimation (MLE)-based estimators. The slope of the lines show the convergence rate (n⁻ª), where a is estimated. A slope of -0.5 indicates a convergence rate of 1/√n, as expected for an unbiased and consistent estimator with original data. The plot compares the convergence rates of the MLE-based SE for original data and synthetic data generated by different deep generative models, both before and after the proposed debiasing strategy. It illustrates how the debiasing strategy improves convergence to the expected 1/√n rate.

This figure displays the empirical coverage of the 95% confidence intervals for both MLE-based and EIC-based estimators for the population mean of age and the population effect of therapy on blood pressure adjusted for stage. The results are shown for original data and synthetic data generated using CTGAN and TVAE with and without the proposed debiasing strategy. The figure helps visualize how the debiasing strategy improves the coverage, especially for smaller sample sizes and when using synthetic data.

This figure displays the MLE-based and EIC-based estimates of the population mean of age and the effect of therapy on blood pressure adjusted for stage, across different sample sizes (n). The horizontal dashed line represents the true population parameter value. Each dot shows an estimate from a single Monte Carlo simulation run. The funnel illustrates the expected behavior of an unbiased and consistent estimator from observed data, demonstrating how the standard error should shrink with increasing sample size. The figure compares the estimates from original data, default synthetic data, and debiased synthetic data, to illustrate the effect of the debiasing strategy on reducing bias and variance in synthetic data.

The figure shows the convergence rate of the empirical standard error for both MLE-based and EIC-based estimators. The slope of the lines indicates the convergence rate, while the vertical offset represents the log asymptotic variance. Dashed and dotted lines show the expected behavior for estimators based on real and synthetic data respectively. The figure helps to illustrate how the debiasing strategy affects the convergence rate and variance of the estimators.
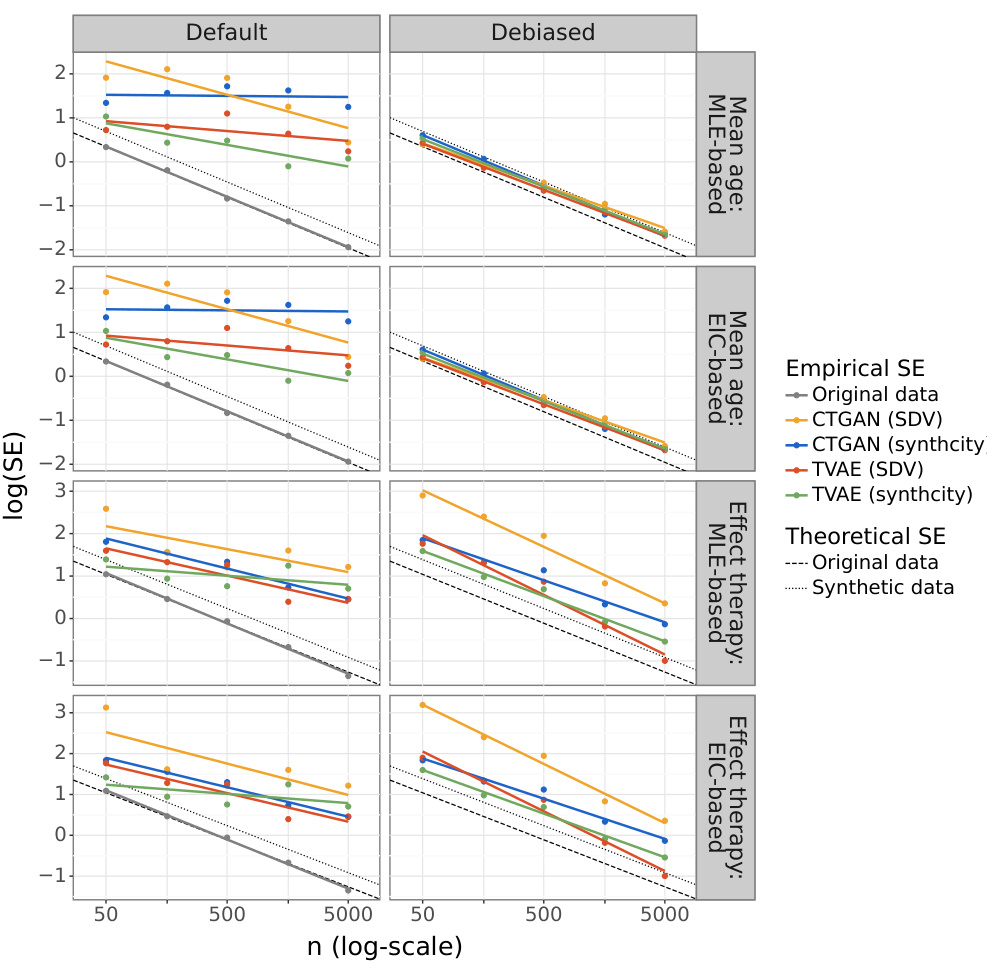
This figure shows the convergence rate of the empirical standard error for the MLE-based estimators. The slope of the lines indicates the convergence rate, and the vertical intercept indicates the asymptotic variance. The dashed line represents the expected behavior for an unbiased, root-n consistent estimator based on real data. The dotted line shows the expected behavior for a similar estimator based on synthetic data using a correction factor from Raab et al. (2016). Parallel lines to the dashed and dotted lines indicate root-n convergence, while horizontal or vertical lines indicate slower or faster convergence, respectively.
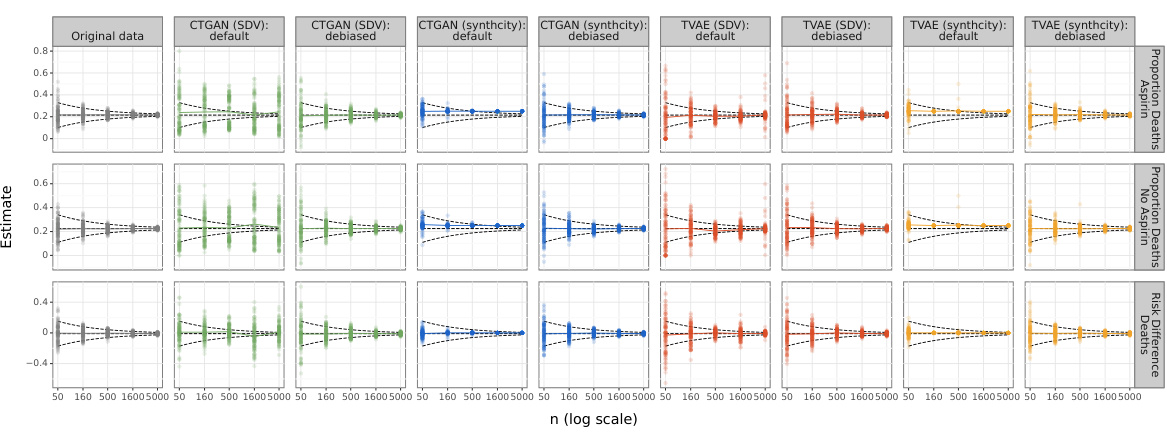
This figure shows the results for the proportion of deaths in the aspirin and no-aspirin groups, as well as their risk difference, for both default and debiased synthetic data. It compares the results across four different generative models (CTGAN (SDV), CTGAN (Synthcity), TVAE (SDV), and TVAE (Synthcity)) and varying sample sizes (n). The horizontal dashed line indicates the true population values, providing a visual comparison of the estimates’ accuracy and precision. The funnel represents the expected behavior of an unbiased estimator with a convergence rate of 1/√n, illustrating how the estimates’ variability decreases as the sample size increases.
This figure shows the empirical coverage and type 1 error rate for the proportion of death in the aspirin treatment arm and the risk difference in death between aspirin and no aspirin groups, based on original, default, and debiased synthetic data. The results indicate that the debiasing strategy improves the coverage and reduces type 1 error, especially for smaller sample sizes.
More on tables
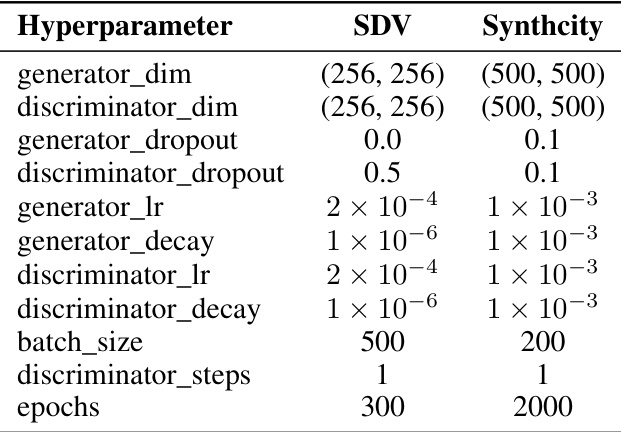
This table compares the default hyperparameters used for training the CTGAN model in two different software packages: SDV and Synthcity. It highlights the differences in the settings for various parameters such as generator and discriminator dimensions, dropout rates, learning rates, decay rates, batch size, discriminator steps, and training epochs. These differences can lead to variations in the performance and characteristics of the generated synthetic data.
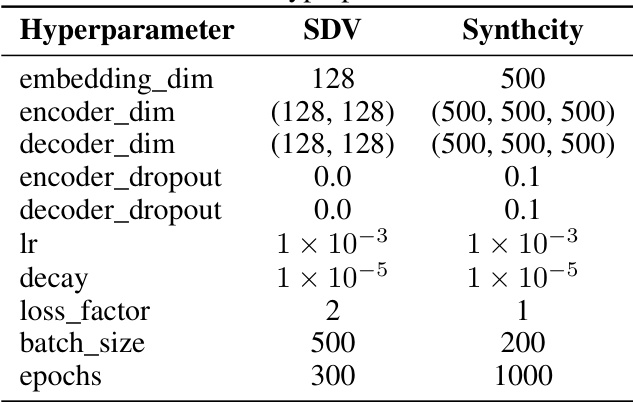
This table compares the default hyperparameter settings for the TVAE model between two different software packages, SDV and Synthcity. It lists the values for various hyperparameters, such as embedding dimension, encoder and decoder dimensions, dropout rates, learning rate, decay rate, loss factor, batch size, and number of epochs. These hyperparameters influence the training process and ultimately the performance of the TVAE model in generating synthetic data.

This table displays the Inverse Kullback-Leibler Divergence (IKLD) between the original and synthetic datasets generated by four different deep generative models (DGMs) under two different sets of hyperparameters, for five different sample sizes. The IKLD is a measure of similarity between probability distributions, with higher values indicating greater similarity. The table shows the IKLD for both default and debiased synthetic datasets, allowing for a comparison of the impact of the debiasing strategy on data quality.
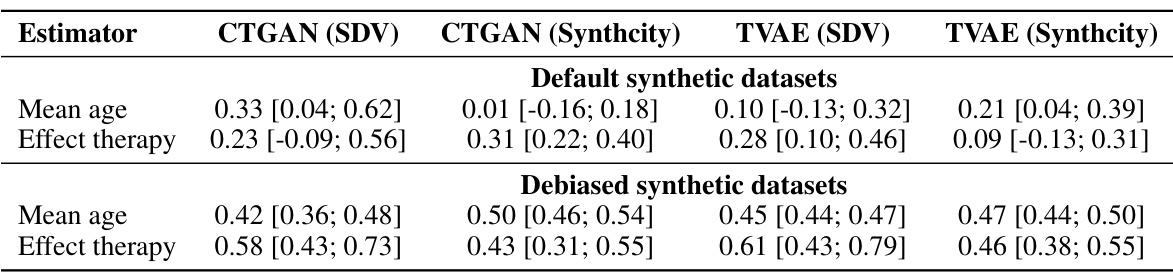
This table presents the estimated exponent α (along with its 95% confidence interval) for the power-law convergence rate n⁻ª of the empirical standard error (SE) for the estimators used in the simulation study. The exponent α quantifies how quickly the SE shrinks as the sample size (n) increases. A value of α close to 0.5 indicates a typical 1/√n convergence rate, while values significantly lower than 0.5 indicate slower than expected convergence. The table shows these estimates for both default and debiased synthetic datasets generated using two different deep generative models (CTGAN and TVAE), for both mean age and effect therapy estimators. This information is crucial to understand how the accuracy and precision of the estimations change with sample size.

This table presents the estimated exponent and its 95% confidence interval for the power law convergence rate (n-a) of the difference between functionals of Pm and Pn in L2(Pn). The functionals considered are conditional expectations of the exposure (A) and outcome (Y) given different values of the covariate (X). The table shows results for four different deep generative models: CTGAN (SDV), CTGAN (Synthcity), TVAE (SDV), and TVAE (Synthcity). The values in the table are the estimated exponents of the power law. A value closer to 0.5 would indicate root-n convergence for the given functional. The confidence intervals provide a measure of uncertainty in the estimate.
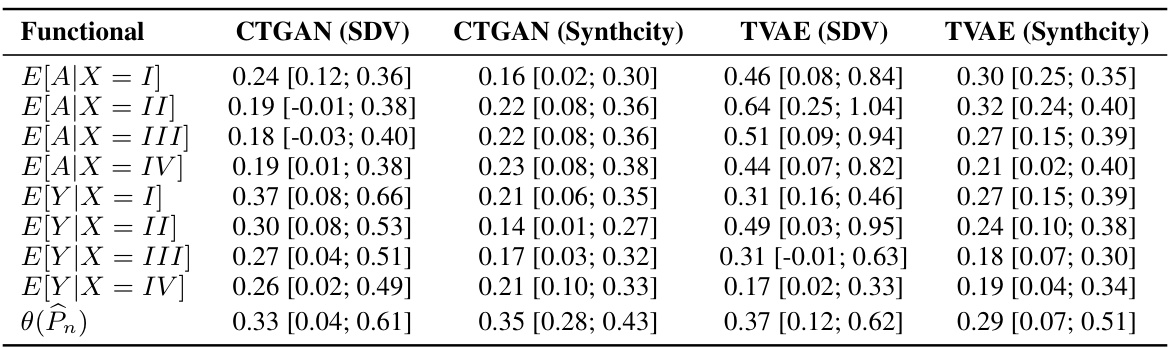
This table presents the estimated exponent α and its 95% confidence interval for the power law convergence rate n-α. The convergence rate describes how quickly the difference between functionals of the estimated distribution Pn (from the DGM) and the true distribution P shrinks as the sample size n increases. The functionals considered are conditional expectations of exposure A and outcome Y given different values of covariate X, along with the estimated regression coefficient θ(Pn). The results are shown separately for CTGAN (SDV), CTGAN (Synthcity), TVAE (SDV), and TVAE (Synthcity).

This table summarizes the findings of the simulation study regarding the effect of the proposed debiasing strategy on the bias, standard error (SE), and coverage of confidence intervals for two estimators: the mean age and the effect of therapy on blood pressure. The results are shown for different deep generative models (DGMs) with and without the debiasing applied. It illustrates the impact of the debiasing strategy on the bias, SE, and coverage, highlighting its effectiveness in achieving more accurate and reliable estimates.
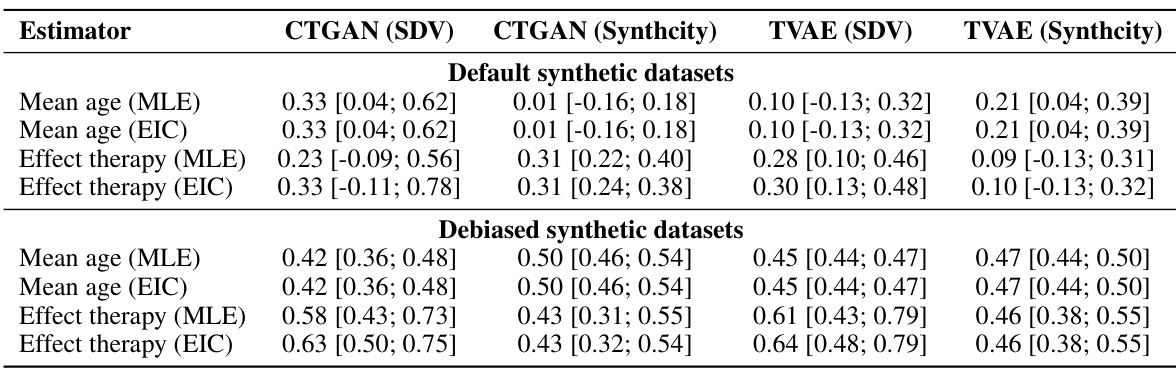
This table presents the estimated exponents and their 95% confidence intervals for the power law convergence rate (n⁻ª) of the empirical standard errors (SEs) for different estimators and models (CTGAN (SDV), CTGAN (Synthcity), TVAE (SDV), TVAE (Synthcity)). The exponents represent how quickly the SEs decrease with increasing sample size (n). An exponent of 0.5 indicates the typical √n convergence rate. Values less than 0.5 indicate slower than typical shrinkage, and values greater than 0.5 indicate faster shrinkage. The table shows the results for both default and debiased synthetic datasets, highlighting the impact of the debiasing strategy on the convergence rate of SEs.

This table presents the estimated exponent and its 95% confidence interval for the power law convergence rate (n-a) of the empirical standard error (SE) for different estimators (proportion death aspirin group, proportion death no aspirin group, and risk difference death) and for different data generation methods (original, CTGAN(SDV), CTGAN(Synthcity), TVAE(SDV), TVAE(Synthcity)). It shows results for both default and debiased synthetic datasets. The NaN values indicate that the convergence rate could not be estimated due to lack of variance in the estimates for certain sample sizes and methods.
Full paper#