↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Simple bilevel optimization problems involve minimizing an upper-level objective function while satisfying the optimal solution of a lower-level problem. These problems pose significant challenges due to their complex feasible set. Existing methods often struggle with slow convergence or stringent assumptions. This research focuses on addressing these challenges and improving the efficiency of solving simple bilevel optimization problems.
The paper introduces AGM-BiO, a novel method employing a cutting-plane approach to locally approximate the lower-level solution set. AGM-BiO utilizes an accelerated gradient-based update to efficiently minimize the upper-level objective function. The authors provide theoretical guarantees showing that their method achieves optimal or near-optimal convergence rates, especially when dealing with the additional assumption of compact feasible sets or the r-th order Hölderian error bound condition on the lower-level objective. Their empirical results confirm the superior performance of AGM-BiO compared to state-of-the-art techniques.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in bilevel optimization and related fields because it presents a novel algorithm (AGM-BiO) with improved convergence guarantees compared to existing methods. Its superior efficiency, particularly when dealing with composite or Hölderian error bound conditions, makes it a valuable tool for tackling complex real-world problems. The research opens avenues for further investigation into non-asymptotic analysis of bilevel optimization, particularly for higher-order Hölderian error bound scenarios.
Visual Insights#
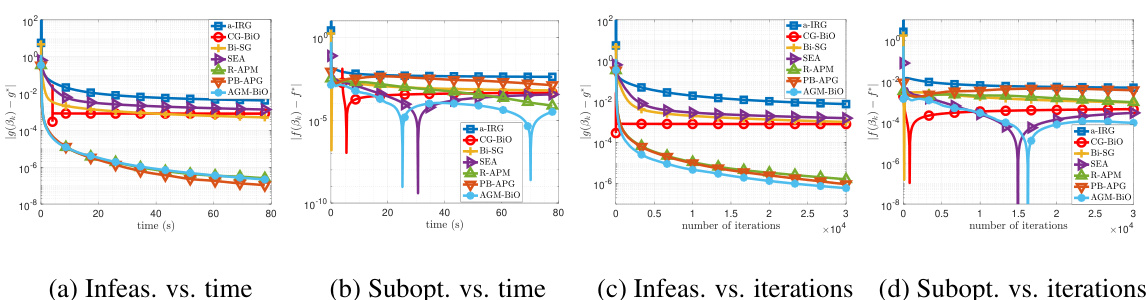
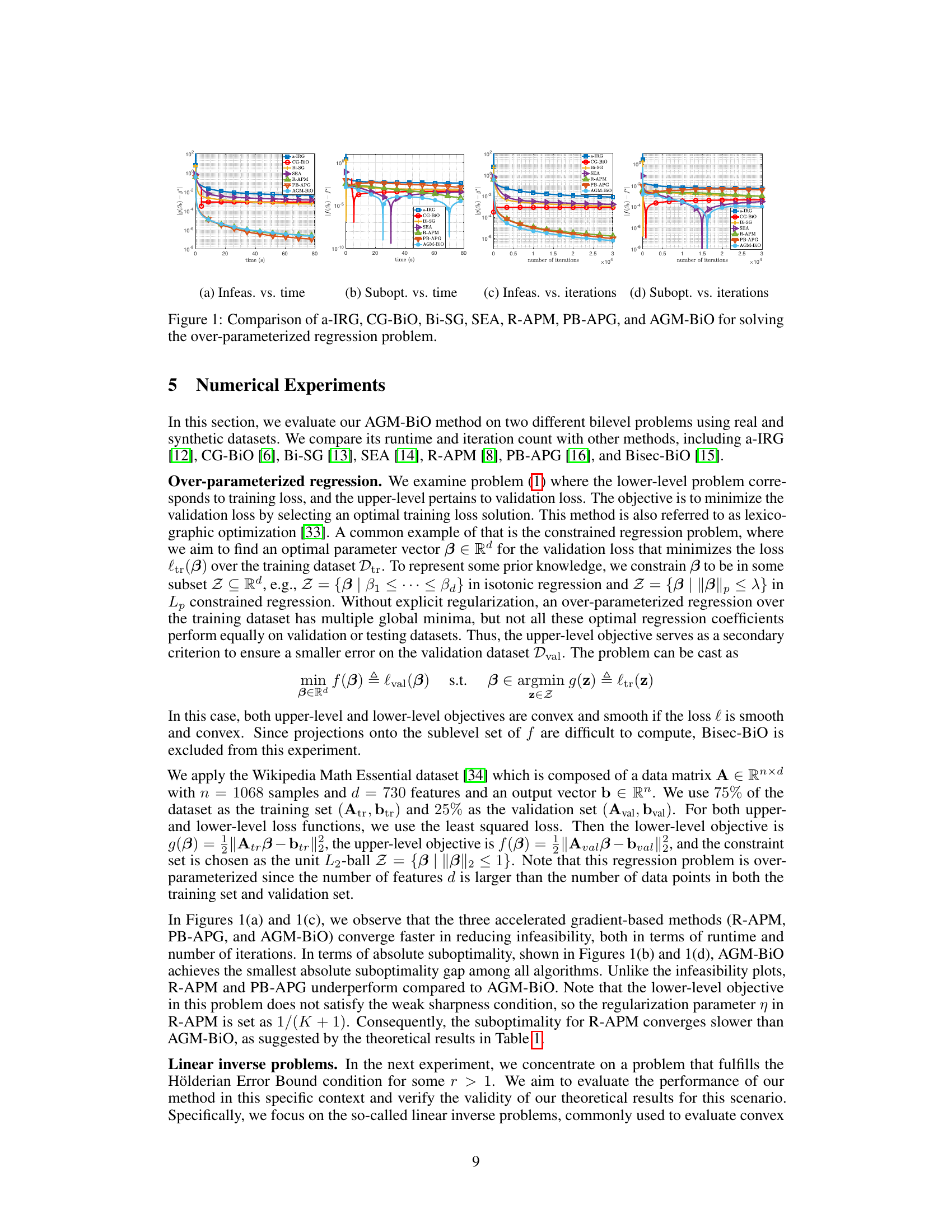
The figure compares seven different algorithms for solving an over-parameterized regression problem. The algorithms are evaluated based on their infeasibility (how far the solution is from satisfying the constraints) and suboptimality (how far the solution is from the optimal objective value). The comparison is shown over time and the number of iterations. The results show that the proposed AGM-BIO method generally performs the best in terms of both infeasibility and suboptimality.
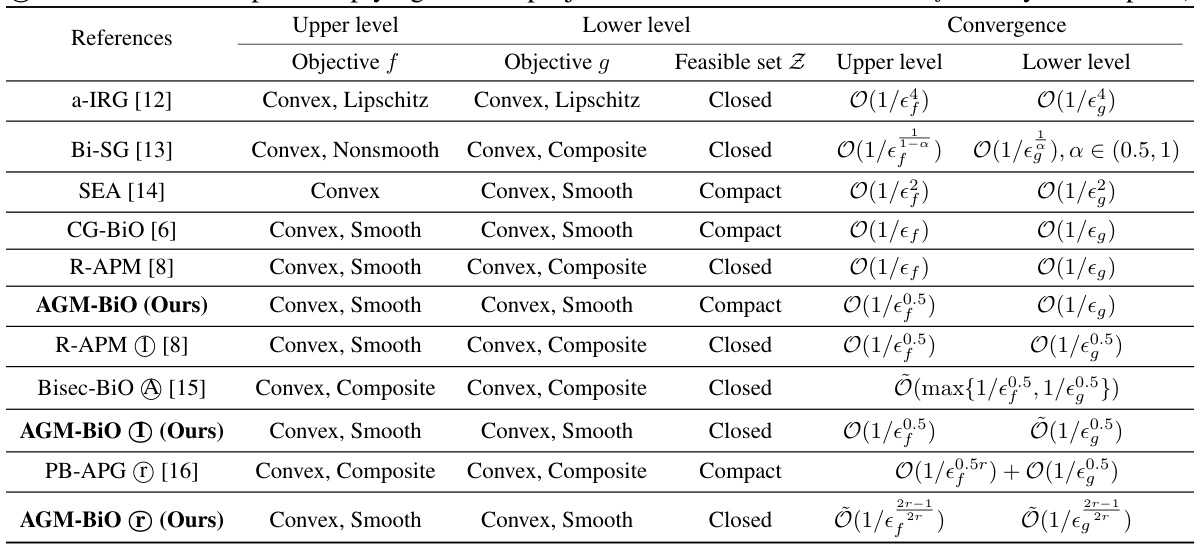
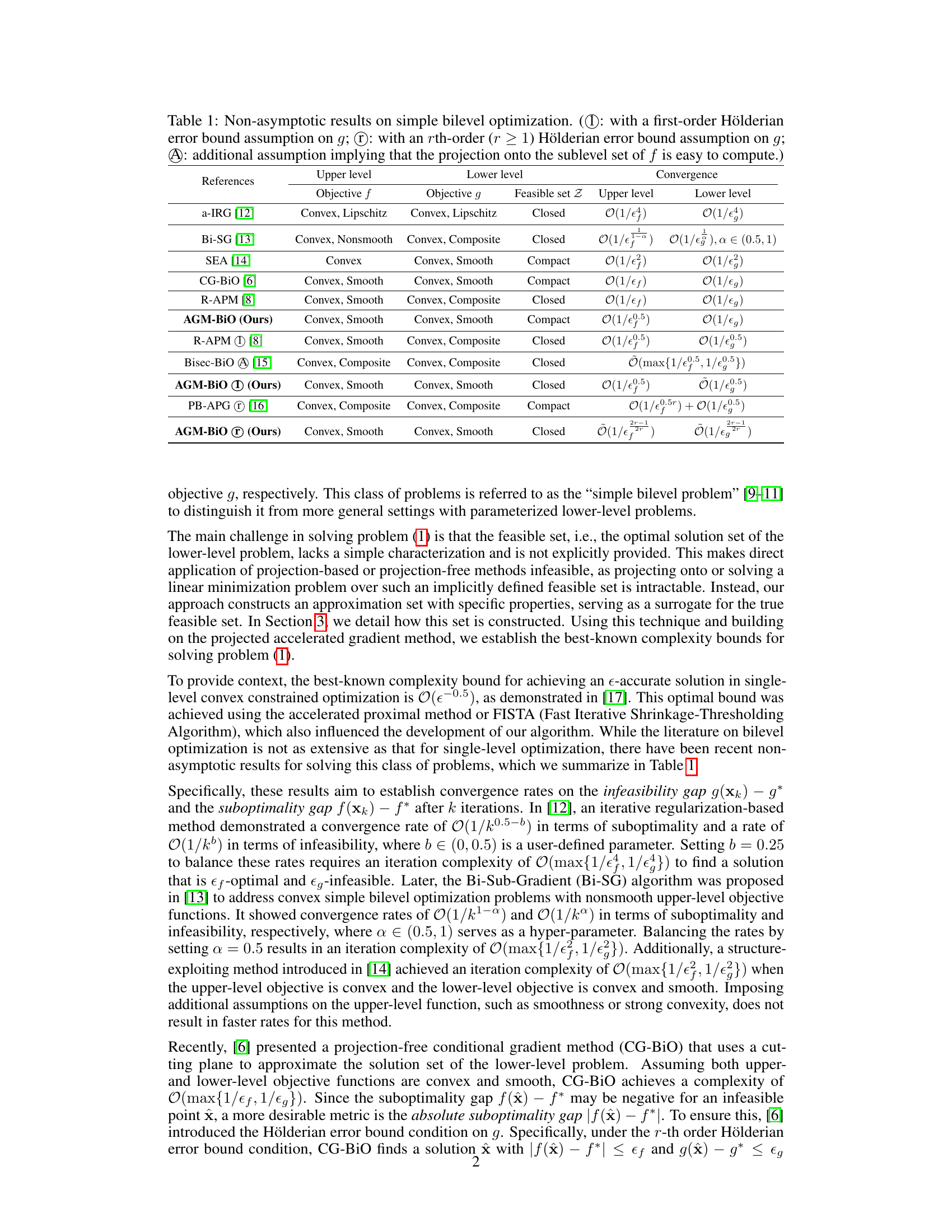
This table summarizes the non-asymptotic convergence rates of several existing simple bilevel optimization algorithms. It compares their performance in terms of upper-level suboptimality (f(x)-f*) and lower-level infeasibility (g(x)-g*), achieved after k iterations, under various assumptions on the objective functions (convexity, smoothness) and the feasible set (compactness, closedness). The table also notes if an algorithm uses a first-order or r-th order Hölderian error bound assumption (a regularity condition on the lower-level objective function), and if it requires an additional assumption related to the projection onto a sublevel set. The last column indicates the achieved convergence rate for both the upper and lower levels, highlighting that the AGM-BIO algorithm (the author’s proposed method) achieves optimal complexity under specific conditions.
Full paper#