↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Offline optimization is gaining popularity due to the high cost of online experiments. The core idea involves learning a surrogate model of the black-box function using existing data, but these surrogates often struggle with out-of-distribution (OOD) issues, leading to inaccurate predictions outside the original data regimes. Current solutions often involve problem-specific conditioning techniques, limiting their generalization to other models or tasks.
This research proposes IGNITE, a model-agnostic method that incorporates a model sharpness regularizer into surrogate training. This regularizer, based on surrogate gradient norm, is theoretically shown to reduce generalized sharpness on unseen data. Extensive experiments demonstrate IGNITE’s effectiveness across diverse tasks, achieving performance gains of up to 9.6%. This model-agnostic approach addresses limitations of existing techniques by offering a more generic and broadly applicable solution to the OOD problem in offline optimization.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel, model-agnostic approach to improve offline optimization, a crucial area in various scientific disciplines. The surrogate gradient norm regularization method is theoretically grounded and shows significant performance improvements across diverse tasks. This work offers new perspectives on sharpness regularization, opening avenues for further research and impacting existing offline optimizers.
Visual Insights#

This figure illustrates the concept of surrogate sharpness and how it can improve offline optimization. Panel (a) shows that a sharper surrogate model (ω₂) has a larger difference in prediction values between the model and the model with parameter perturbation, than a less sharp surrogate model (ω₁). Panel (b) demonstrates that by using a less sharp surrogate (ω₁), the optimizer is guided toward a solution closer to the actual optimum.

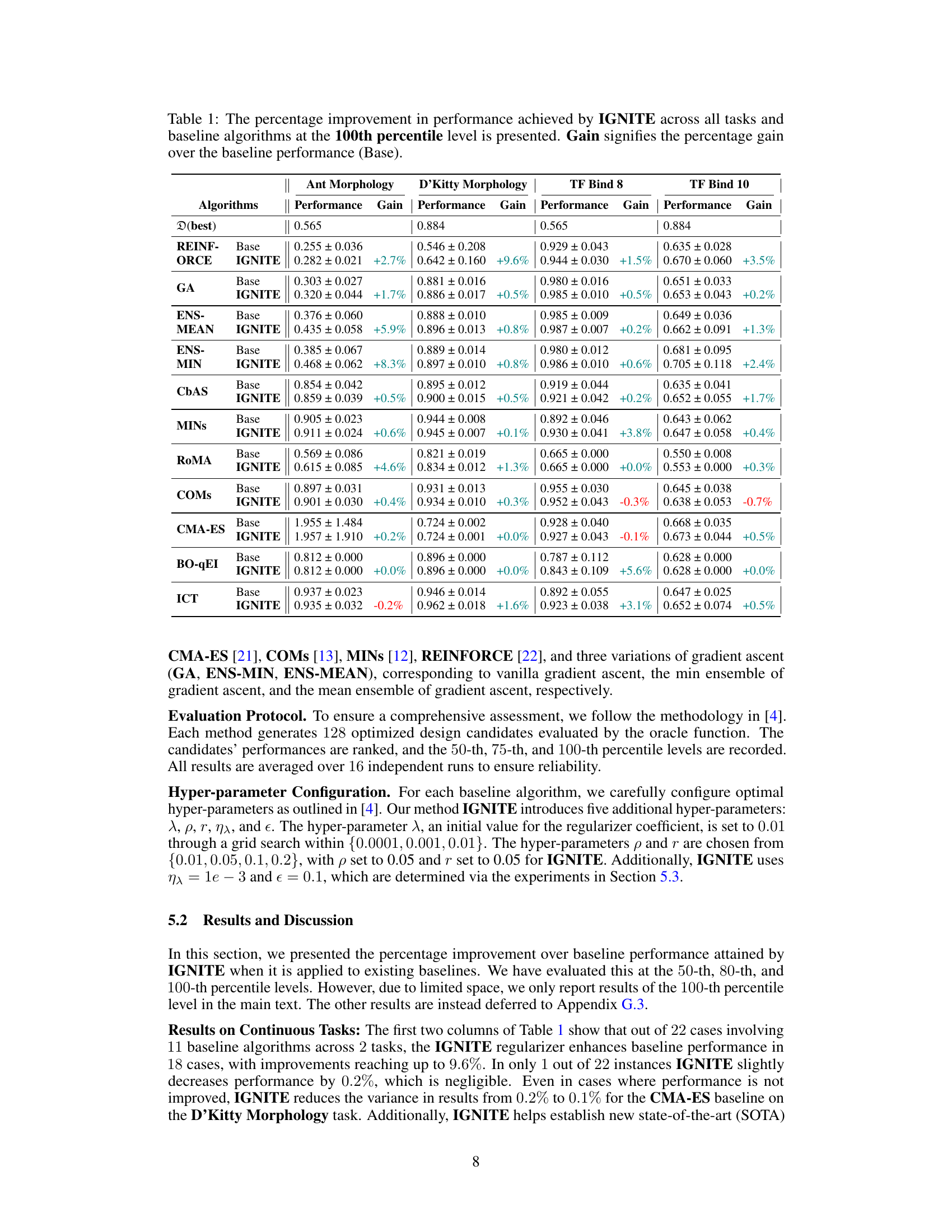
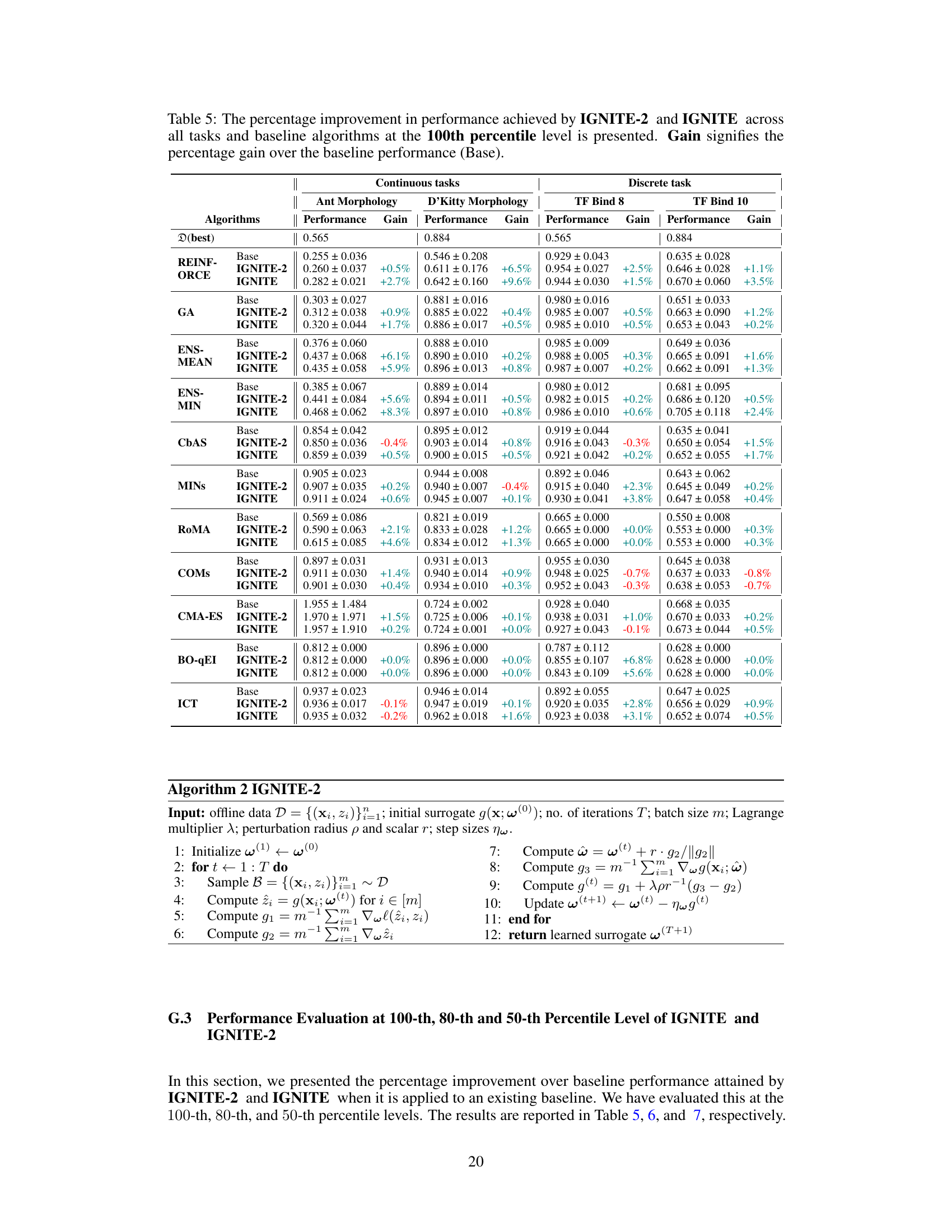
This table presents the performance improvement achieved by incorporating the proposed surrogate gradient norm (IGNITE) method into various existing offline optimization algorithms. It shows the percentage gain in performance at the 100th percentile (the best performing 1% of the results) for each algorithm across four different benchmark tasks. The table allows for a comparison of IGNITE’s effectiveness across a diverse set of optimization techniques and problem types.
In-depth insights#
Surrogate Sharpness#
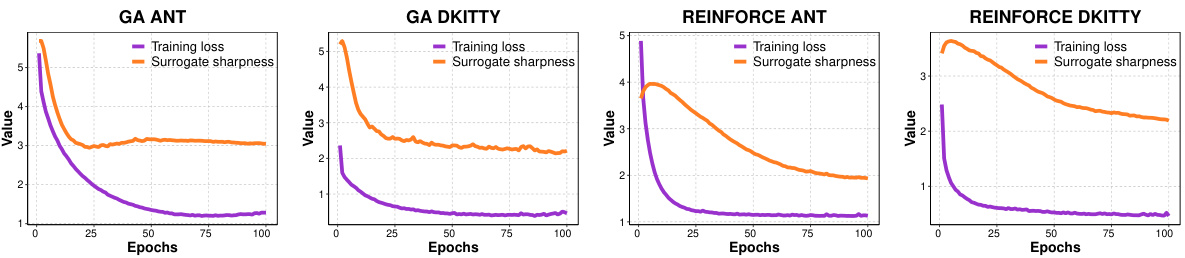
The concept of “Surrogate Sharpness” is central to the research paper’s proposed method for improving offline optimization. It addresses the out-of-distribution problem inherent in offline optimization, where surrogate models trained on historical data perform poorly on unseen data. Surrogate sharpness is defined as the maximum change in the surrogate model’s prediction across a small neighborhood of its parameters. A low sharpness indicates that the model’s output is relatively insensitive to small parameter perturbations. The key insight is that reducing surrogate sharpness on the training data provably reduces its generalized sharpness on unseen data, mitigating erratic predictions and boosting optimization performance. This is achieved by adding a constraint to the surrogate training process, limiting its gradient norm, thus making it less sensitive to parameter shifts. The theoretical analysis supports this claim by extending existing theories on sharpness regularization, providing a new perspective on how to limit the surrogate’s tendency for overestimating outputs in under-explored areas of the input space. The empirical results demonstrate that integrating this approach yields significant performance improvement across diverse optimization tasks.
IGNITE Algorithm#
The IGNITE algorithm, designed to enhance offline optimization, tackles the out-of-distribution problem by regularizing surrogate model sharpness. Instead of employing model-specific conditioning techniques, IGNITE uses a model-agnostic approach, incorporating a surrogate sharpness regularizer into the training loss. This approach is theoretically grounded, demonstrating that reduced surrogate sharpness on offline data leads to lower generalized sharpness on unseen data. Practical implementation involves approximating surrogate sharpness via the gradient norm, transforming the optimization into a constrained problem solved efficiently using existing constrained optimization solvers. Empirical results across diverse optimization tasks showcase IGNITE’s effectiveness, often leading to significant performance improvements. The model-agnostic nature of IGNITE is a key strength, making it applicable and beneficial to a wide variety of existing offline optimization methods.
Theoretical Analysis#
The theoretical analysis section of this research paper aims to provide a rigorous justification for the proposed approach of incorporating surrogate gradient norm as a regularizer. It seeks to demonstrate that reducing the surrogate’s sharpness on the offline dataset provably reduces its generalized sharpness on unseen data. This is a crucial contribution as it addresses the out-of-distribution problem common in offline optimization, where the learned model’s performance degrades significantly outside the training data regime. The analysis likely leverages existing theoretical frameworks concerning generalization bounds, extending these to specifically address surrogate model sharpness. A key aspect will be the establishment of a formal connection between empirical sharpness (measured on the training data) and generalized sharpness (measured on unseen data). This would likely involve probabilistic bounds and concentration inequalities to demonstrate that control over empirical sharpness translates to control over generalization performance. The theorems and proofs within this section should be carefully examined for their assumptions, conditions, and limitations. The soundness and scope of the theoretical analysis will critically determine the trustworthiness and applicability of the proposed approach.
Offline Optimization#
Offline optimization tackles the expensive cost of online experimentation by leveraging historical data to train a surrogate model. This model approximates the true objective function, enabling optimization without further real-world trials. A key challenge is the out-of-distribution (OOD) problem, where the surrogate model’s accuracy diminishes outside the range of the training data. Many approaches attempt to mitigate this by conditioning the surrogate model or search strategies, often with model-specific limitations. This paper introduces a model-agnostic method, incorporating a sharpness regularizer to constrain the surrogate’s gradient norm during training. This approach aims to improve generalization by reducing the model’s sensitivity to parameter perturbations. Theoretical analysis provides a formal justification for sharpness regularization, extending existing theories of loss sharpness to the surrogate sharpness. Empirical experiments demonstrate the effectiveness of this method across a range of tasks, yielding significant performance improvements.
Future Directions#
Future research could explore extending the surrogate gradient norm approach to more complex optimization landscapes and higher-dimensional spaces, addressing limitations in handling large-scale problems with high-dimensional input spaces. Investigating the synergy between surrogate sharpness and other regularization techniques could lead to even more robust offline optimization methods. A promising avenue is to develop adaptive sharpness control mechanisms that automatically adjust the sharpness based on the data distribution and model characteristics. Furthermore, theoretical work could focus on refining the bounds on generalized surrogate sharpness, potentially leading to tighter generalization guarantees and further improvements in performance. Finally, applying the proposed method to a broader range of applications beyond material design, such as reinforcement learning and robust optimization, would showcase its versatility and impact.
More visual insights#
More on figures

This figure shows the effect of hyperparameters epsilon (ε) and eta lambda (ηλ) on the performance improvement achieved by the proposed method IGNITE. The graphs illustrate how changes in these hyperparameters affect different algorithms (COMS and GA) and tasks (ANT and TF-Bind-10). This visualization helps in determining optimal values for ε and ηλ, which balance regularization and performance.

This figure compares the performance of the COMs and GA algorithms with and without the IGNITE-2 regularizer across different gradient ascent steps. It shows that IGNITE-2 improves the stability and performance of both algorithms, particularly in later optimization stages, on the ANT task. The results are less clear on the TF-BIND-10 task, but still show that adding the IGNITE-2 regularizer does not degrade performance.
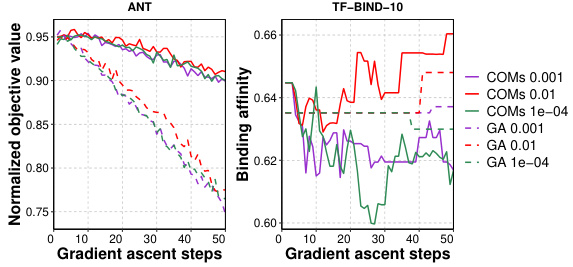
This figure shows the performance (normalized objective value or binding affinity) of two optimization algorithms (COMs and GA) with and without the IGNITE-2 regularizer over a certain number of gradient ascent steps. It illustrates the impact of the IGNITE-2 regularizer on the convergence and stability of the optimization process for two different tasks (ANT and TF-BIND-10). The plots show how the performance changes over time, comparing the baseline algorithms’ performance to that of algorithms that incorporate IGNITE-2. In some tasks, IGNITE-2 improves the optimization performance at later steps, while in others it may show performance improvements throughout the optimization process.
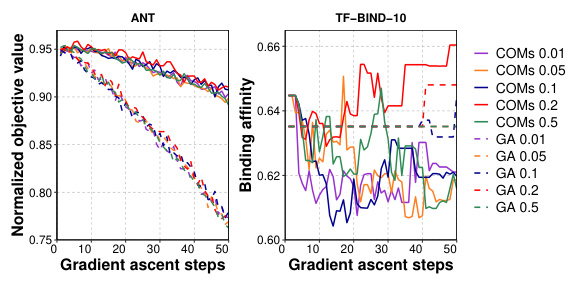
This figure displays the impact of hyperparameter tuning on the performance improvement achieved by IGNITE across different algorithms and tasks. Specifically, it shows how changing the threshold (ε) and step size (ηλ) in the proposed IGNITE method affects performance gains for both COMS and GA algorithms on the ANT and TF-BIND-10 tasks. The plots illustrate the sensitivity of the performance improvement to variations in these hyperparameters, helping to determine optimal values for effective regularization.

This figure demonstrates the impact of hyperparameters epsilon (ε) and eta lambda (ηλ) on the performance improvement achieved by the IGNITE method. Two baseline algorithms, COMS and GA, are tested across two different tasks, ANT and TF-BIND-10. The plots show how changes to ε (threshold) and ηλ (step size) affect the percentage improvement IGNITE provides over the baseline algorithms for each task. The results suggest that there’s an optimal range for these hyperparameters, outside of which the performance gain decreases or even becomes negative.
This figure illustrates the concept of surrogate sharpness and how it can improve offline optimization. Panel (a) shows that a surrogate model with lower sharpness (smaller change in prediction within a parameter neighborhood) will have predictions closer to the true optimal value if the true optimal parameters are within the neighborhood. Panel (b) demonstrates that using a sharpness-based regularizer during training leads to better predictions by selecting models whose predictions are less sensitive to small parameter perturbations, thus reducing the impact of out-of-distribution inputs.
More on tables
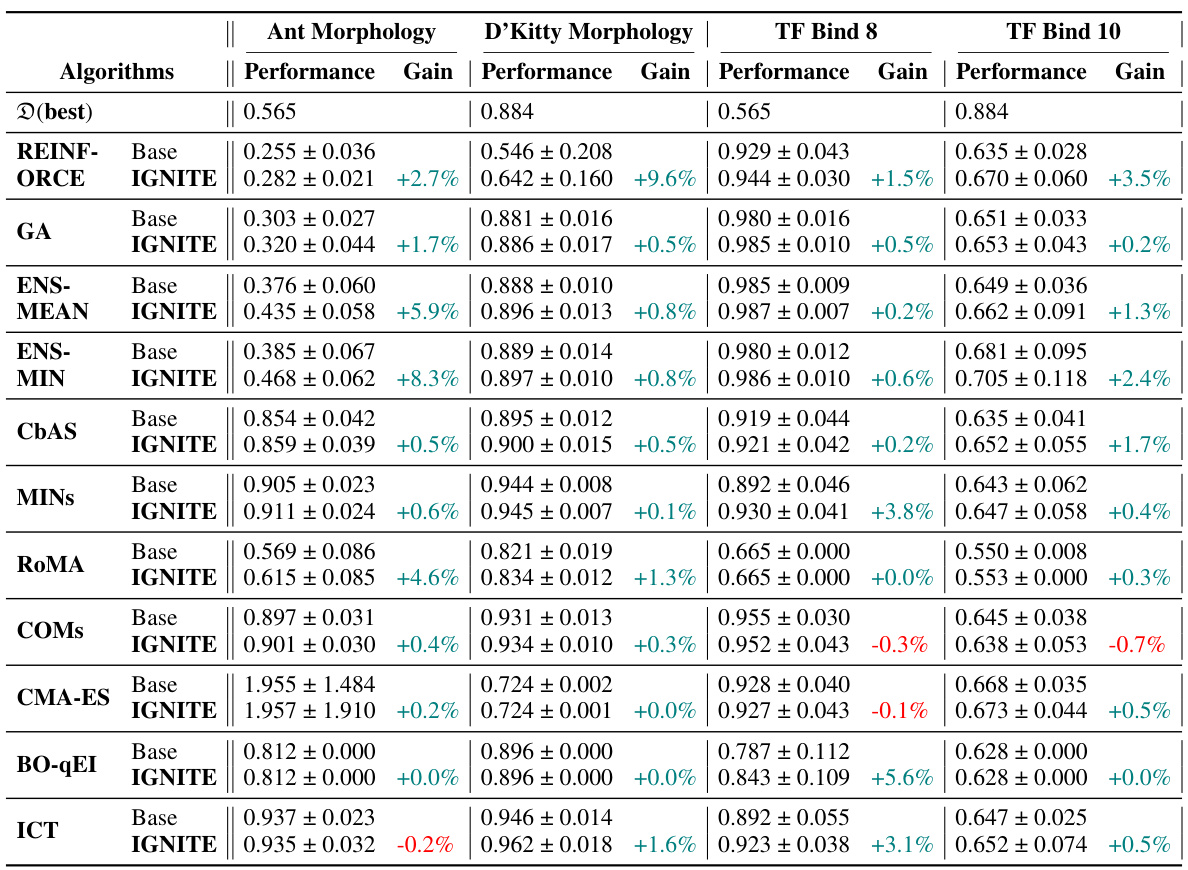
This table presents the performance improvement achieved by incorporating the proposed model-agnostic regularizer (IGNITE) into various existing offline optimization techniques across four benchmark tasks. The table shows the baseline performance for each algorithm on each task, along with the performance after applying IGNITE and the percentage gain or loss resulting from using IGNITE. The 100th percentile is used which represents the performance on the best candidate.
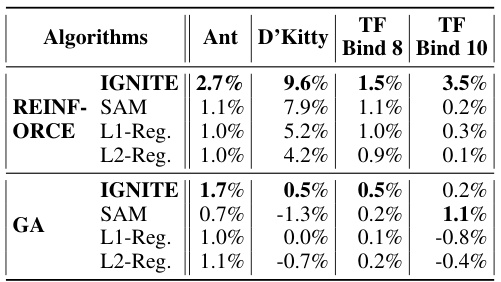
This table presents the performance improvement achieved by incorporating the proposed model-agnostic regularizer (IGNITE) into various existing offline optimization algorithms. It shows the percentage gain at the 100th percentile across four different tasks (Ant Morphology, D’Kitty Morphology, TF-Bind-8, and TF-Bind-10) for each algorithm. A positive percentage indicates an improvement in performance compared to the baseline algorithm without IGNITE, showcasing the effectiveness of the proposed method.
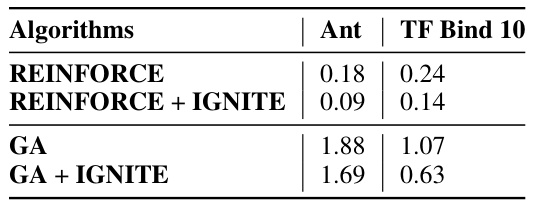
This table compares surrogate sharpness values, approximated by p||∇wh(w)||, for two algorithms (REINFORCE and GA) on two tasks (Ant and TF-Bind 10). Sharpness is calculated on unseen data (design candidates generated before and after using IGNITE). Lower sharpness values indicate improved generalization and performance.

This table shows the performance improvement achieved by incorporating the IGNITE regularizer into various offline optimization algorithms across four benchmark tasks. The improvements are measured at the 100th percentile (best-performing model) and expressed as a percentage increase over the baseline algorithm’s performance without IGNITE. The table highlights the consistent performance gains provided by IGNITE across different tasks and algorithms.
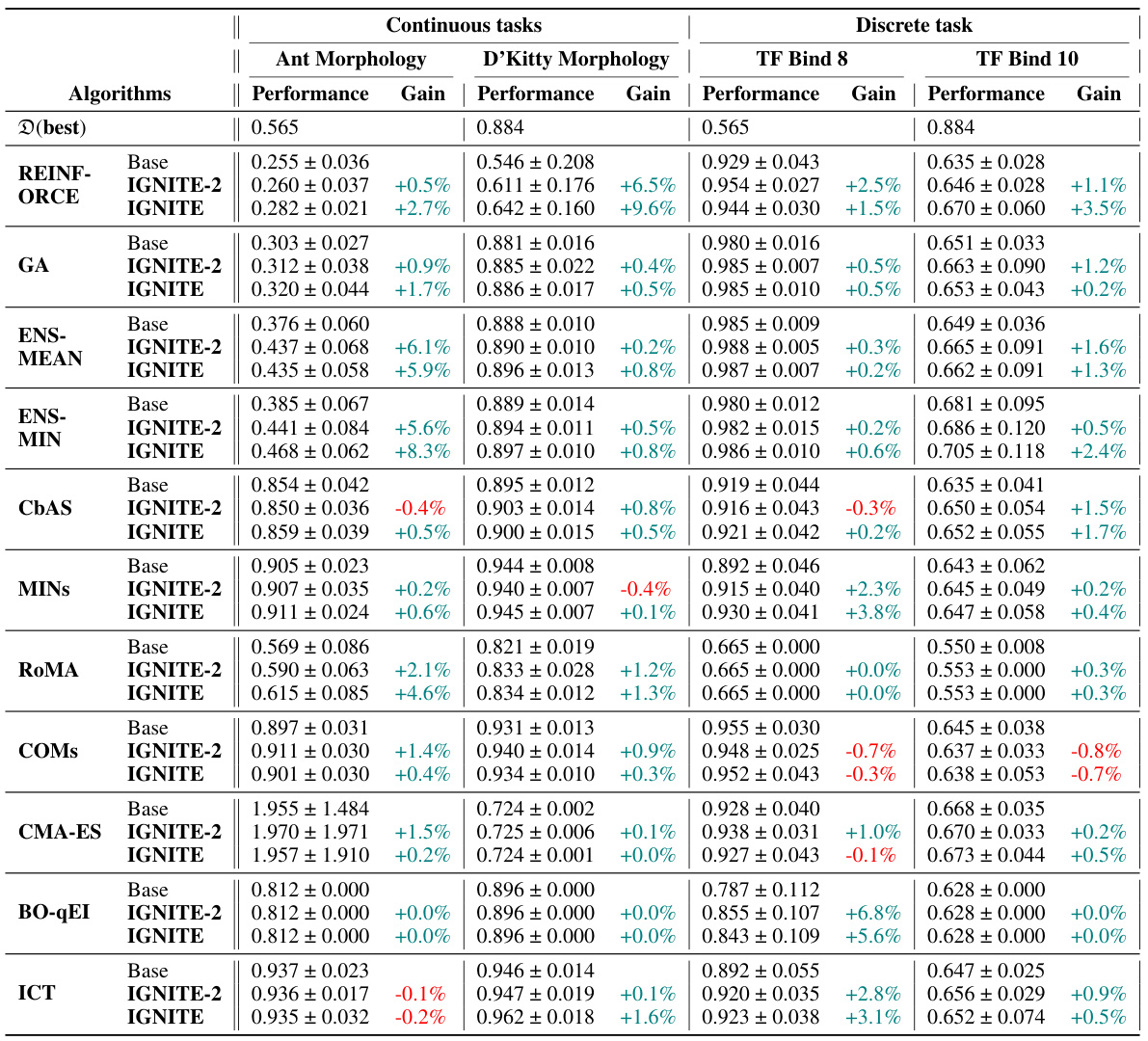
This table presents the performance improvement achieved by incorporating the IGNITE regularizer into various offline optimization algorithms across four benchmark tasks. The improvement is measured at the 100th percentile, representing the highest-performing candidate generated by each algorithm. The ‘Gain’ column shows the percentage increase in performance compared to the baseline algorithm without IGNITE, indicating the effectiveness of the proposed method in boosting performance. The table provides a comprehensive overview of how IGNITE enhances different optimization algorithms across diverse problem settings.

This table presents the performance improvement achieved by the proposed method, IGNITE, across various tasks and baseline algorithms. The improvement is measured at the 100th percentile, representing the best-performing model’s performance. The ‘Gain’ column shows the percentage improvement compared to each baseline algorithm.
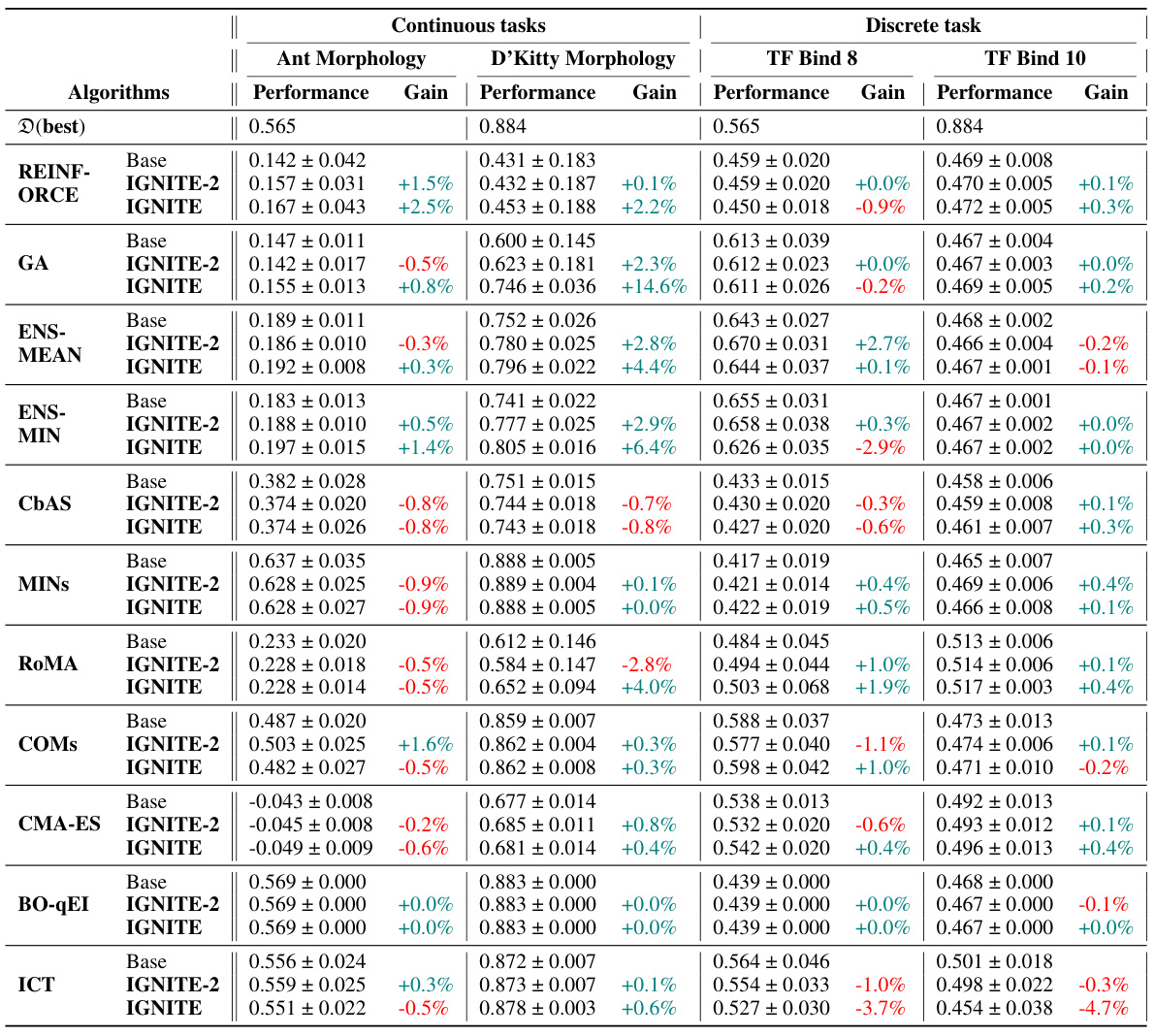
This table presents the performance improvement achieved by incorporating the proposed method, IGNITE, into various existing offline optimization algorithms. The results are shown for four different tasks across a range of baseline algorithms. The improvement is measured at the 100th percentile, representing the best-performing candidate in each trial. ‘Gain’ shows the percentage increase compared to the baseline performance of each algorithm for each task.

This table presents the performance improvement achieved by incorporating the IGNITE regularizer into various baseline offline optimization algorithms across four different tasks. The improvement is measured at the 100th percentile, representing the best-performing candidate in each run. The ‘Gain’ column shows the percentage increase in performance compared to the baseline algorithm without IGNITE. The table provides a concise summary of IGNITE’s effectiveness across diverse optimization scenarios.
Full paper#