↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Standard reinforcement learning struggles with exploration-exploitation trade-offs, particularly when early exploration sacrifices immediate rewards for long-term gains. Existing meta-RL methods, aiming to maximize cumulative rewards, often get stuck in suboptimal solutions due to this early reward penalty. This significantly limits their performance on complex tasks.
The proposed approach, First-Explore, tackles this by training separate exploration and exploitation policies. The exploration policy focuses solely on gathering information, while the exploitation policy aims to maximize returns using the gathered information. By learning these two policies independently and then combining them, First-Explore enables efficient exploration, even when it means sacrificing immediate gains. This approach leads to significantly improved cumulative rewards compared to traditional meta-RL algorithms.
Key Takeaways#
Why does it matter?#
This paper is important because it identifies a critical limitation in existing meta-reinforcement learning (meta-RL) methods and proposes a novel solution. The findings challenge the assumption that directly optimizing for cumulative reward is always optimal and open new avenues for designing more robust and human-like exploration strategies in RL agents. This is particularly relevant given the increasing interest in applying RL to complex real-world tasks where exploration is crucial but challenging.
Visual Insights#

This figure illustrates the First-Explore algorithm’s three phases: policy training, k-selection, and final policy. In the training phase, two separate policies (explore and exploit) are trained using context from previous episodes. The k-selection phase determines the optimal balance between exploration and exploitation by testing different numbers of initial exploration episodes. Finally, the best combination of exploration and exploitation episodes is used for inference.

This table presents the mean cumulative reward and standard deviation achieved by First-Explore and other algorithms (including baselines) across three challenging domains: Bandits with One Fixed Arm, Dark Treasure Rooms, and Ray Maze. The results show that First-Explore significantly outperforms existing cumulative reward meta-RL algorithms (RL2, VariBAD, HyperX) in scenarios where optimal behavior requires sacrificing immediate reward for greater future reward. Random actions are included for comparison.
In-depth insights#
Exploration Tradeoffs#
Exploration-exploitation trade-offs represent a core challenge in reinforcement learning. Balancing the need to explore unfamiliar parts of the environment to discover potentially higher rewards with the need to exploit already known high-rewarding actions is crucial for optimal performance. The inherent difficulty arises because exploration often necessitates sacrificing immediate rewards for potentially greater long-term gains, making it challenging for agents to learn effective strategies. Traditional methods often struggle to solve complex exploration problems where short-term losses are necessary for eventual success. Human-like intelligence excels at navigating these trade-offs, but replicating this adaptability remains a significant hurdle for artificial agents. Advanced meta-learning techniques show promise in tackling these challenges by learning to explore effectively across various scenarios. However, even meta-learning approaches face limitations, sometimes becoming trapped in local optima that hinder exploration if there’s a need to forgo immediate reward. Novel methods are needed to address the limitations of existing approaches and ultimately develop agents that can seamlessly handle both exploration and exploitation with human-level proficiency.
First-Explore Method#
The First-Explore method is a novel meta-reinforcement learning approach designed to overcome limitations of existing cumulative-reward methods. Instead of training a single policy to maximize cumulative reward, it trains two separate policies: one for exploration and one for exploitation. This decoupling addresses the crucial issue where optimizing cumulative reward directly can hinder exploration, particularly when early exploration sacrifices immediate reward for higher long-term gains. The exploration policy focuses on generating informative episodes without maximizing immediate rewards, thus encouraging the discovery of beneficial states for the exploitation policy. The exploitation policy, on the other hand, aims to maximize reward within a given context provided by the exploration policy. After independent training, both policies are combined to determine an optimal exploration-exploitation balance, yielding superior performance in challenging environments where exploration is essential for achieving high cumulative reward. This two-pronged approach effectively prevents the agent from getting stuck in suboptimal local optima due to short-sighted reward maximization. This method represents a significant step toward developing meta-RL algorithms capable of human-like exploration strategies.
Cumulative Meta-RL#
Cumulative Meta-RL aims to optimize an agent’s performance across a sequence of episodes by maximizing the total reward accumulated. A key challenge arises when optimal behavior necessitates sacrificing immediate rewards for greater future gains. Standard cumulative Meta-RL methods often fail in such scenarios, becoming trapped in suboptimal local optima due to the short-sighted nature of reward maximization. This limitation stems from the inherent conflict between exploration (potentially sacrificing immediate reward) and exploitation (maximizing current reward). Effective exploration strategies, which are crucial for overcoming this trade-off, are often complex and difficult to learn. The need to forgo immediate rewards for potentially higher future rewards is a significant factor contributing to this failure, making these methods inadequate in domains that require such exploration. This shortcoming underscores the limitations of directly optimizing cumulative rewards and highlights the necessity for more sophisticated meta-learning approaches that explicitly address the exploration-exploitation dilemma.
Limitations & Future#
The section ‘Limitations & Future Work’ in a research paper is crucial for demonstrating a balanced perspective. It should acknowledge the study’s shortcomings and suggest avenues for future research. Identifying limitations such as the scope of the study (specific environments tested, limited algorithms compared), methodological choices (specific training methods used), or assumptions made (about reward dynamics, environmental properties), is essential. Suggesting improvements could involve exploring broader ranges of environments, comparing with a wider variety of algorithms, testing robustness against different conditions, or refining the methodology. Future directions may propose extensions of the current work to address those limitations, such as developing new algorithms or theoretical models, or adapting the current approach to new domains or problems. A well-written section demonstrates self-awareness and guides future research effectively.
Benchmark Domains#
A well-designed benchmark suite for reinforcement learning (RL) is crucial for evaluating the progress of exploration-exploitation algorithms. Benchmark domains should ideally capture the nuances of real-world problems, including environments that require significant exploration before exploitation becomes effective. The challenges of balancing exploration and exploitation are often exacerbated in situations where exploration incurs an immediate cost or delayed reward, making the assessment of algorithms particularly complex. A strong benchmark should encompass a range of difficulty levels, from simple problems where exploration is straightforward to extremely challenging ones that test the limits of current RL methods. Furthermore, the benchmark needs to be robust and generalizable, ensuring that evaluation isn’t skewed by specific domain characteristics or easily exploited by overly specialized algorithms. Careful consideration of domain properties, such as reward sparsity, state-space complexity, and the presence of deceptive traps or misleading cues, are needed to create a truly representative and effective benchmark that will ultimately advance the field of RL.
More visual insights#
More on figures
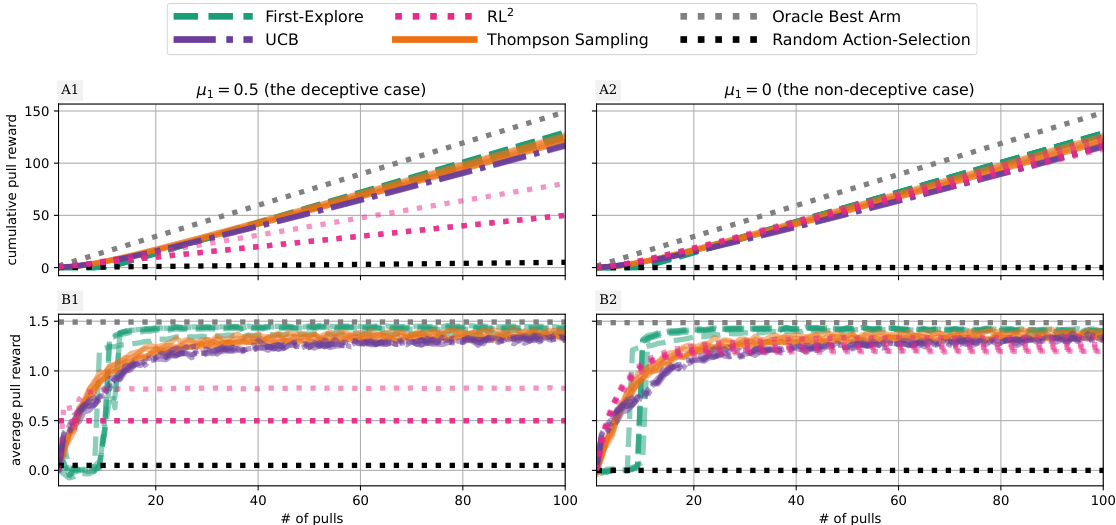
This figure is an alternative visualization of Figure 2, showing the mean cumulative and average pull rewards with standard deviation across multiple runs for both the deceptive (μ₁ = 0.5) and non-deceptive (μ₁ = 0) cases. It displays the performance of First-Explore, UCB, Thompson Sampling, RL2, the oracle (always choosing the best arm), and random action selection. The standard deviations help illustrate the variability in performance across different bandit instances.
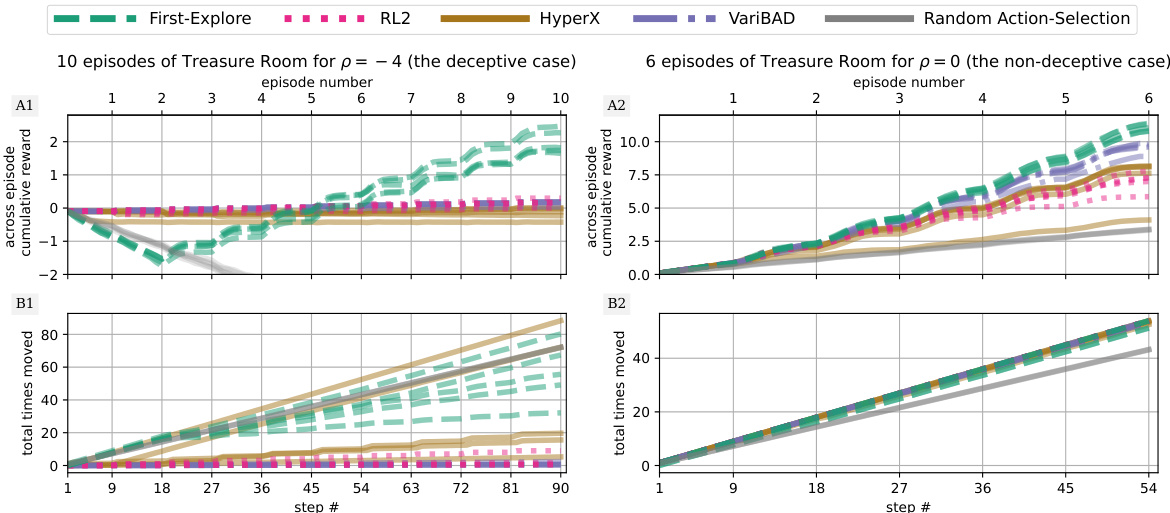
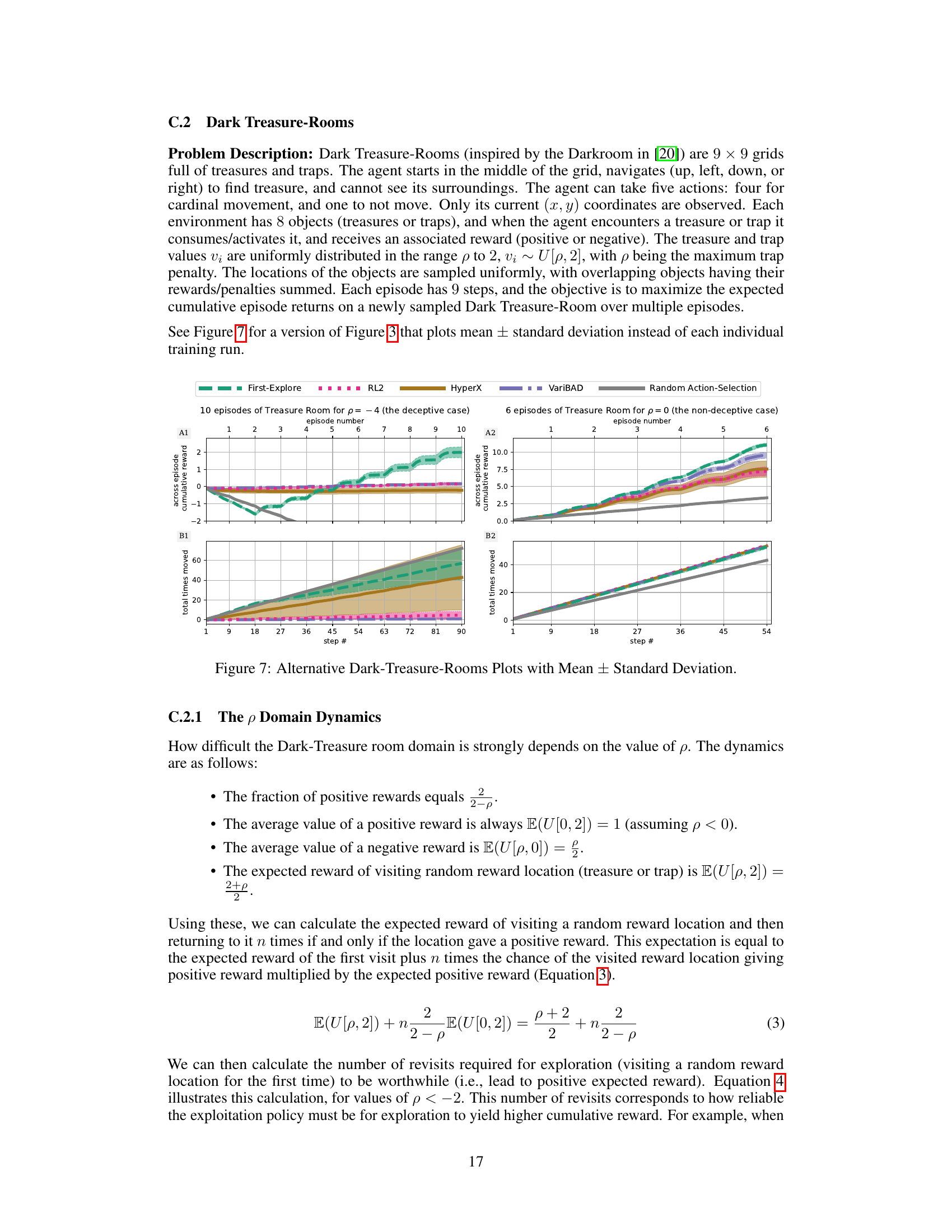
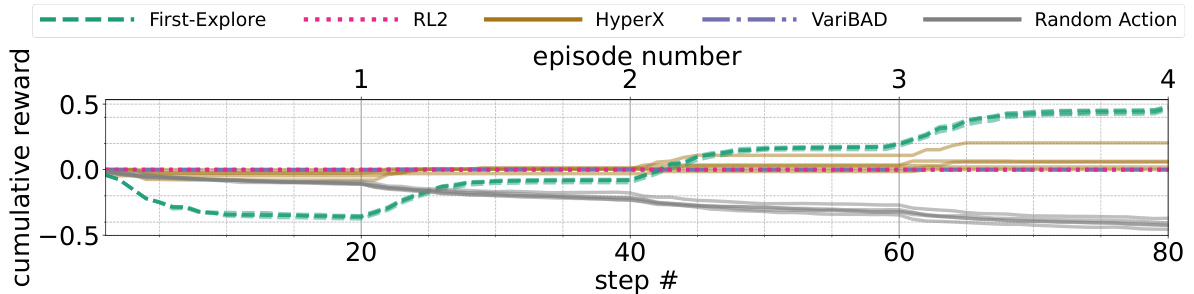
The figure shows the performance comparison between First-Explore and other meta-RL algorithms (RL2, VariBAD, HyperX) on the Dark Treasure Room environment, both in deceptive (p = -4) and non-deceptive (p = 0) settings. The plots illustrate cumulative reward over time, along with a measure of exploration (total moves made). It highlights First-Explore’s superior performance, particularly in the deceptive case where other methods fail due to their avoidance of exploration.
The figure compares the performance of First-Explore and three other meta-RL algorithms (RL2, HyperX, VariBAD) on the Dark Treasure Room domain under deceptive and non-deceptive conditions. It shows that First-Explore significantly outperforms the other algorithms in the deceptive condition where early exploration requires sacrificing immediate reward. The plots illustrate cumulative reward, episode reward, and the number of times the agent moves, highlighting First-Explore’s ability to balance exploration and exploitation effectively.
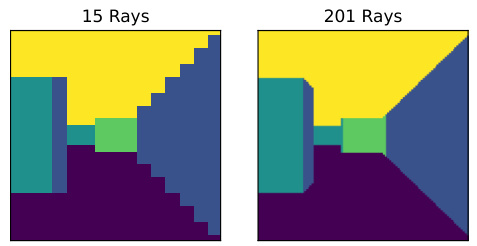
The figure shows a comparison between the raw lidar observations (15 rays) received by the agent in the Ray Maze environment and a complete image of the environment generated using all available lidar data (201 rays). The raw observations are converted into an image where goal locations are shown in green, east-west walls in teal, north-south walls in navy, the floor in dark purple, and the sky in yellow. This demonstrates the limited perceptual capability of the agent, which must navigate the maze based only on the sparse sensor data.

The figure compares the performance of First-Explore and other algorithms (including specialized bandit algorithms) on deceptive and non-deceptive bandit tasks. It shows that First-Explore significantly outperforms other methods, especially in the deceptive case where early exploration sacrifices immediate reward for higher long-term returns.
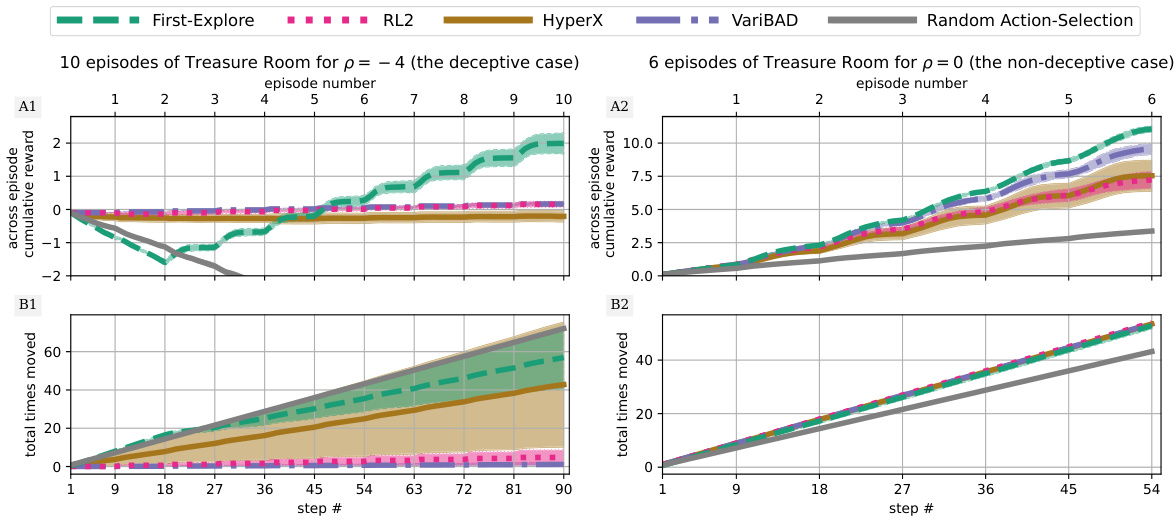
This figure compares the performance of First-Explore and several other meta-RL algorithms on the Dark Treasure Room environment under deceptive and non-deceptive conditions. It shows that First-Explore significantly outperforms the other methods in the deceptive case (where exploration requires sacrificing immediate rewards), demonstrating its ability to learn effective exploration strategies despite this challenge. In the non-deceptive case, First-Explore still performs well, although the performance differences are less pronounced.
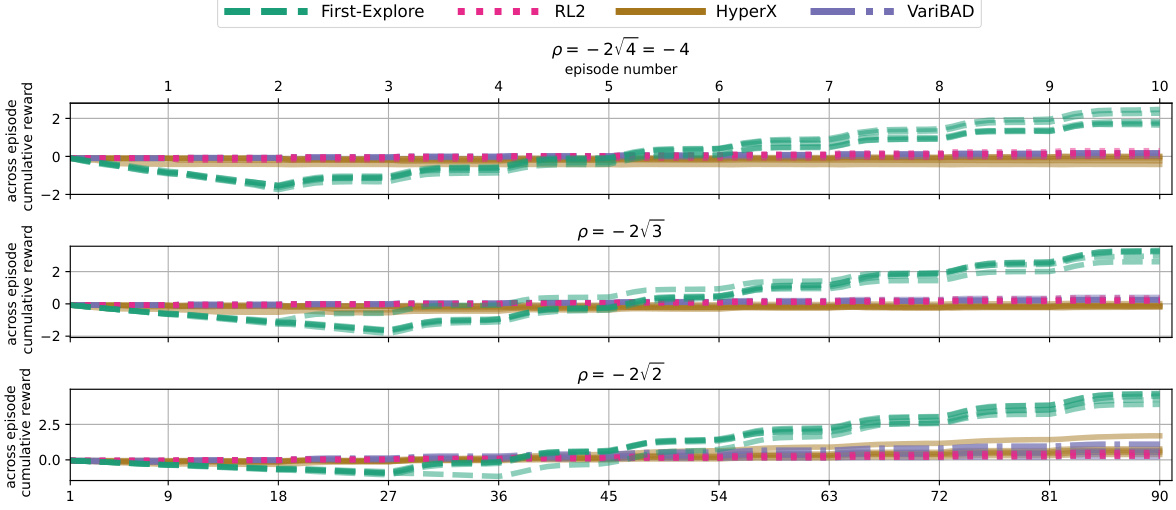
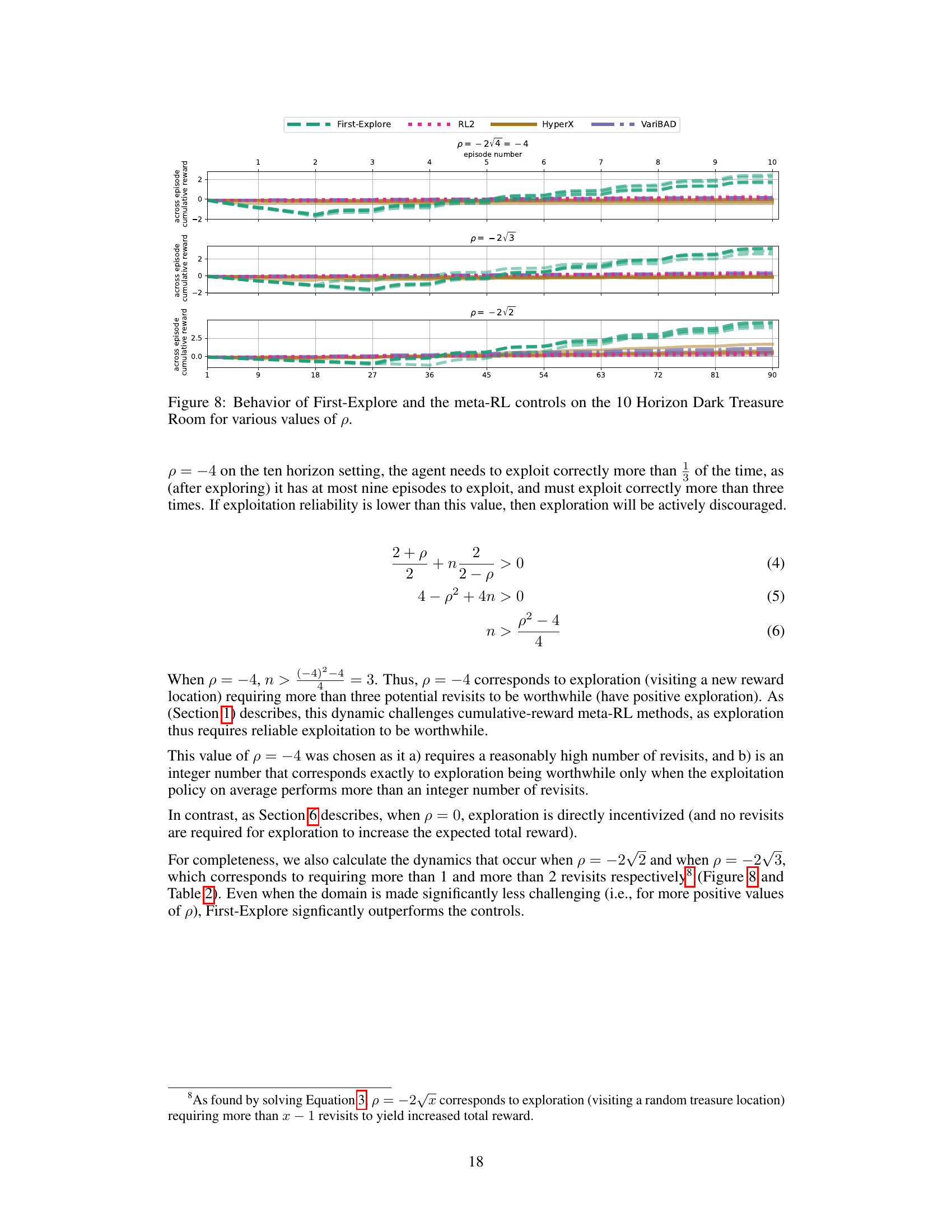
This figure shows the performance of First-Explore and three other meta-reinforcement learning algorithms (RL2, VariBAD, and HyperX) across different values of the parameter ‘p’ in the 10-horizon Dark Treasure Room environment. The x-axis represents the episode number, and the y-axis represents the cumulative reward across episodes. Different values of ‘p’ represent different levels of difficulty in the environment, with lower values being more difficult because they require the agent to sacrifice immediate reward early in the episode sequence to achieve higher rewards later. This figure demonstrates First-Explore’s ability to achieve significantly better performance than other algorithms, especially in challenging environments (lower p-values).

This figure compares the performance of First-Explore against three other meta-RL algorithms (RL2, HyperX, and VariBAD) and random actions on two versions of the Dark Treasure Room environment: deceptive (p = -4) and non-deceptive (p = 0). The top row shows cumulative reward over episodes and steps, and the bottom row shows the number of times agents move, indicating exploration. In the deceptive setting, where forgoing immediate rewards is necessary for optimal long-term performance, First-Explore outperforms the other algorithms. However, in the non-deceptive setting, all algorithms perform well. The results highlight First-Explore’s ability to succeed in scenarios where other methods fail due to an inability to balance exploration and exploitation.

This figure shows the average cumulative reward achieved by RL2, VariBAD, and HyperX across multiple training runs with varying lengths for the deceptive Dark Treasure Room environment. The top panel displays the performance of all three algorithms across 100% of the training progress. The bottom panel shows the effect of changing the number of episode steps used during HyperX training (2e6, 2e7, and 2e8). The results demonstrate that even with significantly more training, the algorithms still fail to achieve satisfactory cumulative reward, highlighting a limitation of optimizing directly for cumulative reward in environments requiring reward-sacrificing exploration. The consistent low performance across different training lengths for HyperX further suggests that the algorithm’s exploration bonus schedule, rather than insufficient training, is the primary factor contributing to its poor performance.
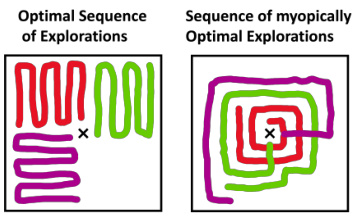
This figure illustrates the difference between a sequence of myopically optimal explorations and an optimal sequence of explorations. A myopic strategy prioritizes immediate reward, leading to suboptimal long-term exploration. In contrast, an optimal sequence plans exploration steps to maximize overall exploration efficiency, even if it means sacrificing immediate gains in some steps.
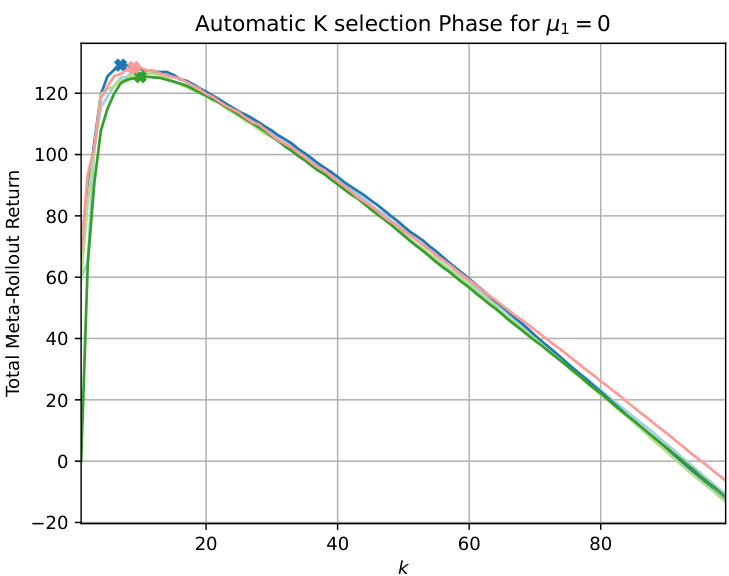
This figure shows the results of the k-selection phase of the First-Explore algorithm. The x-axis represents the number of exploration episodes (k), and the y-axis represents the total meta-rollout return. Five different training runs are shown, each with a different peak return, indicating the algorithm’s sensitivity to the balance between exploration and exploitation. The selected k value for each run is the one that maximizes the return, shown by the cross on each curve.

This figure shows a sample visualization of the Dark Treasure Room environment. The agent’s current position is a blue square. Green squares represent positive rewards, and red squares represent negative rewards, with intensity representing magnitude. When the agent lands on a square, the color blends to reflect both the agent and reward colors.
The figure illustrates the First-Explore algorithm’s workflow. It consists of three phases: Policy Training, k-Selection, and Final Policy. In the Policy Training phase, two separate policies are trained – one for exploration and one for exploitation. The exploration policy focuses on generating informative episodes, while the exploitation policy aims to maximize immediate reward. During training, the exploration policy provides context (past episodes) to both policies. In the k-Selection phase, different combinations of the trained policies are evaluated to determine the optimal balance between exploration and exploitation (number of initial exploration episodes k before switching to exploitation). The Final Policy phase uses the best combination from the k-Selection phase for inference (new environments): exploring for k episodes and then exploiting for the rest.

This figure illustrates the First-Explore algorithm. It shows how two separate policies, one for exploration and one for exploitation, are trained and then combined to maximize cumulative reward across multiple episodes. The exploration policy informs the exploitation policy by providing contextual information from previous episodes, and the success of the exploitation policy provides feedback for improving the exploration policy. Finally, the algorithm determines the optimal balance between exploration and exploitation by evaluating different combinations of the two policies.

This figure illustrates the First-Explore algorithm, which maximizes cumulative reward by training two separate policies: an explore policy and an exploit policy. The explore policy focuses on gathering information, while the exploit policy focuses on maximizing reward. The algorithm combines these policies after training, using a k-selection phase to determine the optimal balance between exploration and exploitation for new environments.

The figure shows the First-Explore framework for meta-RL. It trains two separate policies: an explore policy and an exploit policy. The explore policy focuses on gathering information, while the exploit policy aims to maximize immediate reward. These policies are trained separately and then combined optimally to maximize cumulative reward in a sequence of episodes. The diagram illustrates the training and k-selection phases, emphasizing the flow of information (context) between the two policies.
The figure illustrates the First-Explore algorithm’s process of maximizing cumulative reward. It involves training two separate policies: one for exploration and one for exploitation. The exploration policy informs the exploitation policy, which then maximizes rewards. Different combinations of exploration and exploitation lengths are tested, and the best combination is selected for inference.
More on tables

This table shows the mean cumulative reward and standard deviation achieved by First-Explore and three other meta-RL algorithms (RL2, VariBAD, and HyperX) across 10 episodes in the Dark Treasure Room environment. The environment’s difficulty is parameterized by p, where a higher absolute value of p makes exploration more challenging, as it requires more consistent exploitation to make exploration worthwhile. The results demonstrate that First-Explore significantly outperforms the other algorithms across all values of p, highlighting its effectiveness in environments that require sacrificing immediate reward for long-term gains.

This table presents the results of the Bandits with One Fixed Arm experiment, comparing the performance of First-Explore to three other algorithms: RL2, UCB1, and Thompson Sampling. The experiment was conducted with two settings: one where the first arm has an above-average reward (the deceptive setting) and one where it does not (the non-deceptive setting). The mean and standard deviation of the cumulative reward are reported for each algorithm and setting. The UCB1 and Thompson Sampling algorithms are non-meta-RL baselines included for comparison.
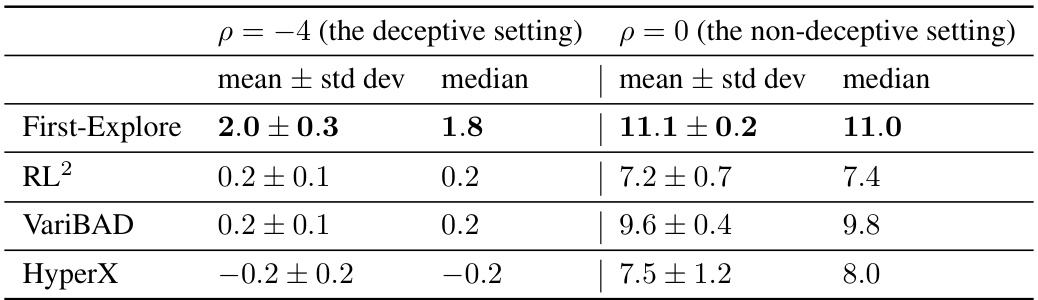
This table presents the mean and median cumulative rewards achieved by First-Explore and three other meta-RL algorithms (RL2, VariBAD, and HyperX) in the Dark Treasure Room environment under two different reward settings: a deceptive setting (p = -4) and a non-deceptive setting (p = 0). The deceptive setting makes exploration less immediately rewarding, creating a challenging scenario for cumulative reward methods. The table highlights the significant performance difference between First-Explore and the other algorithms, especially in the deceptive setting, demonstrating First-Explore’s ability to handle environments where early exploration requires foregoing immediate rewards.
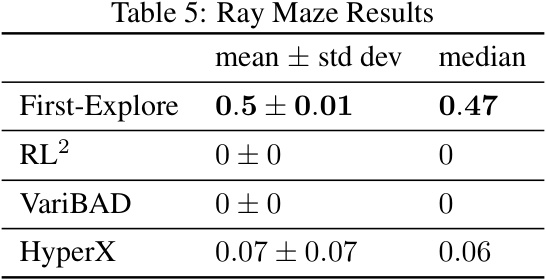
This table presents the mean cumulative reward and standard deviation achieved by First-Explore and several baseline algorithms across three different challenging domains. The results demonstrate First-Explore’s significant outperformance in scenarios requiring the agent to sacrifice immediate reward for long-term gain, a key challenge that existing meta-RL methods struggle with. The bandit domain also includes comparisons to non-meta RL baselines.

This table presents the compute time required for training different models on various tasks. It highlights that many of the meta-RL control models converged to a solution quickly and didn’t benefit from extended training. To save computational resources, the training time for these models was shorter than that of the First-Explore model. The symbol † indicates tasks where this early convergence occurred.

This table shows the mean cumulative reward and standard deviation for the Bandits with One Fixed Arm environment. The results for First-Explore are compared against three other algorithms (RL2, UCB-1, and Thompson Sampling). The table also includes the median cumulative reward for each algorithm. Two versions of the bandit problem are included: one where early exploration sacrifices immediate reward, and another where it does not. The † symbol indicates non-meta-RL baselines.

This table presents the mean cumulative reward and its standard deviation achieved by First-Explore and several control algorithms across three different domains: Bandits with One Fixed Arm, Dark Treasure Rooms, and Ray Maze. The results demonstrate that First-Explore significantly outperforms the other algorithms in these domains, particularly when exploration requires sacrificing immediate reward for greater future reward. A random action baseline is included for comparison, and the bandit domain also provides results from two additional non-meta-RL baselines (UCB and Thompson Sampling). The † symbol marks non-meta-RL baselines.

This table presents the hyperparameters used for training the rollout policies (explore and exploit) in the First-Explore framework. It shows the settings for three different domains: Bandits, Darkroom, and Ray Maze. The parameters cover temperature for sampling actions in both explore and exploit policies, the frequency of policy updates, the probability of randomly selecting an action (epsilon), the baseline reward used during training, and the total number of training updates performed. These parameters were carefully chosen to ensure effective training for each of the distinct tasks and complexities of the domains.
Full paper#