↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
This paper tackles the challenge of determining the minimax regret (the worst-case performance compared to the best possible strategy) for two important types of online learning problems. The first is multi-armed bandits with expert advice, where a learner chooses between multiple options, guided by expert recommendations. The second problem is contextual linear bandits, which is a more general setting where the learner’s choices also depend on the context or situation. Prior research had left a gap between the best-known upper and lower bounds on the minimax regret for these problems.
The researchers develop novel algorithms to address the gaps between upper and lower bounds identified in the existing literature. They achieve a significant improvement for contextual linear bandits using a follow-the-regularized-leader approach with a Tsallis entropy regularizer. They also prove matching lower bounds, showing that their algorithms are essentially the best possible in certain settings. This work provides valuable insights for both theoretical analysis and the design of improved algorithms for online learning problems.
Key Takeaways#
Why does it matter?#
This paper is important because it closes the gap in understanding the minimax regret for two crucial online learning problems: multi-armed bandits with expert advice and contextual linear bandits. It provides novel algorithms and matching lower bounds, advancing the theoretical understanding of these widely-used models and informing the design of more efficient algorithms. This work directly addresses open questions posed by previous studies, stimulating further research into optimal strategies and more general settings.
Visual Insights#
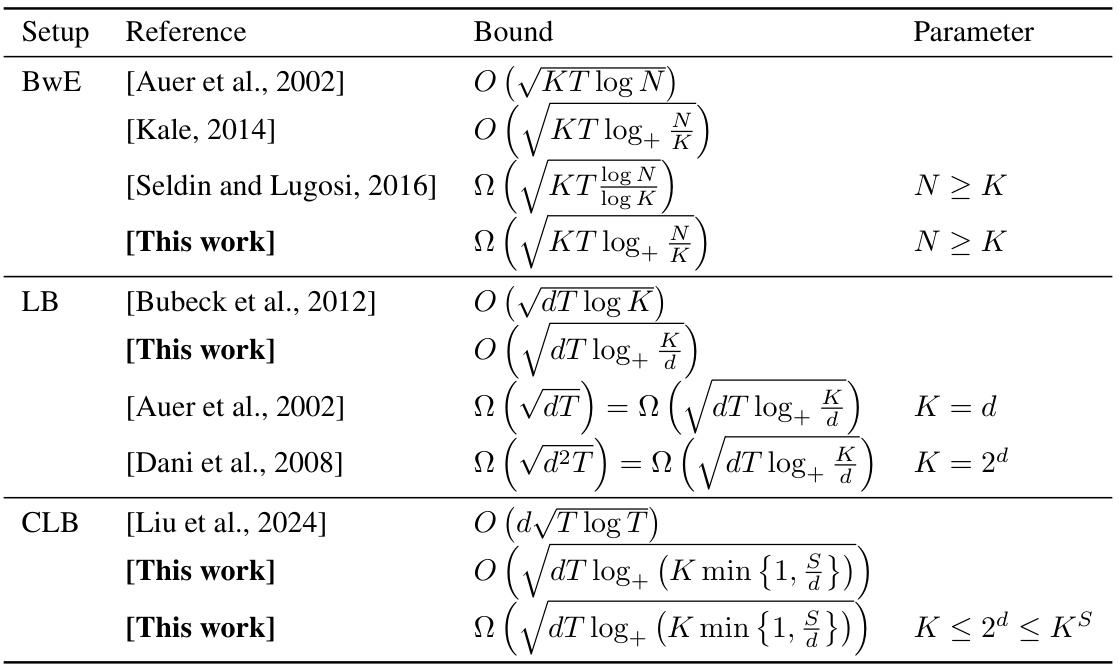
This table summarizes the upper and lower bounds on the minimax regret for three different multi-armed bandit problems: multi-armed bandits with expert advice (BwE), linear bandits (LB), and contextual linear bandits (CLB). For each problem, it shows the regret bounds achieved by previous work and the current paper. The parameters K (number of arms), N (number of experts), d (dimensionality of feature vectors), and S (size of context space) are also defined.
Full paper#



















