↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Probabilistic inference, crucial in various fields, faces challenges with high-dimensional and multimodal distributions. Existing methods like MCMC often struggle with slow mixing times and getting stuck in local modes. Variational inference (VI) methods using normalizing flows offer an alternative but typically involve expensive training procedures. This work addresses these limitations.
The proposed Markovian Flow Matching (MFM) method cleverly integrates continuous normalizing flows (CNFs) with adaptive Markov chain Monte Carlo (MCMC) sampling. MFM uses a simulation-free training objective for the CNF, significantly improving efficiency. An adaptive tempering mechanism is incorporated to effectively explore multimodal distributions. The authors establish convergence of the method to a local optimum under certain assumptions, showcasing its robustness. Experiments demonstrate comparable performance to state-of-the-art methods, often at a substantially lower computational cost.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel and efficient method for probabilistic inference, a crucial problem in various fields. The method combines the power of continuous normalizing flows (CNFs) with adaptive Markov Chain Monte Carlo (MCMC) sampling, offering a significant advancement over existing techniques. Its simulation-free training, scalability, and convergence properties make it highly relevant to researchers working on complex probability distributions. Furthermore, the adaptive tempering mechanism and theoretical analysis of convergence make it especially useful for complex multimodal distributions.
Visual Insights#

This figure compares the performance of four different sampling methods on a 4-mode Gaussian mixture. MFM (Markovian Flow Matching), FAB (Flow Annealed Importance Sampling Bootstrap), DDS (Denoising Diffusion Sampler), and NF-MCMC (Adaptive Monte Carlo with Normalizing Flows) are compared. The plot shows samples generated by each method overlaid on the true density contours, visualizing how well each method captures the multimodality of the target distribution. The figure highlights MFM’s ability to effectively sample from all four modes, while others show limitations in capturing all the modes.
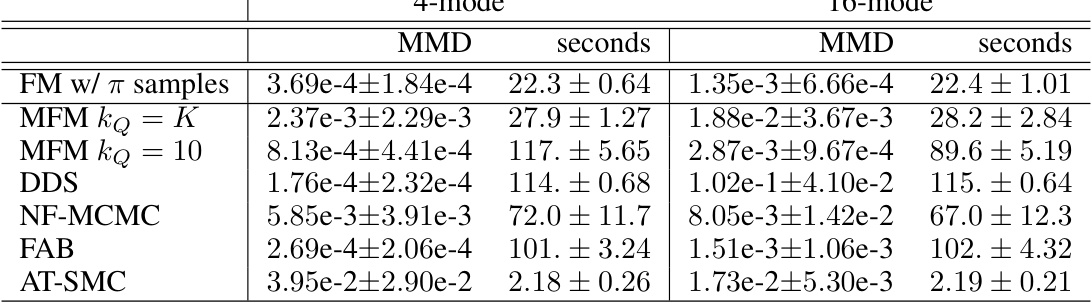
This table presents the Maximum Mean Discrepancy (MMD) and computation time for different methods on two synthetic datasets: a 4-mode Gaussian mixture and a 16-mode Gaussian mixture. The MMD measures the difference between samples generated by each method and true samples from the target distribution. Lower MMD values indicate better performance. The results show that the proposed method (MFM) achieves similar performance to state-of-the-art methods but often with significantly lower computational cost.
In-depth insights#
Markovian Flow Match#
Markovian Flow Matching proposes a novel approach to probabilistic inference by cleverly combining continuous normalizing flows (CNFs) with adaptive Markov Chain Monte Carlo (MCMC) methods. The core idea is to leverage CNFs to learn the probability path between a simple reference distribution and the target distribution, enabling the creation of flow-informed transition kernels within an MCMC sampler. This contrasts with traditional MCMC algorithms, which often struggle with high-dimensional, multimodal targets. By incorporating a flow-informed kernel alongside a local kernel (like MALA), Markovian Flow Matching aims to improve exploration efficiency and convergence. The adaptive nature of the algorithm is crucial, as the CNF parameters and tempering schedule are updated on-the-fly, allowing the method to handle complex distributions and to discover multiple modes. Theoretical convergence guarantees are provided under mild assumptions, demonstrating the method’s robustness. Experimental results on both synthetic and real-world data suggest that Markovian Flow Matching offers comparable performance to state-of-the-art methods, often at significantly lower computational cost.
Adaptive MCMC#
Adaptive Markov Chain Monte Carlo (MCMC) methods are crucial for efficiently sampling from complex, high-dimensional probability distributions. Standard MCMC algorithms often struggle with slow mixing times, especially in multimodal scenarios. Adaptive MCMC addresses this by dynamically adjusting the proposal distribution or other algorithm parameters based on the samples collected during the process. This allows the algorithm to learn the target distribution’s characteristics, improving exploration and convergence. Key aspects include mechanisms for updating parameters, such as using gradient-based optimization, and ensuring that the adaptive process does not disrupt the convergence guarantees of the underlying MCMC method. Careful consideration of the update rules and the frequency of adaptation is essential for efficient and robust performance. The use of continuous normalizing flows integrated into an adaptive MCMC scheme is a significant advancement, offering a powerful method for learning the probability path and efficiently generating samples from challenging distributions. This approach not only improves the exploration of complex target distributions but also potentially reduces computational cost. However, challenges remain in balancing the adaptive updates and choosing appropriate proposal distributions. The convergence and efficiency are sensitive to choices made in designing adaptive strategies.
CNF Training#
Training continuous normalizing flows (CNFs) effectively is crucial for their success in probabilistic inference. Standard maximum likelihood estimation is computationally expensive, particularly for high-dimensional targets. Flow matching (FM) offers a compelling alternative, avoiding the need for likelihood calculations and instead directly minimizing the discrepancy between the CNF’s generated vector field and the target’s. The adaptive nature of the proposed algorithm dynamically adjusts the CNF based on samples obtained from Markov chain Monte Carlo (MCMC), further enhancing efficiency. However, FM’s success relies on obtaining adequate samples from the MCMC chain. Convergence is guaranteed to a local optimum under specified assumptions, yet this local optimum might not be globally optimal, implying possible limitations if the target distribution is highly multimodal. The choice of the reference distribution is another critical factor and may influence performance. Finally, adaptive tempering strategies are critical in handling multi-modal targets, where an annealing approach can facilitate exploration of various modes and avoid getting stuck in local optima, which is particularly important in high-dimensional scenarios.
Experimental Results#
The experimental results section of a research paper is crucial for validating the claims and demonstrating the effectiveness of proposed methods. A strong results section will clearly present the findings using appropriate visualizations (e.g., tables, graphs) and metrics. The choice of metrics should be justified and relevant to the research questions. The results should be presented comprehensively, showing both successes and potential limitations, and any unexpected findings should be discussed. A comparison to existing state-of-the-art methods is vital for establishing the novelty and impact of the work. Finally, a thorough analysis of the results is essential for drawing meaningful conclusions and providing insights into the practical implications of the study. Transparency and reproducibility are key; detailed descriptions of experimental setups and parameters must be provided to facilitate verification of the findings by other researchers.
Future Work#
The paper’s ‘Future Work’ section could explore several avenues to enhance the Markovian Flow Matching (MFM) method. Improving theoretical guarantees beyond local convergence is crucial. Investigating non-asymptotic convergence rates would provide a more complete understanding of the method’s performance. The impact of different CNF architectures on MFM’s efficacy requires further analysis. Tailoring CNFs to specific posterior distributions, rather than using a generic architecture, could significantly improve the method’s performance on complex problems. Developing adaptive schemes for hyperparameters such as the number of local MCMC steps before a global step would automate the process and improve robustness. Finally, exploring applications to high-dimensional real-world problems where the computational efficiency of MFM becomes particularly valuable will demonstrate its practical applicability and scalability.
More visual insights#
More on figures
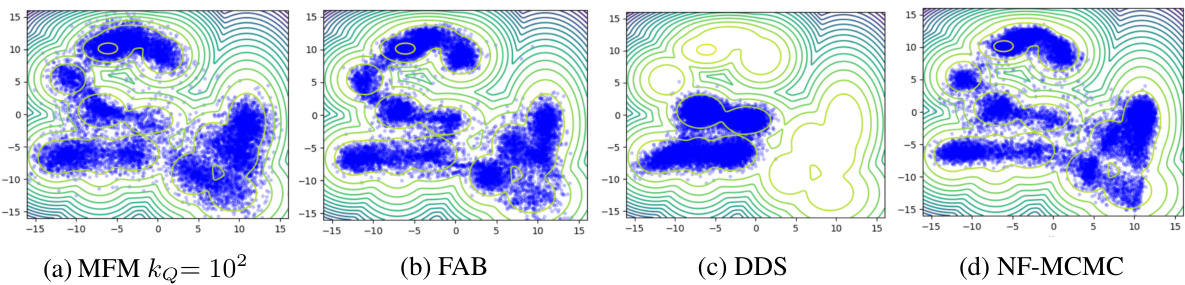
This figure compares the performance of four different sampling methods: Markovian Flow Matching (MFM), Flow Annealed Importance Sampling Bootstrap (FAB), Denoising Diffusion Sampler (DDS), and Adaptive Monte Carlo with Normalizing Flows (NF-MCMC) on a 4-mode Gaussian mixture. The figure shows scatter plots of samples generated by each method, overlaid on contour lines representing the true target density. The plots visually demonstrate how well each method captures the four modes of the distribution. MFM and DDS perform best in capturing all the modes, while FAB and NF-MCMC struggle.
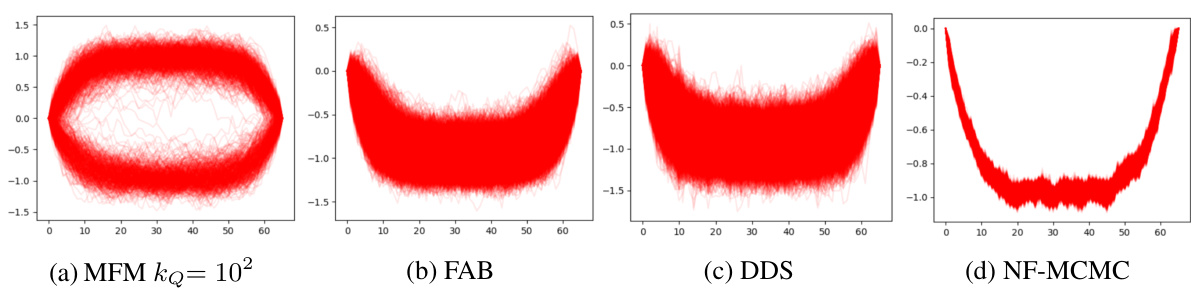
This figure compares the samples generated by four different methods for approximating a 4-mode Gaussian mixture distribution. The methods compared are Markovian Flow Matching (MFM), Flow Annealed Importance Sampling Bootstrap (FAB), Denoising Diffusion Sampler (DDS), and Adaptive Monte Carlo with Normalizing Flows (NF-MCMC). Each subplot shows a scatter plot of the samples generated by a particular method, illustrating their ability to capture the four distinct modes of the target distribution. Visually comparing the plots helps to assess the relative strengths and weaknesses of the different methods in accurately representing the target distribution.
More on tables

This table presents the results of the Maximum Mean Discrepancy (MMD) and computation time for four different methods and two synthetic datasets. The MMD measures the difference between samples from the true distribution and samples generated from a learned continuous normalizing flow (CNF). Lower MMD values indicate a better approximation of the true distribution. The results are averaged over 10 independent runs, and 95% confidence intervals are provided.
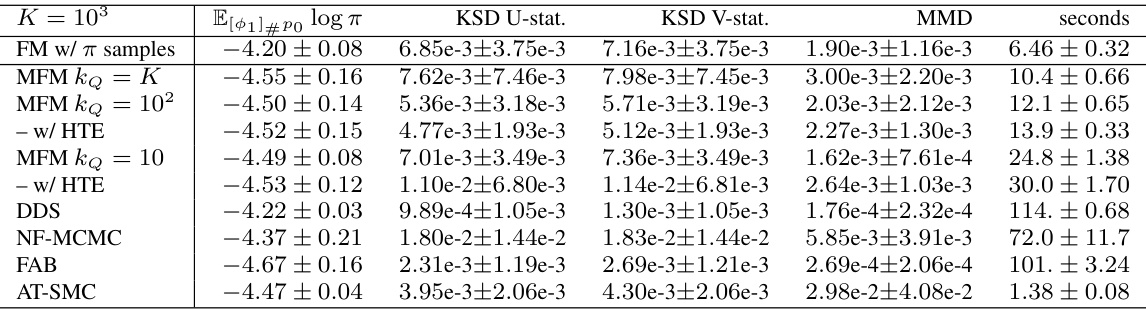
This table presents the results of the Maximum Mean Discrepancy (MMD) and computation time for four different methods (FM w/ π samples, MFM kQ = K, MFM kQ = 10, DDS, NF-MCMC, FAB, AT-SMC) applied to two synthetic datasets: a 4-mode Gaussian mixture and a 16-mode Gaussian mixture. The MMD measures the discrepancy between the generated samples and the true target distribution, while the computation time reflects the efficiency of each method. The results are averaged across 10 independent runs with 95% confidence intervals.
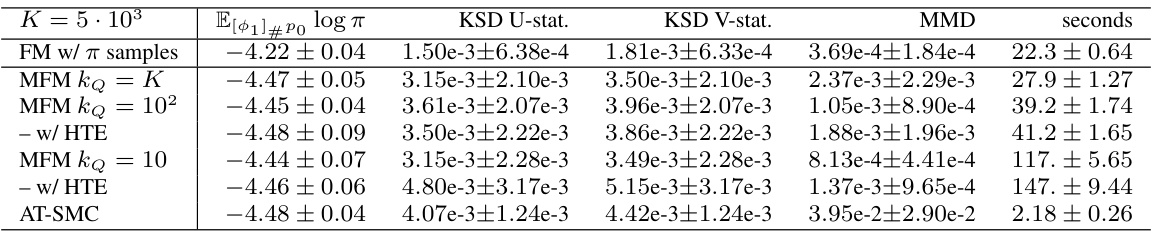
This table presents the results of the Maximum Mean Discrepancy (MMD) and the computation time for four different methods (FM w/ π samples, MFM with different values of kQ, DDS, NF-MCMC, FAB, and AT-SMC) applied to two synthetic datasets (4-mode and 16-mode Gaussian mixtures). The MMD metric measures the difference between the generated samples and the true target distribution. Lower MMD values indicate a better approximation of the target distribution. The computation time provides a measure of the efficiency of each method. The results are averaged over ten independent runs, and 95% confidence intervals are reported.

This table presents the results of the Maximum Mean Discrepancy (MMD) and computation time for various methods on two synthetic datasets (4-mode and 16-mode Gaussian mixtures). The MMD measures how well the samples generated by each method approximate the true target distribution. Lower MMD values indicate better approximations. The table includes results for the proposed Markovian Flow Matching (MFM) method and several baselines, along with confidence intervals.

This table presents the results of applying different algorithms to two synthetic datasets: a 4-mode Gaussian Mixture and a 16-mode Gaussian Mixture. For each dataset and algorithm, the table shows the Maximum Mean Discrepancy (MMD), a measure of how well the samples generated by the algorithm match the true target distribution, as well as the computation time in seconds. The MMD values are averaged over 10 independent runs, along with their 95% confidence intervals, providing a measure of the variability in the results.

This table presents the results of two synthetic experiments. The Maximum Mean Discrepancy (MMD) metric quantifies the difference between samples from the true target distribution and samples generated by the learned continuous normalizing flow (CNF). The table shows the MMD values, computation times in seconds, and 95% confidence intervals across 10 independent runs for several different methods, including Markovian Flow Matching (MFM) and other state-of-the-art methods.

This table presents the results of two synthetic experiments, a 4-mode and a 16-mode Gaussian mixture. For each experiment, the Maximum Mean Discrepancy (MMD) is calculated, measuring the difference between samples generated by the learned flow and true samples from the target distribution. The results (MMD and computation time) are averaged across ten independent runs, and 95% confidence intervals are provided.

This table presents the results of applying several methods to two real-world datasets: the Field system and the Log-Gaussian Cox process. The performance is evaluated using the Kernel Stein Discrepancy (KSD) which measures the difference between the target distribution and the samples generated using the learned flow. Both U-statistic and V-statistic values are provided. The computation time is also reported, highlighting the relative efficiency of each method. Results are averaged over 10 independent runs, with 95% confidence intervals reported.

This table presents the Maximum Mean Discrepancy (MMD) and computation time for different methods on two synthetic datasets: a 4-mode Gaussian mixture and a 16-mode Gaussian mixture. The MMD measures how well the samples generated by each method match the true target distribution. Lower MMD values indicate better performance. The table also shows the time taken for each method to generate the samples.
Full paper#