↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Diffusion models excel in generating high-quality outputs but suffer from slow sampling speeds due to the numerous steps involved. Existing acceleration techniques, while showing some promise, often need extensive fine-tuning, limiting their practicality. This high computational cost stems from the mismatch between fine-tuning steps and sampling steps, as well as complex optimization objectives.
Simple and Fast Distillation (SFD) tackles these issues with a simplified approach. By focusing on fine-tuning a small number of crucial timestamps, and by addressing other efficiency-boosting factors, SFD achieves a substantial 1000x reduction in training time compared to existing methods. SFD also introduces variable-NFE sampling, enhancing flexibility. Experimental results confirm SFD’s efficiency, generating high-quality images with only a fraction of the usual training time and cost.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on generative models because it offers a significantly faster and more efficient method for training diffusion models. The speed improvement of 1000x in fine-tuning time is groundbreaking and directly addresses a major bottleneck in the field. This breakthrough enables broader adoption of diffusion models in various applications, especially those with limited resources or time constraints. Furthermore, the introduction of variable-NFE sampling opens new avenues for model optimization and exploration.
Visual Insights#

This figure compares different diffusion model acceleration methods based on their FID (Fréchet Inception Distance) scores and fine-tuning time (in A100 GPU hours). It highlights that the proposed SFD method (Simple and Fast Distillation) achieves state-of-the-art performance with significantly less fine-tuning time compared to existing methods. The x-axis represents the fine-tuning time, and the y-axis represents the FID score. Lower FID values indicate better image generation quality, and shorter fine-tuning times indicate higher efficiency. The chart is divided into solver-based and distillation-based methods, with SFD falling into the latter and outperforming other distillation methods.
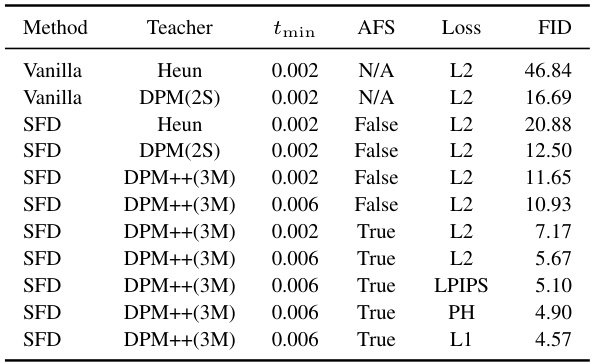
This table presents a quantitative comparison of different ablation studies performed on the proposed Simple and Fast Distillation (SFD) method. The ablations cover various aspects of the method, including the choice of teacher solver, minimum timestamp (tmin), the use of Analytical First Step (AFS), and the loss function used during training. The results are measured in terms of the Fréchet Inception Distance (FID), a common metric for evaluating the quality of generated images. Lower FID scores indicate better image quality. The table allows readers to assess the impact of each design choice on the overall performance of the SFD method.
In-depth insights#
Diffusion Model Speedup#
Diffusion models, while powerful, suffer from slow sampling speeds. Speedup techniques are crucial for practical applications and several methods exist to address this. Solver-based approaches leverage numerical methods to accelerate sampling, but often compromise sample quality at lower function evaluations (NFEs). Distillation-based methods, in contrast, aim to create a simplified, faster “student” model by learning from a slower but higher-quality “teacher” model. These methods offer a trade-off between speed and quality, but often require extensive, time-consuming fine-tuning. Recent research focuses on simplifying distillation, streamlining the training process, and achieving variable NFE sampling with a single model to improve efficiency and address the practical limitations of existing techniques. The key is to find the balance between sample quality, training efficiency, and the flexibility to adjust the sampling process for different speed/quality requirements.
SFD: A Novel Approach#
The heading “SFD: A Novel Approach” suggests a research paper introducing a new method called SFD. A thoughtful analysis would anticipate that the paper details SFD’s design, showcasing its innovation and improvements over existing methods. It likely presents a comprehensive evaluation, comparing SFD’s performance to state-of-the-art techniques using various metrics like accuracy and efficiency. The novelty of SFD would be a central focus, emphasizing its unique features and mechanisms. A deeper examination would explore the theoretical underpinnings of SFD, explaining its principles and how it functions. The practical applications and limitations of SFD are also critical components, presenting realistic scenarios where the method can be effectively used, and providing insights into scenarios where it falls short. Finally, the paper’s conclusion should summarize the key contributions of SFD, suggesting potential future research directions based on its findings.
Ablation Studies#
Ablation studies systematically remove components of a model or process to understand their individual contributions. In the context of a research paper, this would involve a series of experiments where a specific aspect is altered or removed, allowing the researcher to isolate its impact on overall performance. This might involve removing hyperparameters, modifying parts of an algorithm, or testing different model architectures. The goal is to demonstrate the necessity and effectiveness of each included part. Well-conducted ablation studies provide strong evidence for design choices, ruling out alternative explanations for success, and highlighting which features are truly essential for achieving the desired results. A thorough ablation study is crucial for establishing the validity and robustness of a research claim. The results are often presented in a tabular or graphical format, showing a clear comparison of performance metrics under different conditions. They are a critical aspect of any rigorous empirical evaluation.
Variable-NFE Sampling#
Variable-NFE sampling in diffusion models addresses a critical limitation: the fixed number of sampling steps. Traditional methods require a pre-defined number of steps, limiting their flexibility and efficiency. Variable-NFE sampling overcomes this by allowing the model to adapt the number of steps needed based on the input or desired output quality. This adaptability is achieved through various techniques, including conditional models that incorporate step information into the process or by modifying the model’s dynamics to enable varying step counts. Benefits include improved efficiency by reducing unnecessary computations when fewer steps suffice and enhanced control over the quality-speed trade-off. However, challenges exist in designing effective variable-NFE models, including managing the complexity of handling variable-length sequences and potentially impacting the model’s training and inference stability. Further research is needed to fully explore the potential and address the challenges of variable-NFE sampling in diffusion models, particularly concerning the optimization strategies and model architectures needed to achieve optimal performance and scalability.
Future Work#
The paper’s exploration of simple and fast distillation for diffusion models opens several exciting avenues for future research. Improving the FID scores to match or exceed state-of-the-art methods is a primary goal. This likely involves a deeper investigation of the underlying geometric structure of diffusion models, potentially leading to more effective time schedules or model architectures. Expanding the application beyond image generation to other modalities like video, audio, and 3D models would demonstrate broader utility. Addressing the mismatch between fine-tuning and sampling steps more effectively is also crucial. A more comprehensive analysis of the effect of different hyperparameters and optimization objectives could refine SFD and further enhance its efficiency. Finally, thorough exploration of the variable-NFE model (SFD-v) to ensure robustness and optimal performance across various step sizes is a priority. Further investigation into potential ethical concerns surrounding generative models and developing safeguards are necessary for responsible deployment.
More visual insights#
More on figures

This figure compares different diffusion model acceleration methods based on their FID score (a measure of image quality) and fine-tuning time. The x-axis represents the fine-tuning time on a single NVIDIA A100 GPU, and the y-axis represents the FID score achieved by the method at a specified number of function evaluations (NFEs). The figure demonstrates that the proposed method (SFD) achieves state-of-the-art performance with significantly reduced fine-tuning time compared to other methods.
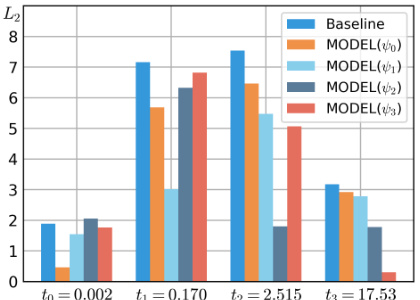
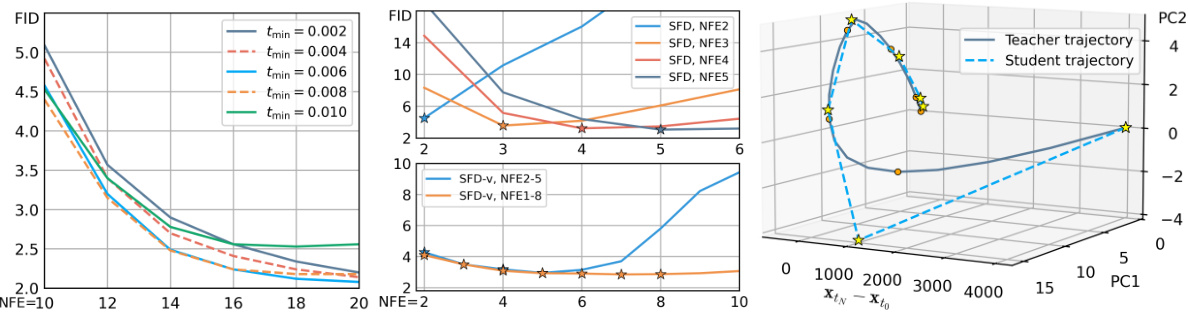
This figure shows the results of an ablation study to validate the strategy of fine-tuning only a few timestamps that will be used in sampling. Four different student models are initialized from a pre-trained teacher model and fine-tuned only on a certain timestamp. The L2 distance between the teacher and student model sampling trajectory is calculated and visualized for all timestamps. The results demonstrate that fine-tuning at a specific timestamp can positively impact the gradient direction at other timestamps, even though they are far apart, which means that fine-tuning on a fine-grained time schedule is unnecessary.

This figure compares different diffusion model acceleration methods based on their FID score (a measure of image quality) and fine-tuning time. It highlights that the proposed SFD method (marked with a star) achieves state-of-the-art FID scores while requiring significantly less fine-tuning time than other methods. The x-axis is the fine-tuning time on a single NVIDIA A100 GPU (in hours), and the y-axis is the FID score. The chart distinguishes between solver-based and distillation-based methods, illustrating the superior efficiency of the proposed SFD approach.
This figure compares various diffusion model acceleration methods based on their FID score (a measure of image generation quality) and fine-tuning time on a single NVIDIA A100 GPU. It shows that the proposed SFD method achieves state-of-the-art performance with significantly reduced fine-tuning time compared to other methods. The x-axis is a log scale representing the fine-tuning time in hours, while the y-axis represents the FID score. The different markers represent different acceleration methods, categorized as solver-based or distillation-based methods. The figure highlights the superior performance and efficiency of the SFD approach.

This ablation study compares the performance of two different conditioning methods used in the SFD-v model for variable-NFE distillation. The graph shows the FID scores over training iterations for both the ’tnext-cond’ (next time step condition) and ‘step-cond’ (step condition) approaches, each tested at different numbers of function evaluations (NFEs). The results indicate that the ‘step-cond’ approach generally performs better than ’tnext-cond’ in achieving lower FID scores across various NFEs, demonstrating its superior effectiveness for variable-step sampling.

This figure compares various acceleration methods for diffusion models based on their FID score and fine-tuning time on a single NVIDIA A100 GPU. It highlights the trade-off between achieving a low FID (indicating high-quality image generation) and the time required for fine-tuning a model. The authors’ method (SFD) is shown to achieve state-of-the-art FID scores with significantly reduced fine-tuning times compared to other methods, emphasizing its efficiency.

This ablation study compares different loss functions (L1, L1 + LPIPS) and training approaches (single-stage SFD, two-stage SFD) for one-NFE distillation. The y-axis represents the FID score, a measure of image quality, and the x-axis shows the number of training iterations. The results illustrate the impact of the loss function and the benefit of the second stage of training on improving the quality of images generated with only one step in the sampling process.

The figure compares various acceleration methods for diffusion models based on the fine-tuning time and FID score (Fréchet Inception Distance) at different numbers of function evaluations (NFEs). It shows that the proposed method (SFD) achieves state-of-the-art performance with significantly reduced fine-tuning time compared to other methods, highlighting its efficiency and effectiveness in accelerating diffusion model sampling.

The figure compares different acceleration methods for diffusion models in terms of FID (Fréchet Inception Distance) score and fine-tuning time. It shows that the proposed SFD method (Simple and Fast Distillation) achieves state-of-the-art performance with significantly reduced fine-tuning time compared to other methods.

The figure shows a comparison of different diffusion model acceleration methods, plotting the FID score against the fine-tuning time required on a single NVIDIA A100 GPU. The x-axis is fine-tuning time (in hours, shifted for better visualization), and the y-axis is the Fréchet Inception Distance (FID), a measure of image quality. Various methods are represented, categorized into solver-based and distillation-based approaches. The figure highlights that the proposed SFD method achieves state-of-the-art FID scores with significantly lower fine-tuning time compared to other methods.

The figure compares different acceleration methods for diffusion models based on the FID score and the fine-tuning time required. It shows that the proposed method (SFD) achieves state-of-the-art performance with significantly less fine-tuning time compared to other methods. The x-axis is the fine-tuning time (in hours on a single NVIDIA A100 GPU), and the y-axis is the FID score, a measure of image generation quality. Lower FID indicates better quality. The chart highlights that SFD achieves a good balance between sample quality and the cost of fine-tuning.

The figure compares various acceleration methods for diffusion models in terms of their final FID score and the time it took to fine-tune the models. It highlights that the proposed SFD method (Simple and Fast Distillation) achieves state-of-the-art performance with significantly less fine-tuning time compared to other methods. The y-axis represents the final FID score (lower is better), while the x-axis shows the fine-tuning time in hours on a single NVIDIA A100 GPU. The figure uses a log scale for the x-axis to better visualize the large differences in fine-tuning times.
The figure compares different acceleration methods for diffusion models in terms of FID score and fine-tuning time. It highlights that the proposed SFD method achieves state-of-the-art performance with significantly lower fine-tuning time compared to other methods.

This figure compares various diffusion model acceleration methods based on their FID score and fine-tuning time. It highlights that the proposed SFD method (shown as ★) achieves state-of-the-art FID scores (a measure of image quality) with significantly lower fine-tuning time (approximately 1000x faster) compared to other methods. The x-axis is the fine-tuning time (in hours) on an NVIDIA A100 GPU, and the y-axis represents the FID score. The figure emphasizes SFD’s efficiency in achieving high-quality image generation at a fraction of the computational cost.

This figure compares various acceleration methods for diffusion models based on the Fine-tuning time (in A100 hours) against the FID score (a measure of image quality). It highlights that the proposed SFD method achieves state-of-the-art performance with significantly reduced fine-tuning time compared to other methods. The x-axis is a log scale.
More on tables
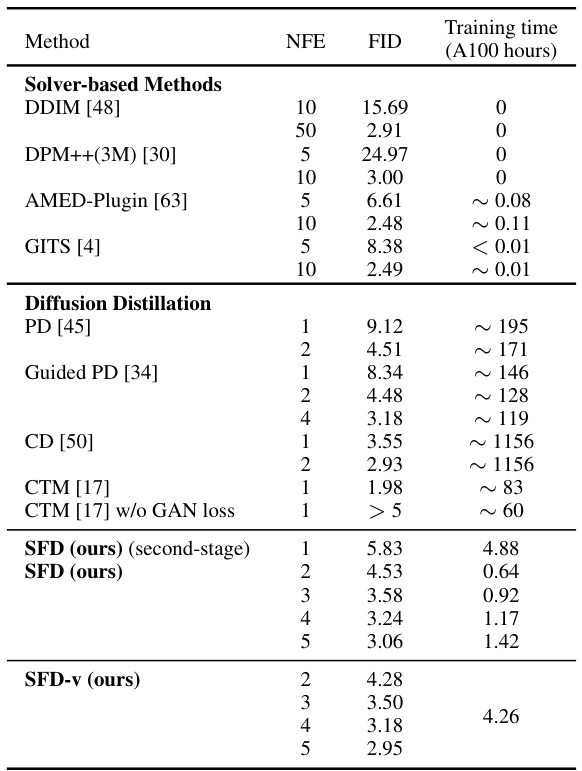
This table presents a comparison of different diffusion models and methods on the CIFAR-10 dataset with image size 32x32. It shows the FID (Fréchet Inception Distance) score, the number of function evaluations (NFEs), and the training time (in A100 GPU hours) for each method. The methods are categorized into solver-based methods and diffusion distillation methods, allowing for a direct comparison of performance and efficiency.
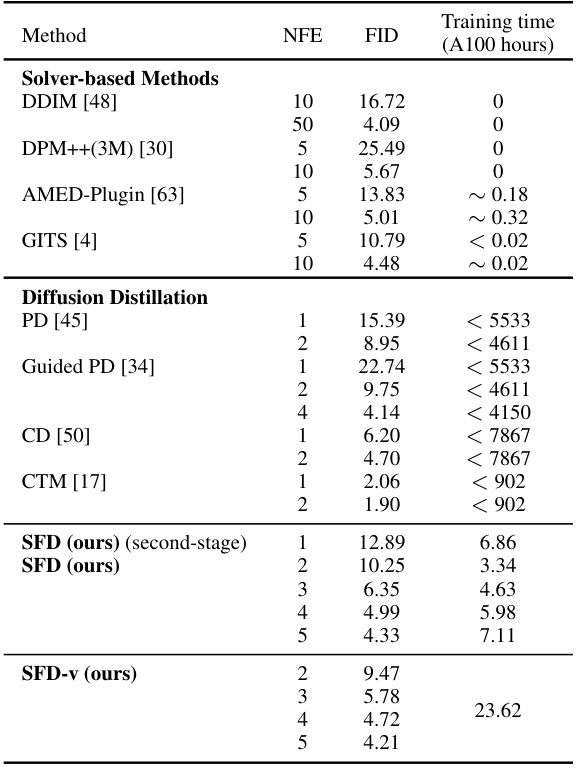
This table presents a comparison of different diffusion models’ performance on the CIFAR-10 dataset. It shows the FID (Fréchet Inception Distance) scores achieved by various methods, categorized as solver-based and diffusion distillation methods. The number of function evaluations (NFEs) and the training time (in A100 GPU hours) are also listed for each method. This allows for a comparison of both sample quality and computational cost.
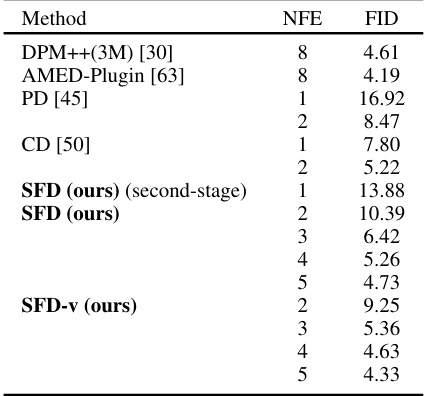
This table presents a comparison of different methods’ FID scores on the LSUN-Bedroom dataset, with images of size 256x256. The methods compared include DPM++(3M), AMED-Plugin, Progressive Distillation (PD), Consistency Distillation (CD), and the proposed SFD and SFD-v methods. The Number of Function Evaluations (NFE) is also provided for each method, indicating the computational cost of generating samples.
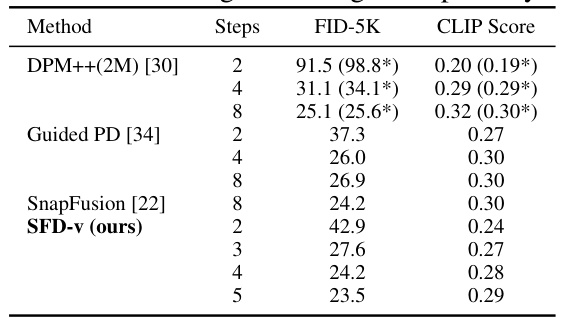
This table presents the quantitative results of text-to-image generation using Stable Diffusion. It compares the FID (Fréchet Inception Distance) and CLIP score of different methods at varying numbers of sampling steps. The results are obtained using a guidance scale of 7.5, which is the default setting in the original Stable Diffusion repository. The table provides a comparison between the authors’ method (SFD-v) and existing methods such as DPM++(2M) and Guided PD, illustrating the performance of SFD-v in terms of image quality and alignment with text prompts.

This table presents the FID scores and training times (in A100 hours) for various methods on the CIFAR10 dataset. It compares solver-based methods (DDIM, DPM++(3M), AMED-Plugin, GITS) with diffusion distillation methods (PD, Guided PD, CD, CTM, CTM w/o GAN loss, SFD, SFD-v), showcasing the efficiency of SFD and SFD-v in achieving comparable FID scores with significantly less training time.
This table presents the quantitative results of different diffusion models on the CIFAR10 dataset, specifically focusing on the Fréchet Inception Distance (FID) and training time on a single NVIDIA A100 GPU. It compares solver-based methods (DDIM, DPM++(3M), AMED-Plugin, GITS) and diffusion distillation methods (PD, Guided PD, CD, CTM, SFD, and SFD-v), demonstrating the efficiency and effectiveness of the proposed SFD method.
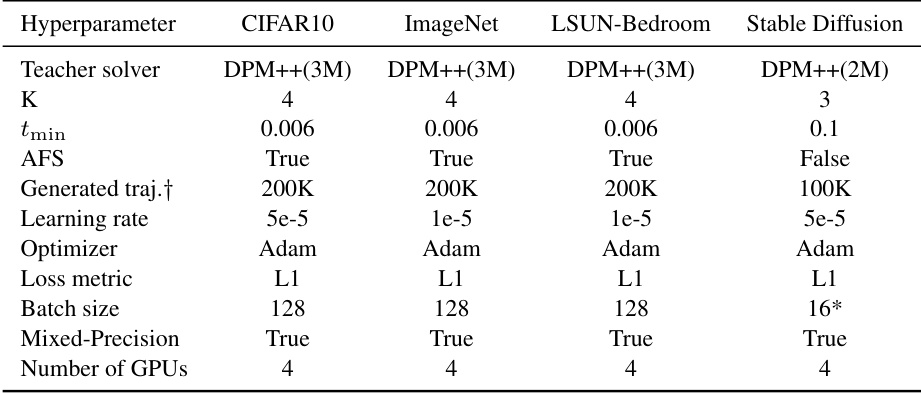
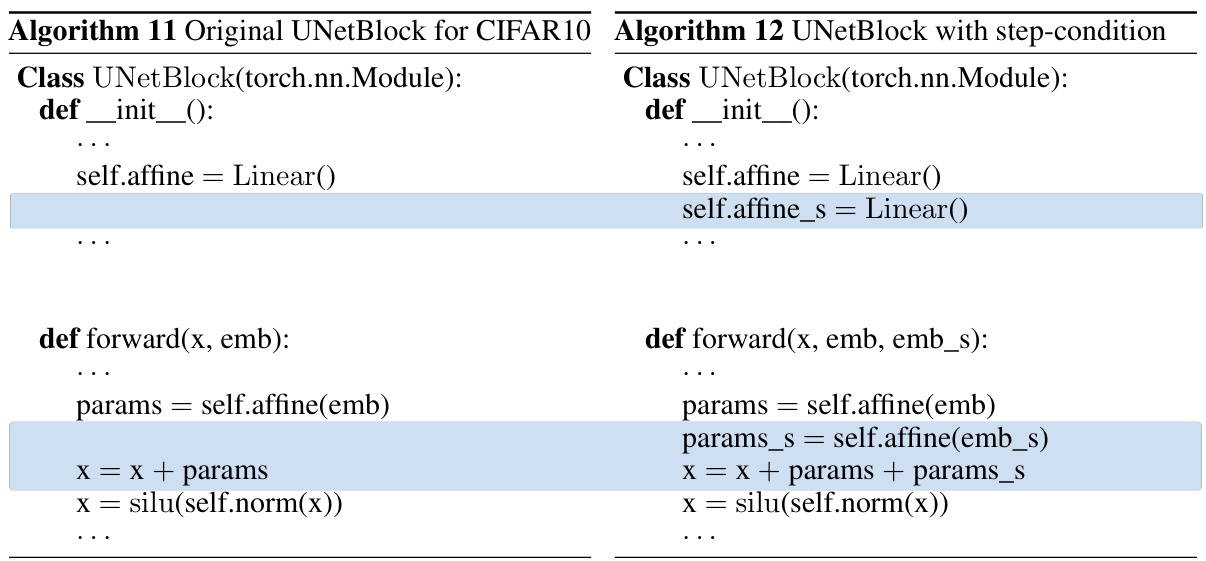
This table lists the hyperparameters used for training the models on the four datasets (CIFAR10, ImageNet, LSUN-Bedroom, and Stable Diffusion). The table specifies the teacher solver, the number of teacher sampling steps (K), the minimum timestamp (tmin), whether analytical first step (AFS) was used, the number of generated teacher trajectories, the learning rate, the optimizer, the loss metric, the batch size, whether mixed precision was used, and the number of GPUs used. Note that some values differ slightly depending on the dataset due to specific requirements and optimization strategies.

This table shows the FID scores achieved by different methods on the CIFAR-10 dataset. The methods compared include the proposed SFD and its variant SFD-v, along with baselines. Different numbers of function evaluations (NFEs) are tested. The gray rows highlight results explicitly discussed in the main paper, while the second-stage refers to a further distillation step applied to SFD. The SFD-v results indicate different lengths of the list of sampling steps used in the algorithm.

This table presents the results of an ablation study conducted to determine the optimal number of teacher sampling steps (K) for the Simple and Fast Distillation (SFD) method on the CIFAR-10 dataset. The study varied K (from 1 to 6) while keeping other hyperparameters consistent. The table shows the resulting Fréchet Inception Distance (FID) scores and the corresponding fine-tuning time (in hours) on a single NVIDIA A100 GPU for different numbers of function evaluations (NFEs), ranging from 2 to 5. Lower FID scores indicate better image generation quality, and shorter fine-tuning times represent greater computational efficiency. The results help in selecting the most effective value of K for the SFD method.

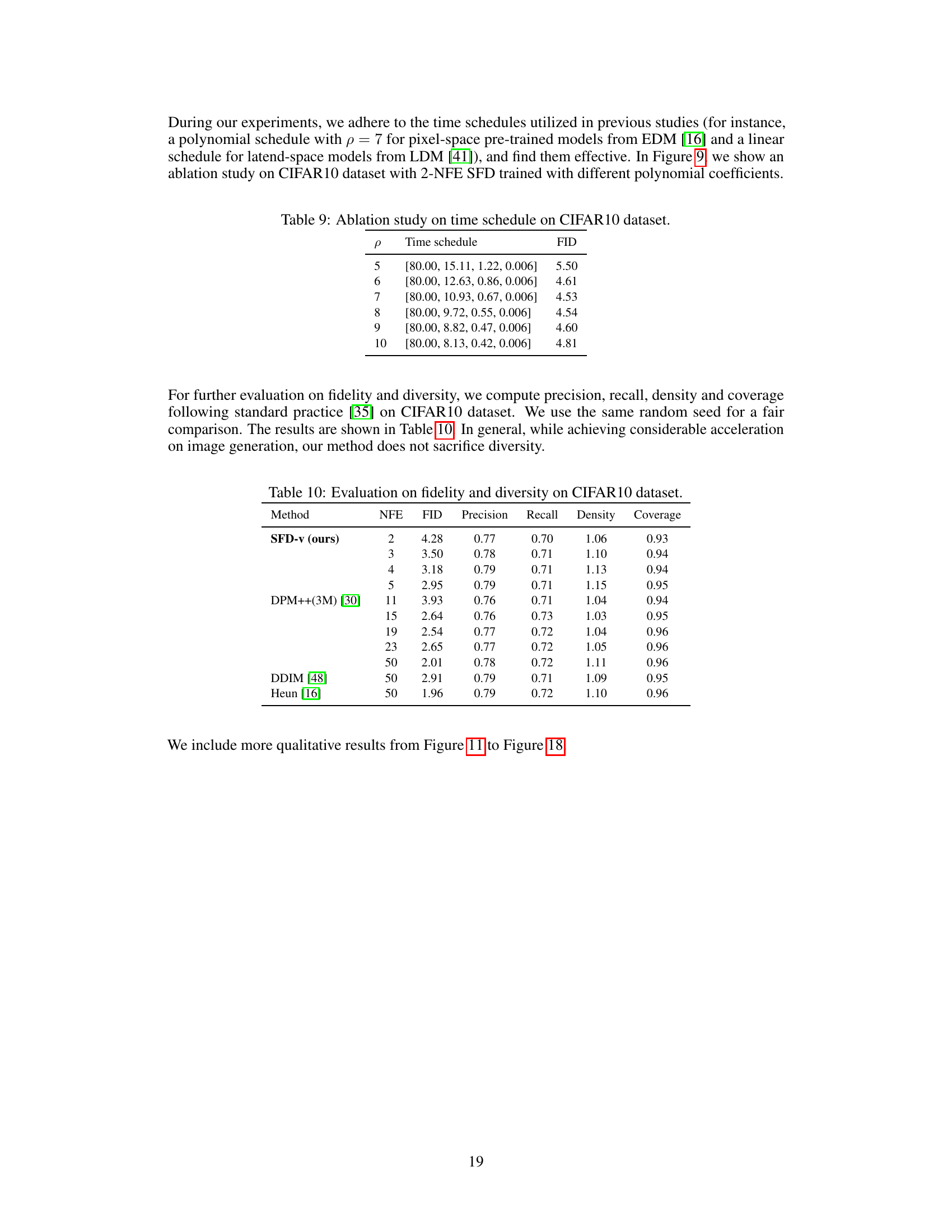
This table presents the results of an ablation study conducted on the CIFAR-10 dataset to evaluate the impact of different time schedules on the performance of the proposed method. The study varied the polynomial coefficient (ρ) used in generating the time schedule, resulting in different FID scores (Fréchet Inception Distance). The FID score is a metric used to evaluate the quality of generated images, with lower scores indicating better quality. The table shows that a polynomial coefficient of 7 provides the best FID score (4.53), indicating that this particular time schedule yields the highest-quality images.

This table presents a quantitative comparison of the proposed SFD-v method with existing methods (DPM++(3M) [30], DDIM [48], and Heun [16]) in terms of fidelity and diversity on the CIFAR10 dataset. Fidelity and diversity are important aspects of evaluating the quality of generated images. The metrics used to assess fidelity include precision, recall, density and coverage. The NFE (Number of Function Evaluations) column indicates the computational cost involved in generating each sample. The results highlight that SFD-v achieves competitive FID scores while maintaining comparable diversity to existing methods. This demonstrates the effectiveness of the proposed method for high-quality image generation with reduced computational cost.
Full paper#