Differentially Private Graph Diffusion with Applications in Personalized PageRanks

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with sensitive graph data. It offers a novel framework for achieving edge-level differential privacy in graph diffusion, a critical area with significant implications for various applications. The proposed method, which uses a novel ∞-Wasserstein distance tracking approach, improves the utility-privacy tradeoff, providing a practical and effective solution for privacy-preserving graph analysis and computation.

Visual Insights

#

This figure demonstrates how the distortion introduced by edge perturbation varies depending on the degree of the nodes involved. In the left panel, a low-degree node is perturbed resulting in a larger distortion (0.7) compared to when a high-degree node is perturbed in the right panel (0.525). The difference in distortion highlights the impact of degree on the algorithm’s sensitivity.

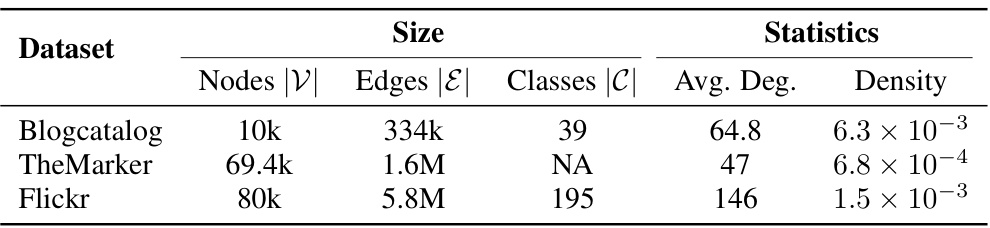
This table presents the characteristics of three real-world benchmark datasets used in the paper’s experiments: BlogCatalog, TheMarker, and Flickr. For each dataset, it provides the number of nodes (|V|), the number of edges (|E|), the number of classes (|C|), the average degree, and the network density. The statistics help to characterize the size and structure of each network, which is important for understanding the results of the privacy-preserving graph diffusion experiments.

In-depth insights

#

Private Graph Diffusion

#

Private graph diffusion tackles the challenge of analyzing graph data while preserving user privacy. Traditional graph diffusion methods, while powerful for tasks like PageRank calculation, risk revealing sensitive information about the relationships encoded in the graph. This privacy concern necessitates innovative techniques that incorporate differential privacy or other privacy-preserving mechanisms to mask individual connections. Noisy graph diffusion, where noise is added during iterative diffusion computations, is a common approach, but careful tuning is critical to balance privacy guarantees with the utility of the analysis. Edge-level differential privacy offers a robust approach, focusing on ensuring that altering a single edge has a minimal impact on the output, protecting the privacy of individual relationships. However, the interconnected nature of graphs makes it challenging to prevent information leakage from the perturbed data, and methods need to address the high sensitivity of low-degree nodes to edge modifications. Research in private graph diffusion focuses on developing and analyzing these privacy-preserving algorithms, including their theoretical guarantees and their efficacy in real-world scenarios.

PABI in Graph Diff

#

The application of Privacy Amplification by Iteration (PABI) to graph diffusion presents a novel approach to achieve differential privacy. PABI’s strength lies in its ability to inject noise iteratively during the diffusion process, rather than just perturbing the final output. This approach is particularly crucial for graph data due to its interconnected nature, as traditional output perturbation methods often struggle to balance privacy and utility. The core idea is to leverage the contractive nature of many graph diffusion processes, where each iteration shrinks the distance between similar vectors. By carefully injecting noise at each step, PABI amplifies the privacy guarantees provided by each iteration, leading to stronger overall privacy. The paper likely explores different noise mechanisms (e.g., Laplace, Gaussian) and analyzes the theoretical privacy guarantees using techniques like Rényi Differential Privacy. A key challenge addressed is managing the sensitivity of graph diffusion, particularly for low-degree nodes. Strategies such as degree-based thresholding functions are probably introduced to mitigate this high sensitivity and improve utility. The overall impact is a framework offering stronger privacy guarantees for graph diffusion compared to traditional methods, while maintaining reasonable utility for downstream applications such as Personalized PageRank.

Noise Injection Methods

#

Differential privacy often employs noise injection to protect sensitive data. The choice of noise mechanism is crucial, impacting both the privacy guarantees and the utility of the results. Common approaches include adding Laplace or Gaussian noise, each with different properties. Laplace noise is often preferred for its suitability in L1 settings, while Gaussian noise is more widely used in L2 settings, sometimes offering a better utility-privacy trade-off. The paper likely explores these methods, potentially comparing their performance with various parameters such as the noise scale. Beyond the type of noise, the strategy of injection is also vital. Injecting noise at each iteration (iterative noise injection) can lead to stronger privacy amplification compared to a single round of noise addition at the output. The paper likely investigates these approaches, analyzing their privacy guarantees and the impact on the accuracy of the resulting graph diffusion algorithm. A careful analysis of the sensitivity of the computation is essential for appropriate noise scaling to achieve the desired privacy level. This might involve analyzing the impact of low-degree nodes and developing mechanisms to mitigate their effect on the privacy loss.

PPR Ranking Utility

#

Analyzing PPR (Personalized PageRank) ranking utility involves evaluating how effectively the algorithm incorporates personalization and privacy, while maintaining accurate ranking results. Effective personalization ensures the ranking reflects individual user preferences or node-specific characteristics, which is crucial for applications needing targeted results. Privacy mechanisms, such as differential privacy, are implemented to protect sensitive information within the graph data, balancing utility with privacy guarantees. Utility assessment focuses on comparing the PPR rankings against ground truth or a privacy-preserving baseline, using metrics like NDCG (Normalized Discounted Cumulative Gain) and Recall. A strong PPR ranking system demonstrates high utility by achieving high ranking accuracy under stringent privacy constraints. Computational efficiency also plays a vital role, as algorithms need to be scalable for large graphs. The overall goal is to find an optimal balance between personalization, privacy, accuracy, and efficiency in the PPR ranking process.

Future Graph Privacy

#

Future research in graph privacy needs to address several key challenges. Developing more efficient differentially private mechanisms is crucial, especially for large-scale graphs where computational costs are high. Current methods often struggle to balance privacy and utility, leading to inaccurate or unusable results. Exploring alternative privacy definitions beyond differential privacy is also necessary, as DP may be overly restrictive in certain graph applications. Advanced techniques like composition theorems or privacy amplification by iteration require further refinement for complex graph operations. Furthermore, the field needs robust methods for handling evolving graphs that adapt to dynamic changes in structure and data. Finally, research should focus on practical applications and real-world scenarios to ensure that privacy-preserving methods are implemented effectively.

More visual insights

#

More on figures

The figure compares the Rényi Differential Privacy (RDP) guarantees of the proposed method (Theorem 1) and the standard composition theorem for different numbers of iterations (K) in a graph diffusion process. The x-axis represents the number of iterations, and the y-axis shows the RDP privacy budget (ε). The plot demonstrates that the RDP budget for the proposed method remains relatively constant as the number of iterations increases, while the RDP budget for the composition theorem grows linearly. This highlights the advantage of the proposed method in maintaining strong privacy guarantees even with many iterations.

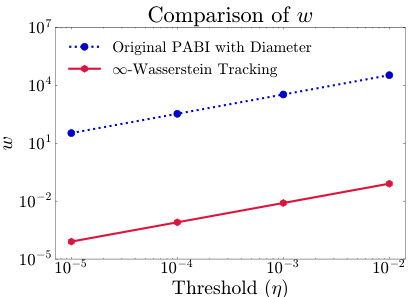
This figure compares the ∞-Wasserstein distance (a novel method introduced in the paper) to the diameter of the thresholding function (the original method from Altschuler et al. [27]). The results show that the ∞-Wasserstein distance provides a significantly tighter bound on the parameter set diameter, leading to a more practical and applicable privacy guarantee. The x-axis represents the threshold parameter (η), while the y-axis represents the distance metric (w). The plot demonstrates that the ∞-Wasserstein tracking method offers a substantially improved bound compared to using the diameter of the parameter set, especially as the threshold parameter increases.

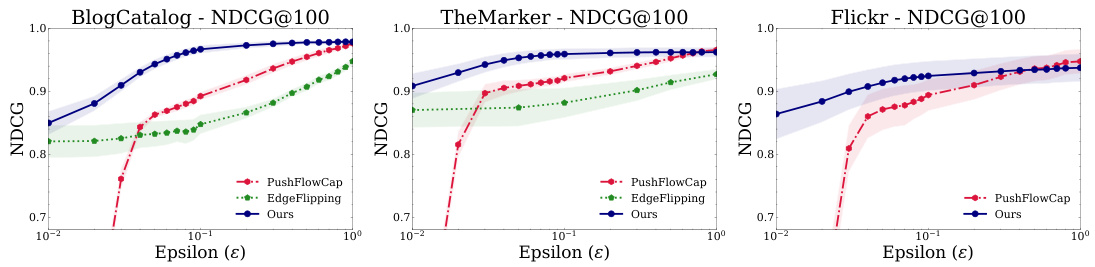
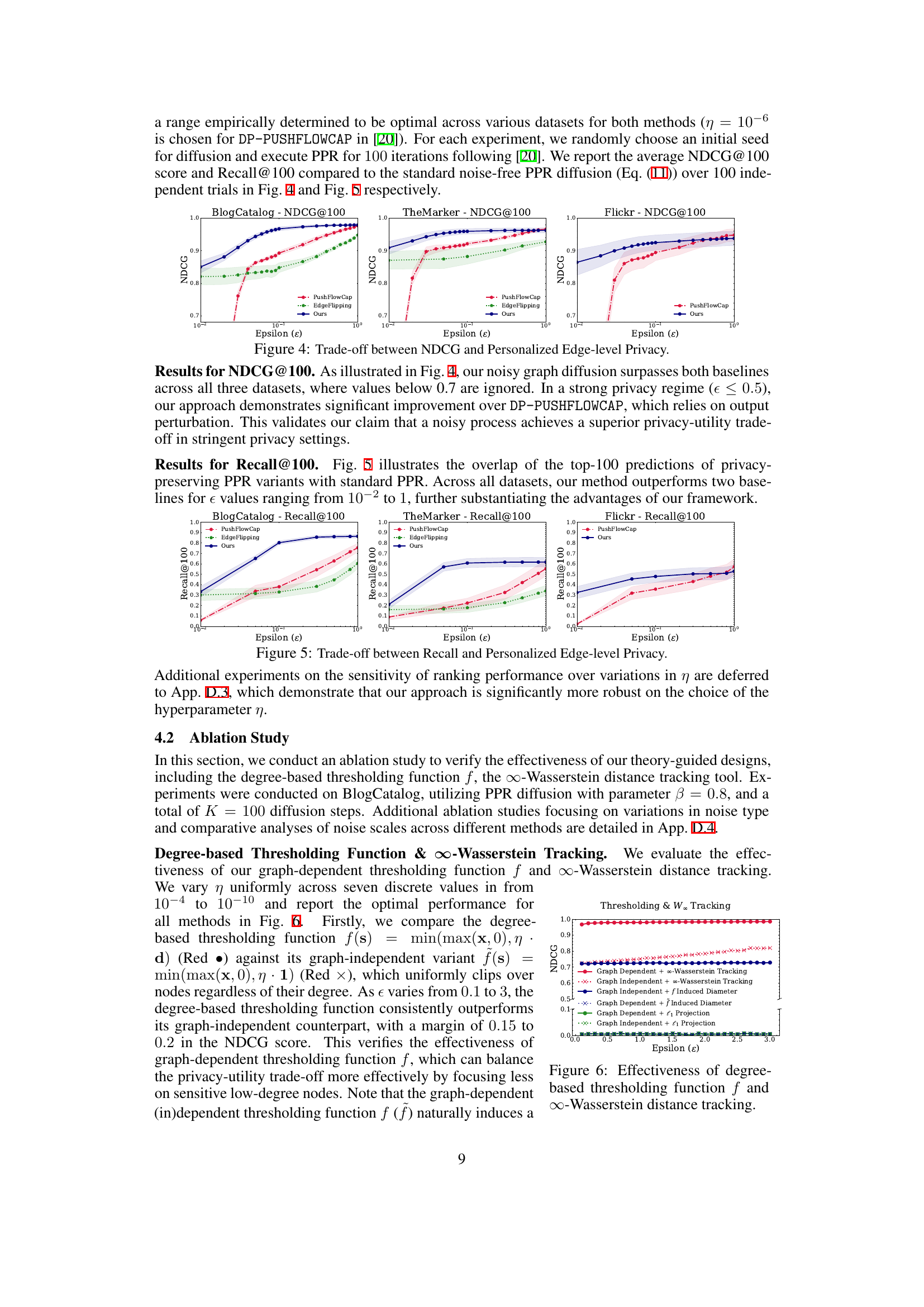
The figure compares the performance of three different approaches (PushFlowCap, EdgeFlipping, and the proposed method) for personalized PageRank computation under various privacy levels (epsilon). NDCG@100 is used as a metric to evaluate the ranking performance of the methods. The results are shown for three different datasets (BlogCatalog, TheMarker, and Flickr). The figure illustrates the trade-off between privacy (epsilon) and utility (NDCG@100) for each method across different datasets.

This figure compares the performance of three different methods (PushFlowCap, EdgeFlipping, and Ours) for personalized PPR computation on three real-world datasets (BlogCatalog, TheMarker, and Flickr) across various privacy budgets (epsilon). The Recall@100 metric is used to evaluate the ranking accuracy. Error bars are included. The figure shows that the ‘Ours’ method consistently outperforms the baselines, particularly in stricter privacy settings.

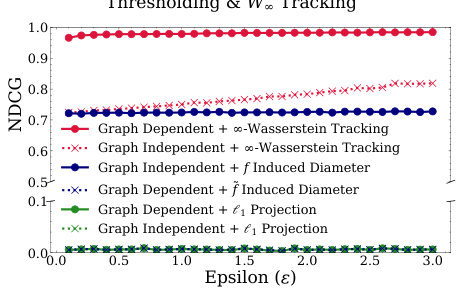
This figure shows the impact of using a degree-based thresholding function (f) and ∞-Wasserstein distance tracking on the privacy-utility tradeoff in the context of graph diffusion. The x-axis represents the privacy budget (epsilon, ε), and the y-axis represents the NDCG@100 score, a measure of ranking performance. Several methods are compared: Graph Dependent with ∞-Wasserstein tracking (best performance), Graph Independent with ∞-Wasserstein tracking (performs worse than graph-dependent method), Graph Dependent using the diameter induced by f (performs similarly to the graph-independent method with ∞-Wasserstein tracking), Graph Independent using the diameter induced by f, Graph Dependent with l1 projection (performs poorly), and Graph Independent with l1 projection (performs poorly). The results demonstrate the superiority of using both the degree-based thresholding and ∞-Wasserstein tracking for achieving a better balance between privacy and utility.

This figure demonstrates how edge perturbations in graphs with different node degrees lead to varying levels of distortion after graph diffusion. The left side illustrates an edge perturbation on a low-degree node, resulting in a relatively high distortion of 0.7 after diffusion. In contrast, the right side shows an edge perturbation on a high-degree node, producing a much lower distortion of 0.525. This highlights that edge perturbations on low-degree nodes have a greater impact on the graph diffusion process.

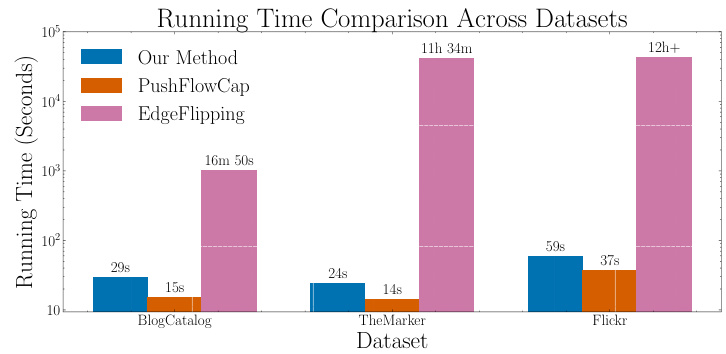
This figure compares the running time of three different methods (Our Method, DP-PUSHFLOWCAP, and Edge-Flipping) for computing Personalized PageRank (PPR) on three real-world datasets (BlogCatalog, TheMarker, and Flickr). The privacy budget is set to ε = 0.1. The results show that Our Method and DP-PUSHFLOWCAP are significantly faster than Edge-Flipping, especially as the dataset size increases. Edge-Flipping’s running time ranges from 16 minutes to over 12 hours. In contrast, Our Method and DP-PUSHFLOWCAP complete within 1 minute.

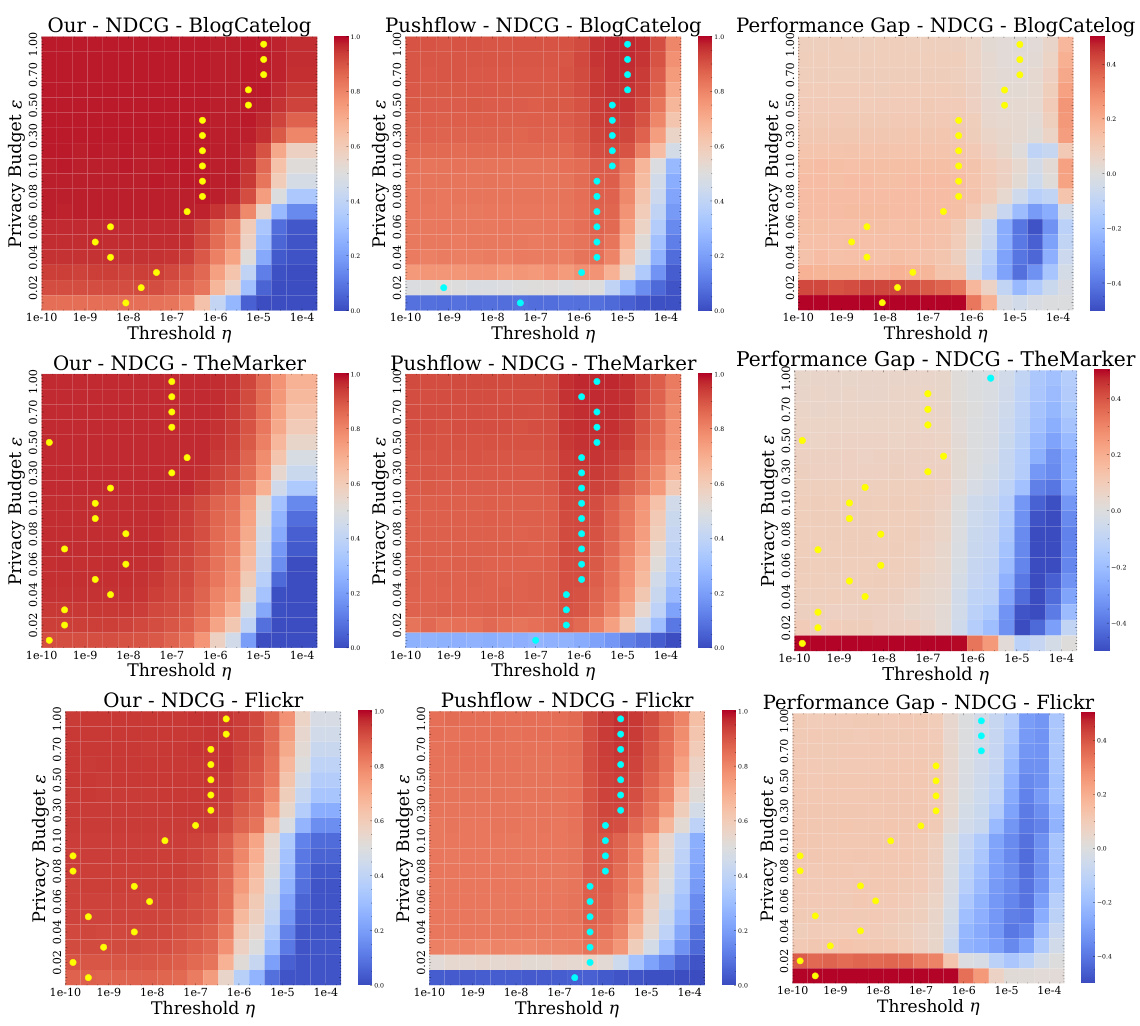
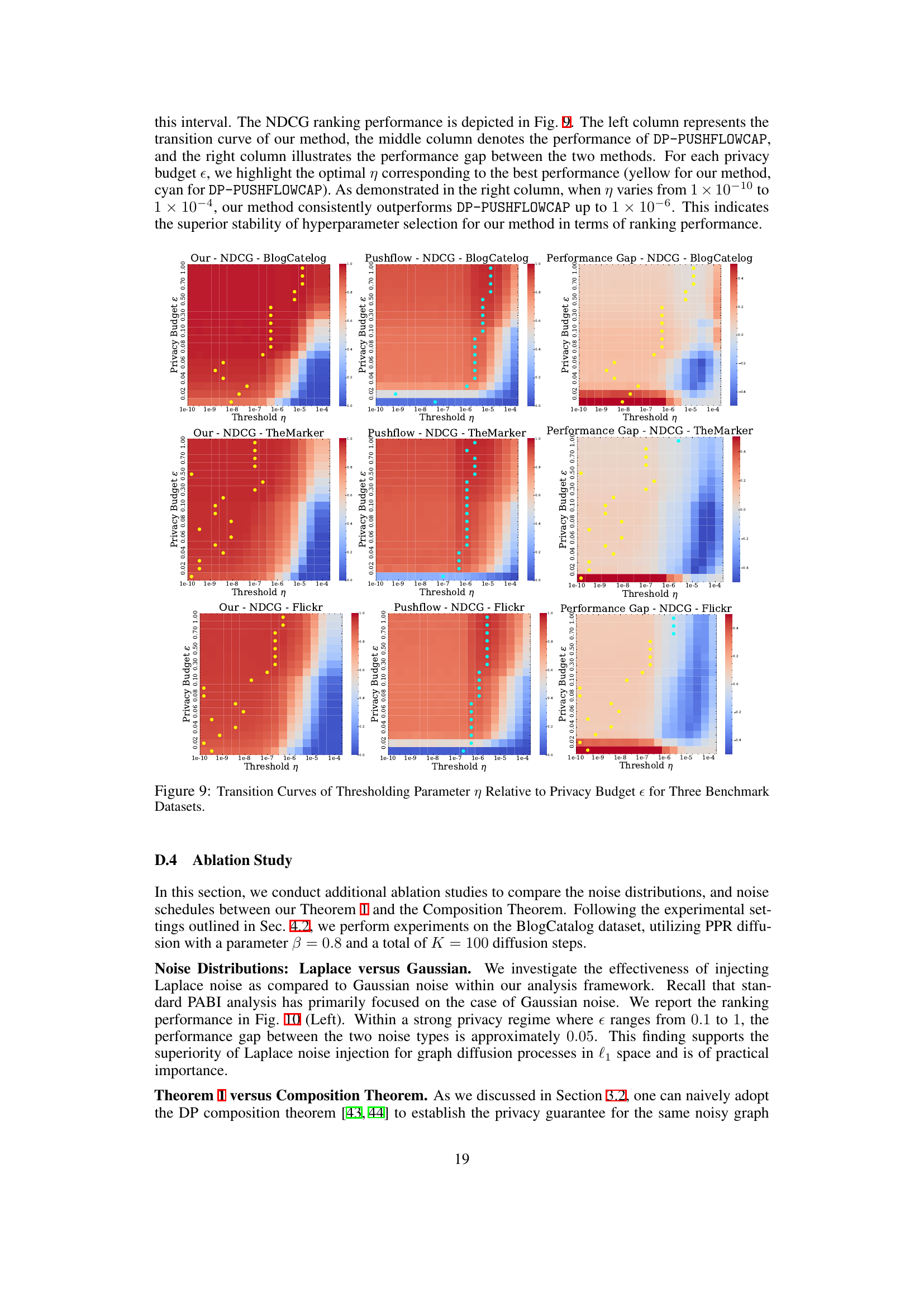
This figure displays heatmaps showing the relationship between the threshold parameter η, privacy budget ε, and NDCG@100 for three different datasets (BlogCatalog, TheMarker, Flickr). Each heatmap shows how the NDCG@100 score varies across different values of η and ε. The yellow dots highlight the optimal η value for each privacy budget. This visualization helps to understand the tradeoff between privacy and utility (NDCG score) and illustrates the impact of different thresholding strategies on the performance of the proposed differentially private personalized PageRank algorithm.

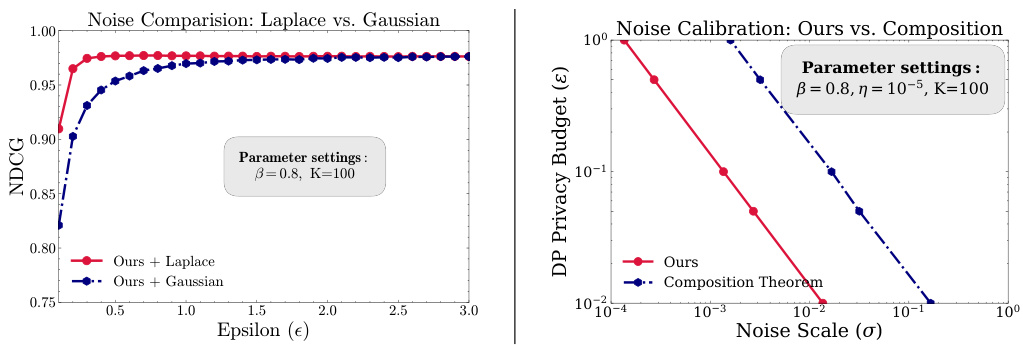
This figure compares the performance of using Laplace noise versus Gaussian noise in the proposed graph diffusion method. The left panel shows that Laplace noise consistently outperforms Gaussian noise across different privacy budgets (epsilon). The right panel illustrates a comparison of the required noise scales for achieving a target privacy budget epsilon, contrasting the proposed method’s noise calibration with the simpler composition theorem approach. The proposed method significantly reduces the noise scale needed to achieve the same privacy level.

Full paper

#