↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Estimating the density of a distribution from samples is a fundamental problem in statistics, often measured using the Wasserstein distance, especially when the geometry of the space is significant (e.g., estimating population densities). However, most existing algorithms focus on worst-case analysis, which can be overly pessimistic in practice. Existing algorithms don’t adapt to easy instances, resulting in suboptimal performance and higher error rates.
This paper addresses this limitation by designing and analyzing instance-optimal differentially private algorithms for density estimation in the Wasserstein distance. The algorithms adapt to easy instances, uniformly achieving instance-optimal estimation rates, and perform competitively with algorithms that have additional prior information about the data distribution. The work demonstrates uniformly achievable instance-optimal estimation rates in 1-dimension and 2-dimensions and extends to arbitrary metric spaces by leveraging hierarchically separated trees. This offers a major advancement towards efficient and accurate differentially private learning.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in differential privacy and machine learning. It introduces novel instance-optimal algorithms for density estimation, a fundamental problem with broad applications. By moving beyond worst-case analysis, the research opens new avenues for developing more efficient and accurate private learning algorithms, particularly relevant in data-sensitive fields. The results are also significant for understanding the fundamental limits of private density estimation, which has implications for diverse statistical applications.
Visual Insights#
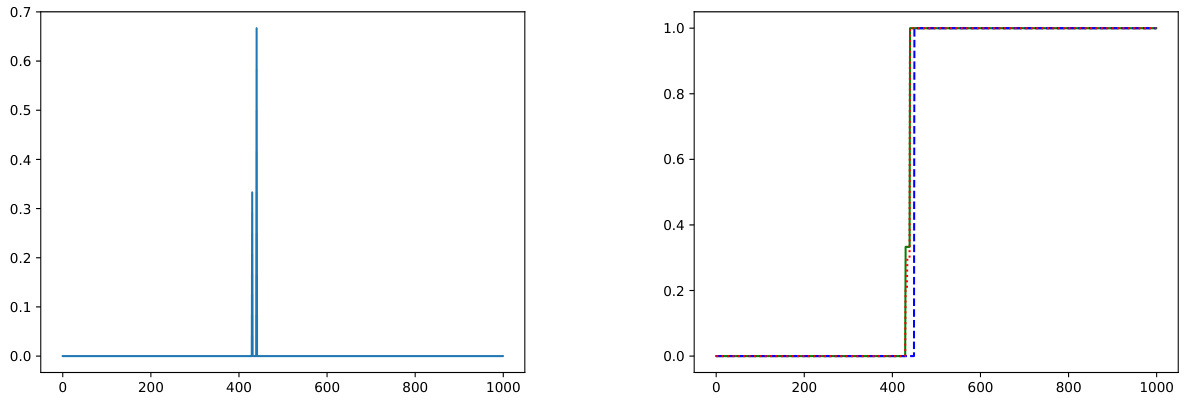
The figure shows a comparison of the performance of minimax optimal and instance-optimal algorithms on a sparsely supported distribution. The left panel shows the probability density function (pdf) of the distribution, while the right panel shows the cumulative distribution function (CDF) along with the CDFs learned by a minimax optimal algorithm and a differentially private instance-optimal algorithm. The instance-optimal algorithm outperforms the minimax optimal algorithm in terms of the Wasserstein distance (W1 error).
Full paper#