↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Reinforcement learning (RL) typically focuses on learning a single reward signal, limiting its applicability to complex scenarios with multiple objectives. Existing methods for learning multiple rewards often lack theoretical guarantees or are computationally expensive. This paper tackles these limitations by developing algorithms for multivariate distributional RL. A major challenge is the difficulty of modeling the full joint distribution of multiple rewards, which previous methods often failed to address fully or efficiently.
The researchers introduce novel, computationally tractable algorithms for both dynamic programming and temporal difference learning in multivariate distributional RL. These algorithms come with theoretical guarantees of convergence, matching the convergence rates observed in the simpler case of a single reward. Furthermore, the researchers also provide new insights into how the quality of approximate return distribution representations relates to the number of reward dimensions. The paper also introduces new techniques, including a randomized dynamic programming operator and a TD-learning algorithm, designed to improve efficiency and convergence in the high-dimensional case. Through simulations, they also show how different distribution representation choices influence the practical performance of multivariate distributional RL.
Key Takeaways#
Why does it matter?#
This paper is crucial because it presents the first computationally tractable and provably convergent algorithms for multivariate distributional reinforcement learning (RL). This addresses a major limitation of existing methods and opens new avenues for multi-objective decision-making, transfer learning, and representation learning in RL. The theoretical guarantees and novel algorithmic techniques are significant advancements that will benefit many RL researchers.
Visual Insights#
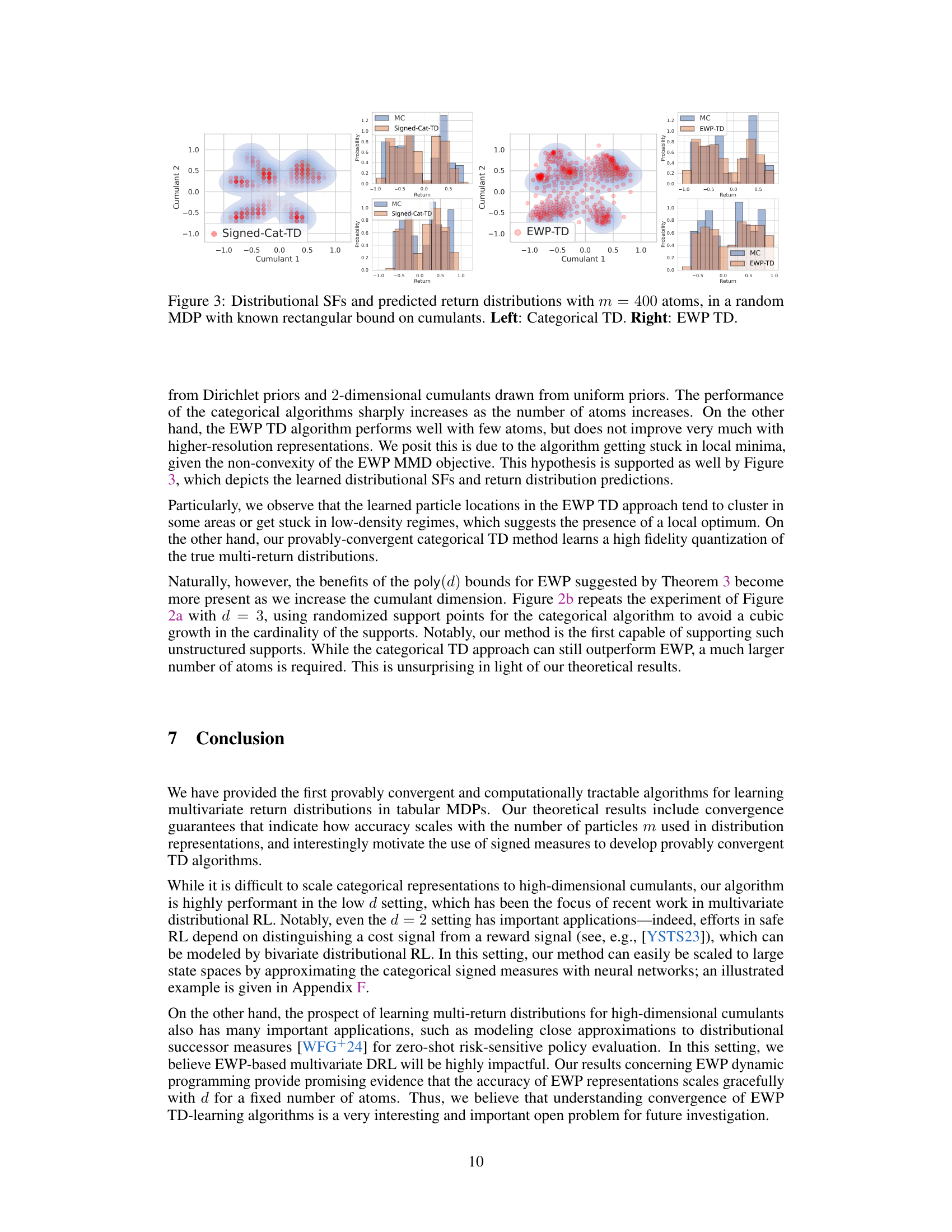
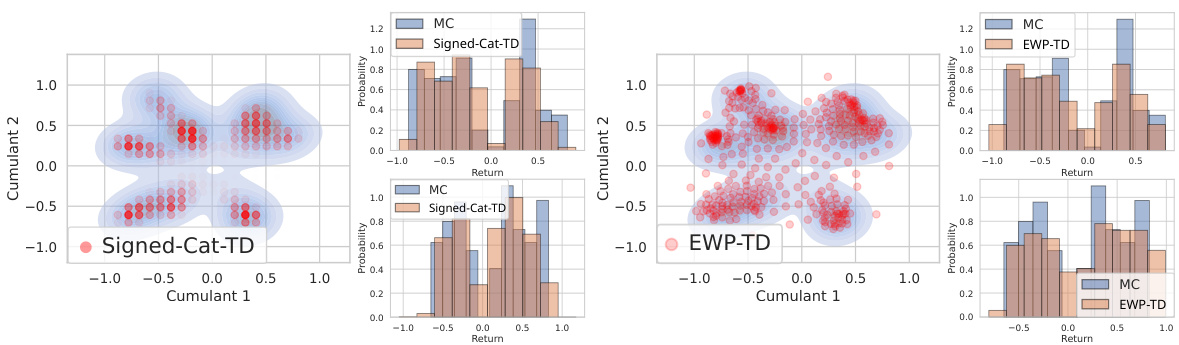
This figure compares the performance of categorical and EWP methods in approximating return distributions. The left side shows the results using categorical representation, while the right side displays the results with EWP representation. Both sides include simplex plots illustrating the distributional successor measure (DSM) and histograms representing predicted return distributions for two separate reward functions. This comparison helps to analyze the accuracy and efficiency of each method.

This table provides a concrete example showing that the categorical MMD projection operator (ΠC,κ) is not affine. It considers a single-state Markov Decision Process (MDP) with a 2-dimensional reward space R = {0, …, 3}2 and uses the energy distance kernel (induced by p(x, y) = ||x − y||2). Two probability distributions, p1 and p2, are defined, and their linear combinations (λp1 + (1 − λ)p2, with λ = 0.8) are compared. The table shows that the categorical projection of the linear combination is not equal to the linear combination of categorical projections (i.e., ΠC,κ(λp1 + (1 − λ)p2) ≠ λΠC,κ(p1) + (1 − λ)ΠC,κ(p2)), demonstrating the non-affine nature of the operator. The bolded entries highlight the discrepancies in the resulting probability distributions.
In-depth insights#
Multivariate DRL#
The concept of “Multivariate DRL” extends distributional reinforcement learning (DRL) to scenarios involving multiple reward signals. This significantly expands the applicability of DRL beyond single-objective tasks, enabling advancements in multi-objective decision-making and transfer learning. A key challenge lies in the increased computational complexity of handling multivariate return distributions. Existing methods often struggle with theoretical guarantees or rely on computationally expensive oracles. This research focuses on developing efficient and provably convergent algorithms for both dynamic programming and temporal difference learning in multivariate DRL. The algorithms address specific challenges unique to multivariate settings, such as the limitations of standard categorical TD learning. The study also investigates various distribution representation trade-offs and proposes novel projection techniques to improve efficiency and convergence.
EWP limitations#
Equally Weighted Particle (EWP) methods, while empirically successful in multivariate distributional reinforcement learning, suffer from significant limitations. Convergence guarantees are lacking, hindering reliable performance. The non-convexity of the MMD objective function with respect to particle locations leads to sensitivity to initialization and potential convergence to poor local optima. Furthermore, the computational cost increases exponentially with the number of particles and the dimensionality of the reward space, making it impractical for high-dimensional problems. Finally, standard theoretical analysis, typically relying on contraction properties, fails in the multivariate case, necessitating novel techniques to address the challenges posed by higher dimensional spaces. Therefore, improved algorithms or alternative representation methods are needed to fully address the limitations of EWP approaches.
Categorical TD#
Categorical TD learning, a core contribution of this research paper, presents a novel approach to multivariate distributional reinforcement learning. It addresses the computational challenges associated with directly applying the Bellman update to high-dimensional probability distributions by employing a categorical representation of return distributions. This method elegantly handles the complexity of approximating multi-dimensional distributions by leveraging a finite, and possibly state-dependent, support for the return distribution at each state. The use of a projection operator ensures the algorithm’s updates remain within the categorical representation, leading to theoretical guarantees of convergence. Importantly, to achieve convergence with the TD update, the categorical representation is extended to include signed measures, ensuring the projection operator’s linearity and allowing for a more tractable convergence analysis. The resulting algorithm is computationally efficient and theoretically sound, unlike previous methods that either lacked theoretical guarantees or required computationally expensive oracles. This method also allows for improved error bounds and thus offers a strong, robust approach for multivariate distributional reinforcement learning compared to prior particle-based methods, which were shown empirically to have issues with convergence.
Convergence rates#
The analysis of convergence rates in this research paper is crucial for understanding the efficiency and reliability of the proposed algorithms. The authors demonstrate that their algorithms achieve convergence rates comparable to those of existing methods in scalar reward settings, which is a significant achievement. This comparison provides a benchmark for evaluating the practical performance of multivariate distributional reinforcement learning. However, a deeper dive into these rates reveals nuances. The relationship between convergence speed and the dimensionality of the reward space is a key finding, highlighting computational challenges in high-dimensional environments. Furthermore, the impact of different distribution representations on the convergence rate is explored, demonstrating that the choice of representation can significantly affect algorithm performance. This aspect emphasizes the importance of selecting appropriate representations for specific applications.
Future work#
The paper’s ‘Future Work’ section could explore several promising avenues. Extending the theoretical analysis to non-tabular settings is crucial for real-world applications, requiring investigation into function approximation techniques and their impact on convergence. Developing more efficient algorithms for high-dimensional reward spaces is also key, potentially involving advanced dimensionality reduction methods or novel approximation strategies. Addressing the computational challenges associated with the proposed randomized dynamic programming and TD-learning approaches, especially in scaling to very large state spaces, is vital. Furthermore, empirical evaluation on a wider variety of tasks, including continuous control problems and multi-agent scenarios, would greatly enhance the paper’s impact and demonstrate the broad applicability of the proposed methods. Finally, a thorough investigation into the trade-offs between different distributional representations, considering factors like computational cost, representational power, and robustness to approximation errors, would provide valuable insights for practical implementation.
More visual insights#
More on figures
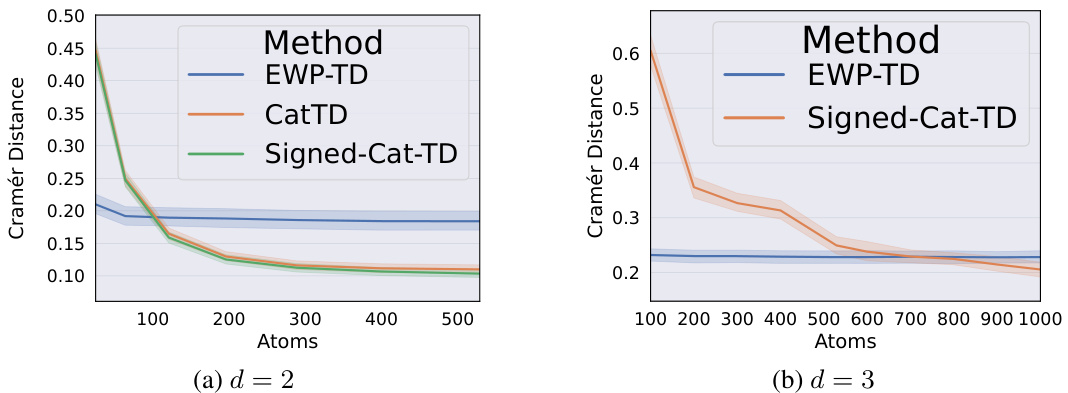
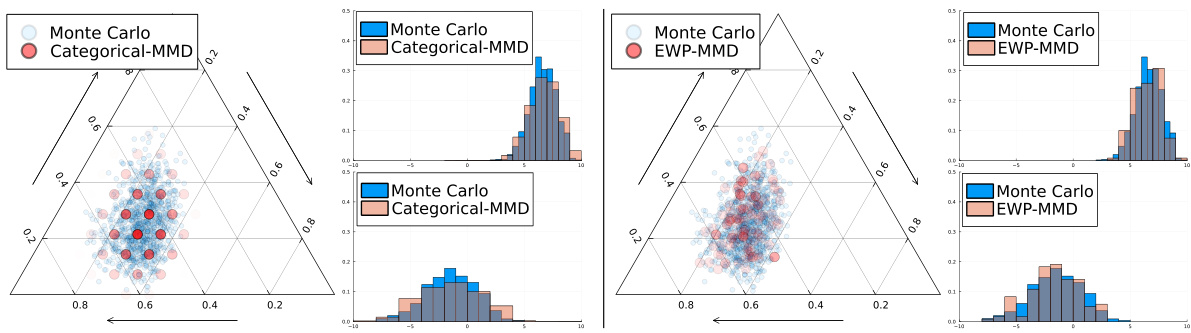
The figure shows the zero-shot return distribution prediction errors for two different dimensionality of cumulants (d=2 and d=3) using three different methods: EWP-TD, Categorical TD, and Signed-Cat-TD. The x-axis represents the number of atoms used in the return distribution representation. The y-axis represents the Cramér distance, which is a measure of the difference between the predicted return distribution and the true distribution. The shaded area around each line represents the 95% confidence interval. This figure demonstrates the accuracy and efficiency of the proposed methods in approximating the true return distribution.
This figure compares the performance of two different methods, categorical and EWP, for approximating multivariate return distributions in a 3-state Markov Decision Process (MDP). The left panels show the results using a categorical representation of the distributional successor measure (DSM), while the right panels use an equally-weighted particle (EWP) representation. Simplex plots visualize the learned DSM distributions, while histograms show the predicted scalar return distributions for two different reward functions not seen during training. This demonstrates the ability of the learned DSM to generate return distributions for unseen reward functions.
This figure visualizes the distributional successor measures (SMs) and predicted return distributions for both categorical and EWP representations. Simplex plots represent the learned SMs. Histograms show return distributions predicted using two held-out reward functions. This comparison highlights the differences in the quality of approximation between the two methods for representing return distributions.
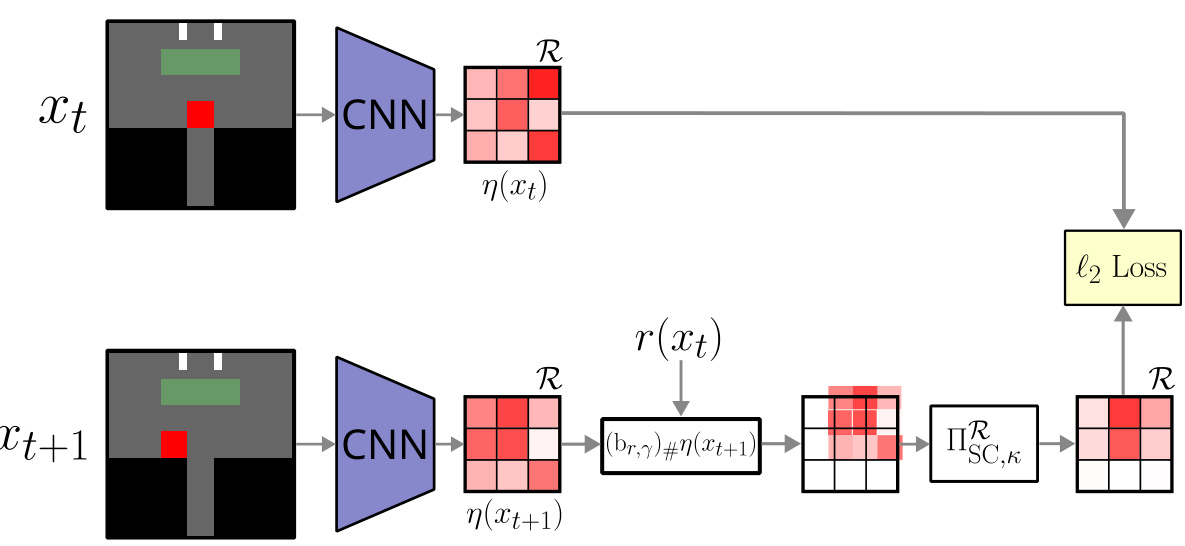
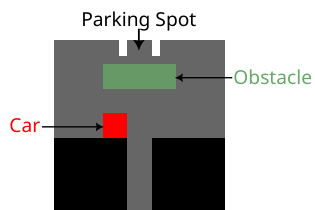
This figure shows the neural network architecture used for learning multivariate return distributions from image inputs in a continuous state space. It depicts how convolutional neural networks (CNNs) process the image observations (xt and xt+1) to generate return distribution representations (η(xt) and η(xt+1)). The architecture incorporates the multivariate distributional Bellman operator and a projection onto the space of signed measures. The final step involves computing an ℓ2 loss to train the model.
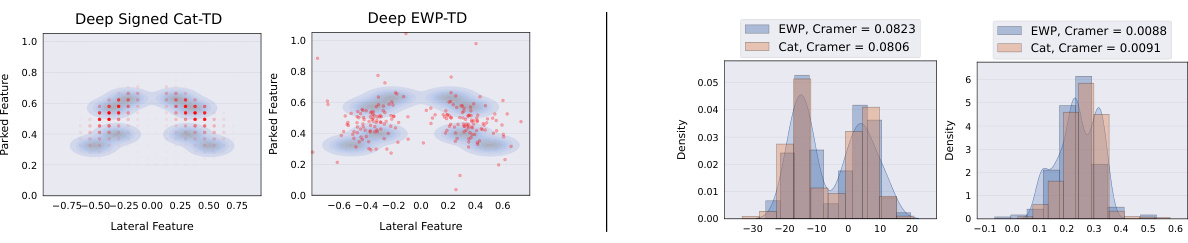
This figure compares the performance of categorical and EWP representations in approximating return distributions. The left side shows results from the categorical representation, while the right side shows those from the EWP (Equally Weighted Particles) representation. Simplex plots visualize the distributional successor measures (SMs), while histograms display the predicted return distributions generated using two distinct held-out reward functions. This allows a visual comparison of the accuracy and efficiency of both representation methods in approximating the return distribution.
Full paper#