On Feature Learning in Structured State Space Models

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with state-space models (SSMs), a rapidly growing area in deep learning. It addresses critical scaling challenges in SSMs, offering novel scaling rules that improve stability, generalization, and the transferability of hyperparameters. These findings are highly relevant to ongoing research trends and open new avenues for investigation in SSM design and training.

Visual Insights

#

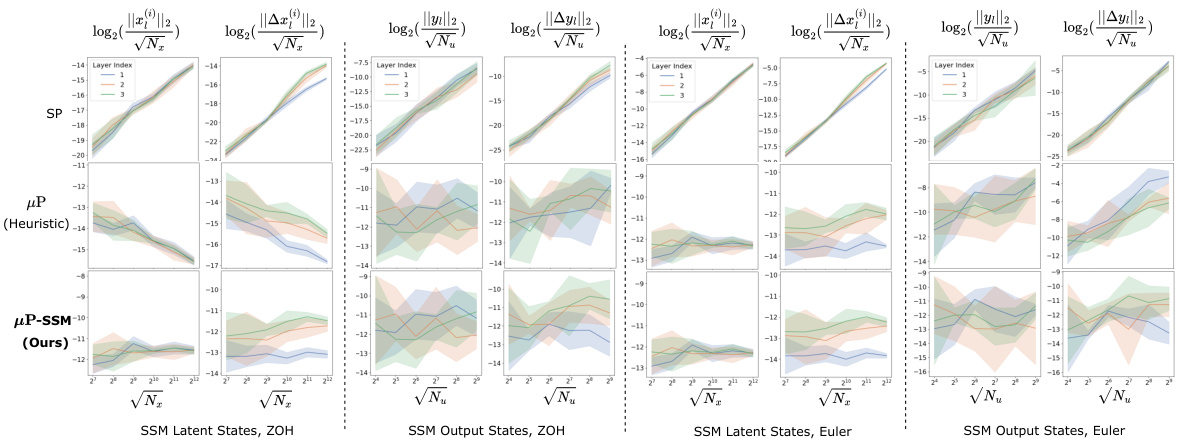
This figure compares the performance of three different scaling methods (µP-SSM, Standard Parameterization, and µP (heuristic)) on a Mamba model with three SSM layers. It shows the log2 of the L2 norm of the latent states (x) and output signals (y) for each layer, and the log2 of the L2 norm of their updates (Δx and Δy). The µP-SSM method demonstrates stable feature learning across all layers, while the other two methods experience either instability or vanishing updates, indicating failure to learn features effectively. The results are shown for both Zero-Order Hold (ZOH) and Euler discretization methods of the state transition matrix.

This table summarizes the scaling behavior of latent states, output signals, and their updates under different parameterizations (Standard Parameterization (SP), Maximal Update Parameterization (µP) (heuristic), and the proposed µP-SSM) for structured state-space models (SSMs). It compares the scaling behavior for two different discretization methods (Zero-Order Hold (ZOH) and Euler). The table shows how the norms of latent states (||x||2), output signals (||y1||2), and their updates (||∆x||2, ||∆y1||2) scale with respect to the network width (Nx and Nu) under each parameterization and discretization scheme. This highlights which parameterization leads to stable and non-trivial feature learning in SSMs.

In-depth insights

#

SSM Scaling Limits

#

The scaling behavior of state-space models (SSMs) is crucial for their effectiveness in handling long sequences. Understanding the SSM scaling limits is essential for optimizing model performance and stability. The paper investigates how SSMs learn features as network width approaches infinity, revealing that existing scaling rules, like Maximal Update Parameterization, fail to support feature learning because SSMs are not representable as Tensor Programs. The study highlights the inadequacy of relying on spectral scaling conditions commonly used in other architectures, as these do not transfer well to SSMs. Instead, a detailed signal propagation analysis leads to identifying an appropriate scaling rule for non-trivial feature evolution. This proposed scaling rule, while sharing similarities with Maximal Update Parameterization, ensures balanced forward and backward signal propagation, promoting stability, better generalization, and improved hyper-parameter transferability. These findings highlight the need for SSM-specific scaling strategies, demonstrating that a direct application of scaling techniques from other deep learning models may not be effective.

µP-SSM Approach

#

The µP-SSM approach presents a novel scaling method for structured state-space models (SSMs) like Mamba, addressing the limitations of existing scaling techniques like standard parameterization and the heuristic µP. It leverages a detailed signal propagation analysis to identify the appropriate scaling for both forward and backward passes in SSMs, ensuring stable and non-trivial feature evolution, even in the infinite-width limit. This is crucial because previous methods failed to support feature learning in SSMs due to their non-representability as Tensor Programs. The proposed µP-SSM scaling shows improved stability, better generalization, and importantly, demonstrates transferability of optimal hyperparameters from small to large-scale SSMs, mirroring the benefits observed in MLPs and Transformers. The key contribution lies in its rigorous theoretical justification and empirical validation showing improved performance on language modeling tasks, highlighting the practical significance of this unique scaling approach for training larger, more effective SSMs.

Mamba Analysis

#

The Mamba analysis section likely delves into the scaling behavior of the Mamba model, a structured state-space model. It probably investigates how Mamba’s performance changes as its width (number of channels or units) and depth (number of layers) increase. The analysis likely involves signal propagation analysis, examining how signals flow forward and backward through the network, revealing the optimal scaling rules for parameters. Tensor Programs may be used to formally analyze the model’s infinite-width behavior and to rigorously derive the appropriate scaling. Crucially, the analysis likely compares Mamba’s scaling to established methods like maximal update parameterization, highlighting where it differs and how it could improve stability, generalization, and hyperparameter transferability. Empirical validation is also vital, demonstrating the model’s performance at different scales with and without applying the proposed scaling, using metrics like test loss or perplexity. The analysis ultimately aims to guide the effective scaling of Mamba for optimal performance in real-world applications.

Feature Learning

#

The concept of ‘feature learning’ within the context of scaling state-space models (SSMs) is crucial because it determines the models’ ability to extract meaningful representations from data as their size increases. The research highlights that traditional scaling methods, like maximal update parameterization, fail to facilitate feature learning in SSMs due to their non-representability as Tensor Programs. This emphasizes the necessity of a novel understanding of signal propagation—both forward and backward—within SSMs to uncover appropriate scaling rules for successful feature evolution in the infinite-width limit. The paper’s proposed solution, which exhibits improved stability, generalization and hyper-parameter transferability, suggests that a deeper analysis of the intrinsic dynamics of SSMs is necessary for optimizing feature learning, especially at scale. The findings underscore the limitations of applying established scaling techniques to all neural network architectures and advocate for a more architecture-specific approach to scaling for optimal performance.

Future of SSMs

#

The future of structured state-space models (SSMs) appears bright, driven by their ability to handle long sequences efficiently and learn complex features. Overcoming limitations in scaling and feature learning, as highlighted in the paper, is crucial for realizing their full potential. Developing theoretical frameworks beyond Tensor Programs to better analyze SSMs is essential. Addressing the non-representability of SSMs within the Tensor Program framework will enable the development of more sophisticated scaling rules, improving stability and generalization. The ability to transfer optimal hyperparameters across model sizes, a property similar to that of MLPs, needs further investigation. Research should focus on making SSMs more suitable for tasks like language modeling, where they currently lag behind transformers. Bridging the gap between theoretical understanding and practical implementation will be key. This might involve exploring novel discretization techniques, architectures, and training methods specific to SSMs. Finally, investigating the interaction between various components within SSMs is critical to unlocking their full capabilities and addressing challenges such as vanishing/exploding gradients.

More visual insights

#

More on figures

This figure illustrates the architecture of the Mamba S6 layer, a key component of the Mamba model. The computation is broken down into three stages: Selection, Discretization, and Per-Channel Linear Recurrence. The selection stage dynamically generates weight matrices based on the input. Discretization then applies either Zero-Order Hold (ZOH) or Euler methods. Finally, per-channel linear recurrences enable parallel processing for each input channel. The diagram clearly shows the flow of information and the location of trainable parameters (shown in blue).

This figure compares the performance of three different scaling methods (µP-SSM, Standard Parametrization, and µP (heuristic)) for training Structured State Space Models (SSM). The µP-SSM method, proposed by the authors, demonstrates stable feature learning across all three layers of the SSM. In contrast, the other two methods show instability or vanishing updates, indicating a failure to learn features effectively. The figure showcases results for both Zero-Order Hold (ZOH) and Euler discretization methods for the state transition matrix.

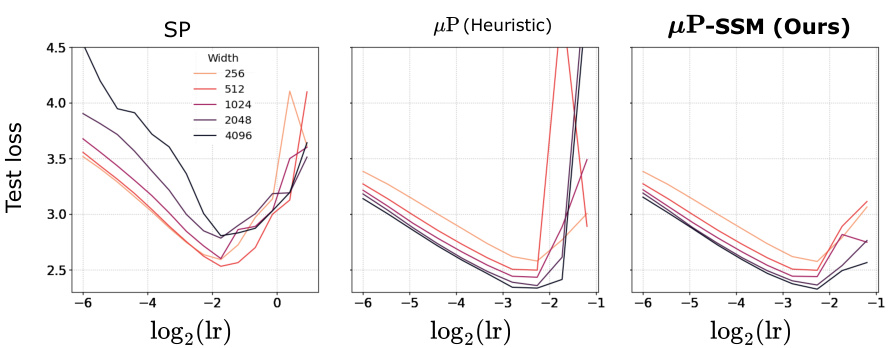
This figure compares the performance of three different scaling methods (µP-SSM, Standard Parameterization, and µP Heuristic) on a structured state space model called Mamba. The results demonstrate that µP-SSM is the only method which enables feature learning in the model across three different layers, while other methods lead to issues such as instability or vanishing updates. The figure also shows results obtained using two different numerical integration methods for the state update equation (Zero-Order Hold and Euler).

The figure compares the performance of three different scaling methods (Standard Parameterization, Heuristic µP, and proposed µP-SSM) for training Structured State Space Models (SSM). It shows that only the µP-SSM scaling allows for successful feature learning in all three layers of the model, as evidenced by stable and non-vanishing updates to latent states and output signals. The other two methods suffer from instability or vanishing updates, highlighting the importance of the proposed scaling method.

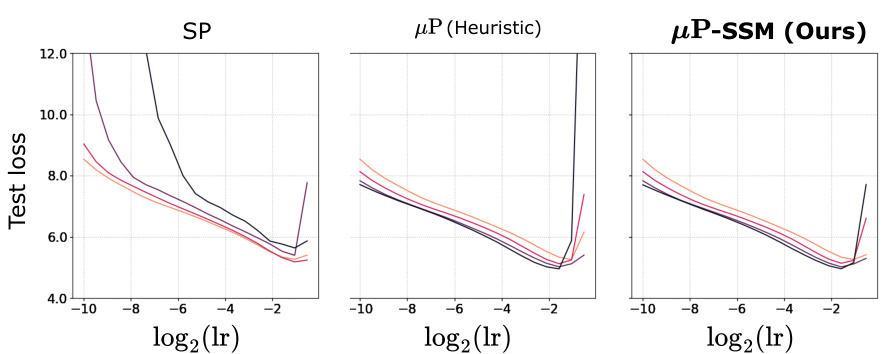
The figure displays the test loss of the Mamba model with different scaling methods (Standard Parametrization, µP (heuristic), and µP-SSM) against different learning rates and varying model widths. µP-SSM shows significantly better performance and stability, particularly at higher learning rates, compared to the other methods. It also demonstrates stable hyperparameter transfer across model sizes, unlike the other methods.

Full paper

#