↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Bandit convex optimization (BCO) deals with the challenge of learning optimal actions from limited feedback, made harder when feedback is delayed. Existing algorithms for delayed BCO had a significant gap between their regret bounds and the theoretical lower bound. This gap is problematic because the regret, representing the cumulative difference between an algorithm’s performance and the optimal strategy, is a key metric for evaluating the effectiveness of BCO algorithms.
This research introduces a novel algorithm, called D-FTBL (Delayed Follow-The-Bandit-Leader). It cleverly incorporates a blocking update mechanism which separates the effects of delays and noisy feedback measurements. The results show that D-FTBL achieves a significantly improved regret bound, effectively closing the gap with the theoretical lower bound. Furthermore, the algorithm shows adaptability in scenarios with strongly convex functions, making it useful in a wider range of practical applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in online convex optimization and bandit algorithms due to its significant improvement on regret bounds for problems with delayed feedback. It provides tight theoretical guarantees and practical algorithms, addressing a critical gap in existing research. The results also offer valuable insights and new avenues for research in related fields like online routing and online advertising, where delays are inherent challenges.
Visual Insights#
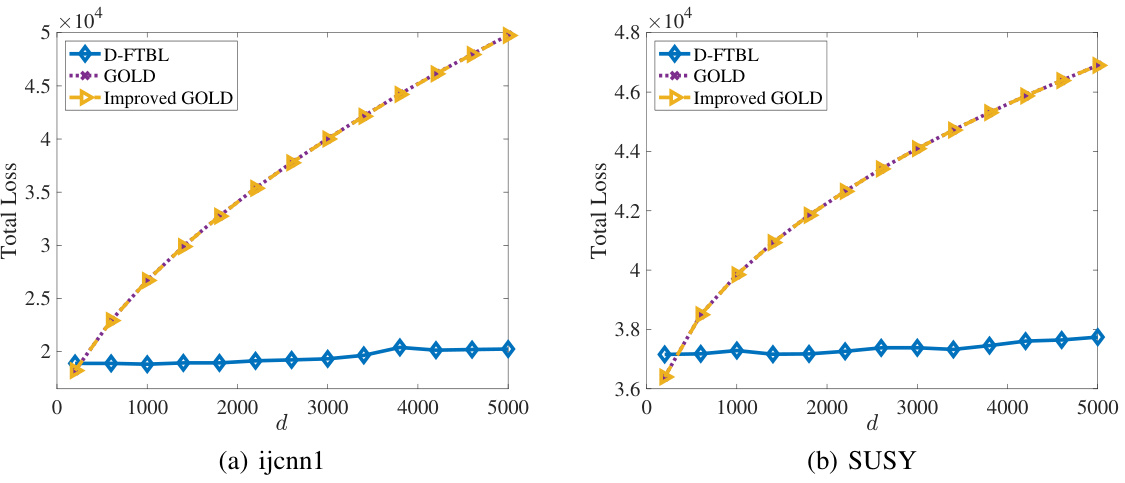
This figure shows the total loss of three algorithms (D-FTBL, GOLD, and Improved GOLD) on two datasets (ijcnn1 and SUSY) for different maximum delays (d). The x-axis represents the maximum delay, and the y-axis represents the total loss. The plot demonstrates the performance comparison of the algorithms in a delayed online binary classification setting. D-FTBL generally shows lower loss than the other two algorithms, especially as the maximum delay increases.
Full paper#