TL;DR#
Neural Ordinary Differential Equations (Neural ODEs) offer continuous-depth neural networks; however, applying traditional Batch Normalization (BN) has proven problematic. This is due to BN’s design for discrete networks, leading to variable step sizes and issues with time grids in Neural ODEs’ forward pass, hindering accurate statistics calculation for normalization. This also impacts performance, particularly with small batch sizes and outliers.
To overcome this, the researchers introduce Temporal Adaptive Batch Normalization (TA-BN), a novel technique that adapts to the continuous-time nature of Neural ODEs. TA-BN utilizes adaptive time grids and interpolation to estimate population statistics. Experiments on image classification and physical system modeling show that TA-BN significantly improves Neural ODE performance, enabling deeper models and surpassing existing approaches, particularly concerning parameter efficiency. It enables the stacking of more layers and achieves 91.1% accuracy on CIFAR-10.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with Neural ODEs. It identifies a critical limitation in applying traditional batch normalization and proposes a novel solution, TA-BN, that significantly improves training and performance. This has major implications for scaling Neural ODEs to tackle complex problems and opens new avenues for research in continuous-depth neural networks. The improved efficiency and ability to train deeper networks are of significant interest.
Visual Insights#
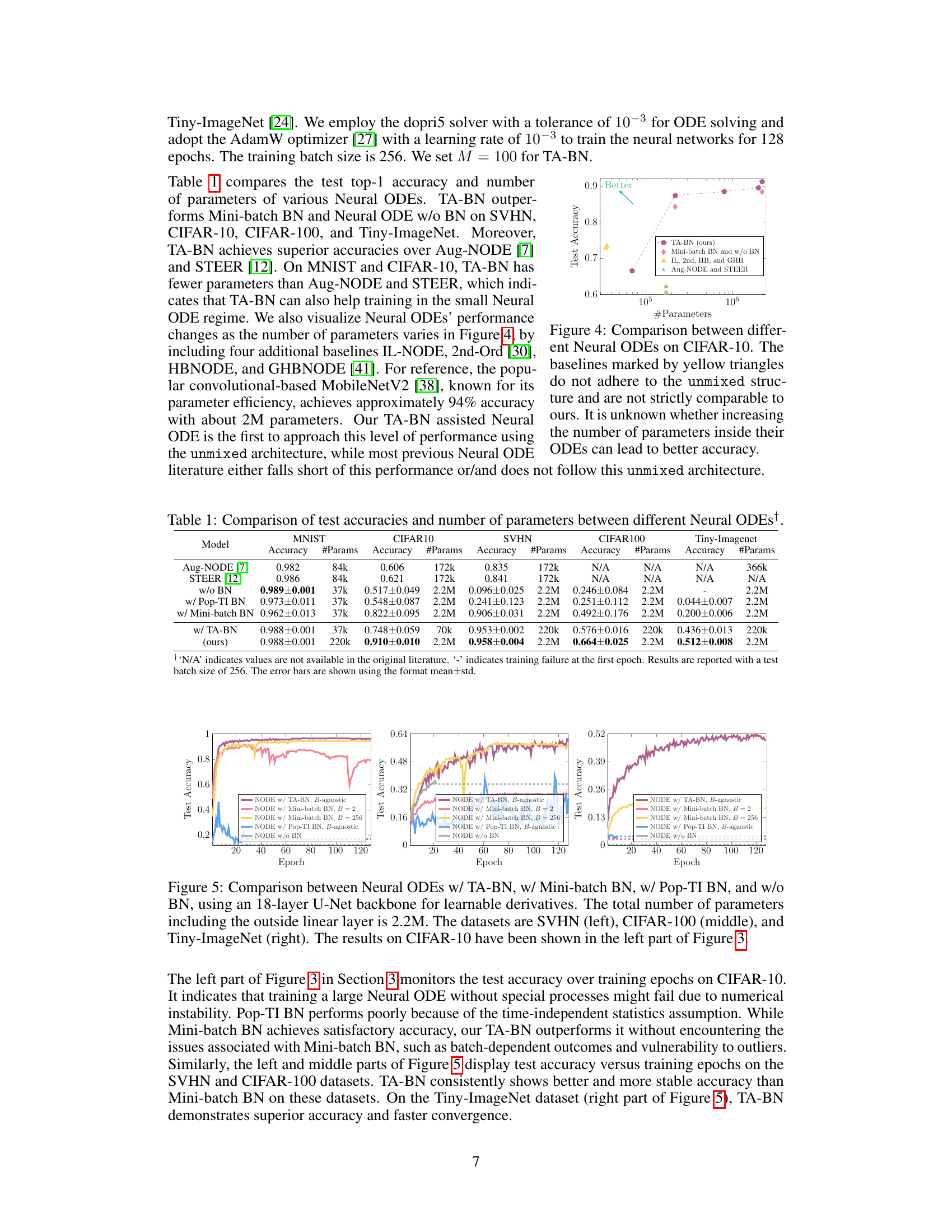
🔼 This figure shows the test accuracy curves of Neural ODEs with varying numbers of convolution layers (4, 8, 12, 18 layers) trained on the CIFAR-10 dataset. The curves illustrate the impact of increasing the depth of the Neural ODE on model performance. It demonstrates the instability of deeper Neural ODEs without batch normalization, as indicated by the dashed horizontal lines representing training failures. The figure also includes results for Neural ODEs with traditional mini-batch Batch Normalization (BN) and the proposed Temporal Adaptive Batch Normalization (TA-BN) to highlight the performance improvement.
read the caption
Figure 1: Test accuracies are depicted over the training epochs on CIFAR-10, utilizing Neural ODEs with different numbers of convolution layers as the backbones for learnable derivatives. Dashed horizontal lines denote instances of training failures.
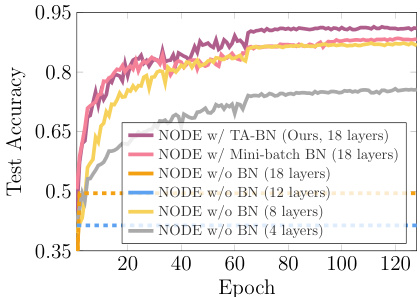
🔼 This table compares the performance of different Neural ODE models on various image classification datasets (MNIST, CIFAR-10, SVHN, CIFAR-100, and Tiny-ImageNet). The models include Aug-NODE, STEER, and variations using TA-BN (the proposed method), Pop-TI BN, mini-batch BN, and no BN. For each model and dataset, the table lists the test accuracy and the number of parameters. The † symbol likely indicates a footnote with additional details or explanations, possibly regarding the experimental setup or evaluation metrics.
read the caption
Table 1: Comparison of test accuracies and number of parameters between different Neural ODEs†.
In-depth insights#
TA-BN: A Deep Dive#
A deep dive into TA-BN (Temporal Adaptive Batch Normalization) reveals its ingenious solution to the limitations of traditional Batch Normalization (BN) within Neural Ordinary Differential Equations (Neural ODEs). TA-BN directly addresses the mismatch between BN’s discrete nature and the continuous-time dynamics of Neural ODEs. By employing adaptive step-size solvers, TA-BN calculates temporal derivatives at variable time intervals, unlike fixed-step methods. The adaptive approach is crucial because traditional BN relies on consistent time grids for computing mini-batch statistics, which is not guaranteed with adaptive solvers. TA-BN overcomes this by interpolating population statistics across these variable time points, ensuring consistent normalization across batches and maintaining accuracy even with small batch sizes. This adaptive interpolation is key to TA-BN’s success in enabling training of deeper Neural ODEs without encountering the instability issues that plague standard BN implementations. The effectiveness of this technique in scaling up Neural ODE model sizes, enhancing accuracy and efficiency is particularly noteworthy. TA-BN’s superior performance in image classification and physical system modeling showcases its broad applicability and presents a significant advancement in Neural ODE training.
Neural ODE Scaling#
Neural ODEs, while offering continuous-depth representation, face challenges in scaling. Traditional methods struggle to maintain performance when increasing the network’s depth or complexity. The core issue lies in the inherent mismatch between traditional batch normalization (BN), designed for discrete layers, and the continuous nature of Neural ODEs. This mismatch leads to unstable training and degraded accuracy as model size grows. The paper introduces Temporal Adaptive Batch Normalization (TA-BN) to address this limitation. TA-BN acts as a continuous-time analogue to BN, enabling stable training even with significantly deeper models. This addresses the performance saturation observed in previous Neural ODE architectures. Through extensive experiments, the researchers showcase TA-BN’s effectiveness in significantly improving accuracy and efficiency, even surpassing MobileNetV2 levels of parameter efficiency in some cases. The key is TA-BN’s ability to learn time-dependent statistics that resolve the instability problems caused by the variable step-sizes of adaptive ODE solvers. This allows for better generalization across various datasets and tasks.
Adaptive BN Limits#
The concept of ‘Adaptive BN Limits’ in the context of Neural ODEs suggests exploring the boundaries and potential drawbacks of adapting batch normalization (BN) for continuous-time systems. Traditional BN, designed for discrete networks, faces challenges when directly applied to Neural ODEs due to the variable time steps in the solver. Adaptive methods attempt to address this mismatch, but they may introduce limitations. For example, relying on mini-batch statistics for normalization can lead to inaccurate or unstable results, especially with small batch sizes or noisy data. Population statistics, while potentially more stable, might be unavailable or inaccurate during inference, as the discretization process varies between training and testing. Therefore, investigating the limits of adaptive BN involves carefully examining these trade-offs and exploring alternative normalization techniques better suited to the continuous nature of Neural ODEs, possibly techniques that explicitly model time-dependence. This exploration could reveal novel methods that surpass the performance of traditional BN while maintaining stability and efficiency.
Physical System Test#
In a hypothetical ‘Physical System Test’ section of a research paper, one would expect a rigorous evaluation of a proposed method’s performance on real-world physical systems. This would likely involve applying the method to various physical scenarios, comparing its results against established baselines or ground truth data. The section should detail the experimental setup, including the specific physical systems used, the data acquisition process, and any pre-processing steps. Crucially, it needs to define the metrics used for evaluating performance and present the results clearly and comprehensively, likely including statistical analysis to assess significance and robustness. A thoughtful discussion of the findings is critical, interpreting the results in the context of the physical system’s behavior and identifying any limitations or areas for improvement. The presence of visualizations such as plots or tables is important to enhance clarity and comprehension, supporting the claims made regarding accuracy and efficiency. Overall, a robust ‘Physical System Test’ section would showcase the practical applicability and effectiveness of a proposed method beyond theoretical or simulated settings, offering valuable insights into its real-world implications and limitations.
Future Work: ODEs#
Future research directions in Neural ODEs could explore several promising avenues. Improving the efficiency of the ODE solvers is crucial, especially for very deep networks, as the computational cost can become prohibitive. Investigating novel numerical methods specifically designed for the challenges presented by neural networks within the ODE framework would be highly impactful. Another important area is exploring alternative architectures, moving beyond the simple chaining of ODE layers with linear layers. This may involve integrating ODEs with other neural network components more effectively, or developing completely new continuous-time network architectures. Finally, a deeper theoretical understanding of Neural ODEs is needed. This includes developing more robust mathematical frameworks for analyzing their properties, particularly stability and generalization abilities, and for making more accurate comparisons between discrete and continuous neural networks. Addressing the challenges of handling missing data, irregular time series, and high-dimensional state spaces within the ODE framework is crucial for wider applicability. These advancements could make Neural ODEs a more powerful and versatile tool for machine learning.
More visual insights#
More on figures
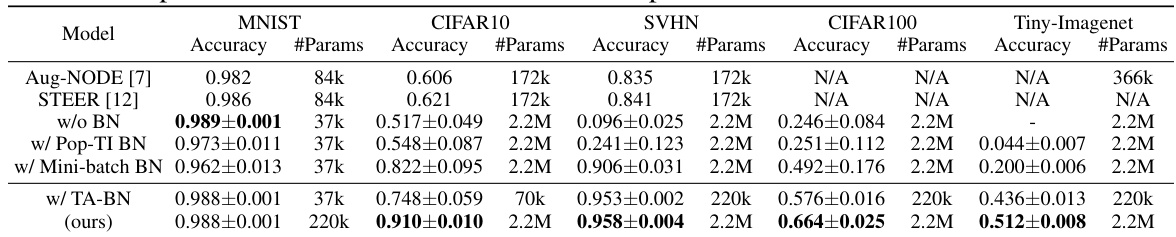
🔼 This figure illustrates the limitations of traditional batch normalization (BN) in Neural ODEs and introduces the proposed Temporal Adaptive Batch Normalization (TA-BN). The left panel shows how the variable time steps used by adaptive ODE solvers in the forward pass lead to misaligned time grids during training and testing, preventing the reliable accumulation of population statistics. This problem affects both Population Batch Normalization (Pop BN) and a time-independent version called Pop-TI BN. The right panel showcases how TA-BN addresses this issue by employing temporal interpolation to accumulate running statistics and update parameters consistently during both training and testing.
read the caption
Figure 2: Left: The failure of Pop BN in Neural ODEs stems from the misalignment of discretized time grids. Pop-TI BN aggregates all running mini-batch statistics into a single pair of (μ, σ²), implicitly assuming time-independent population statistics. Right: Our proposed TA-BN automatically conducts temporal interpolation to accumulate statistics and update parameters during training and testing.

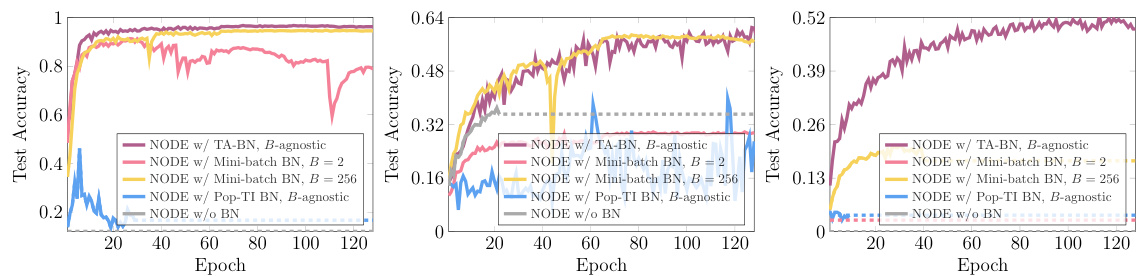
🔼 This figure compares the performance of three different batch normalization methods (TA-BN, mini-batch BN, and Pop-TI BN) for training Neural ODEs on the CIFAR-10 dataset. The left panel shows that TA-BN maintains high accuracy across different batch sizes, unlike mini-batch BN, which suffers from accuracy degradation with small batch sizes. Pop-TI BN shows erratic behavior due to its time-independent statistics assumption. The middle panel demonstrates TA-BN’s robustness to noisy data compared to mini-batch BN. The right panel visualizes the time-dependent nature of the output statistics generated by the Neural ODE.
read the caption
Figure 3: Left: We train a Neural ODE with a U-Net backbone as the learnable derivatives on CIFAR-10. Mini-batch BN shows degraded accuracies with a batch size of 2, while TA-BN can maintain high accuracies under varying batch sizes, because it uses the estimated population statistics during testing. Pop-TI BN aggregates running statistics encountered at any time points into a single pair of μ and σ². This approach assumes time-independent statistics, leading to erroneous predictions and erratic test loss curves. Middle: When noisy data exist on average in one out of every test batch, Mini-batch BN's performance deteriorates, because the noise affects the mini-batch statistics. The backbone for learnable derivatives in this experiment consists of 6 convolution layers. Right: We plot the output statistics from the first layer of U-Net over time; they are time-dependent.
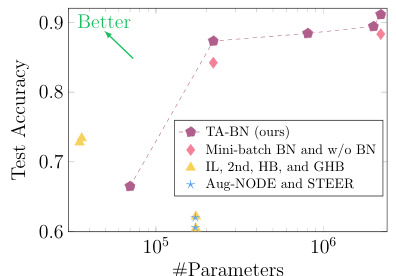
🔼 This figure compares the performance of different Neural ODE architectures on CIFAR-10, focusing on the relationship between the number of parameters and test accuracy. The primary method being compared against is the proposed TA-BN method, which shows improved performance with increased model size. Other Neural ODE methods are shown, some of which do not follow the same ‘unmixed’ architectural pattern as the TA-BN model, which makes direct comparison difficult. The figure highlights TA-BN’s ability to scale effectively without performance saturation, unlike other methods.
read the caption
Figure 4: Comparison between different Neural ODEs on CIFAR-10. The baselines marked by yellow triangles do not adhere to the unmixed structure and are not strictly comparable to ours. It is unknown whether increasing the number of parameters inside their ODEs can lead to better accuracy.
🔼 This figure compares the performance of different batch normalization methods (TA-BN, mini-batch BN, Pop-TI BN) for training Neural ODEs on the CIFAR-10 dataset. The left panel shows that TA-BN maintains high accuracy across various batch sizes, unlike mini-batch BN which suffers at small batch sizes. The middle panel demonstrates TA-BN’s robustness to noisy data, contrasting with mini-batch BN’s vulnerability. The right panel visually confirms the time-dependency of the statistics within the Neural ODE.
read the caption
Figure 3: Left: We train a Neural ODE with a U-Net backbone as the learnable derivatives on CIFAR-10. Mini-batch BN shows degraded accuracies with a batch size of 2, while TA-BN can maintain high accuracies under varying batch sizes, because it uses the estimated population statistics during testing. Pop-TI BN aggregates running statistics encountered at any time points into a single pair of μ and σ². This approach assumes time-independent statistics, leading to erroneous predictions and erratic test loss curves. Middle: When noisy data exist on average in one out of every test batch, Mini-batch BN's performance deteriorates, because the noise affects the mini-batch statistics. The backbone for learnable derivatives in this experiment consists of 6 convolution layers. Right: We plot the output statistics from the first layer of U-Net over time; they are time-dependent.
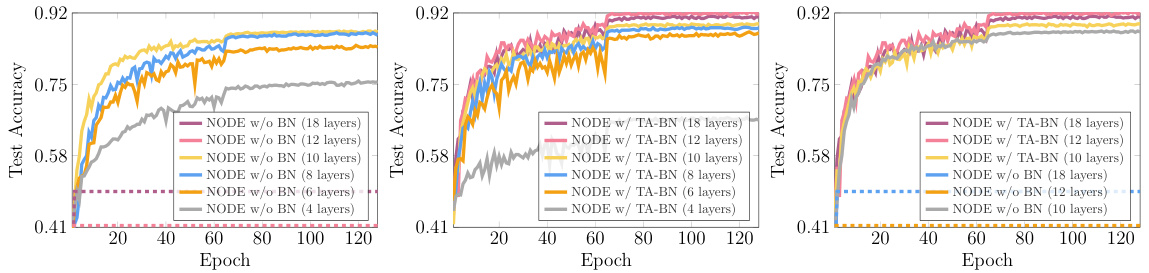
🔼 This figure compares the performance of Neural ODEs with and without TA-BN on CIFAR-10, demonstrating the scaling capabilities of TA-BN. The left panel shows that Neural ODEs without BN fail to train effectively when the number of layers increases beyond a certain point, while the middle panel demonstrates that TA-BN successfully allows for the training of deeper Neural ODEs. The right panel directly compares the performance of both settings.
read the caption
Figure 6: CIFAR-10 accuracies with increasing sizes of the backbones for learnable derivatives. These figures illustrate the scaling up of Neural ODEs without BN (left) and Neural ODEs with TA-BN (middle). We also compare the accuracies of these two settings in one figure (right).

🔼 This figure compares the performance of different batch normalization methods in Neural ODEs on CIFAR-10. The left panel demonstrates that TA-BN maintains high accuracy even with small batch sizes, unlike Mini-batch BN. The middle panel shows that TA-BN is more robust to noisy data. The right panel visually confirms that the statistics used in batch normalization are time-dependent in Neural ODEs.
read the caption
Figure 3: Left: We train a Neural ODE with a U-Net backbone as the learnable derivatives on CIFAR-10. Mini-batch BN shows degraded accuracies with a batch size of 2, while TA-BN can maintain high accuracies under varying batch sizes, because it uses the estimated population statistics during testing. Pop-TI BN aggregates running statistics encountered at any time points into a single pair of μ and σ². This approach assumes time-independent statistics, leading to erroneous predictions and erratic test loss curves. Middle: When noisy data exist on average in one out of every test batch, Mini-batch BN's performance deteriorates, because the noise affects the mini-batch statistics. The backbone for learnable derivatives in this experiment consists of 6 convolution layers. Right: We plot the output statistics from the first layer of U-Net over time; they are time-dependent.
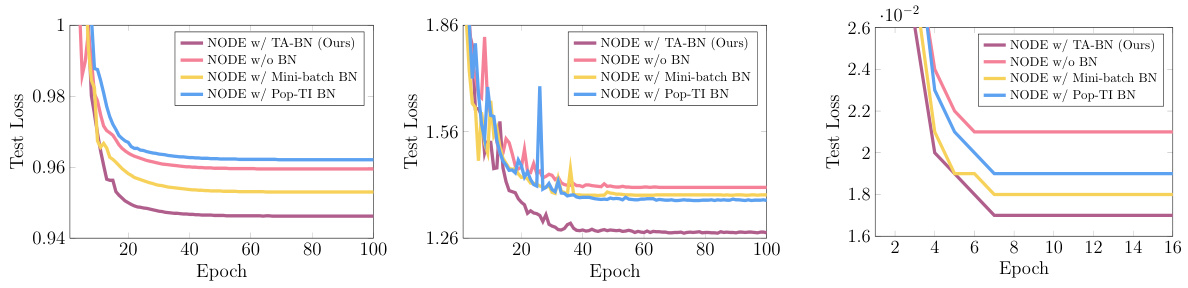
🔼 This figure compares the performance of three different batch normalization methods (TA-BN, Mini-batch BN, Pop-TI BN) and the case without batch normalization in training a Neural ODE on the CIFAR-10 dataset. The left panel demonstrates that TA-BN is robust to varying batch sizes, unlike Mini-batch BN which suffers from smaller batch sizes. Pop-TI BN, which assumes time-independent statistics, performs poorly. The middle panel shows that Mini-batch BN is sensitive to noisy data, whereas TA-BN is more robust. The right panel visualizes the time-dependent nature of the statistics generated by the Neural ODE.
read the caption
Figure 3: Left: We train a Neural ODE with a U-Net backbone as the learnable derivatives on CIFAR-10. Mini-batch BN shows degraded accuracies with a batch size of 2, while TA-BN can maintain high accuracies under varying batch sizes, because it uses the estimated population statistics during testing. Pop-TI BN aggregates running statistics encountered at any time points into a single pair of μ and σ². This approach assumes time-independent statistics, leading to erroneous predictions and erratic test loss curves. Middle: When noisy data exist on average in one out of every test batch, Mini-batch BN's performance deteriorates, because the noise affects the mini-batch statistics. The backbone for learnable derivatives in this experiment consists of 6 convolution layers. Right: We plot the output statistics from the first layer of U-Net over time; they are time-dependent.

🔼 This figure shows the test accuracy curves for Neural ODEs with varying numbers of convolutional layers (4, 8, 12, 18) as the backbone for the learnable temporal derivatives, trained on the CIFAR-10 dataset. The impact of batch normalization (BN) is also shown. The curves illustrate the relationship between model depth and training stability. The dashed lines indicate training failures, demonstrating that deeper Neural ODEs without appropriate techniques often fail to converge during training.
read the caption
Figure 1: Test accuracies are depicted over the training epochs on CIFAR-10, utilizing Neural ODEs with different numbers of convolution layers as the backbones for learnable derivatives. Dashed horizontal lines denote instances of training failures.
More on tables
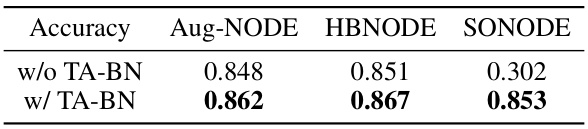
🔼 This table compares the test accuracy of three different Neural ODE variations (Aug-NODE, HBNODE, and SONODE) with and without the application of Temporal Adaptive Batch Normalization (TA-BN). It demonstrates the performance improvement achieved by incorporating TA-BN into these existing Neural ODE architectures.
read the caption
Table 2: Comparison between Neural ODE variations with and without TA-BN on CIFAR-10†.
🔼 This table compares the performance of different Neural ODE models across various datasets (MNIST, CIFAR-10, SVHN, CIFAR-100, and Tiny-ImageNet). It shows the test accuracy and the number of parameters for each model, including those using Aug-NODE, STEER, versions without batch normalization (BN), with TA-BN (the proposed method), Pop-TI BN, and Mini-batch BN. The table helps to illustrate the impact of TA-BN on model accuracy and efficiency by comparing it to various baselines. Note that ‘N/A’ indicates data not available in the original papers.
read the caption
Table 3: Comparison of test accuracies and number of parameters between different Neural ODEs†.
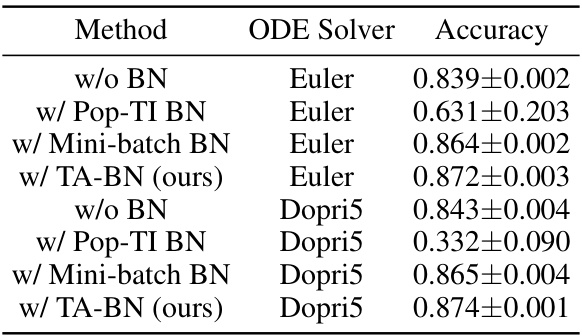
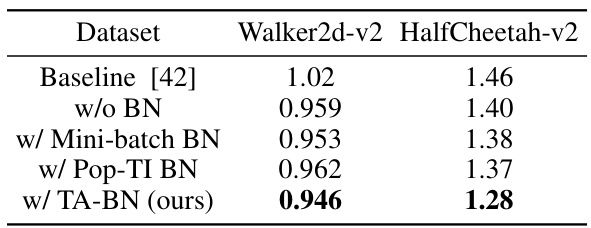
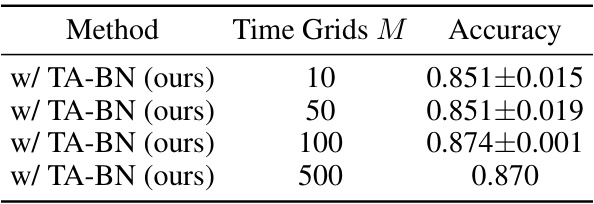
🔼 This table presents the ablation study on different ODE solvers (Euler and Dopri5) while using different batch normalization methods in a Neural ODE model. It demonstrates the impact of the ODE solver and different BN methods (w/o BN, w/ Pop-TI BN, w/ Mini-batch BN, and w/ TA-BN) on the model’s accuracy, indicating the superiority of TA-BN across various solvers.
read the caption
Table 4: Ablation study on ODE solvers.
🔼 This table compares the performance of different Neural ODE models on various image classification datasets (MNIST, CIFAR-10, SVHN, CIFAR-100, and Tiny-ImageNet). It shows the test accuracy and the number of parameters for each model. Models include those using TA-BN (Temporal Adaptive Batch Normalization), Mini-batch BN, Pop-TI BN, and no Batch Normalization. The table highlights the parameter efficiency of TA-BN, demonstrating that it achieves competitive accuracy with fewer parameters compared to other methods.
read the caption
Table 1: Comparison of test accuracies and number of parameters between different Neural ODEs†.
Full paper#