↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current graph neural networks (GNNs) heavily rely on aggregation modules, with sum-based methods being common due to their theoretical properties. However, these methods often fall short in practical applications, and more complex methods are favored. This paper investigates this gap by proposing that sum-based aggregators fail to effectively “mix” features from different neighbors, hence limiting their ability to succeed on more complex downstream tasks.
This paper introduces a new aggregation module called Sequential Signal Mixing Aggregation (SSMA). SSMA addresses the “mixing” problem by treating neighbor features as 2D signals and sequentially convolving them. The proposed method demonstrates substantial performance improvements across various benchmarks, achieving new state-of-the-art results when combined with existing GNN architectures. The theoretical analysis supports SSMA’s enhanced ability to mix features and its efficient representation size.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with graph neural networks (GNNs). It addresses limitations of existing GNN aggregation methods, presenting a novel approach called SSMA that significantly improves performance on various benchmarks. SSMA’s ability to enhance feature mixing offers a new perspective on GNN design, opening avenues for improved model expressivity and performance. This work’s impact extends to various applications using GNNs, spurring further research into advanced aggregation techniques and model architectures.
Visual Insights#

This figure illustrates how the DeepSets polynomial, originally designed for scalar features, can be generalized to handle vector features efficiently and provably. The left side shows the original DeepSets polynomial representation using scalar features (u, v, w). The right side demonstrates the generalization to vector features (u¹, u², u³, u⁴; v¹, v², v³, v⁴; w¹, w², w³, w⁴), showing how each vector is treated as a polynomial of another variable (z), allowing for a polynomial representation with a polynomial size in terms of the number of vectors and dimensionality. This efficient generalization addresses a significant limitation of the original DeepSets polynomial in handling high-dimensional data.
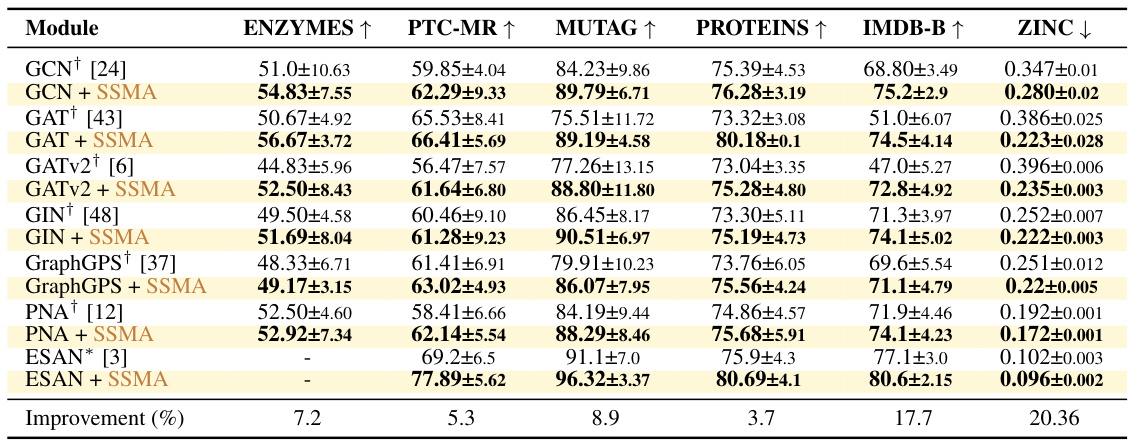
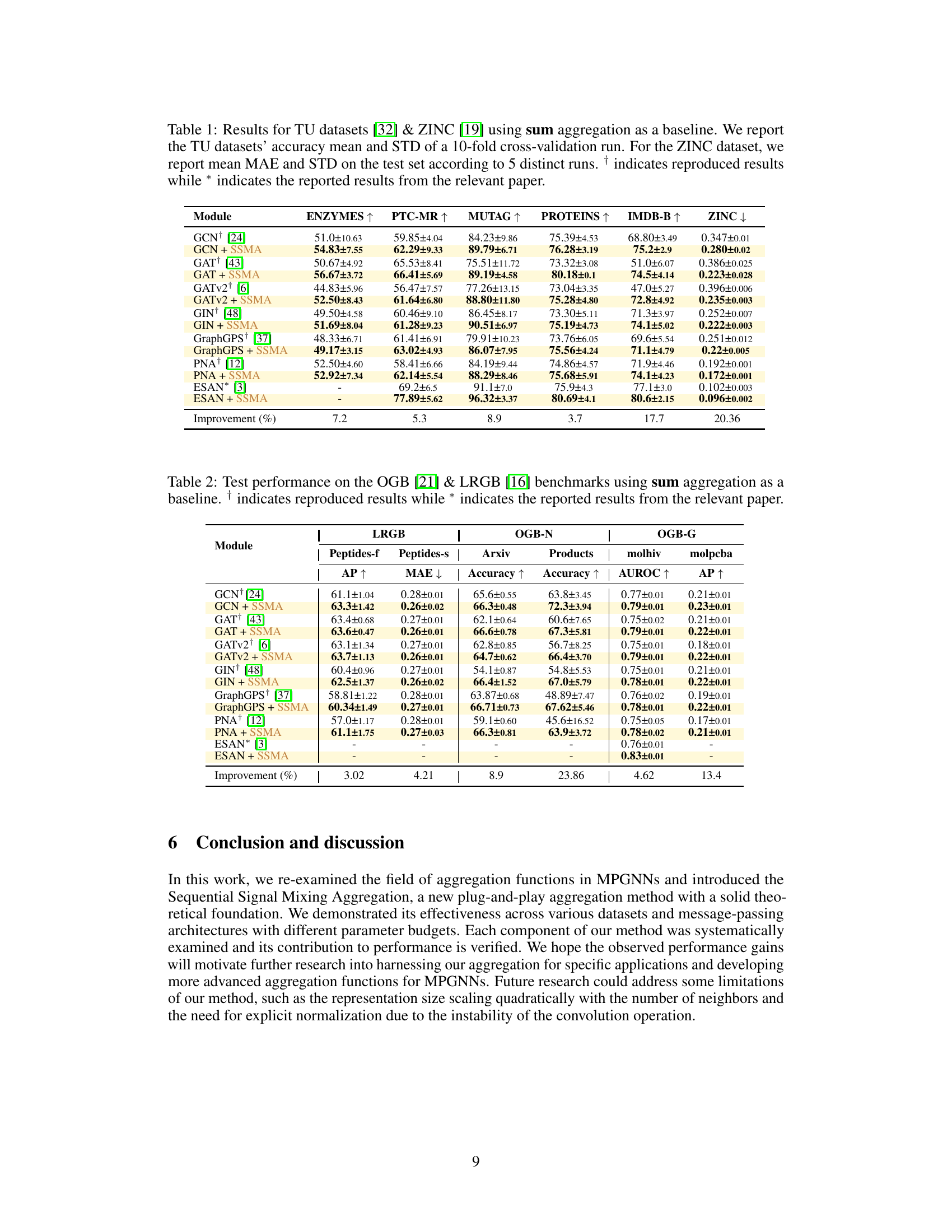
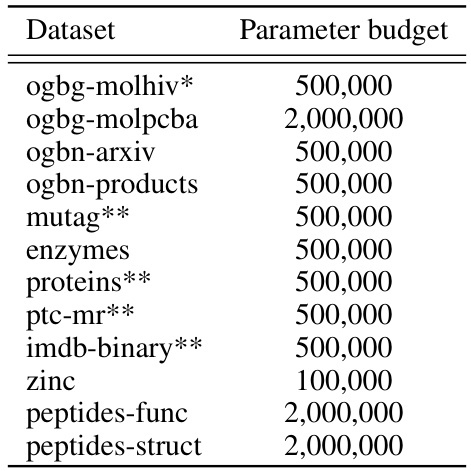
This table presents the results of experiments on several benchmark datasets using sum aggregation as a baseline. It compares the performance of various graph neural network (GNN) architectures, both with and without the proposed SSMA aggregation method. The metrics reported are accuracy (for TU datasets) and Mean Absolute Error (MAE) (for ZINC). The table shows that SSMA consistently improves performance compared to the baseline across all the datasets.
In-depth insights#
Neighbor-Mixing Issue#
The core idea of “neighbor-mixing” revolves around the limitation of sum-based aggregators in message-passing graph neural networks (MPGNNs). These aggregators, while theoretically sound in their separation capabilities, struggle to effectively combine features from distinct neighbors. This inability to mix effectively hinders performance on downstream tasks that require intricate feature interactions. The paper argues that sum-based methods essentially treat neighbor features independently before combining them, preventing the emergence of complex, mixed representations. Instead, a superior approach, Sequential Signal Mixing Aggregation (SSMA), is proposed. SSMA leverages a convolutional approach to treat neighbor features as signals, thereby promoting feature mixing through sequential convolutions, resulting in richer and more expressive representations. The emphasis on “mixing” highlights a critical weakness of simpler methods and positions SSMA as a solution that unlocks greater expressiveness in MPGNNs.
SSMA Architecture#
The Sequential Signal Mixing Aggregation (SSMA) architecture is a novel approach to feature aggregation in Message Passing Graph Neural Networks (MPGNNs). Instead of traditional sum-based aggregation, SSMA treats neighbor features as 2D discrete signals. This allows for a more expressive representation that leverages sequential convolutions to inherently mix neighbor features. The process begins with an affine transformation of neighbor features, followed by a 2D circular convolution implemented using FFTs for efficiency. A key advantage of this approach is its provable polynomial representation size, which addresses limitations of previous sum-based aggregators. Finally, the resulting signal is compressed using an MLP to a desired dimensionality for downstream tasks. The convolutional component is crucial for the ‘mixing’ of features, a limitation of sum-based aggregation that SSMA overcomes. This innovative architecture demonstrates significantly improved performance in various benchmarks by combining effective feature mixing with a computationally efficient design.
SSMA Experiments#
The hypothetical ‘SSMA Experiments’ section would likely detail the empirical evaluation of the Sequential Signal Mixing Aggregation (SSMA) method. This would involve a rigorous comparison against existing aggregation techniques across various graph neural network (GNN) architectures and benchmark datasets. Key aspects would include the selection of appropriate datasets representing diverse graph structures and complexities. The evaluation metrics would be carefully chosen to reflect the specific tasks (classification, regression, etc.) and would likely incorporate standard metrics such as accuracy, precision, recall, F1-score, and AUC. A crucial element would be a detailed analysis of the performance gains achieved by SSMA, demonstrating its superiority in scenarios demanding high neighbor mixing capabilities. The results would be presented visually (charts, tables) and statistically, including error bars and p-values to showcase significance. The discussion would then analyze the findings, explaining the reasons for superior or inferior performance under different conditions and exploring any limitations or unexpected outcomes. Crucially, the discussion should connect empirical results back to the theoretical underpinnings of SSMA, providing a cohesive narrative linking the theoretical claims to real-world performance.
SSMA Limitations#
The Sequential Signal Mixing Aggregation (SSMA) method, while demonstrating significant improvements in various graph neural network (GNN) architectures, is not without limitations. Computational cost is a primary concern, particularly with dense graphs, where the O(n²d) complexity of SSMA can be prohibitive. The reliance on circular convolution and FFT operations may also pose challenges for optimization and scalability. Furthermore, the effectiveness of SSMA depends on the ability to effectively mix features from distinct neighbors, which might not always translate to improved downstream tasks. The requirement for extensive hyperparameter tuning is another factor impacting practicality. Additionally, the theoretical analysis focuses on demonstrating the enhanced mixing capability but does not fully address the impact of other components within the GNN architecture or complex downstream tasks on overall performance. Therefore, while SSMA offers a valuable enhancement to GNNs, a comprehensive understanding of these limitations is crucial for effective implementation and further research.
Future of SSMA#
The future of Sequential Signal Mixing Aggregation (SSMA) looks promising, building upon its demonstrated success in enhancing message-passing graph neural networks (MPGNNs). Further research could focus on addressing the quadratic scaling of the representation size with the number of neighbors. This could involve exploring more efficient convolutional techniques or developing adaptive neighbor selection methods that dynamically adjust to graph density. Investigating the application of SSMA to various graph types beyond those tested in the original paper is crucial. This includes exploring its performance on dynamic graphs, temporal graphs, and attributed graphs. Another area of future exploration is combining SSMA with other advanced techniques. For example, integrating SSMA with graph attention mechanisms or graph transformers could potentially yield even greater performance improvements. Finally, a comprehensive theoretical analysis exploring the limitations and boundary conditions of SSMA is warranted. This would solidify its theoretical underpinnings and guide future development, potentially leading to new theoretical insights into the expressive power of MPGNNs.
More visual insights#
More on figures
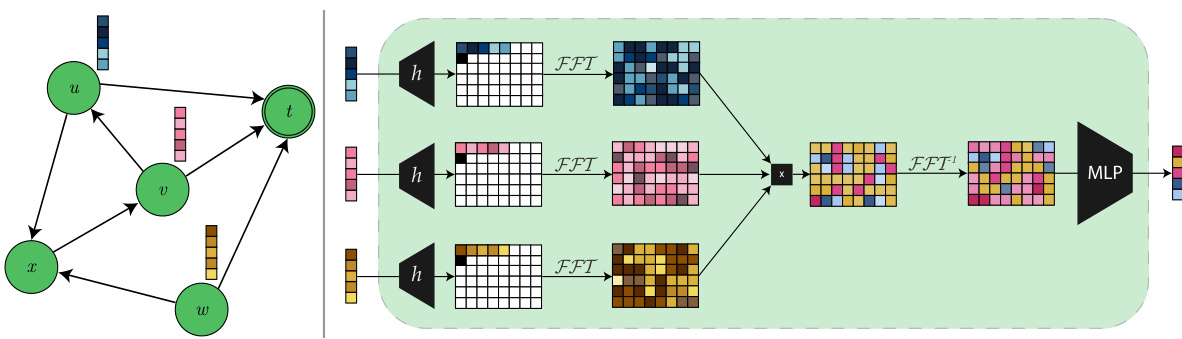
The figure visualizes the Sequential Signal Mixing Aggregation (SSMA) method. The left side shows a standard Message Passing Graph Neural Network (MPGNN) layer aggregating neighbor features. The right side illustrates the SSMA approach, which converts neighbor features into 2D signals, applies 2D circular convolution using Fast Fourier Transform (FFT) and Inverse FFT (IFFT), and finally compresses the result using a Multi-Layer Perceptron (MLP).
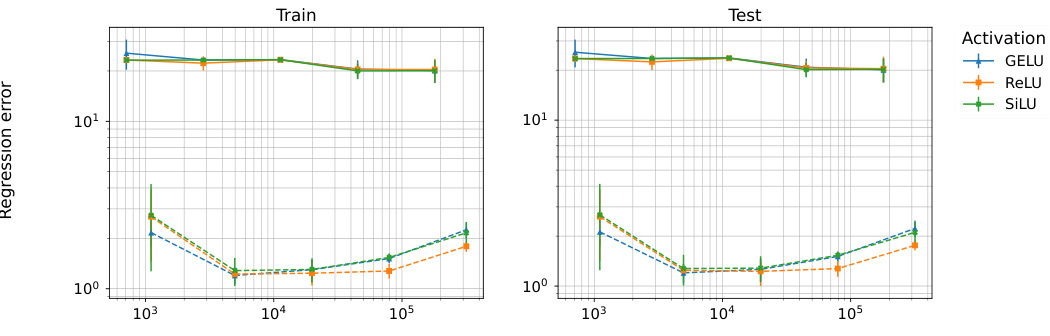
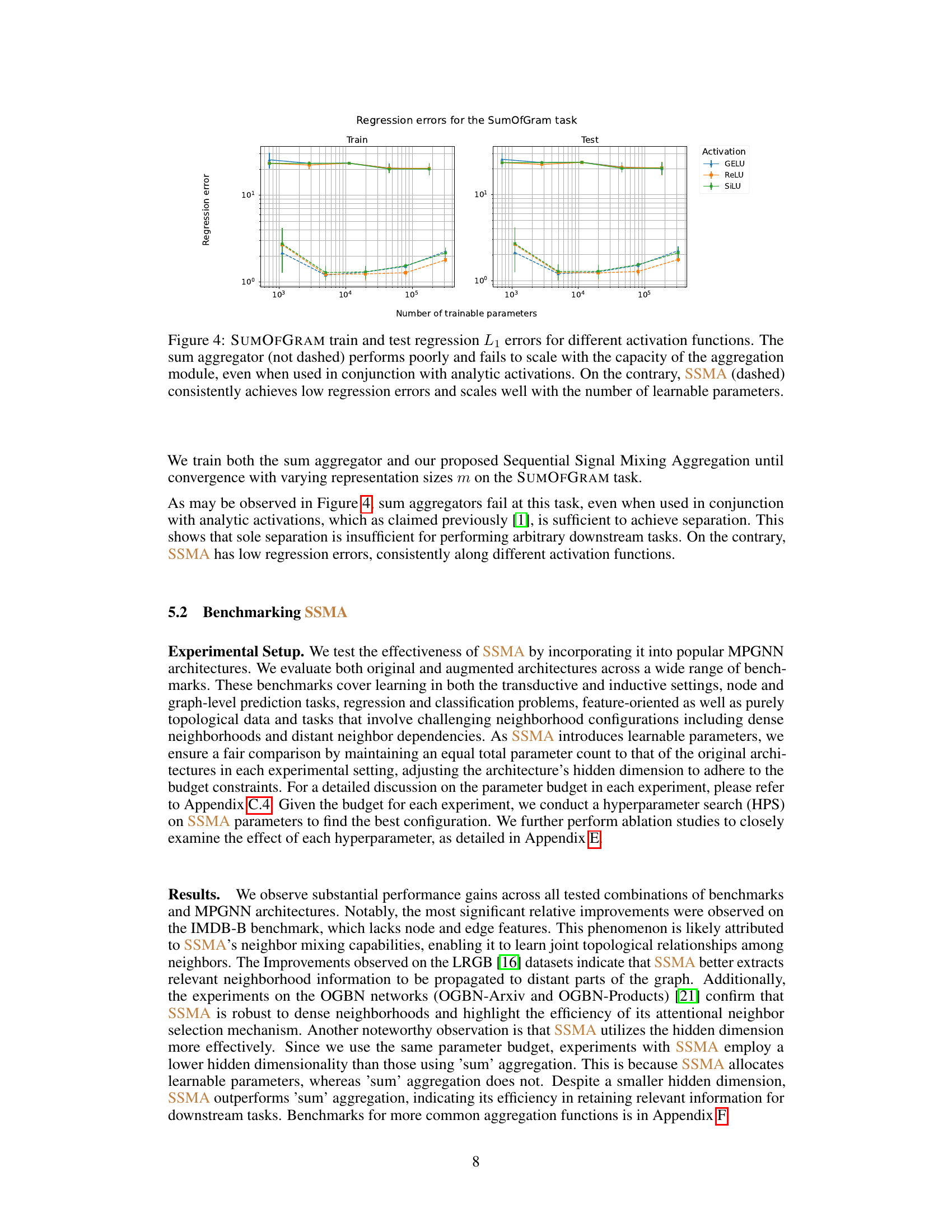
This figure compares the performance of sum-based aggregators and SSMA on the SUMOFGRAM task with different activation functions (GELU, ReLU, SILU) and varying numbers of trainable parameters. The results show that sum-based aggregators perform poorly and fail to scale, even with analytic activations known to provide theoretical separation capabilities. In contrast, SSMA consistently achieves low regression errors and scales well with increasing model size.
This figure visualizes how circular convolution in SSMA achieves higher-order neighbor mixing compared to sum-based aggregators. It shows that while sum-based aggregators only sum neighbor features, the circular convolution mixes features from distinct neighbors in a higher-order way, which is represented by the n-th order derivative calculation. This higher-order mixing ability is crucial for handling downstream tasks that require considering interactions between multiple neighbors.
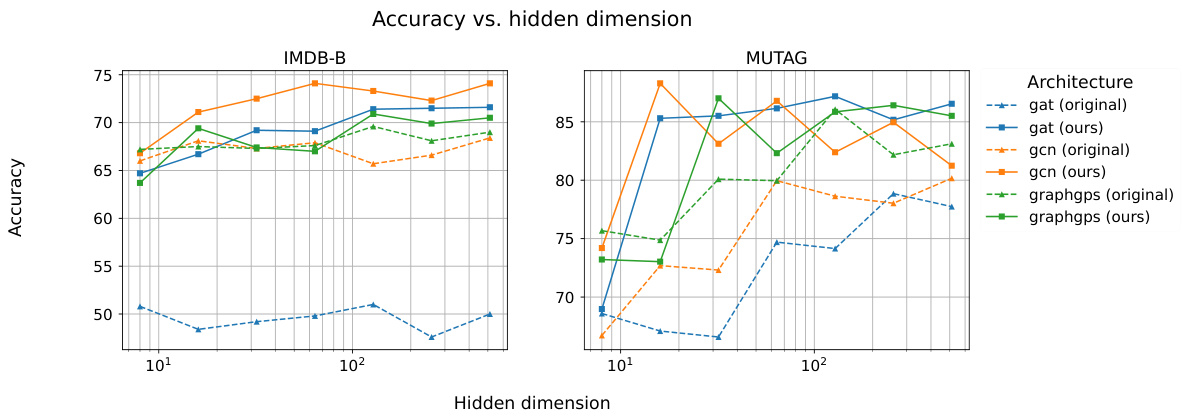
This figure shows the results of ablation studies on the IMDB-B and MUTAG datasets comparing SSMA to sum-based aggregators across various hidden dimensions and MPGNN layer types. The plots illustrate that SSMA outperforms sum-based aggregators in all parameter regimes and reaches peak performance with significantly lower hidden dimensions than its counterparts.

This figure illustrates the proposed Sequential Signal Mixing Aggregation (SSMA) method and compares it to a standard message-passing graph neural network (MPGNN) layer. The left side shows a typical MPGNN layer, aiming to create a compressed representation of a node’s neighbors. The right side details the SSMA approach, which transforms neighbor features into 2D signals, applies circular convolution using FFT and IFFT, and then compresses the result with a multi-layer perceptron (MLP).
More on tables
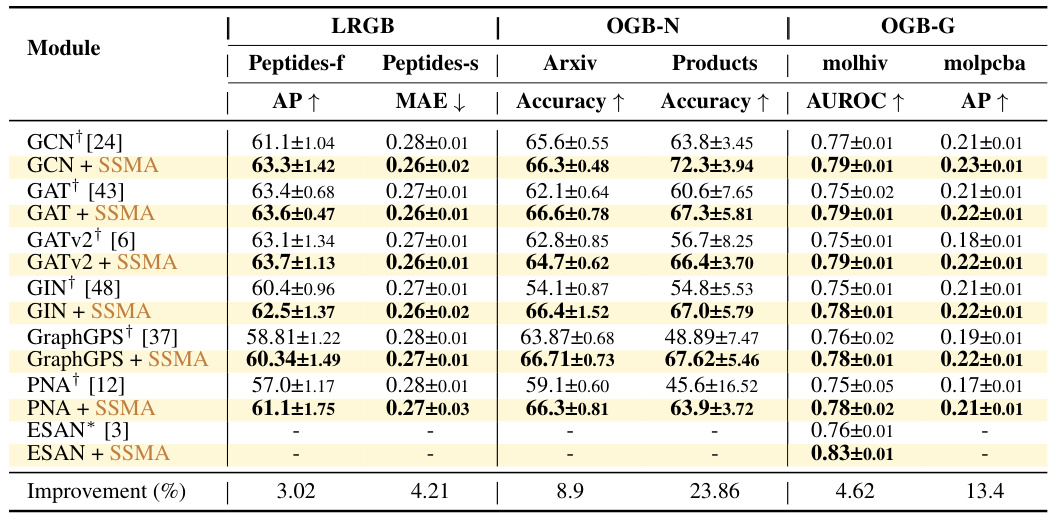
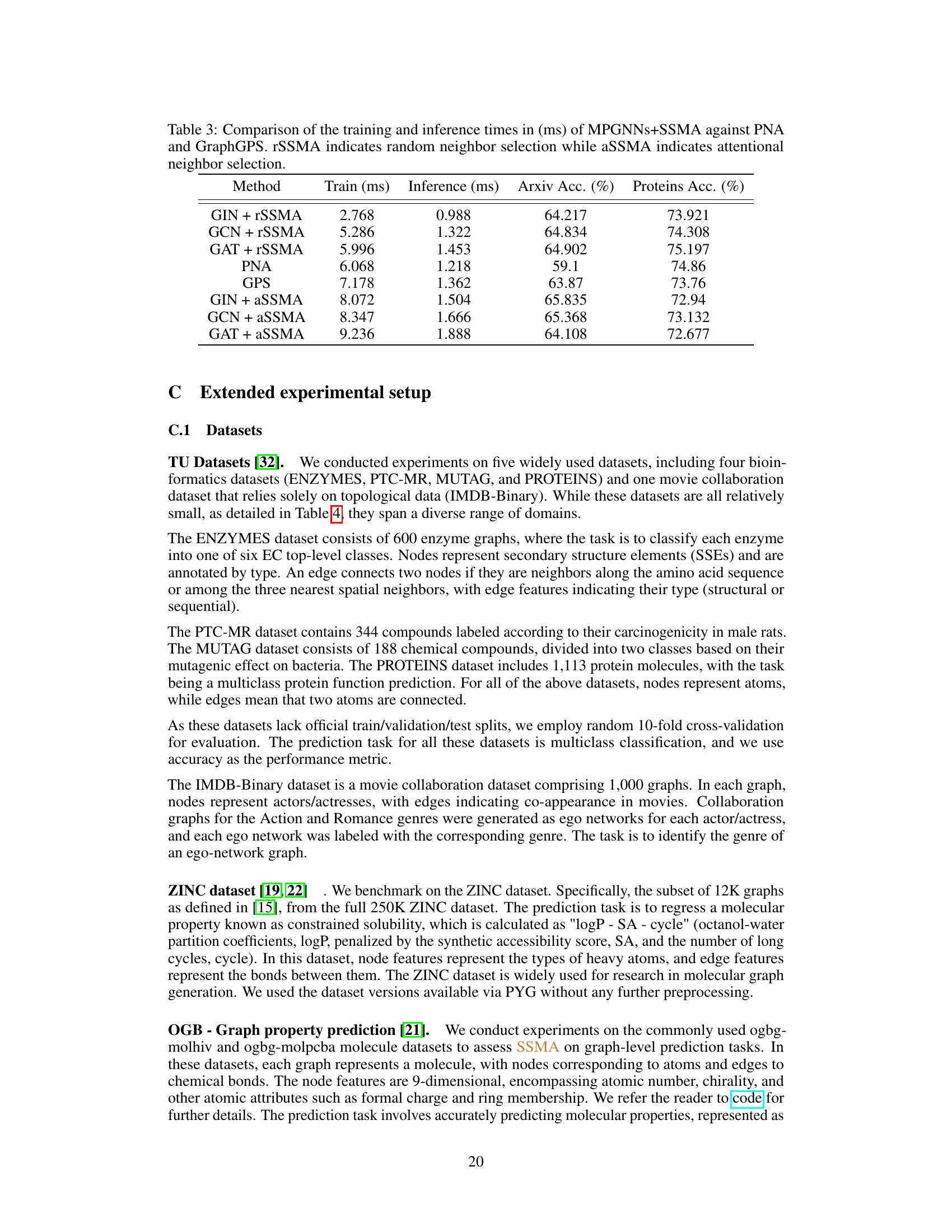
This table presents the test performance results on the Open Graph Benchmark (OGB) and Long Range Graph Benchmark (LRGB) datasets. The results are compared using sum aggregation as a baseline, with reproduced and previously reported results indicated. The table shows Average Precision (AP), Mean Absolute Error (MAE), Accuracy, and Area Under the ROC Curve (AUROC) for various graph neural network architectures with and without the Sequential Signal Mixing Aggregation (SSMA) module.
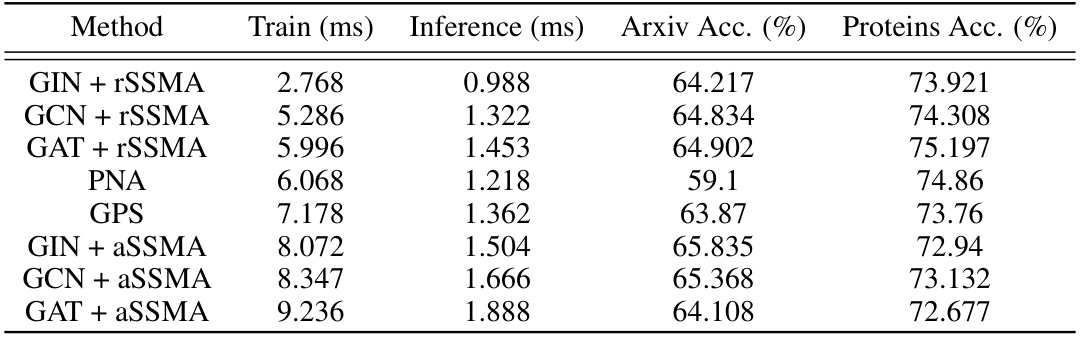
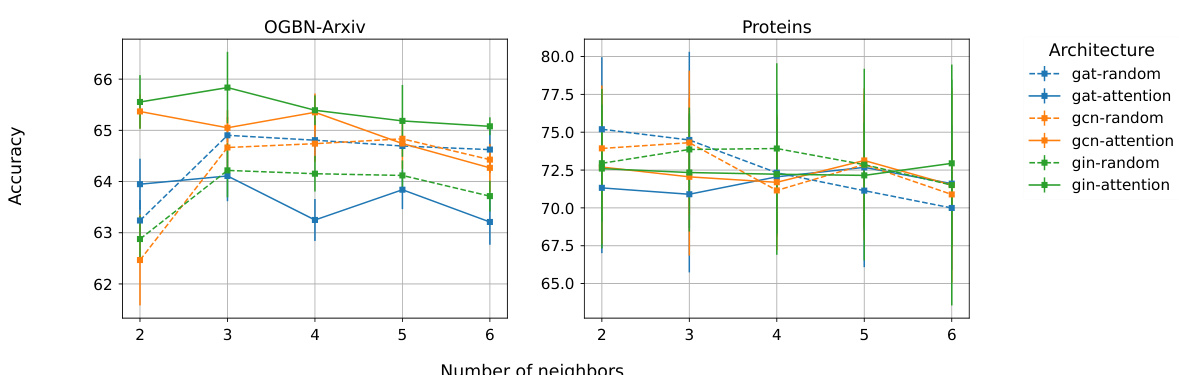
This table compares the training and inference times of several Message Passing Graph Neural Networks (MPGNNs) with and without the Sequential Signal Mixing Aggregation (SSMA) method. It also includes results from two other methods: Principal Neighbourhood Aggregation (PNA) and GraphGPS. The comparison is done for two datasets: Arxiv and Proteins, and it distinguishes between using random neighbor selection (rSSMA) and attentional neighbor selection (aSSMA). The table shows the runtimes of different models and highlights the computational efficiency of SSMA, especially the random neighbor selection version.

This table presents the results of experiments conducted on several benchmark datasets using the sum-based aggregation method as a baseline. It shows the performance of different graph neural network models (GCN, GAT, GATv2, GIN, GraphGPS, PNA, ESAN) with and without the proposed SSMA aggregation. For the TU datasets (TU datasets), accuracy (mean and standard deviation) is reported based on a 10-fold cross-validation. For the ZINC dataset, mean absolute error (MAE) and standard deviation are reported for 5 different runs. The table also includes a comparison to previously published results for some models.
This table presents the results of experiments conducted on various TU datasets and the ZINC dataset using sum aggregation as a baseline. It shows the accuracy (mean and standard deviation) for the TU datasets, obtained through 10-fold cross-validation. For the ZINC dataset, it provides the mean absolute error (MAE) and standard deviation, based on 5 independent test runs. The results are compared to previously published results where applicable, marked with † and *.

This table shows the test accuracy results for different graph neural network architectures using Variance Preserving Aggregation (VPA) and Sequential Signal Mixing Aggregation (SSMA). The results are averaged over 10-fold cross-validation runs. It demonstrates that SSMA consistently outperforms VPA across various datasets, highlighting the effectiveness of SSMA in improving model performance.
This table presents the results of experiments on several benchmark datasets (TU datasets and ZINC) comparing the performance of various Graph Neural Network (GNN) models using two different aggregation methods: sum aggregation (baseline) and the proposed Sequential Signal Mixing Aggregation (SSMA). The table shows the accuracy (for TU datasets) and Mean Absolute Error (MAE) (for ZINC) achieved by each GNN architecture with and without SSMA. The results demonstrate the improved performance of SSMA across different GNN architectures and datasets.
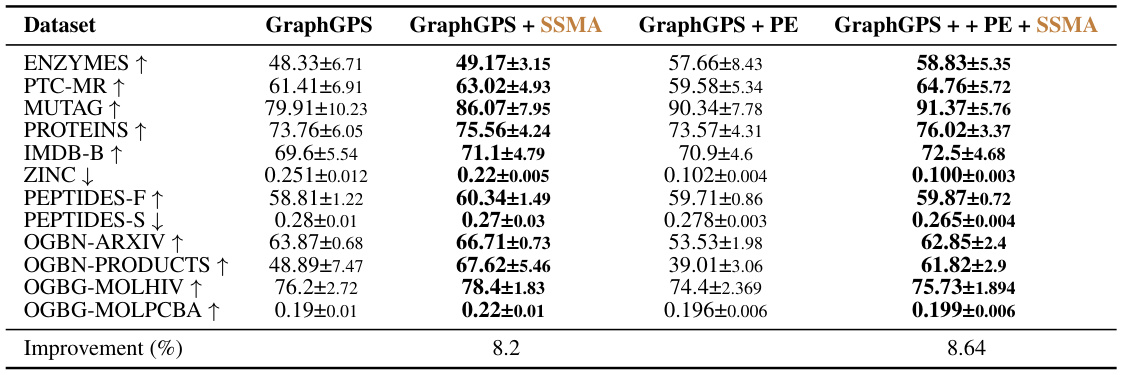
This table presents the results of experiments using GraphGPS with and without positional encoding and with the proposed SSMA aggregation method. The results are compared against the baseline GraphGPS model. The table shows the performance metrics (accuracy or MAE) for various datasets, demonstrating the impact of positional encoding and SSMA on the model’s performance.

This table presents the results of an ablation study on the ZINC dataset, comparing the performance of using a learnable affine transformation versus a constant affine transformation in the SSMA aggregation module for different GNN architectures (GCN, GAT, GIN). The numbers show mean ± standard deviation of a metric, likely Mean Absolute Error (MAE) for a property prediction task on the ZINC dataset.

This table presents the results of experiments on several graph datasets (TU datasets and ZINC) comparing different graph neural network (GNN) models with the proposed SSMA aggregation against the baseline sum aggregation. The TU datasets’ results show accuracy with standard deviation calculated over 10-fold cross-validation, while the ZINC dataset’s results show Mean Absolute Error (MAE) with standard deviation over 5 runs. The table also indicates which results were reproduced from other papers.
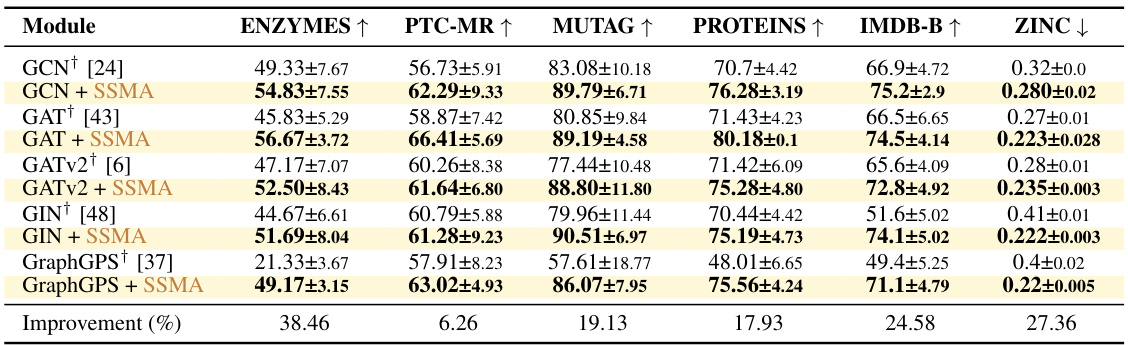
This table presents the results of experiments on several benchmark datasets using different graph neural network (GNN) architectures combined with both the standard sum aggregation and the proposed Sequential Signal Mixing Aggregation (SSMA). The TU datasets are used for node classification, while ZINC is used for regression. The table shows the accuracy (for TU datasets) or mean absolute error (MAE) (for ZINC), along with standard deviation, for each model. Results from previous research are included for comparison.
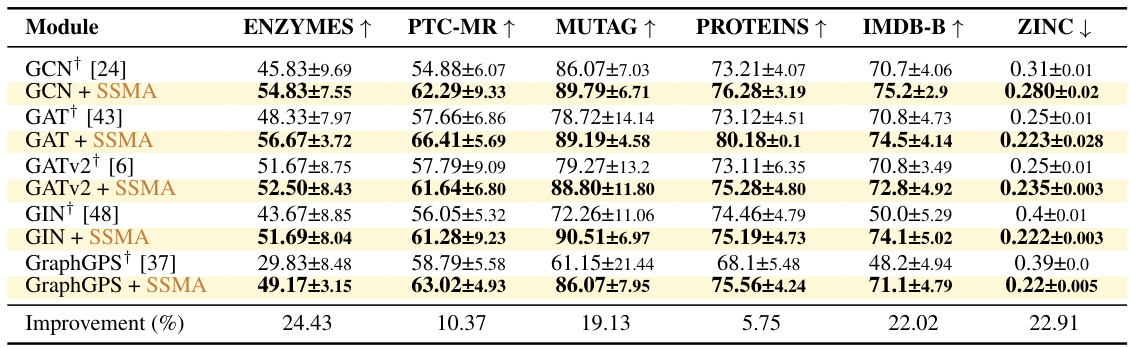
This table presents the results of experiments on various graph datasets, comparing the performance of different graph neural network architectures with and without the proposed SSMA aggregation module. The TU datasets are evaluated using 10-fold cross-validation accuracy, while ZINC is assessed using mean absolute error (MAE). The table shows that SSMA consistently improves performance across multiple network architectures and benchmarks.

This table presents the results of experiments on several benchmark datasets (TU datasets and ZINC) comparing the performance of different Graph Neural Network (GNN) architectures when using sum aggregation as a baseline. The table shows the accuracy (for TU datasets) and Mean Absolute Error (MAE) (for ZINC) achieved by various models with and without Sequential Signal Mixing Aggregation (SSMA). The results demonstrate SSMA’s effectiveness in improving GNN performance across different datasets and architectures.

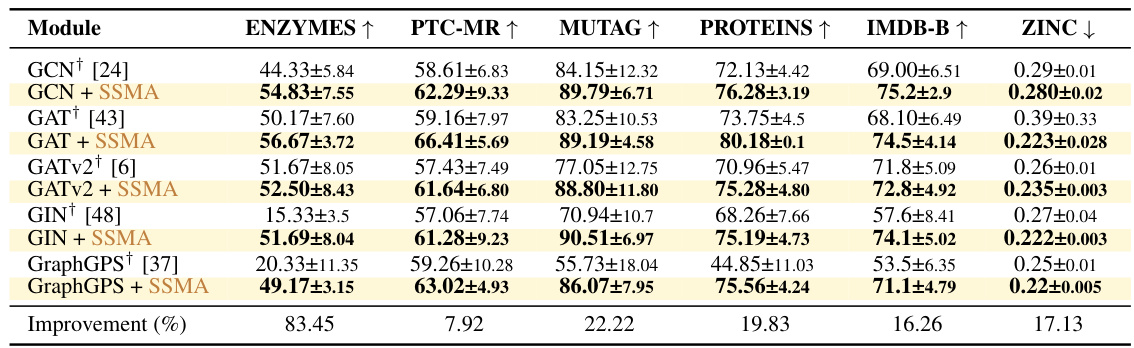
This table presents the results of experiments on various graph neural network architectures applied to several datasets. It compares the performance of the proposed SSMA method against a standard sum-based aggregation baseline. The datasets used include the TU datasets (ENZYMES, PTC-MR, MUTAG, PROTEINS, IMDB-BINARY) and the ZINC dataset. For each dataset, the table shows the mean and standard deviation of accuracy (TU datasets) or Mean Absolute Error (MAE) (ZINC dataset) achieved by different models. The ‘Improvement (%)’ row shows the percentage improvement achieved by the models with SSMA compared to their sum-based counterparts.
Full paper#