TL;DR#
Multimodal models often struggle when faced with incomplete data, leading to significant performance drops. Current methods try to forcefully align representations of incomplete data with complete counterparts which may lead to overfitting on spurious factors. This paper tackles this issue by focusing on probabilistic alignment instead of strict, deterministic alignment.
The proposed Probabilistic Conformal Distillation (PCD) method models missing data as a probability distribution. This distribution considers two main properties: extreme probability values (high probability near complete representations, low elsewhere), and geometric consistency between distributions of different samples. Extensive experiments showcase PCD’s superior performance over state-of-the-art methods on multiple benchmark datasets for both classification and segmentation tasks.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses a critical limitation of current multimodal learning methods—their vulnerability to missing modalities. By introducing a novel probabilistic approach, it offers a more robust and reliable way to handle missing data, which is crucial in many real-world applications where data may be incomplete. The probabilistic conformal distillation method could also inspire further research in developing more flexible and adaptive multimodal learning techniques. The code’s availability enhances reproducibility and facilitates further exploration and development within the research community.
Visual Insights#
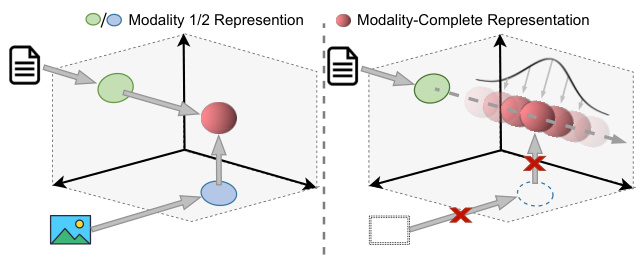
🔼 This figure illustrates the difference between modality-complete and modality-incomplete data representations in a two-modality scenario. When both modalities are available, a fused modality-complete representation is created. However, when one modality is missing, the representation derived from the remaining modality is not a single point but rather a probability distribution within the modality-complete space. This distribution is centered around the expected location of the complete representation, reflecting the uncertainty introduced by the missing data. This visualization highlights the core concept that the paper addresses: instead of enforcing a deterministic mapping between incomplete and complete representations, it’s more appropriate to model the relationship probabilistically due to inherent information asymmetry.
read the caption
Figure 1: In a two-modality scenario, when both modalities are present, the modality-complete representation is derived through fusion. When one modality is absent, the mapped representation inferred from the remaining modality is subject to a certain probability distribution in the modality-complete space.
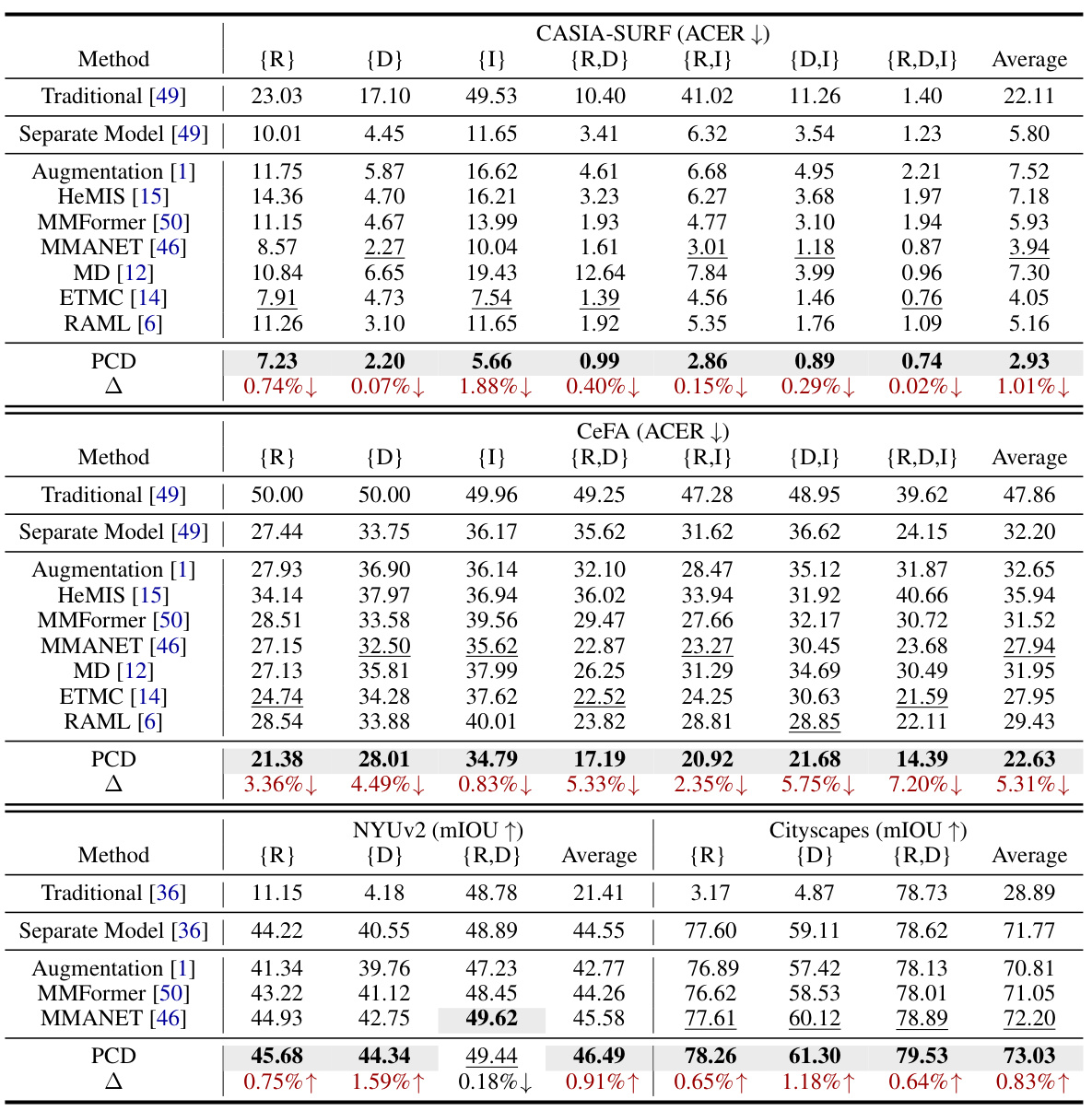
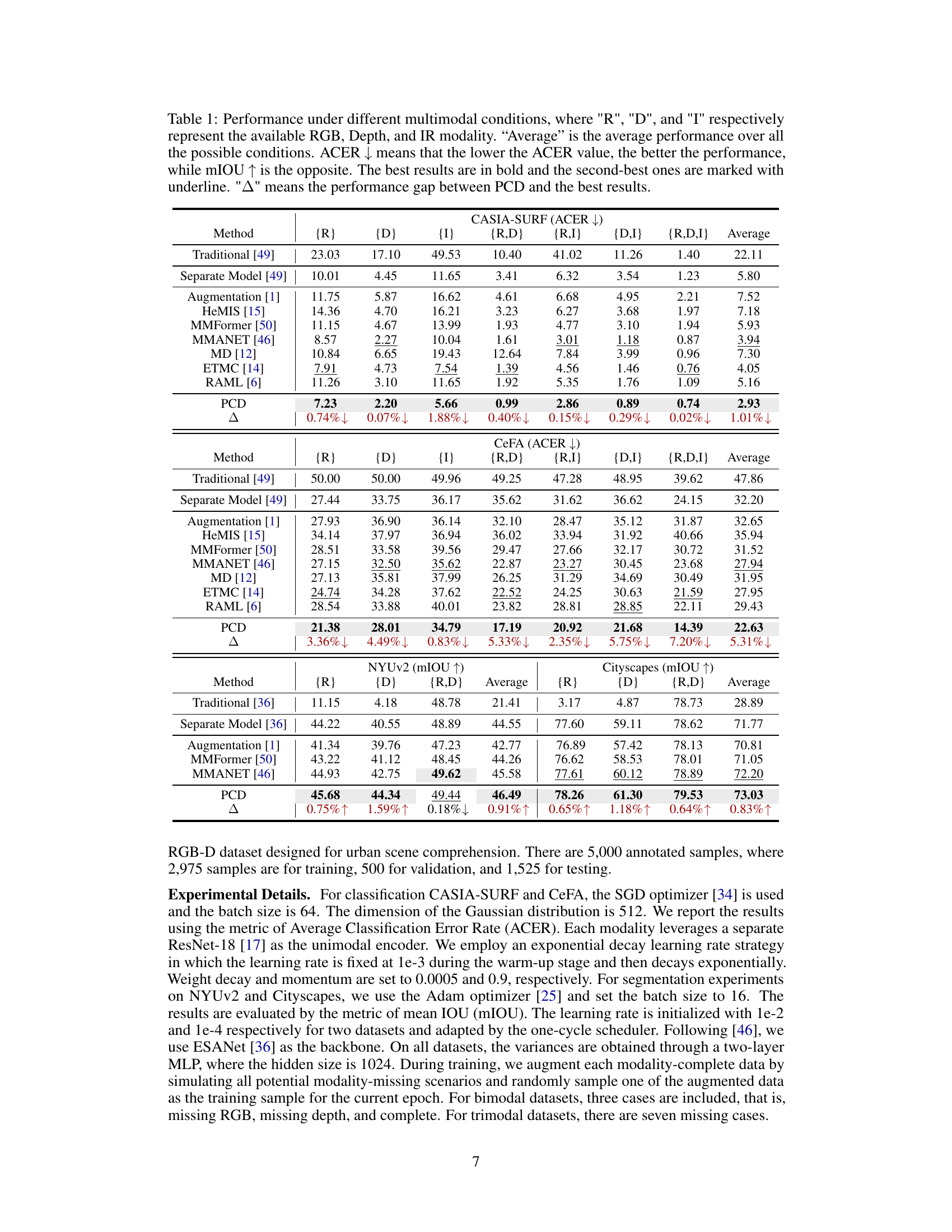
🔼 This table presents a comparison of the proposed Probabilistic Conformal Distillation (PCD) method against several state-of-the-art methods on two facial anti-spoofing datasets (CASIA-SURF and CeFA) under various missing modality scenarios. The performance is measured using Average Classification Error Rate (ACER) for classification tasks and mean Intersection over Union (mIOU) for segmentation tasks. The table highlights the superiority of the PCD method across different missing modality combinations by showing the average performance and performance for each modality combination.
read the caption
Table 1: Performance under different multimodal conditions, where 'R', 'D', and 'I' respectively represent the available RGB, Depth, and IR modality. “Average” is the average performance over all the possible conditions. ACER ↓ means that the lower the ACER value, the better the performance, while mIOU ↑ is the opposite. The best results are in bold and the second-best ones are marked with underline. '∆' means the performance gap between PCD and the best results.
In-depth insights#
Probabilistic Alignment#
Probabilistic alignment, in the context of multimodal learning, offers a robust and flexible approach to handling missing modalities. Unlike deterministic methods that force a precise correspondence between incomplete and complete data representations, probabilistic alignment acknowledges the inherent uncertainty. It models the relationship as a probability distribution, allowing the model to learn a more nuanced representation of the missing information, reducing the risk of overfitting to spurious correlations present in the complete data. This approach is particularly beneficial when the missing modality information is irretrievably lost, as it does not impose a strict, potentially erroneous, mapping but rather learns a plausible distribution over possible completions. The method’s probabilistic nature also introduces greater tolerance to noisy or incomplete data, improving the model’s overall robustness and generalization ability. Key advantages include mitigating overfitting, enhanced tolerance to data imperfections and improved generalization performance. However, careful consideration should be given to choosing the right probability distribution and its parameters to ensure effective alignment and accurate modeling of missing data. Further research may explore different probabilistic models and optimization strategies to enhance its effectiveness.
Conformal Distillation#
Conformal distillation, a novel technique in machine learning, addresses the challenge of robust multimodal learning under missing modality scenarios. Unlike traditional methods that enforce strict alignment between complete and incomplete data representations, conformal distillation models the missing modality as a probability distribution. This probabilistic approach acknowledges the inherent uncertainty in recovering missing information and avoids overfitting to spurious correlations. By focusing on the probability density function (PDF) of the mapped variables in the complete space, the method is able to learn more robust representations, and therefore enhance missing modality robustness. The framework employs a teacher-student architecture, and the student model learns to approximate the unknown PDF, satisfying two key characteristics: extreme probability points (high probabilities for close points, low for distant points in complete space) and geometric consistency (conformal relationships between PDFs of different data points). This innovative approach provides more flexibility and tolerance for missing data in multimodal learning, improving model generalization and robustness.
Missing Modality#
The concept of ‘missing modality’ in multimodal learning presents a significant challenge, as models trained on complete data often fail when faced with incomplete inputs. Robustness to missing modalities is crucial for real-world applications where data collection is imperfect. Approaches like independent modeling handle missing modalities by training separate models for each missing modality combination, but this is inefficient and lacks flexibility. Unified modeling offers a more elegant solution, employing techniques like cross-modal knowledge distillation to guide the representation of incomplete data towards alignment with its complete counterpart. However, simply forcing alignment can lead to suboptimal performance and overfitting, since it ignores the inherent information asymmetry. Probabilistic approaches offer a more nuanced way to tackle missing data, by modeling the uncertain representation as a distribution rather than a single point, thereby capturing inherent uncertainty and enhancing robustness.
Robustness Enhancement#
The concept of ‘Robustness Enhancement’ in the context of a research paper likely centers on methods to improve the reliability and stability of a model or system, particularly in the face of unforeseen circumstances or noisy data. This could involve techniques to mitigate the impact of missing modalities, a common challenge in multimodal learning. Probabilistic approaches, which account for the inherent uncertainty in incomplete data, might be a key strategy. The effectiveness of such techniques would likely be demonstrated through rigorous experimentation, perhaps comparing the performance of the enhanced model against state-of-the-art alternatives across various scenarios simulating missing data or adversarial attacks. Metrics measuring robustness are essential, providing quantitative evidence of the improvement. It also is likely that discussion of the underlying principles and theoretical justification for the enhancement methods are part of the paper. The paper might also analyze the trade-offs between robustness and other performance aspects like accuracy or efficiency. Ultimately, a successful ‘Robustness Enhancement’ section would present a compelling case for improved reliability, demonstrating practical benefits through empirical evidence and insightful analysis.
Multimodal Learning#
Multimodal learning tackles the challenge of integrating information from diverse sources, such as text, images, and audio, to achieve enhanced understanding and performance. A core strength lies in its ability to leverage complementary information from different modalities, mitigating the limitations of unimodal approaches. However, this integration introduces complexities, including the need for effective fusion strategies to combine data representations and the handling of missing modalities. Robustness is a major concern, as the presence or absence of certain modalities can significantly impact model accuracy. Research focuses on developing efficient and flexible methods for data fusion, as well as techniques for dealing with the inherent uncertainty and noise in multimodal data. This field holds significant promise for applications in various domains such as computer vision, natural language processing, and healthcare. Furthermore, the development of effective training methodologies is crucial for success, given the complexity of optimizing models with data from multiple sources.
More visual insights#
More on figures
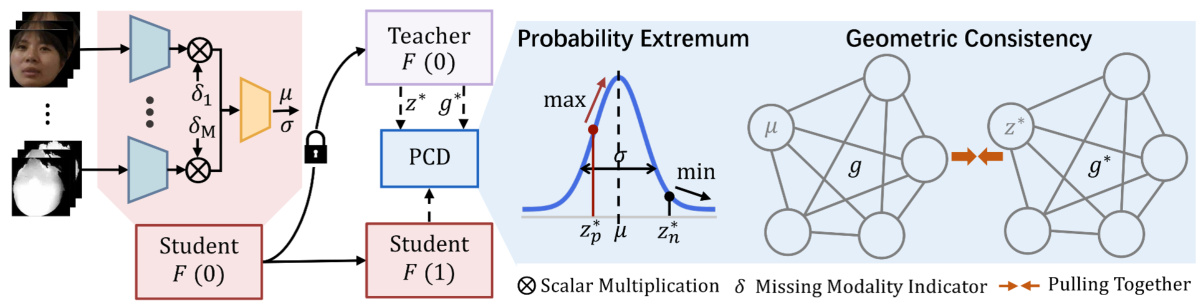
🔼 This figure illustrates the PCD framework, a self-knowledge distillation (self-KD) architecture. The teacher network, using complete modality data, provides the modality-complete feature vector (z*) and geometric structure (g*) as guidance. The student network, handling modality-missing data, models the missing features as probabilistic distributions (using Gaussian distributions). The objective is twofold: maximize the probability for points close to the complete data (z*) and minimize it for distant points (z*), while ensuring geometric consistency between the student’s structure (g) and the teacher’s structure (g*).
read the caption
Figure 2: An overview of the proposed method. PCD is a self-KD architecture, where the teacher and student share the same framework. The teacher provides the modality-complete feature z* and the geometric structure g* to guide the student. In the student, modality-missing features are parameterized as different normal distributions to fit the corresponding PDF. To achieve this, PCD maximizes distributions at positive z and minimizes it at z, while aligning g with positive g*.

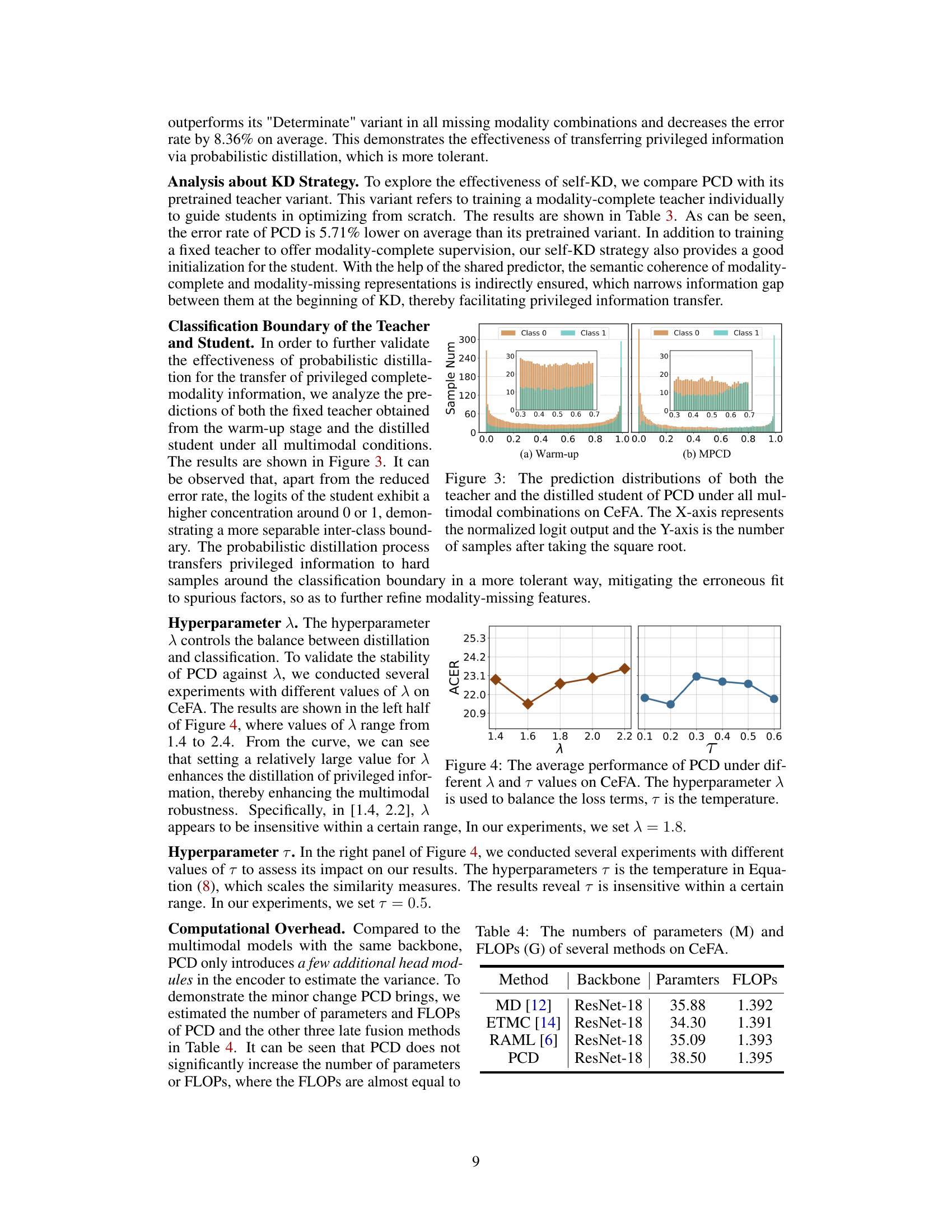
🔼 This figure visualizes the prediction distributions of both the teacher and student models trained using PCD on the CeFA dataset. The plots show the normalized logit outputs (x-axis) against the square root of the sample counts (y-axis), separated by class (Class 0 and Class 1). The comparison highlights how PCD improves the clarity of the classification boundary by increasing the separation between the two classes, as evidenced by the concentration of the student’s logits closer to 0 or 1.
read the caption
Figure 3: The prediction distributions of both the teacher and the distilled student of PCD under all multimodal combinations on CeFA. The X-axis represents the normalized logit output and the Y-axis is the number of samples after taking the square root.

🔼 This figure shows the performance of the PCD model on the CeFA dataset under different values of hyperparameters λ and τ. The hyperparameter λ balances the probability extremum loss and the geometric consistency loss, while τ is a temperature parameter in the contrastive learning component that affects the similarity measure. The figure indicates that PCD shows relatively stable performance across a range of λ values between 1.4 and 2.2 and τ values between 0.1 and 0.6, although there is a slight peak in performance within those ranges.
read the caption
Figure 4: The average performance of PCD under different λ and τ values on CeFA. The hyperparameter λ is used to balance the loss terms, τ is the temperature.

🔼 This figure visualizes the distributions of modality-complete features and individual modality features (RGB, Depth, and IR) obtained from a unified model without probabilistic conformal distillation. It shows how the distributions of the individual modalities differ from, but remain similar to, the distribution of the complete modality features. This similarity supports the paper’s argument that modality-missing features are probabilistically related to the complete feature representation, rather than deterministically aligned. The differences in distributions highlight the inherent indeterminacy in the mapping from incomplete to complete representations, justifying the use of probabilistic methods like the proposed PCD.
read the caption
Figure 5: The visualization of the distributions of the modality-complete, RGB, Depth, and IR representations from the unified model without distillation.

🔼 This figure shows the impact of hyperparameters λ and τ on the performance of the Probabilistic Conformal Distillation (PCD) method. The left panel shows the average performance of PCD across a range of λ values on the CASIA-SURF and CeFA datasets. The right panel shows the average performance of PCD across a range of τ values on the same datasets. The plots demonstrate the stability of PCD across a range of hyperparameter values, indicating robustness to hyperparameter tuning.
read the caption
Figure 6: The average performance of PCD under different λ and τ values on CASIA-SURF and CeFA.
More on tables

🔼 This table presents the ablation study results performed on the CeFA dataset to analyze the impact of each loss component (probability extremum loss (Lu), geometric consistency loss (Lg), and task loss (Lc)) on the classification performance. It shows the average ACER (Authentication Classification Error Rate) across various modality-missing scenarios for different combinations of included loss terms. The results demonstrate the contribution of each loss component and highlight the optimal combination for best performance.
read the caption
Table 2: Ablation study on CeFA. × and √ in the table indicate without and with the corresponding loss term respectively.

🔼 This table presents a comparison of the performance of three different methods on the CeFA dataset, a multimodal classification dataset. The methods compared are PCD (Probabilistic Conformal Distillation), a ‘Determinate’ variant of PCD using a deterministic distillation method, and a ‘Pretrained’ version using a pretrained teacher. The results are broken down by missing modality configurations. It shows how the probabilistic approach of PCD, and its specific design choices, affects the performance in different scenarios of missing modalities.
read the caption
Table 3: The comparison between PCD and its variants on CeFA, where 'Determinate' means the degradation of PCD with determinate distillation, while 'Pretrained' is the distillation with a pretrained teacher.
🔼 This table presents the performance comparison of different methods under various missing modality scenarios on two datasets (CASIA-SURF and CeFA). The table shows the Average Classification Error Rate (ACER) for different combinations of available modalities (RGB, Depth, IR). Lower ACER values indicate better performance. The table also shows the performance gap between the proposed method (PCD) and the best performing method for each scenario.
read the caption
Table 1: Performance under different multimodal conditions, where 'R', 'D', and 'I' respectively represent the available RGB, Depth, and IR modality. “Average” is the average performance over all the possible conditions. ACER ↓ means that the lower the ACER value, the better the performance, while mIOU ↑ is the opposite. The best results are in bold and the second-best ones are marked with underline. 'A' means the performance gap between PCD and the best results.

🔼 This table presents a comparison of the proposed PCD method against several state-of-the-art methods on two face anti-spoofing datasets (CASIA-SURF and CeFA) under various missing modality scenarios. The results are shown in terms of Average Classification Error Rate (ACER) for classification and mean Intersection over Union (mIOU) for segmentation. The table highlights PCD’s superior performance and robustness across different missing modality combinations.
read the caption
Table 1: Performance under different multimodal conditions, where 'R', 'D', and 'I' respectively represent the available RGB, Depth, and IR modality. “Average” is the average performance over all the possible conditions. ACER ↓ means that the lower the ACER value, the better the performance, while mIOU ↑ is the opposite. The best results are in bold and the second-best ones are marked with underline. 'A' means the performance gap between PCD and the best results.

🔼 This table presents a comparison of the proposed PCD method against several state-of-the-art methods across various multimodal scenarios on two datasets, CASIA-SURF and CeFA. The table details the performance (ACER for classification, mIOU for segmentation) under different combinations of available modalities (RGB, Depth, IR). The average performance across all modality combinations is also provided, along with the performance difference between PCD and the best-performing method.
read the caption
Table 1: Performance under different multimodal conditions, where 'R', 'D', and 'I' respectively represent the available RGB, Depth, and IR modality. “Average” is the average performance over all the possible conditions. ACER ↓ means that the lower the ACER value, the better the performance, while mIOU ↑ is the opposite. The best results are in bold and the second-best ones are marked with underline. 'A' means the performance gap between PCD and the best results.
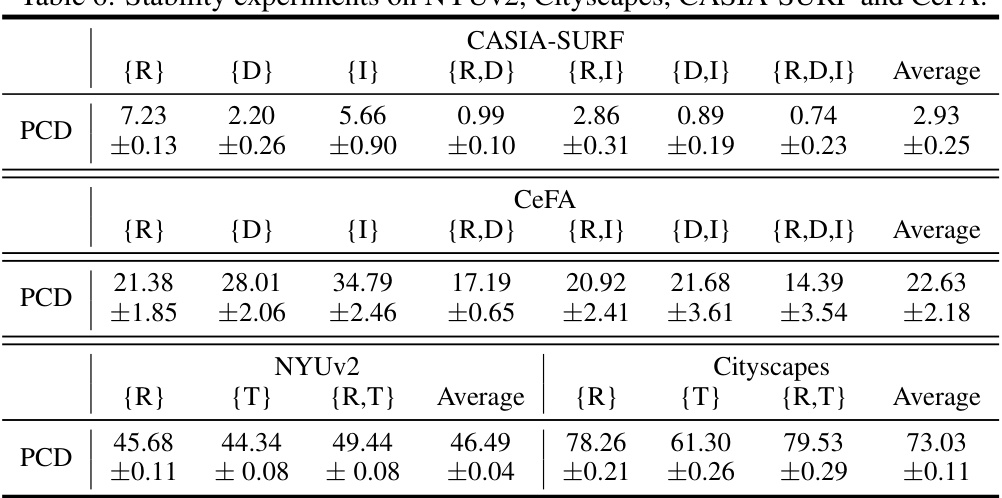
🔼 This table presents a comparison of the proposed Probabilistic Conformal Distillation (PCD) method against several state-of-the-art methods on two face anti-spoofing datasets (CASIA-SURF and CeFA). The performance is evaluated under various conditions of missing modalities (RGB, Depth, and IR), showing ACER (for classification). The table highlights the superior performance of PCD across different scenarios of missing modalities, demonstrating its robustness to incomplete data.
read the caption
Table 1: Performance under different multimodal conditions, where 'R', 'D', and 'I' respectively represent the available RGB, Depth, and IR modality. “Average” is the average performance over all the possible conditions. ACER ↓ means that the lower the ACER value, the better the performance, while mIOU ↑ is the opposite. The best results are in bold and the second-best ones are marked with underline. 'Δ' means the performance gap between PCD and the best results.

🔼 This table presents a comparison of the proposed PCD method against several state-of-the-art methods for handling missing modalities in multimodal classification and segmentation tasks. The performance is evaluated under various missing modality scenarios (RGB, Depth, IR, and combinations thereof) for two classification datasets (CASIA-SURF and CeFA) and two segmentation datasets (NYUv2 and Cityscapes). The metrics used are Average Classification Error Rate (ACER) for classification and mean Intersection over Union (mIOU) for segmentation. The table highlights the superior performance of PCD in most cases across different datasets and missing modality conditions.
read the caption
Table 1: Performance under different multimodal conditions, where 'R', 'D', and 'I' respectively represent the available RGB, Depth, and IR modality. “Average” is the average performance over all the possible conditions. ACER ↓ means that the lower the ACER value, the better the performance, while mIOU ↑ is the opposite. The best results are in bold and the second-best ones are marked with underline. 'A' means the performance gap between PCD and the best results.

🔼 This table presents a comparison of the proposed PCD method against other state-of-the-art methods for handling missing modalities in multimodal classification tasks. It shows the performance (ACER) of each method across various scenarios with different missing modalities (RGB, Depth, IR) on two datasets, CASIA-SURF and CeFA. The average performance across all scenarios is also included. Lower ACER scores are better.
read the caption
Table 1: Performance under different multimodal conditions, where 'R', 'D', and 'I' respectively represent the available RGB, Depth, and IR modality. “Average” is the average performance over all the possible conditions. ACER ↓ means that the lower the ACER value, the better the performance, while mIOU ↑ is the opposite. The best results are in bold and the second-best ones are marked with underline. 'A' means the performance gap between PCD and the best results.

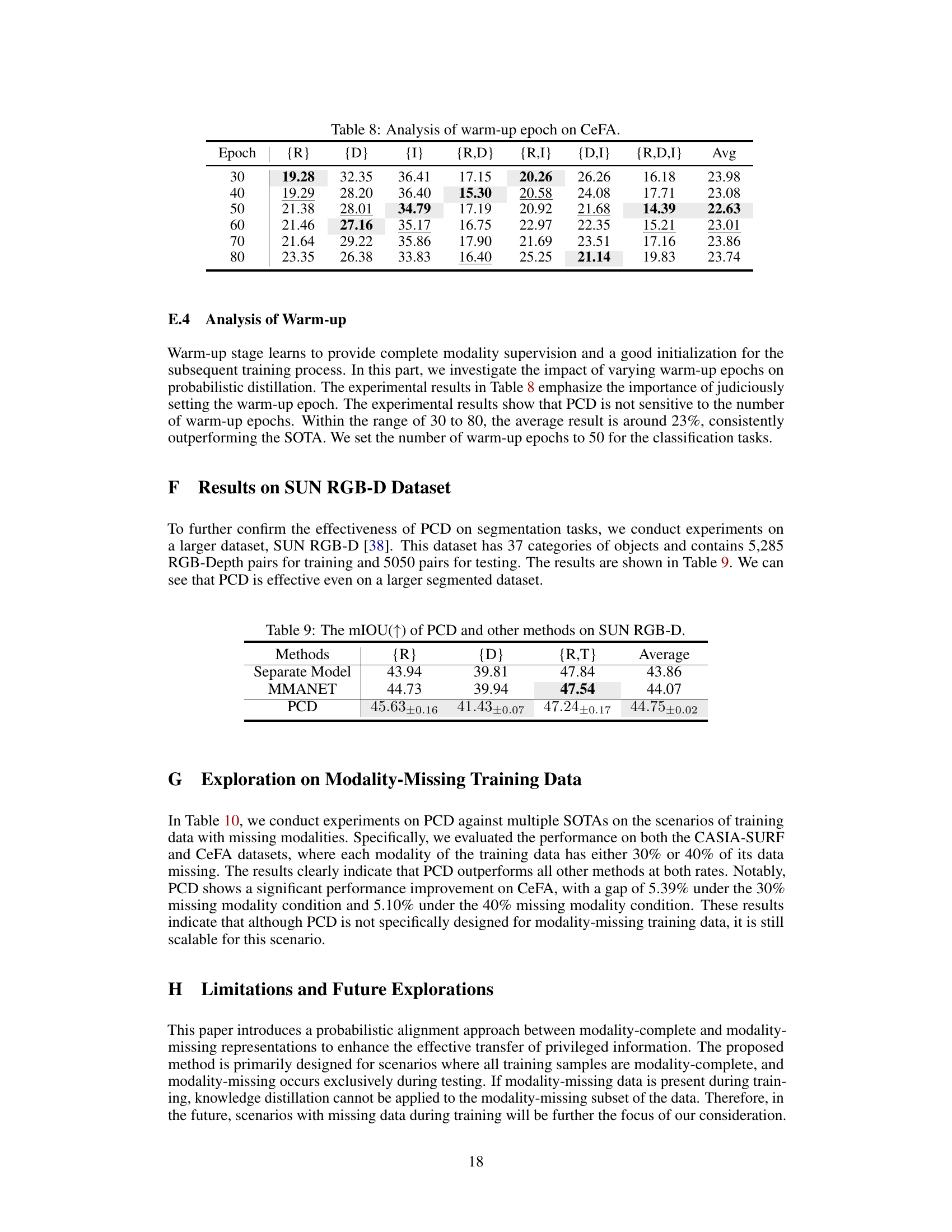
🔼 This table presents a comparison of the mean Intersection over Union (mIOU) scores achieved by different methods on the SUN RGB-D dataset for image segmentation under various modality conditions. The methods compared include a separate model approach (which trains separate models for each modality combination), MMANET (a state-of-the-art multimodal method), and the proposed PCD method. The mIOU scores are presented for when only the RGB modality is available, when only the Depth modality is available, when both RGB and Depth modalities are available, and the average mIOU across all scenarios. The results show PCD’s superior performance over other methods.
read the caption
Table 9: The mIOU(↑) of PCD and other methods on SUN RGB-D.

🔼 This table presents a comparison of the proposed PCD method against several state-of-the-art methods for handling missing modalities in multimodal classification and segmentation tasks. It shows the performance (measured by ACER for classification and mIOU for segmentation) across different missing modality scenarios (R, D, I representing RGB, Depth, and Infrared modalities). The table highlights PCD’s superior performance compared to other methods in most conditions and provides the difference between PCD’s performance and the best performing method for each scenario.
read the caption
Table 1: Performance under different multimodal conditions, where 'R', 'D', and 'I' respectively represent the available RGB, Depth, and IR modality. “Average” is the average performance over all the possible conditions. ACER ↓ means that the lower the ACER value, the better the performance, while mIOU ↑ is the opposite. The best results are in bold and the second-best ones are marked with underline. 'A' means the performance gap between PCD and the best results.
Full paper#