↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Molecular conformer generation is a crucial yet challenging task in computational drug discovery. Current methods, such as large transformer models or those based on diffusing over torsion angles, often suffer from computational expense or limitations in accuracy and diversity. Furthermore, generating physically plausible conformers is still a major challenge in the field. Existing methods often involve complex internal calculations and large architectures, making them computationally expensive and less scalable.
ET-Flow tackles these challenges with a well-designed flow matching approach combined with equivariance and a harmonic prior. This innovative method avoids complex geometric calculations, resulting in a simpler, more scalable, and faster approach. The direct operation on all-atom coordinates with minimal assumptions leads to significant improvements in the precision and physical validity of generated conformers. ET-Flow achieves state-of-the-art performance with fewer parameters and faster inference times compared to existing methods. The increased speed and accuracy have the potential to significantly accelerate drug discovery and materials science research.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in computational drug discovery and cheminformatics because it presents a novel, efficient, and accurate method for generating molecular conformers. The method’s speed and accuracy improve upon existing methods, potentially accelerating drug discovery and materials science research. The approach opens up new avenues for investigation in equivariant networks and flow-matching techniques.
Visual Insights#

Figure 1(a) illustrates the ET-Flow’s core idea: generating molecular conformations by learning a conditional vector field that maps samples from a simple harmonic prior (x0) to samples from a data distribution (x1) via a smooth, conditional probability path. It involves rotational alignment of x0 and x1 to shorten the path for efficient computation, minimizing transport costs. Figure 1(b) shows the ET-Flow architecture, highlighting the representation module (based on TorchMD-NET) and the equivariant vector output layer that outputs the vector field.
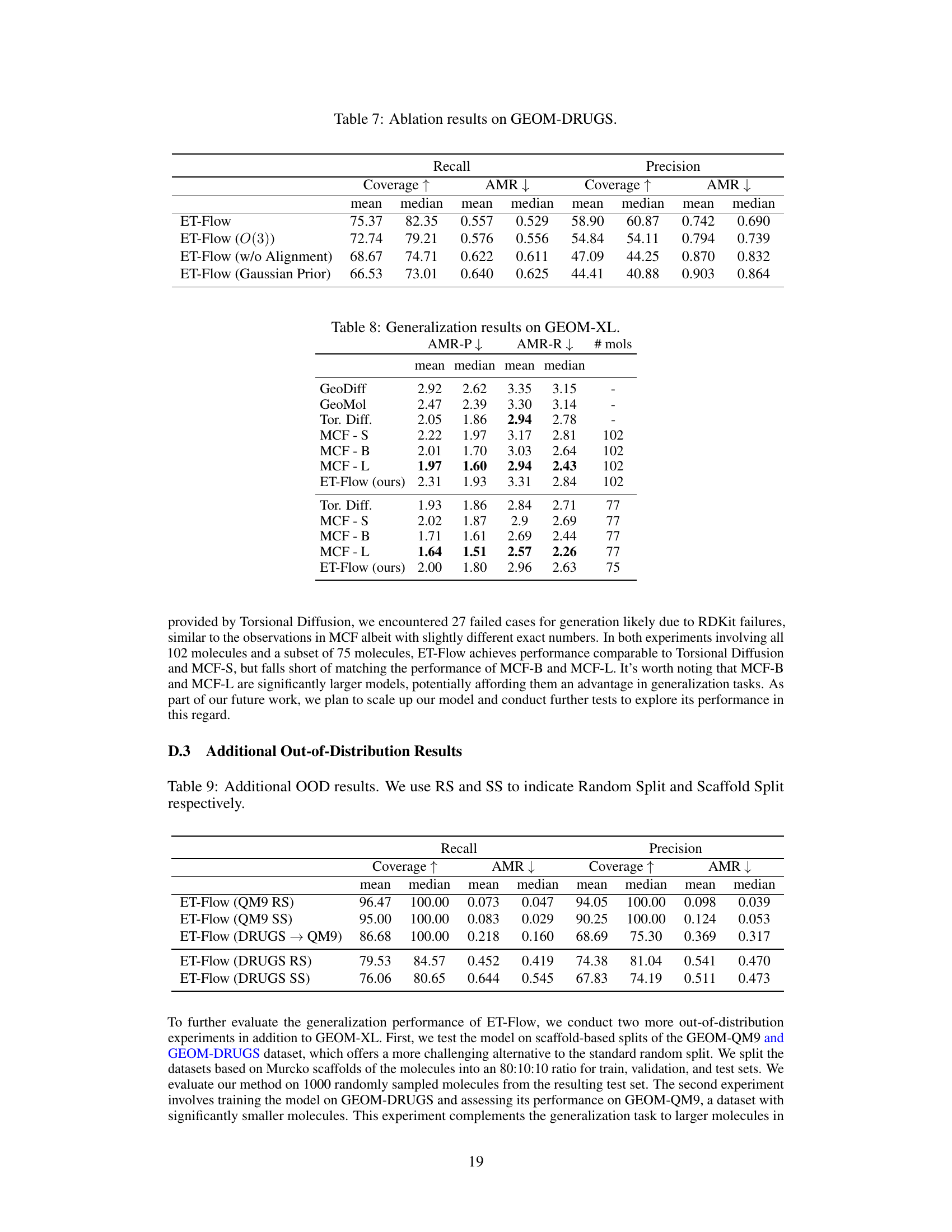
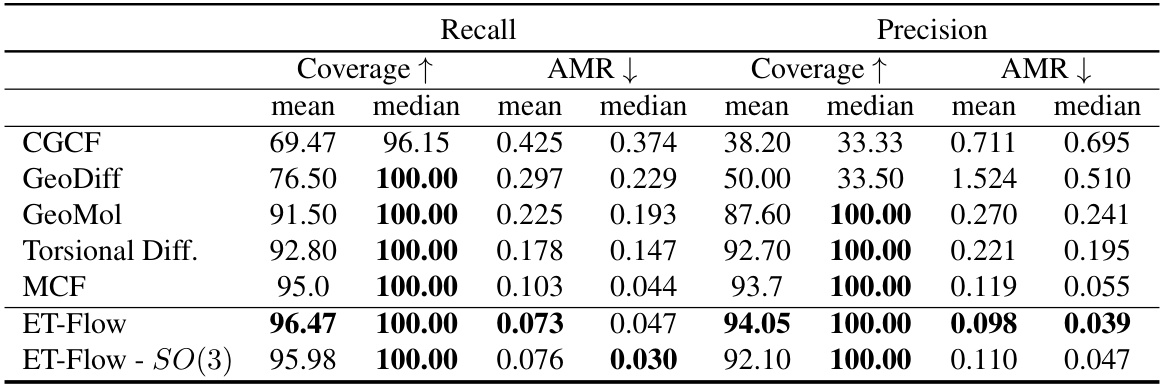
This table presents the results of molecular conformer generation experiments using different methods on the GEOM-DRUGS dataset. It compares the performance of ET-Flow (with and without stochastic sampling and SO(3) architecture for chirality correction) against several state-of-the-art baselines (GeoDiff, GeoMol, Torsional Diffusion, MCF with varying model sizes). The metrics used to evaluate performance include coverage and average minimum RMSD (AMR), both for recall and precision. The table highlights the superior performance of ET-Flow, particularly its high precision and competitive recall in comparison to the baselines.
In-depth insights#
Equivariant Flows#
Equivariant flows represent a powerful advancement in generative modeling, particularly within the context of molecular conformer generation. By incorporating equivariance, these models inherently respect the symmetries present in molecular structures, leading to more physically realistic and accurate predictions. This is a crucial improvement over traditional methods that often struggle to capture these symmetries correctly. Flow-based approaches offer significant advantages over diffusion models in terms of computational efficiency and sample quality, enabling faster inference and higher-fidelity conformer generation. The combination of equivariance and flows directly addresses the challenge of generating diverse, yet physically valid, molecular structures, thus paving the way for more accurate and efficient simulations and drug discovery applications.
Flow Matching#
The concept of ‘Flow Matching’ presents a powerful alternative to traditional diffusion models for generative tasks, particularly in complex domains like molecular conformer generation. It elegantly sidesteps the challenges of score-based diffusion by directly learning a mapping between probability distributions. This mapping is expressed as a vector field, facilitating efficient sampling without the need for lengthy iterative processes inherent in diffusion. The method’s strength lies in its flexibility, accommodating arbitrary probability paths, unlike diffusion’s restriction to specific diffusion paths. Equivariance, often incorporated with flow matching, enhances the physical validity of generated samples by ensuring that the generated conformations respect symmetries inherent in the underlying system. The integration of flow matching with equivariant transformations promises a robust and efficient approach to address complex generative modeling problems, leading to a faster training process and more physically plausible results, making it an especially promising method for applications in scientific domains.
Harmonic Priors#
Employing harmonic priors in molecular conformer generation offers a powerful inductive bias. By assuming that atoms connected by bonds should be in close proximity, harmonic priors significantly reduce the search space and improve sampling efficiency, guiding the generative model toward physically plausible conformations. This prior knowledge helps to alleviate the computational cost associated with exploring vast conformational landscapes, enabling faster and more accurate generation of low-energy conformers. The effectiveness of harmonic priors is particularly apparent when coupled with other techniques like flow matching and equivariance, leading to enhanced precision and sample diversity in the generated molecular structures. The choice of prior distribution and its incorporation within the model architecture are crucial design choices impacting the performance of the overall system. While using harmonic priors simplifies geometry calculations and improves physical validity, careful consideration is required to balance the strength of this inductive bias with the model’s ability to generate diverse and novel conformations.
Chirality Handling#
Chirality, the handedness of molecules, is crucial for drug discovery as it significantly impacts biological activity. The paper addresses this by presenting a novel method for handling chirality in conformer generation. A post-hoc correction method, comparing generated conformer orientations against known chiral centers’ orientations using RDKit tags, is proposed. This simple yet effective approach allows for correcting chirality mismatches without significantly increasing computational cost. However, an alternative method, modifying the architecture to achieve SO(3) equivariance, is also explored for direct chirality incorporation, representing a potential avenue for future improvements. The choice between the post-hoc and the SO(3) equivariant approaches might depend on the computational resources and the desired accuracy in chirality predictions. The use of RDKit, a widely-used cheminformatics toolkit, enhances reproducibility and ease of implementation. The results demonstrate that even the simple post-hoc method is quite effective. Further investigation into the SO(3) approach might yield even more accurate and efficient chirality handling in the future.
Future Directions#
The paper’s ‘Future Directions’ section could explore several promising avenues. Improving the model’s scalability to handle larger molecules and more complex systems is crucial. This might involve exploring more efficient equivariant architectures or incorporating advanced sampling techniques. Addressing the limitations in recall—the model’s ability to generate diverse conformers—is another key area. Investigating alternative training methodologies or incorporating more sophisticated inductive biases could improve performance here. Incorporating dynamic interactions between molecules would enhance the model’s applicability to more realistic scenarios and could also boost the model’s overall accuracy. Finally, evaluating the model on diverse datasets is also vital to assess its generalization abilities and identify potential limitations. These directions would significantly advance the capabilities of molecular conformer generation models.
More visual insights#
More on figures
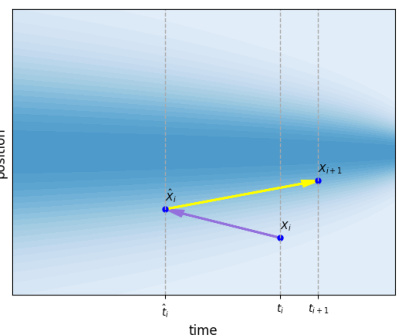
This figure illustrates the stochastic sampling process used during inference in the ET-Flow model. A noisy intermediate state (purple line) is created by adding noise to the position at time t (xt). The model then predicts the vector field (ût) using this noisy state instead of the original state (xt). The position is then updated using this predicted vector field to get the position at time t+1 (Xt+1), as shown by the yellow line. This process introduces stochasticity, improving sample diversity and accuracy. The figure showcases the steps in a time-position graph, where the shaded area represents the probability distribution.

This figure shows the recall and precision coverage results of ET-Flow, Torsional Diffusion, and MCF models on the GEOM-DRUGS dataset. The x-axis represents the threshold distance, and the y-axis represents the coverage (percentage). The plots show that ET-Flow outperforms the other methods, particularly at lower threshold distances, highlighting its ability to generate accurate conformers even with a tighter RMSD threshold. The figure includes separate plots for the mean and median coverage across different threshold values for both Recall and Precision.
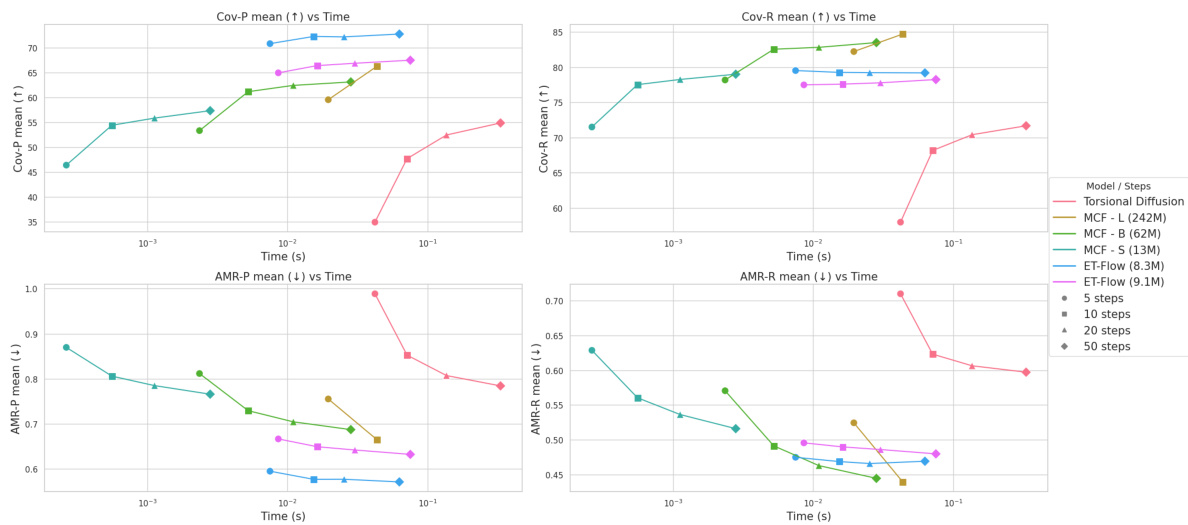
This figure presents the results of recall and precision coverage using various threshold distances on the GEOM-DRUGS dataset. It compares the performance of ET-Flow to Torsional Diffusion and MCF models. The graph shows ET-Flow significantly outperforming Torsional Diffusion across all threshold distances, and performing comparably or better to MCF, especially at lower thresholds indicating superior performance in generating accurate conformer predictions at lower RMSD thresholds.
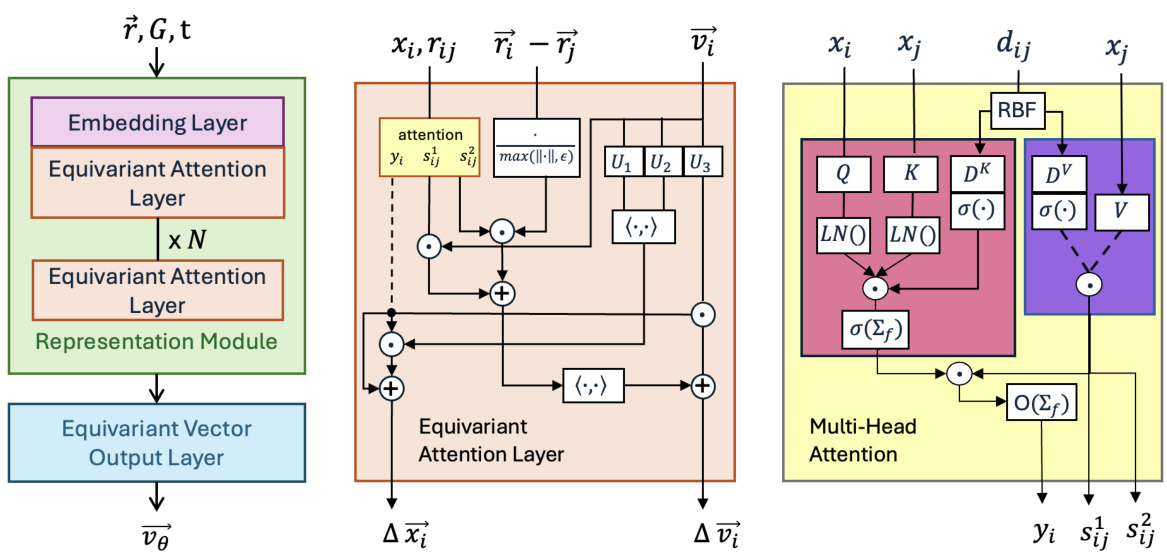
This figure shows the overall architecture of ET-Flow, which consists of two main parts: a representation module and an equivariant vector output module. The representation module uses a modified version of the TorchMD-NET architecture, incorporating equivariant attention layers to process molecular features. The output layer then uses gated equivariant blocks to produce the final conformer predictions. The figure also provides detailed diagrams of the equivariant attention layer and the multi-head attention block, highlighting the specific operations and components involved.
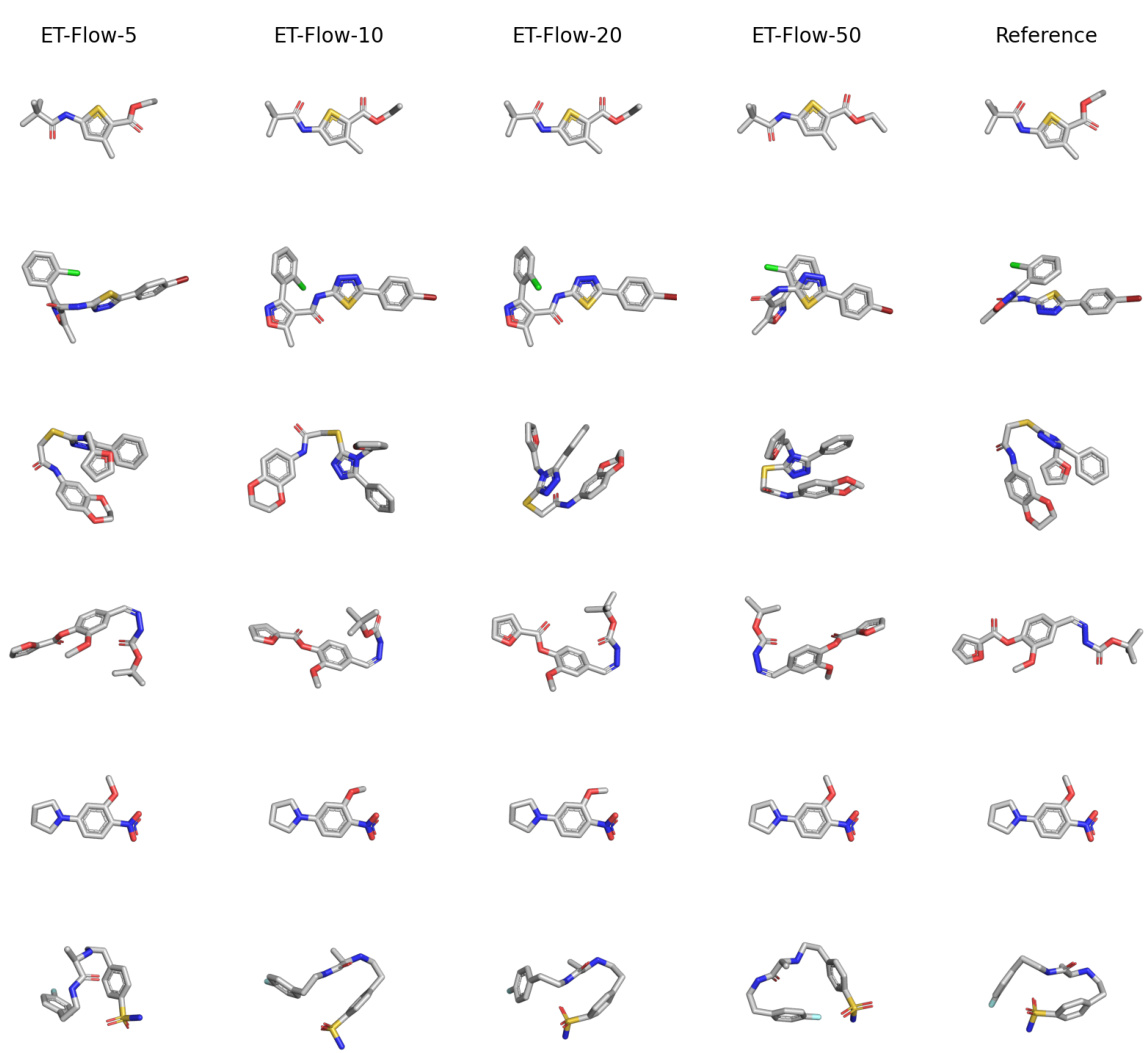
This figure visually demonstrates the effect of varying the number of sampling steps in the ET-Flow model on the generation of molecular conformers. It presents sets of conformers generated using 5, 10, 20, and 50 sampling steps, respectively. Each row compares the reference (ground truth) conformer to the conformers generated by ET-Flow with the varying numbers of steps. This allows for a visual assessment of how the model’s accuracy and diversity change with the number of sampling steps. Fewer steps mean less computation but possibly lower accuracy. The overall goal is to show that ET-Flow can produce quality samples even with fewer sampling steps.
More on tables
This table presents the results of molecular conformer generation experiments on the GEOM-QM9 dataset, using a distance threshold of 0.5 angstroms. It compares the performance of ET-Flow (with and without SO(3) architecture for chirality correction) against other state-of-the-art methods. The metrics used for comparison include coverage and average minimum root mean square deviation (AMR), both in terms of recall and precision.
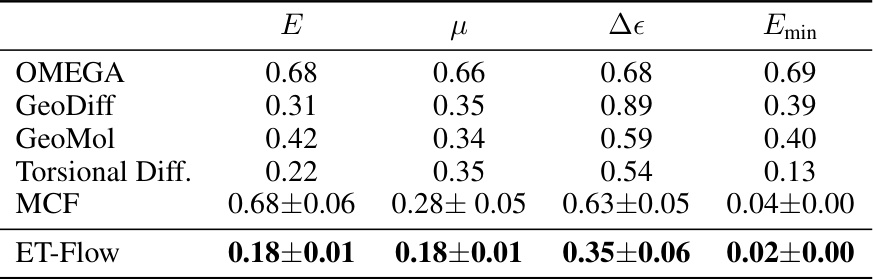
This table presents the median errors in predicting various molecular properties (energy, dipole moment, HOMO-LUMO gap, and minimum energy) for different conformer generation methods. The errors are calculated as the median difference between the predicted and true values for each property, comparing ensembles of generated and true conformers. Lower values indicate better prediction accuracy.
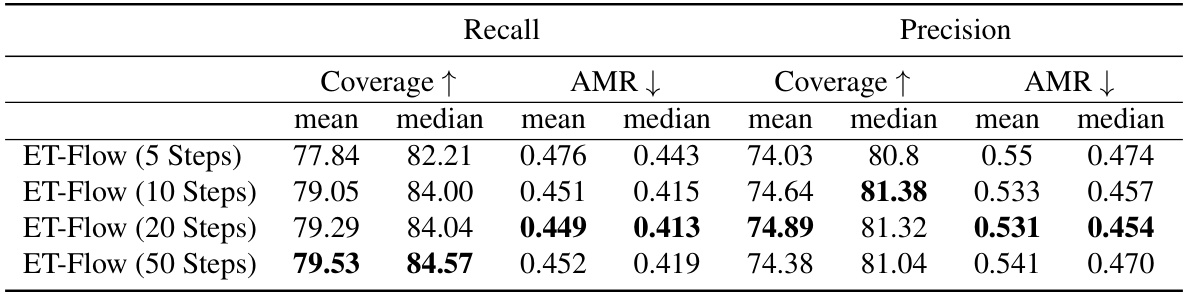
This table presents the results of molecular conformer generation experiments conducted using the GEOM-DRUGS dataset, where the root-mean-square deviation (RMSD) threshold (δ) was set to 0.75Å. The table compares the performance of ET-Flow (with and without stochastic sampling), ET-Flow with SO(3) architecture for chirality correction, and several other state-of-the-art methods. The metrics used for evaluation include Coverage (the percentage of ground truth conformers found), and Average Minimum RMSD (AMR, the average minimum distance between generated conformers and the ground truth conformers). Precision and recall values are also provided.

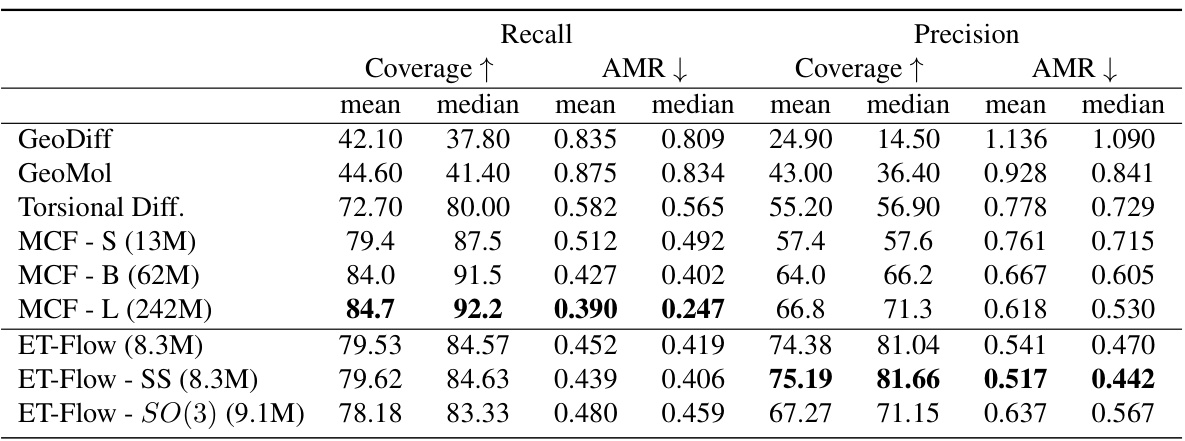
This table presents the results of molecular conformer generation experiments using the GEOM-DRUGS dataset. It compares the performance of ET-Flow (with and without stochastic sampling and SO(3) architecture for chirality correction) against other state-of-the-art methods. The metrics used for comparison include Coverage (the proportion of reference conformers covered by generated conformers), Average Minimum Root Mean Square Deviation (AMR, measuring the average distance between generated and reference conformers), and Recall and Precision values. The table highlights ET-Flow’s superior performance in terms of precision and accuracy, especially compared to models of similar size.

This table presents the results of molecular conformer generation experiments conducted on the GEOM-DRUGS dataset using three different versions of the ET-Flow model: the original ET-Flow, ET-Flow with stochastic sampling (ET-Flow-SS), and ET-Flow with SO(3) architecture for chirality correction (ET-Flow-SO(3)). The table compares the performance of these models to several baselines (GeoDiff, GeoMol, TorsionalDiff, and MCF with varying model sizes). Key metrics used for evaluation are coverage, average minimum RMSD (AMR), both in terms of median and mean values, and precision. The table shows that ET-Flow achieves competitive or state-of-the-art results in terms of precision and AMR.

This table presents the ablation study results on the GEOM-DRUGS dataset. It compares the performance of the ET-Flow model with several modifications against the original ET-Flow model. The modifications include using SO(3) architecture for chirality correction, removing the rotational alignment step, and using a Gaussian prior instead of the harmonic prior. The results are evaluated using Recall and Precision metrics, both of which include Coverage and Average Minimum RMSD (AMR). The table shows how these modifications affect the performance of the model in terms of Coverage and AMR for both Recall and Precision.
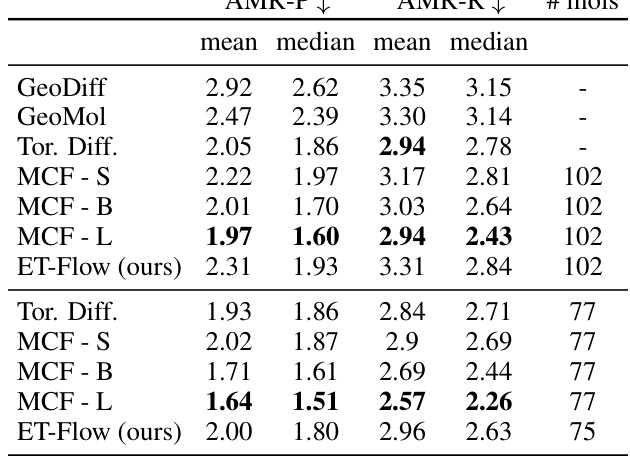
This table presents the results of molecular conformer generation experiments on the GEOM-QM9 dataset using a threshold distance of 0.5Å. It compares the performance of ET-Flow (with and without the SO(3) architecture for chirality correction) against other state-of-the-art methods. The metrics used for evaluation include Coverage and Average Minimum RMSD (AMR), both for Recall and Precision. Each method generated conformers over 50 time steps.
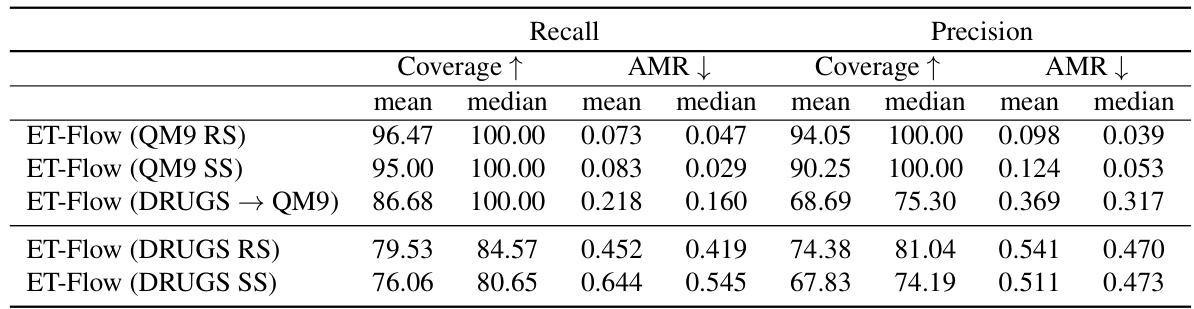
This table presents the results of out-of-distribution (OOD) experiments conducted to evaluate the generalization capability of the ET-Flow model. Two types of data splits are used: Random Split (RS) and Scaffold Split (SS). The results are compared against the baseline methods for different scenarios of training and testing on different datasets. This table shows the Recall and Precision with Coverage and Average Minimum Root Mean Square Deviation (AMR) for each setting.

This table presents the results of molecular conformer generation experiments conducted on the GEOM-DRUGS dataset. It compares the performance of ET-Flow (with and without stochastic sampling and SO(3) architecture for chirality correction) against several baseline methods. The metrics used for evaluation include Coverage (a measure of the diversity of generated conformers), and Average Minimum RMSD (AMR, a measure of the accuracy of generated conformers). The table highlights ET-Flow’s state-of-the-art performance in terms of precision, while maintaining competitiveness in recall with much larger models.
Full paper#