↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many existing causal inference estimators only address a subset of scenarios, like sequential back-door adjustment (SBD), lacking broad coverage and scalability. Recent attempts at more general estimators suffer from high computational costs due to summing over high-dimensional variables, limiting their applicability to real-world problems. This paper tackles these challenges head-on.
This work introduces Unified Covariate Adjustment (UCA), a novel framework that achieves broad coverage of causal estimands, extending beyond SBD and incorporating various sum-product functionals. UCA offers a scalable estimator that is computationally efficient and exhibits double robustness. The paper develops an estimator for UCA with computational efficiency and double robustness, providing finite sample guarantees and demonstrating its effectiveness through simulations. This addresses the limitations of prior approaches by providing a broadly applicable, efficient, and reliable method for causal effect estimation.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in causal inference because it introduces a novel, scalable framework (UCA) that significantly expands the range of causal estimands that can be efficiently estimated. This addresses a major limitation of existing methods which often lack scalability or are limited in their coverage. The unified approach, combined with a doubly robust estimator and finite sample guarantees, offers a powerful tool to analyze causal effects across various applications, from observational studies to intervention design. The improved scalability opens up new possibilities for tackling complex problems with high-dimensional data, advancing the field substantially.
Visual Insights#

This figure shows five different causal graphs representing various causal inference scenarios. Each graph illustrates a different adjustment method, including front-door, Verma, and standard fairness models. These graphs are used in the paper to illustrate the application of the Unified Covariate Adjustment (UCA) framework.

This table compares the coverage and scalability of existing causal effect estimators and the proposed Unified Covariate Adjustment (UCA) estimator. It shows that prior methods are limited in their coverage and often lack scalability, especially for more complex causal estimands beyond sequential back-door adjustments. The UCA method, however, addresses this limitation by achieving broader coverage and improved scalability.
In-depth insights#
Unified Adjustment#
A unified adjustment approach in causal inference aims to harmoniously integrate various covariate adjustment techniques under a single framework. This contrasts with traditional methods that often address only specific scenarios (e.g., back-door adjustment). A key benefit is enhanced coverage, enabling causal effect estimation in a wider range of situations that were previously intractable. Scalability is also a crucial aspect, as a unified approach must handle high-dimensional data efficiently. The development of a doubly robust estimator further enhances the robustness of inferences. This approach likely involves defining a general class of causal estimands and developing a corresponding estimation procedure that can adapt to diverse scenarios by systematically leveraging available covariate information. The effectiveness would be demonstrated through both theoretical analysis and empirical evaluations showing improvements in both coverage and computational efficiency. Unified adjustment represents a significant advancement, promoting greater flexibility, broader applicability, and stronger inference reliability in causal inference.
Scalable Estimator#
The heading ‘Scalable Estimator’ highlights a crucial aspect of the research: the computational efficiency of the proposed methodology. The authors likely address the challenge of applying causal inference methods to high-dimensional datasets, where traditional approaches become computationally intractable. The core idea is to develop an estimator that maintains accuracy while significantly reducing the computational burden. This is achieved by innovative techniques designed to scale polynomially with the number of variables and samples. Double robustness, often mentioned in conjunction with scalability, implies that the estimator remains reliable even if some model assumptions are slightly violated. The paper likely presents both theoretical justifications (e.g., error bounds) and empirical results (e.g., runtime comparisons) demonstrating the estimator’s scalability and robustness in various scenarios. The scalability is vital for the practical applicability of causal inference in large-scale, real-world problems.
Double Robustness#
Double robustness is a crucial property in causal inference, mitigating bias from the misspecification of either the outcome regression model or the propensity score model. If one model is correctly specified, the estimator remains consistent, unlike standard methods that require both to be accurate. This robustness is essential for reliable causal effect estimation given the inherent uncertainty in modeling complex relationships. The use of techniques like doubly robust estimators (e.g., targeted maximum likelihood estimation) leverages the information from both models, while incorporating clever weighting and adjustment mechanisms to reduce bias even when one model isn’t fully accurate. The robustness adds confidence to causal findings by protecting against potentially severe errors. The practical implications of double robustness are significant, allowing more reliable causal inferences from real-world data where model misspecification is common. Achieving it requires careful construction of the estimator, selection of appropriate models, and potentially techniques such as data splitting or cross-fitting to prevent overfitting.
UCA Expressiveness#
The UCA (Unified Covariate Adjustment) framework’s expressiveness lies in its ability to represent a wide array of causal estimands beyond the commonly used SBD (Sequential Back-Door) adjustment. Its flexibility stems from the incorporation of sum-product functionals, allowing it to handle scenarios where treatment variables play dual roles, as seen in the FD (Front-Door) adjustment and Tian’s adjustment. This broad coverage is demonstrated through examples encompassing various causal inference scenarios, including those involving nested counterfactuals and transportability, showcasing its applicability to a wider range of research questions. The ability to represent such diverse estimands in a unified manner streamlines the process of causal effect estimation, leading to increased efficiency and scalability in addressing complex causal relationships.
Future Directions#
Future research could explore extensions of UCA to handle more complex causal structures, such as those involving latent confounders or selection bias. Investigating the theoretical properties of UCA estimators under various data generating processes would strengthen its foundation. A significant area for improvement is developing more efficient algorithms for high-dimensional settings, addressing scalability limitations in real-world applications. Comparative studies against existing methods on diverse datasets, focusing on scenarios where UCA excels, are needed to demonstrate its practical advantages. Finally, developing user-friendly software tools would enhance accessibility and facilitate wider adoption of the UCA framework.
More visual insights#
More on figures

This figure compares the performance of the proposed DML-UCA estimator against existing methods for three different causal estimands: Front-Door, Verma’s equation and Jung’s equation. The top row shows running time as the dimension of summed variables increases, demonstrating DML-UCA’s scalability. The bottom row presents the average absolute error (AAE) as a function of sample size, highlighting DML-UCA’s robustness and faster convergence.

This figure shows five different causal graphs representing various scenarios in causal inference. (a) illustrates the front-door adjustment, where the treatment affects an intermediate variable which then influences the outcome. (b) demonstrates Verma’s equation, showcasing a more complex scenario with multiple intermediate variables. (c) depicts the ‘Napkin’ example, highlighting a situation where the causal effect cannot be expressed as a simple sum-product. (d) presents a standard fairness model, exhibiting the influence of a protected attribute (X) on the outcome (Y) through a mediator (W), involving confounding. Finally, (e) shows an additional graph from prior work.

This figure compares the performance of the proposed DML-UCA estimator against existing methods for various causal estimands (Front-Door, Verma, and Jung’s equation). The top row shows the running time of each estimator as the dimension of summed variables increases, demonstrating DML-UCA’s scalability. The bottom row displays the average absolute error (AAE) of each estimator as the sample size increases, highlighting DML-UCA’s robustness and faster convergence.
More on tables
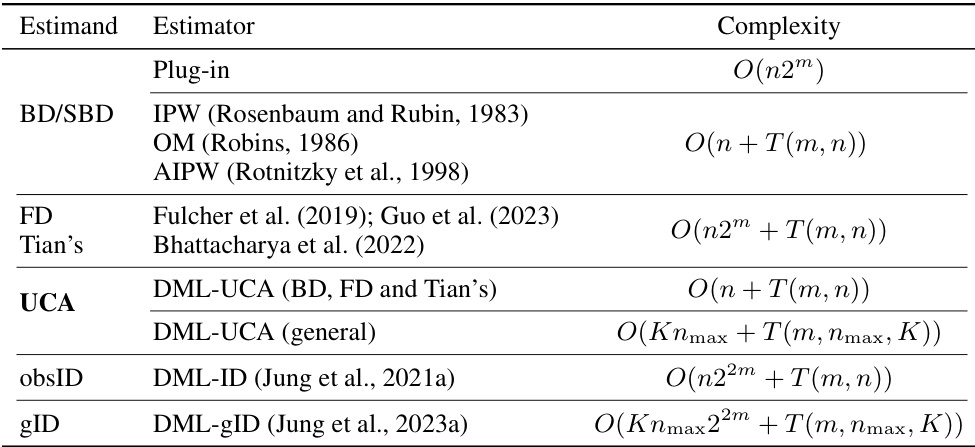
This table compares the computational complexities of various estimators for different causal estimands. It breaks down the complexity based on the number of samples (nmax), the number of variables (m), and the time it takes to learn nuisance parameters (T(m, nmax, K)). The table highlights the scalability of the proposed DML-UCA estimator, showing its superior efficiency compared to existing methods, particularly for high-dimensional settings.
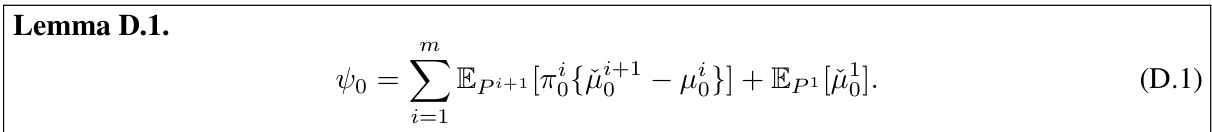
This table compares the computational complexities of various causal effect estimators across different functional classes (BD/SBD, FD, Tian’s, UCA, obsID, gID). It highlights the scalability (or lack thereof) of existing methods and introduces the DML-UCA estimator as a scalable and efficient alternative, especially for functionals beyond the standard BD/SBD.
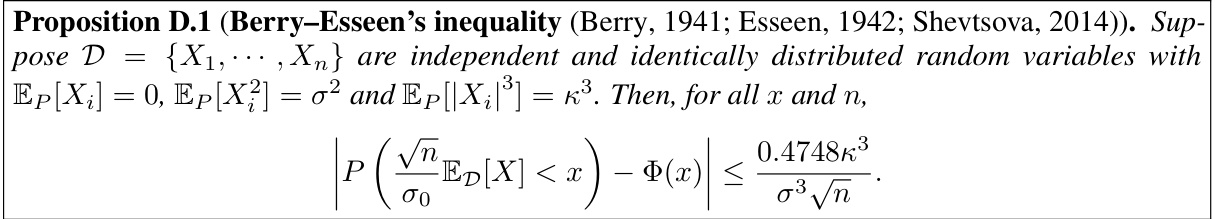
This table compares the time complexities of various estimators for different causal estimands (BD/SBD, FD, Tian’s, UCA, obsID, gID). It highlights the computational efficiency of the proposed DML-UCA estimator, particularly when compared to existing methods for estimands beyond simple back-door adjustments. The table also shows the impact of the number of samples, variables, and the complexity of learning nuisance parameters on the overall runtime.
Full paper#



















