↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Key Takeaways#
Why does it matter?#
This paper is important because it significantly improves the quality and efficiency of 3D surface reconstruction using Gaussian splatting. It addresses key limitations of existing methods, such as inconsistent normal predictions and slow processing speeds, opening new avenues for applications in areas like virtual reality, robotics, and computer graphics. The proposed techniques achieve state-of-the-art results on various benchmark datasets, demonstrating their effectiveness and practical value. Its faster training speed and real-time rendering capability make it particularly relevant for large-scale applications.
Visual Insights#

This figure illustrates the core idea of the View-Consistent Depth-Normal Regularizer (VCR-GauS) method. The left panel shows inconsistencies in pseudo-normals (estimated surface normals) predicted from a pre-trained monocular normal estimator across different views of a house. The middle panel displays a confidence map generated by the VCR-GauS method, highlighting areas where the pseudo-normals are more reliable. This confidence map is then used to weight the loss function, improving the accuracy of the final D-Normals. The right panel shows the high-quality 3D reconstruction and rendering achieved by VCR-GauS, demonstrating its superiority over existing methods.

This table presents a quantitative comparison of different methods for 3D surface reconstruction on the Tanks and Temples dataset. The methods are categorized into NeuS-based and Gaussian-based approaches. For each method, the table shows the F1-score (a measure of reconstruction accuracy), the average optimization time, and frames per second (FPS, a measure of efficiency). The results demonstrate that the proposed ‘Ours’ method significantly outperforms other Gaussian-based methods in terms of both accuracy and speed, while achieving comparable results to the best-performing NeuS-based methods.
In-depth insights#
View Consistent Normals#
Achieving view consistency in surface normal estimation is crucial for accurate 3D reconstruction. Inconsistent normals across multiple views lead to artifacts and inaccuracies in the final model. Methods addressing this challenge often involve sophisticated techniques to align or fuse normal maps from different viewpoints. This might include using depth information to constrain normal directions, employing robust estimation methods that handle outliers or noise, or designing a loss function that explicitly penalizes normal inconsistencies during training. A key consideration is how to weight the contributions of normals from each view, perhaps using confidence scores derived from the quality of individual normal estimates or from view-dependent factors like image quality or occlusion. Successfully creating view-consistent normals is a significant step toward building high-fidelity 3D models from multi-view data. The choice of methodology will depend on the specific application, the available data, and computational constraints. Ultimately, the goal is to generate a surface representation where the normals are not only accurate but also consistent across viewpoints, ensuring a coherent and realistic 3D model.
Depth-Normal Regularizer#
A Depth-Normal Regularizer, in the context of 3D surface reconstruction, is a method that jointly leverages depth and surface normal information to refine the geometry of a 3D model. It addresses limitations of using only normal information, which often fails to accurately capture the positional details of the surface. By combining depth and normal information, the regularizer can provide more comprehensive constraints to optimize the 3D model’s parameters, such as the position and orientation of individual surface elements (e.g., 3D Gaussians in Gaussian Splatting). This approach results in more accurate and detailed surface reconstructions compared to methods solely relying on normal estimation. A key advantage is the ability to mitigate inconsistencies among normals predicted from different views, improving overall surface quality. A well-designed Depth-Normal Regularizer may use a confidence term to weigh the influence of normal estimates based on their reliability, further enhancing the robustness and accuracy of the reconstruction process. A view-consistent approach is particularly beneficial in multi-view stereo settings.
Gaussian Surface Recon#
Gaussian surface reconstruction, a core concept in 3D modeling and computer vision, aims to create a realistic surface representation of an object from point cloud data or other multi-view information. This process often leverages Gaussian functions due to their smooth, flexible nature, which simplifies computations. The key challenge lies in handling noise and inconsistencies, particularly when dealing with multiple viewpoints. Methods might utilize techniques like normal supervision or depth integration to guide the fitting process, while sophisticated regularization techniques can address the complexities arising from the statistical distributions of Gaussian components. Optimizing for accuracy and speed is crucial, especially for large-scale or real-time applications, potentially involving efficient algorithms and hardware acceleration. Therefore, a robust Gaussian surface reconstruction method must effectively balance computational cost, accuracy, and the ability to handle noisy input data. The ultimate goal is to generate a high-fidelity representation suitable for tasks such as rendering, 3D printing, or other downstream applications.
Densification & Splitting#
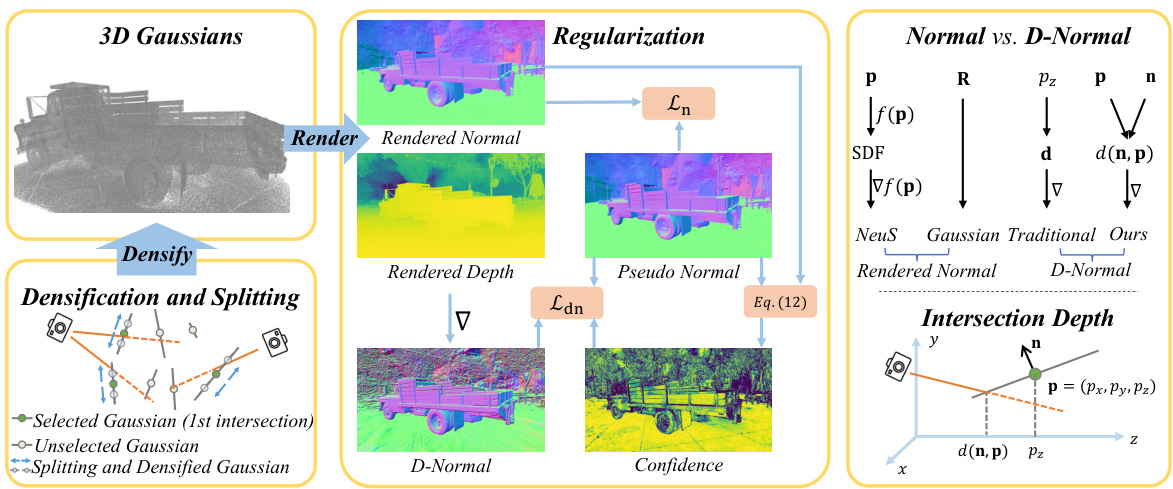
The paper introduces a novel densification and splitting strategy to enhance 3D Gaussian surface reconstruction. The core idea is to address depth errors and surface irregularities arising from the use of large Gaussians. Large Gaussians, while computationally efficient, can lead to significant depth errors from small normal inconsistencies. The proposed strategy strategically splits large Gaussians along their major principle axes into smaller ones, improving accuracy. This process is carefully managed to avoid introducing new artifacts or inconsistencies. The selection of which Gaussians to split and how to split them is also detailed, demonstrating a thoughtful approach to this problem. The method is shown to improve accuracy and maintains competitive appearance quality, indicating the effectiveness of this novel strategy in refining the Gaussian surface representation and delivering improved reconstruction results.
Limitations & Future#
A critical analysis of the ‘Limitations & Future’ section of a research paper would delve into the acknowledged shortcomings of the presented work. Specific limitations might include issues with the dataset size or quality, assumptions made during model development, or computational constraints affecting scalability. The discussion should also address the generalizability of findings—do the results hold across diverse datasets or settings? The paper should honestly assess the methodological limitations, perhaps addressing issues with the evaluation metrics used or limitations imposed by the experimental design. A strong ‘Future’ component outlines directions for future research that directly address these limitations. This could involve improving the model’s robustness, exploring new datasets, refining the methodology, or extending the work to new applications. Specific, achievable goals for future work should be proposed, strengthening the paper’s impact and showing a clear path forward.
More visual insights#
More on figures

This figure illustrates the difference between rendered normal supervision and the proposed D-Normal regularizer in Gaussian splatting. It shows how rendered normal supervision (Ln) only moves Gaussians closer or further from a ray, failing to effectively pull them towards the surface. In contrast, the D-Normal regularizer (Ldn) uses depth information to directly move Gaussians towards or away from the ground truth surface, improving surface reconstruction accuracy.
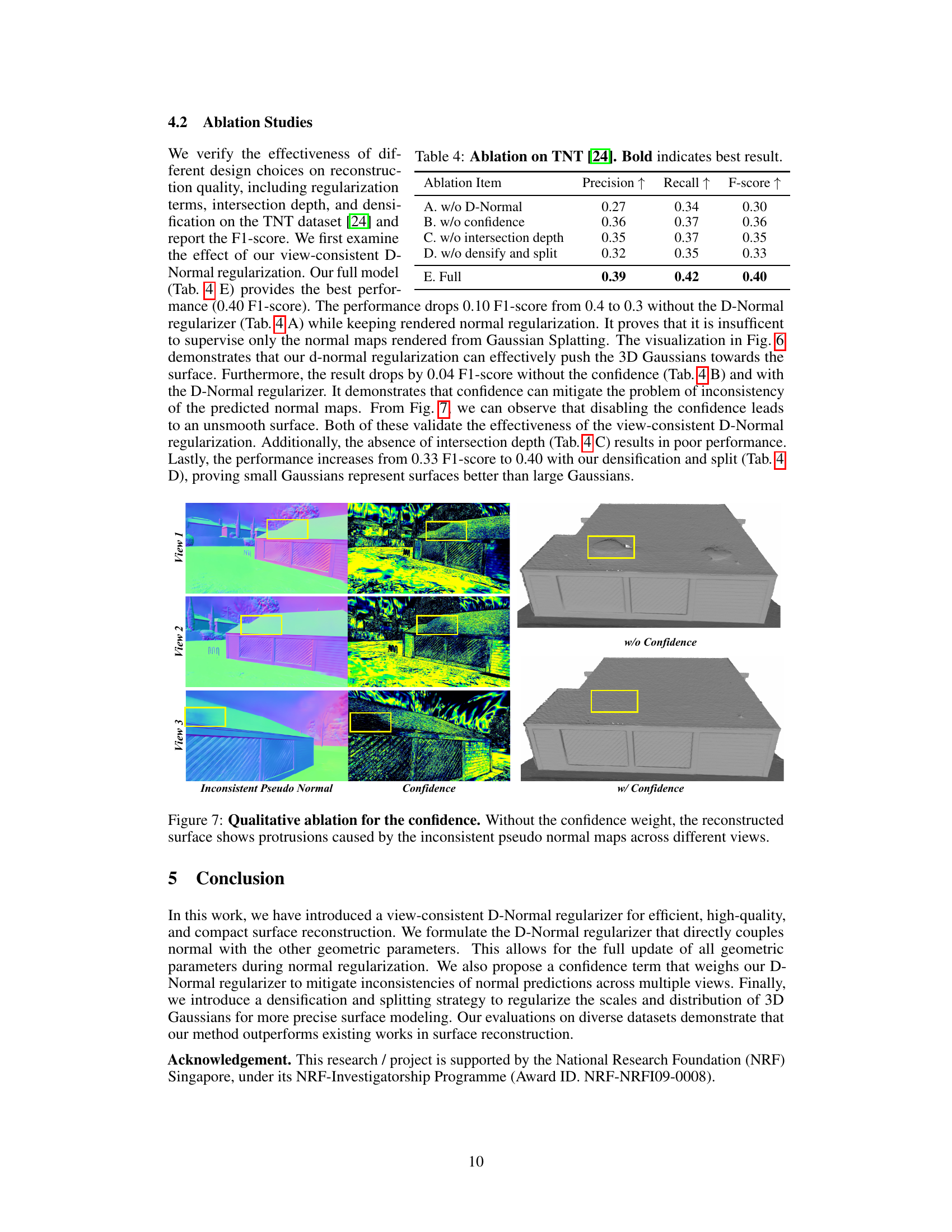
This figure provides a visual overview of the VCR-GauS method, highlighting the key steps involved in surface reconstruction. It shows how the method uses 3D Gaussians, regularizes them using a depth-normal approach incorporating confidence from a pretrained model, and refines the surface using densification and splitting strategies. The image is divided into four key parts to detail each part of the pipeline, from 3D Gaussian generation, to regularization, comparing normal and D-Normal methods and details of depth intersection.
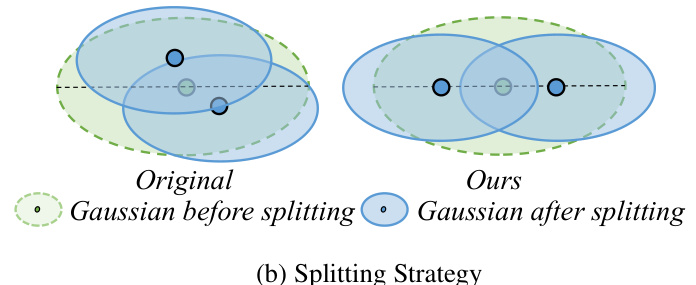
This figure illustrates the reasoning behind the densification and splitting strategies used in the proposed method. Panel (a) shows that depth errors caused by small normal errors are significantly larger for large Gaussians than for small ones. This motivates densifying large Gaussians into smaller ones to reduce depth errors. Panel (b) compares the original Gaussian splitting method with the proposed method, showing that the proposed method avoids clustering of split Gaussians, which can lead to surface protrusions and inaccuracies.
This figure illustrates the reasoning behind the densification and splitting strategies used in the proposed method. Part (a) shows how a small error in normal estimation leads to larger depth errors for large Gaussians, motivating the splitting of large Gaussians into smaller ones. Part (b) compares the original splitting strategy with the proposed one, highlighting how the new method aims to mitigate Gaussian clustering and surface protrusions.

This figure compares the 3D surface reconstruction results of four different methods (VCR-GauS, SuGar, 2DGS, NeuS) on three scenes from the Tanks and Temples dataset. The top row shows the reconstructions generated by the proposed VCR-GauS method. The subsequent rows display the results from SuGar, 2DGS, and NeuS respectively. The bottom row presents the ground truth point clouds for comparison. The visual comparison highlights that VCR-GauS produces more complete and detailed reconstructions with smoother surfaces, particularly in planar regions, compared to other methods.

This figure shows an ablation study comparing surface reconstruction results with and without a confidence term in the D-Normal regularizer. The left image displays the result without the confidence term, illustrating surface protrusions caused by inconsistent pseudo normal maps across multiple views. The right image shows the reconstruction with the confidence term, demonstrating improved smoothness and accuracy by mitigating the effects of inconsistent normals.

This figure illustrates the view-consistent D-Normal regularizer proposed in the paper. It shows how inconsistent pseudo-normals (predicted from a pre-trained model) are across different views. The authors’ method addresses this by calculating a confidence map that weights the loss during the optimization process of their D-Normals. This leads to improved surface reconstruction and rendering quality compared to previous methods.

This figure shows a comparison of 3D reconstruction results with and without semantic surface trimming. The left image shows the reconstruction without trimming, resulting in the inclusion of unwanted background elements such as the sky. The right image demonstrates the result with semantic trimming, effectively removing the sky and other background elements to focus solely on the target object.

This figure provides a visual overview of the VCR-GauS method, highlighting the key steps involved in densification, splitting, normal supervision, and depth calculation. It shows how the algorithm refines the 3D Gaussian representation of a scene by selectively splitting large Gaussians, incorporating pseudo-normals from a pretrained model weighted by a confidence term, and using intersection depth instead of Gaussian centers for more accurate depth estimation. The top right shows different normal calculation methods, comparing traditional and D-Normal methods, while the bottom right details the proposed intersection depth calculation.

This figure presents a qualitative comparison of 3D surface reconstruction results on the Replica dataset. It shows results from the proposed method (Ours), SuGar, 2DGS, and the ground truth (GT). Each row compares a specific scene from different viewpoints, allowing for a visual assessment of the accuracy and completeness of the 3D models generated by each method. The comparison highlights the strengths and weaknesses of each approach in terms of detail preservation, surface smoothness, and overall accuracy in reconstructing the scene from multiple viewpoints.

This figure shows the effectiveness of the proposed view-consistent D-Normal regularizer. The left side illustrates the inconsistency of pseudo-normals predicted by a pre-trained monocular normal estimator across different views. The middle shows a confidence map generated by the method, indicating the reliability of these pseudo-normals. This confidence map is then used to weight the loss function for the D-Normals, leading to improved consistency. The right displays the high-quality reconstructed scene geometry and texture achieved by the method, showcasing its state-of-the-art performance.

This figure showcases the effectiveness of the proposed View-Consistent Depth-Normal Regularizer in addressing inconsistencies in pseudo-normal predictions from different viewpoints. The left side shows inconsistencies in pseudo-normals from a pre-trained model. The middle shows a confidence map generated by the method, which indicates the confidence levels of the pseudo normals. This confidence map is then used to weigh the loss function applied to the D-Normals in the proposed method. The right demonstrates the improved quality of reconstructed scene geometry and texture using the proposed approach, highlighting its state-of-the-art performance.

This figure illustrates the core concept of the proposed View Consistent Depth-Normal Regularizer (VCR-GauS). The left panel shows inconsistencies in pseudo-normals predicted by a pre-trained monocular normal estimator across different viewpoints. The middle panel demonstrates a confidence map generated by the method, which assesses the reliability of these pseudo-normals. Finally, the right panel presents the improved 3D scene geometry and texture achieved by using the confidence map to weigh the loss applied to the D-Normals (Depth-Normals), resulting in state-of-the-art surface reconstruction and rendering quality.
More on tables
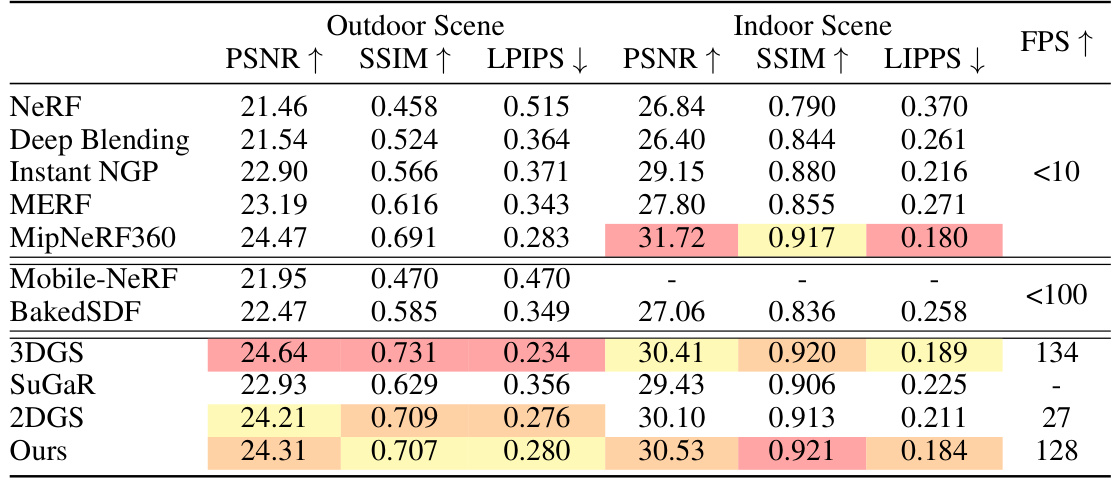
This table presents a quantitative comparison of different methods for 3D surface reconstruction on the Tanks and Temples dataset. The metrics used are F1-score (a measure of accuracy), average optimization time, and frames per second (FPS, a measure of efficiency). The results show that the proposed ‘Ours’ method significantly outperforms other Gaussian-based methods in terms of both accuracy and speed, and achieves comparable performance to neural implicit methods while being substantially faster.

This table presents a quantitative comparison of different methods for 3D surface reconstruction on the Replica dataset [43]. The methods are categorized into implicit and explicit approaches. The table shows the F1-score achieved by each method and the corresponding computational time taken for the reconstruction. The F1-score is a measure of the accuracy of the surface reconstruction, while the time indicates the efficiency of the method. The best-performing method for each category is highlighted in bold.
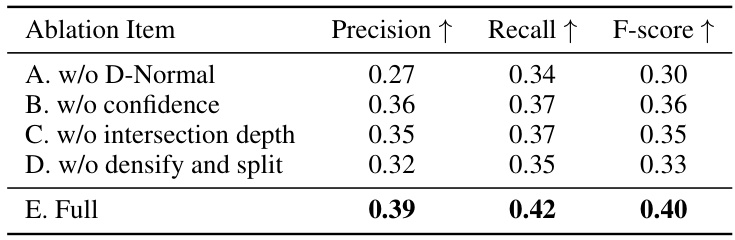
This table presents the ablation study results on the Tanks and Temples (TNT) dataset [24]. It shows the impact of different components of the proposed VCR-GauS method on the reconstruction performance, measured by precision, recall, and F1-score. The ablation study removes one component at a time to isolate its contribution and assess its impact. The ‘Full’ row represents the performance of the complete VCR-GauS model, serving as a baseline. The results demonstrate the importance of each component, with the full model achieving the best overall performance.

This table shows the ablation study results on the Tanks and Temples dataset. It compares the performance of the proposed method with several variations, such as removing the semantic trimming, scale regularization, and different ways of handling the scaling factor of 3D Gaussians. The results are presented in terms of precision, recall, and F-score, which are common metrics for evaluating the performance of surface reconstruction methods.
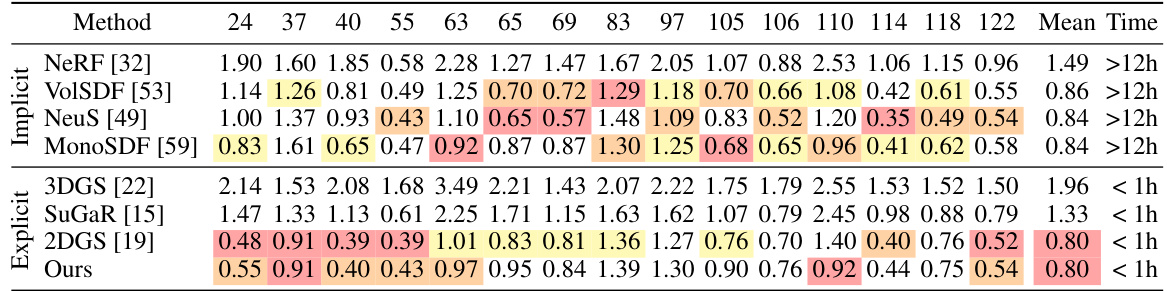
This table presents a quantitative comparison of different methods for 3D surface reconstruction on the Tanks and Temples dataset. The metrics used are F1-score (a measure of reconstruction accuracy), average optimization time, and frames per second (FPS, a measure of computational efficiency). The results show that the proposed ‘Ours’ method significantly outperforms other Gaussian-based methods (3DGS, 2DGS, SuGaR) in terms of F1-score and computational speed, while achieving comparable results to neural implicit methods (NeuS, MonoSDF, Geo-NeuS).
Full paper#