↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current Implicit Neural Representations (INRs) for 3D shape reconstruction struggle with pose variations and lack generalization across datasets. They often treat distinct local regions as independent geometry elements, ignoring the fact that similar intrinsic geometries repeatedly appear in different poses. This leads to issues with orientation robustness and cross-dataset performance.
The paper introduces a Patch-level Equivariant Implicit Function (PEIF) that tackles these issues. PEIF utilizes a pose-normalized query/patch representation and incorporates an intrinsic patch geometry representation to learn pose-invariant features. This design enables patch-wise equivariance, resulting in a method that accurately reconstructs surfaces regardless of pose and demonstrates improved cross-dataset generalization and superior robustness to rotations.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel approach to 3D surface reconstruction that is robust to pose variations and generalizes well across different datasets. This addresses a key limitation of existing methods, opening up new avenues for applications in robotics, computer vision, and other fields that rely on accurate 3D models. The use of patch-level equivariance is a significant contribution that can influence future research in deep learning and geometric modeling. Furthermore, the proposed model’s state-of-the-art performance on various benchmarks underscores its practical significance.
Visual Insights#
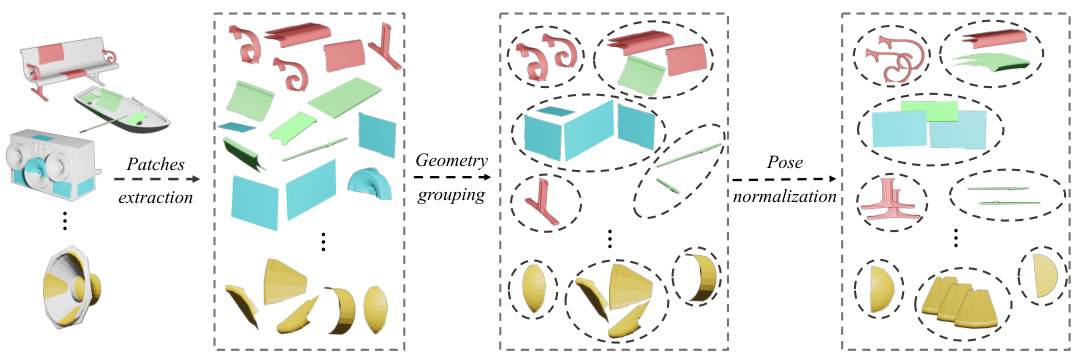
This figure illustrates the core idea behind the paper’s approach. It shows that many 3D shapes contain repeated local geometric structures, even if their poses (orientations and positions) differ significantly. By removing the effects of pose, the algorithm can learn these recurring patterns and thus achieve more robust and efficient 3D shape reconstruction.
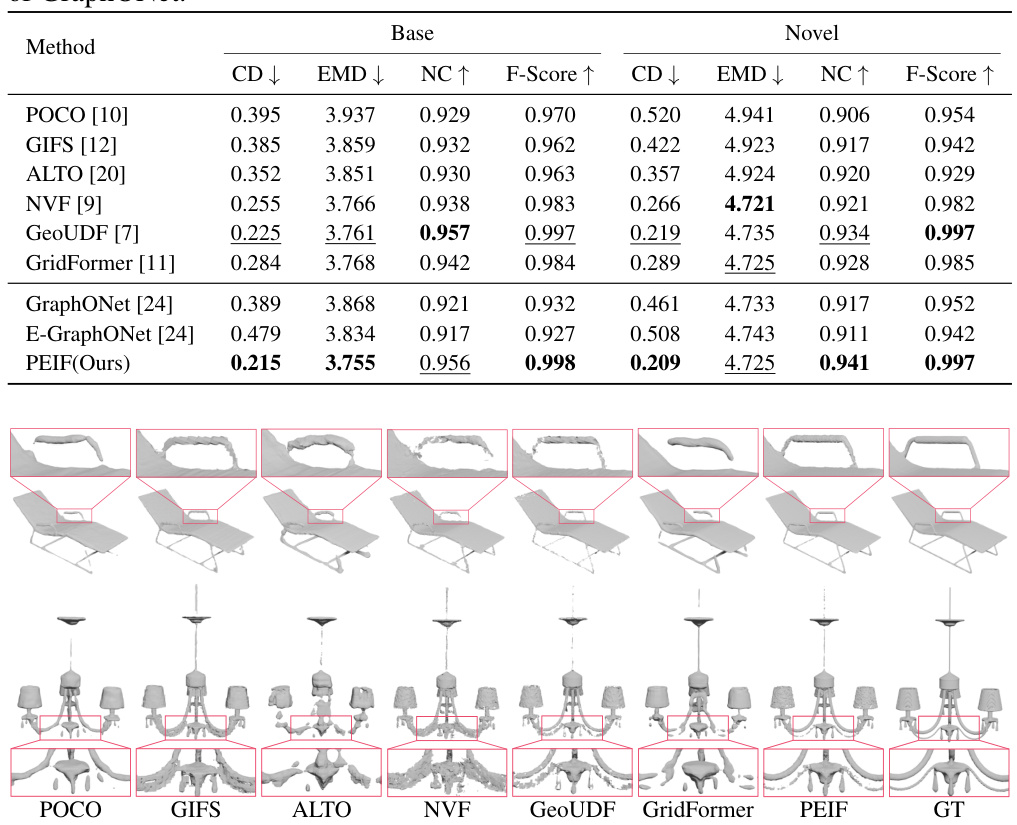
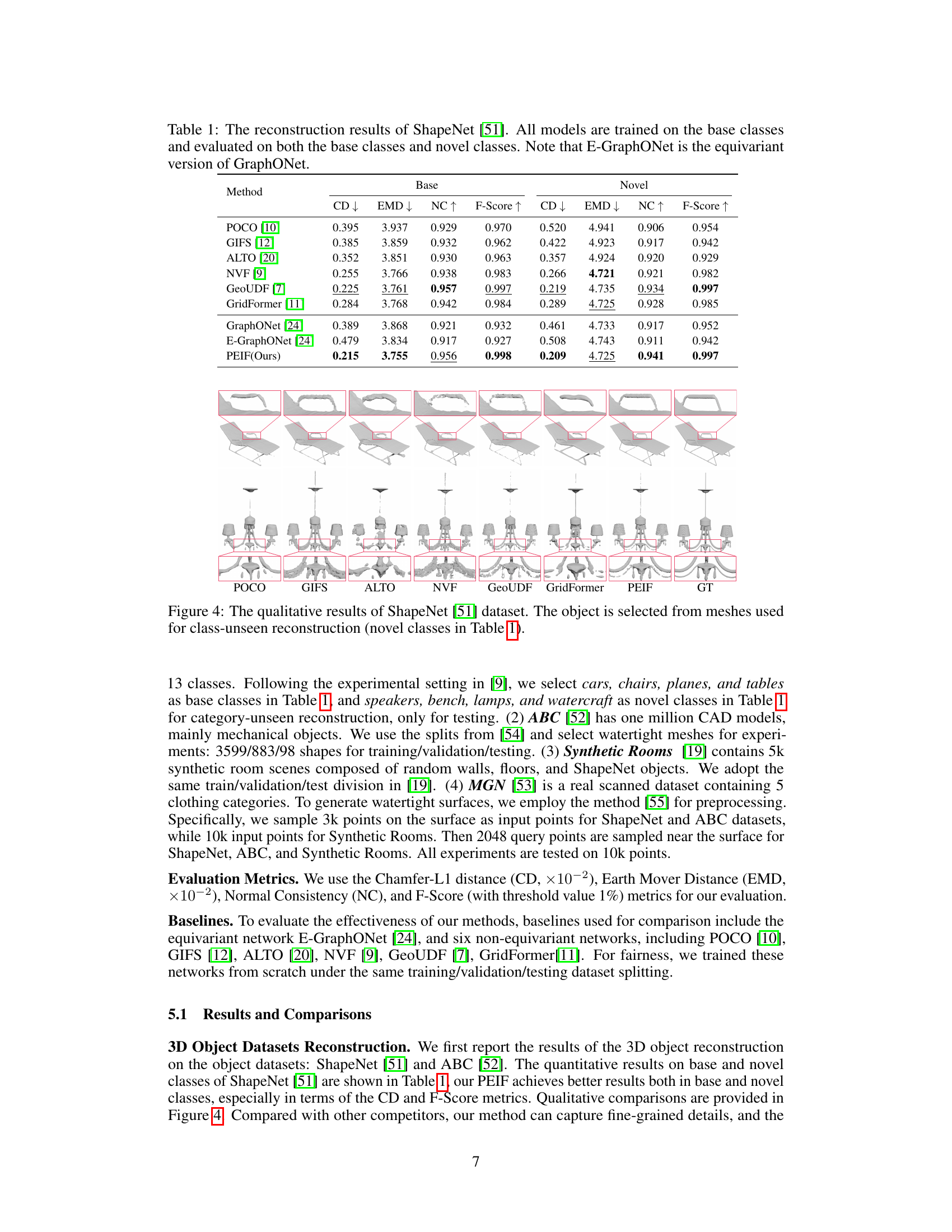
This table presents the quantitative results of 3D shape reconstruction on the ShapeNet dataset. It compares the performance of the proposed PEIF method against several other state-of-the-art methods (POCO, GIFS, ALTO, NVF, GeoUDF, GridFormer, GraphONet, and E-GraphONet). The comparison is done for both base classes (classes used during training) and novel classes (classes unseen during training) to evaluate generalization capabilities. Metrics used include Chamfer distance (CD), Earth Mover’s distance (EMD), Normal Consistency (NC), and F-Score, all of which are commonly used for evaluating 3D shape reconstruction quality.
In-depth insights#
3D Patch Equivariance#
3D patch equivariance is a crucial concept in building robust and generalizable 3D deep learning models. It leverages the inherent geometrical structure of local 3D patches, which often repeat across various poses on a 3D shape. By focusing on the intrinsic geometry of these patches, rather than their absolute orientation, 3D patch equivariance makes models more resilient to arbitrary rotations and translations. This is achieved by normalizing the patches to a canonical pose before feeding them into the network, essentially removing redundant positional information. Consequently, the network learns to extract pose-invariant features, improving generalization across diverse datasets and preventing distortions caused by variations in object pose. Multi-head memory banks can further enhance this approach by capturing the common patterns of intrinsic patch geometries, ultimately leading to more accurate and efficient 3D shape reconstruction.
Pose-Invariant Feat.#
The concept of “Pose-Invariant Feat.” in 3D object analysis addresses the challenge of extracting features that are robust to variations in object orientation. Traditional methods often struggle because changes in pose significantly alter the raw feature representations. Pose invariance is crucial because it allows algorithms to recognize the same object regardless of its position and rotation. This is achieved through techniques like canonicalization (aligning objects to a standard orientation) or learning representations that explicitly disregard positional and rotational information. Methods focusing on intrinsic geometric properties (e.g., distances between points, curvature) or using SE(3)-equivariant neural networks offer promising routes to pose invariance. Successfully creating pose-invariant features significantly improves the accuracy and generalization of 3D shape recognition, retrieval, and reconstruction systems, making them less susceptible to the effects of noise or viewpoint variation. A key aspect is defining what constitutes a meaningful “pose” for a given application; the definition might encompass full six-degree-of-freedom transformations or focus on subsets, like rotations around a specific axis. The complexity of the chosen pose normalization techniques will influence computational cost and accuracy. Therefore, a well-defined understanding and the use of effective techniques to achieve pose invariance are critical to obtaining robust and reliable performance in 3D computer vision tasks.
Multi-head Memory#
The concept of “Multi-head Memory” in the context of a deep learning model for 3D reconstruction suggests a powerful mechanism to enhance the model’s ability to learn and generalize from complex 3D shape data. It likely involves a neural network architecture where multiple independent memory banks are used to store and retrieve information related to different geometric features or patterns within 3D shapes. Each “head” could specialize in a specific type of geometric feature, allowing the model to efficiently capture a rich representation of the 3D shape’s intrinsic geometry. This approach addresses the challenge of variations in pose and viewpoint in 3D data by focusing on the underlying geometric structure. The use of multiple heads provides an advantage over single-head memory because it allows the model to learn a more comprehensive and nuanced representation of the shapes. It also enables parallel processing, potentially leading to more efficient training and inference. This approach is likely combined with some mechanism for querying the memory banks, possibly based on a representation of the input geometry, and for aggregating the information from different memory banks. The effectiveness of multi-head memory hinges on the design of the memory banks themselves, their query mechanisms, and how the retrieved information is used to guide the reconstruction process. The model’s performance will likely be further improved by incorporating learned relationships between features stored in different memory banks.
Rotation Robustness#
Rotation robustness in 3D deep learning models is crucial for real-world applications, as objects are rarely observed from a single viewpoint. This research paper likely investigates the performance of 3D shape reconstruction or related tasks under various rotations. A key challenge is that methods which don’t inherently consider rotational invariance may struggle to generalize across different viewpoints. The paper may introduce techniques like equivariant neural networks, which naturally embed rotational invariance into their architecture, or other approaches such as data augmentation, which artificially introduces rotations to the training set. Success in rotation robustness would be measured by metrics such as Chamfer distance or other quantitative evaluations showing consistent accuracy despite arbitrary rotations of the input 3D data. Generalization to unseen rotations or datasets would also be a significant indicator of robustness and a key focus of the evaluation.
Future Extensions#
Future research directions stemming from this work could explore several promising avenues. Extending the patch-level equivariant implicit function to handle more complex scenarios such as scenes with highly varying densities or shapes with intricate details would be valuable. Furthermore, investigating the use of more sophisticated pose normalization techniques than PCA, possibly leveraging learned representations or other geometric features, could enhance robustness and accuracy. Another avenue is integrating PEIF with other 3D shape processing methods, creating a hybrid approach that combines the strengths of different techniques. This could involve incorporating the advantages of explicit representations for detailed features, or leveraging the power of point cloud segmentation for more efficient shape reconstruction. Finally, exploring the application of PEIF to other domains where SE(3) equivariance is crucial, like molecular dynamics or robotics, could unveil novel and impactful applications.
More visual insights#
More on figures
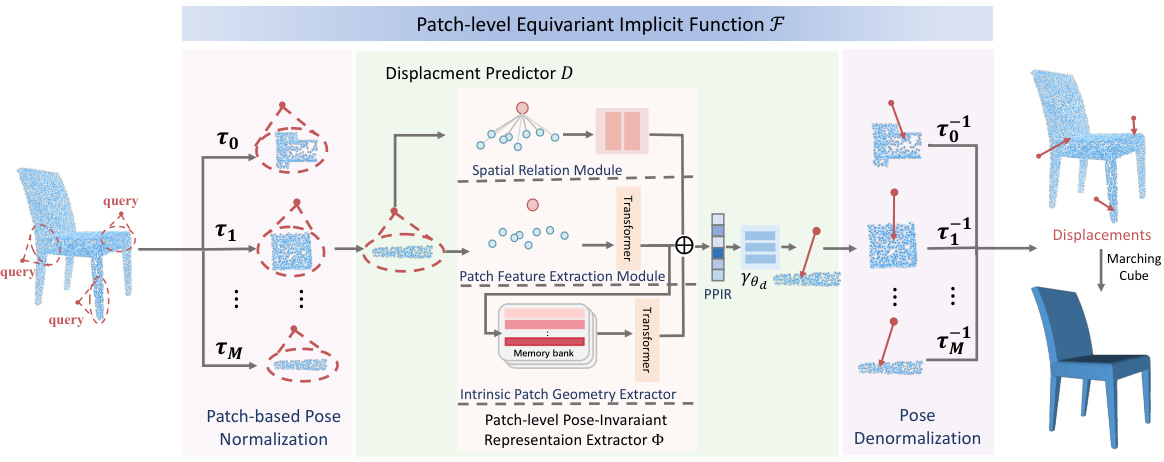
This figure illustrates the architecture of the proposed Patch-level Equivariant Implicit Function (PEIF). It shows how the model takes query points as input, selects local patches using KNN, normalizes these patches and query points using pose transformations (τ), and then uses a displacement predictor (D) to estimate the displacement vectors. The model is designed to be equivariant under SE(3) transformations. Finally, a marching cubes algorithm generates the 3D mesh.
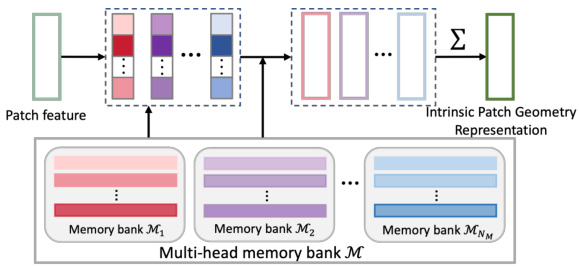
This figure illustrates the Intrinsic Patch Geometry Extractor (IPGE) module. The input is a patch feature. This feature is then enhanced by querying and aggregating information from a multi-head memory bank M = {Mᵢ}. Each Mᵢ is a memory bank with multiple memory items. The query is performed using learnable weights, creating a weighted aggregation that enhances the patch feature’s representation of intrinsic 3D patch geometry. The output is the enhanced feature, representing the intrinsic patch geometry representation.

This figure shows a visual comparison of cross-domain evaluation results on the MGN dataset. The model was pre-trained on the Synthetic Rooms dataset. It highlights the ability of the proposed PEIF model to generalize to unseen real-world data, while other methods struggle with incomplete or rough surface reconstructions. Red boxes indicate regions of interest where the model performance differences are most notable.

This figure illustrates the core idea of the paper. It shows that many local 3D patches on different 3D shapes share similar geometric characteristics, even though their orientations (poses) differ. The key insight is that by removing the pose variations, these repeated local patterns can be identified and efficiently represented. This leads to the concept of a patch-level pose-invariant representation, which is a crucial part of the proposed PEIF (Patch-level Equivariant Implicit Function).

This figure illustrates the core idea of the paper. Local 3D patches from various 3D shapes are shown. While the patches have different poses (orientations and positions in 3D space), their intrinsic geometric structure is very similar. The paper leverages this observation to develop a pose-invariant representation for the patches, which improves the efficiency and robustness of 3D surface reconstruction.

This figure shows a qualitative comparison of the 3D object reconstruction results on the ShapeNet dataset. The models were tested on novel classes (classes not seen during training), and the results are presented for several different methods: POCO, GIFS, ALTO, NVF, GeoUDF, GridFormer, and the authors’ proposed PEIF method. Ground truth (GT) models are also included. The image highlights the ability of PEIF to capture finer details and achieve more robust and complete reconstructions, particularly in comparison to other approaches.

This figure showcases the qualitative results of the proposed method, PEIF, on the ShapeNet dataset. It specifically focuses on class-unseen reconstruction, meaning that the model is tested on shapes that it hasn’t seen during training. The top row displays the ground truth (GT) meshes, and the bottom row shows the reconstructions generated by the PEIF model. The figure aims to visually demonstrate the PEIF’s ability to reconstruct novel objects with high fidelity and detail.

This figure shows a comparison of the ground truth (GT) 3D reconstruction of a synthetic room scene with the reconstructions produced by several different methods: POCO, GIFS, ALTO, NVF, GeoUDF, GridFormer, and PEIF (the proposed method). The red boxes highlight areas where some methods fail to reconstruct parts of the scene accurately or completely.

This figure shows a comparison of cross-domain evaluation results on the real scanned MGN dataset. The model was pre-trained on the Synthetic Rooms dataset. The top row displays the ground truth (GT) 3D models of clothing items. Subsequent rows show the reconstruction results from different methods: GeoUDF, NVF, GridFormer, and the proposed PEIF. Each method’s reconstruction is presented alongside extracted patches, highlighting the model’s ability (or lack thereof) to generalize to unseen data. Red boxes represent correctly reconstructed patches while purple boxes indicate poorly reconstructed areas. The figure illustrates that the PEIF method achieves better generalization performance to real-world scans compared to other methods.
More on tables
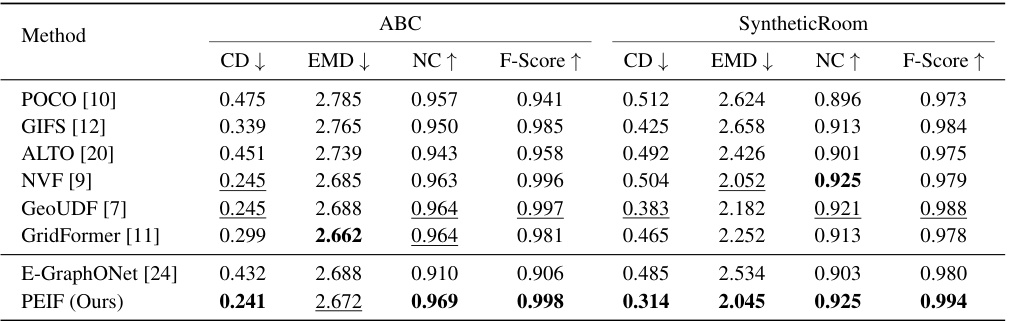
This table presents a quantitative comparison of different 3D reconstruction methods on two datasets: ABC and Synthetic Rooms. For each method, the table shows Chamfer distance (CD), Earth Mover’s Distance (EMD), Normal Consistency (NC), and F-Score metrics, lower is better for CD and EMD, higher is better for NC and F-Score. The results allow for a direct comparison of the performance of the proposed PEIF method against existing state-of-the-art techniques across different datasets.
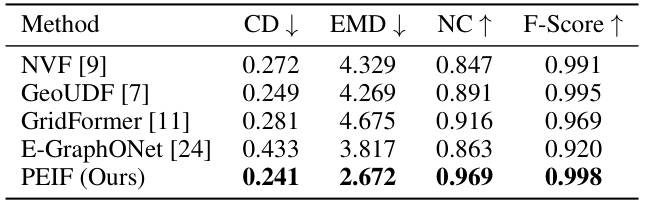
This table presents the results of a cross-domain evaluation experiment conducted on the MGN dataset. The model was pre-trained on the Synthetic Rooms dataset and then evaluated on the MGN dataset. The table shows that several methods experienced a performance decrease due to the domain gap between synthetic and real-world data. However, PEIF (the authors’ method) maintained high performance, showing good generalization.
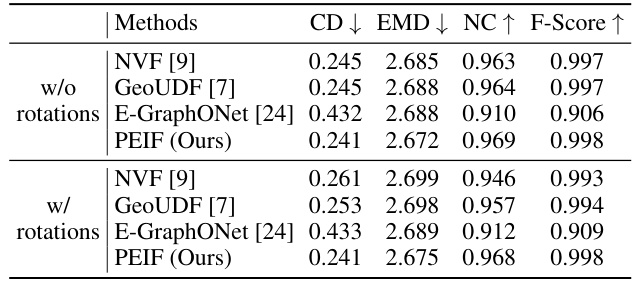
This table compares the robustness of four different methods (NVF, GeoUDF, E-GraphONet, and PEIF) to arbitrary rotations. The methods are trained with canonical poses and then tested on the ABC dataset with and without arbitrary rotations. The table shows the Chamfer distance (CD), Earth Mover’s Distance (EMD), Normal Consistency (NC), and F-score for each method under both conditions (with and without rotations). The results demonstrate the invariance or equivariance of the methods to rotations and highlight the performance of PEIF under rotated input.

This table presents the results of ablation studies conducted on the ABC dataset to analyze the impact of different components of the proposed PEIF model. It shows the effect of removing pose normalization, varying the number of memory banks (NM), and changing the number of nearest neighbors (K) used for KNN. The results are evaluated using CD, EMD, NC, and F-Score metrics, demonstrating the contribution of each component to the overall performance.
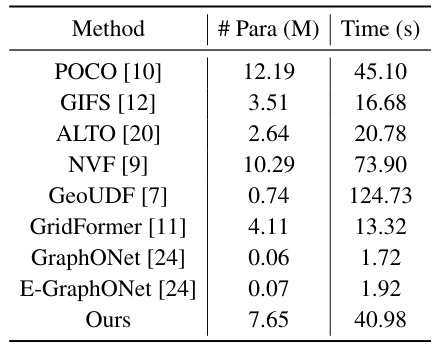
This table compares the model size (in millions of parameters) and the inference time (in seconds) required for 3D reconstruction using different methods. The inference time is likely measured for processing a fixed number of query points in a 3D scene, showcasing the computational efficiency of each approach.

This table presents the breakdown of the computation time required for processing 10,000 points on the ABC dataset using a single NVIDIA 4090 GPU. It shows the time taken by each stage of the proposed PEIF model: SVD (Singular Value Decomposition), PE (Point-wise Feature Extraction), SRM (Spatial Relation Module), PFEM (Patch Feature Extraction Module), IPGE (Intrinsic Patch Geometry Extractor), and other operations.

This table presents a comparison of different methods for 3D shape reconstruction on the ShapeNet dataset. It shows the performance of various methods (including the proposed PEIF) on both base classes (used for training) and novel classes (unseen during training). The metrics used to evaluate performance are: Chamfer distance (CD), Earth Mover’s distance (EMD), Normal Consistency (NC), and F-Score. Lower CD and EMD, and higher NC and F-Score indicate better performance. The table highlights the superior performance of the proposed PEIF, especially its ability to generalize to novel classes.

This table presents the results of the 3D object reconstruction on the ABC dataset using different numbers of input points (5k and 2k). The performance of several methods, including NVF, GeoUDF, GridFormer, and the proposed PEIF, is compared in terms of Chamfer Distance (CD), Earth Mover’s Distance (EMD), Normal Consistency (NC), and F-Score metrics. The table shows how the performance of the methods changes as the number of input points decreases, demonstrating the robustness of PEIF to sparser data.
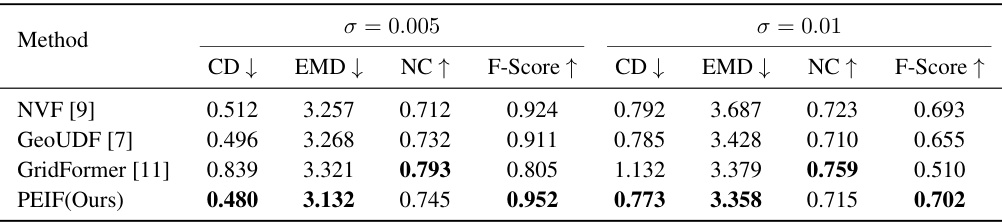
This table presents the results of the 3D object reconstruction experiment conducted on the ABC dataset with added Gaussian noise. The experiment evaluated the performance of several methods (NVF, GeoUDF, GridFormer, and PEIF) under two noise levels (standard deviation σ = 0.005 and σ = 0.01). The metrics used for evaluation include Chamfer distance (CD), Earth Mover’s distance (EMD), Normal Consistency (NC), and F-Score. The table shows that the PEIF method is relatively robust to noise, exhibiting better performance compared to other methods, particularly at higher noise levels.

This table presents a comparison of different methods for 3D shape reconstruction on the ShapeNet dataset. The models are trained on a set of ‘base’ classes and then tested on both the base classes (to measure performance) and ’novel’ classes (to measure generalization ability). The metrics used include Chamfer Distance (CD), Earth Mover’s Distance (EMD), Normal Consistency (NC), and F-Score. Lower CD and EMD indicate better reconstruction accuracy, while higher NC and F-Score signify better performance. The table highlights the performance of PEIF (the proposed method) compared to existing approaches, especially in terms of its generalization ability to novel classes.
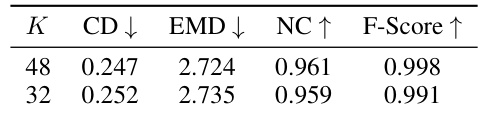
This table presents the ablation study results on the MGN dataset using different numbers of neighbor points (K) during training. The model was trained on the Synthetic Rooms dataset and tested on the MGN dataset. The table shows that the performance is relatively stable across different values of K.
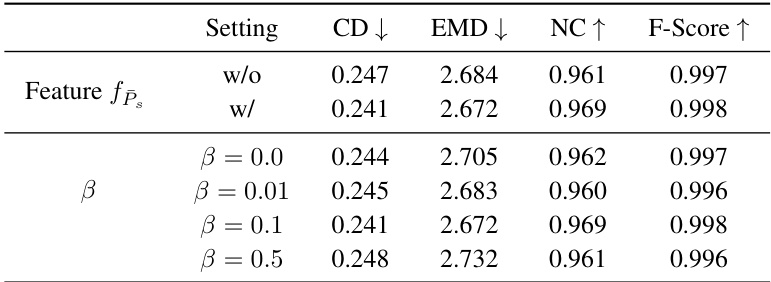
This table presents the results of ablation studies conducted on the ABC dataset to evaluate the impact of different components of the proposed PEIF model. Specifically, it shows the effect of removing pose normalization, the effect of varying the number of heads in the multi-head memory bank, and the effect of using different numbers of nearest neighbors (KNN) for patch selection. The results are evaluated using Chamfer distance (CD), Earth Mover’s Distance (EMD), Normal Consistency (NC), and F-Score metrics.
Full paper#