TL;DR#
Current learned image compression methods heavily rely on hand-crafted causal contexts, limiting their effectiveness. This paper tackles this issue by introducing a novel Causal Context Adjustment loss (CCA-loss). This loss function allows the neural network to learn and adjust the causal context, leading to a more effective autoregressive entropy model and consequently improved compression performance. The problem is exacerbated by the computational burden of existing transformer based methods.
To address these issues, this paper proposes a convolutional neural network (CNN)-based approach with an unevenly channel-wise grouped strategy for high efficiency, reducing the computational cost. Experimental results demonstrate that the proposed method outperforms existing state-of-the-art techniques in terms of rate-distortion performance and compression latency, achieving a significant improvement.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel Causal Context Adjustment loss (CCA-loss) for learned image compression, achieving a great trade-off between inference latency and rate-distortion performance. It also proposes a CNN-based LIC network and an unevenly channel-wise grouped strategy, addressing computational limitations of transformer-based approaches. This opens avenues for improved efficiency and performance in image compression, impacting various applications requiring efficient image storage and transmission.
Visual Insights#
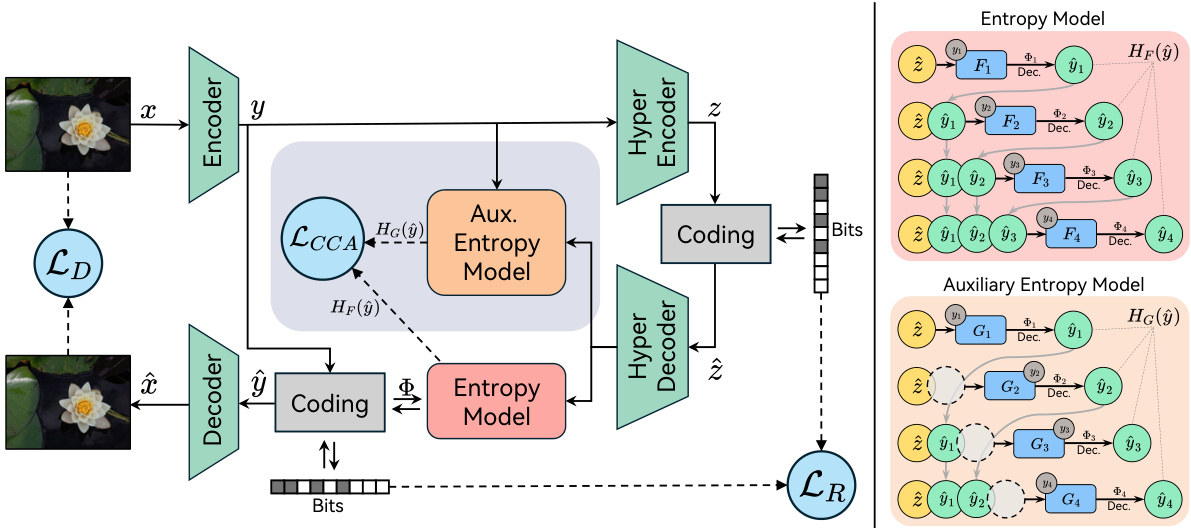
🔼 This figure provides a high-level overview of the proposed method for learned image compression. The left side shows the overall architecture, highlighting the use of a VAE-based framework with a hyperprior and channel-wise autoregressive entropy model. Key components include an encoder, decoder, hyper encoder, hyper decoder, and two entropy models (main and auxiliary). The main contribution, the Causal Context Adjustment loss (LCCA), is also highlighted. The right side illustrates the main and auxiliary entropy models in more detail, emphasizing how the LCCA aims to improve the prediction accuracy by leveraging causal context.
read the caption
Figure 1: Left: A systematic overview of our method. We adopt the VAE-based framework [3] with hyperprior [4] and channel-wise autoregressive entropy model [35]; besides the original Rate-Distortion loss (LR, LD), we introduce an auxiliary entropy model and propose the causal context adjustment loss (LCCA) for better training the entropy model. Right: An illustration of the entropy model and the auxiliary entropy model. The auxiliary entropy model does not use the information to be encoded to predict the following representations, our LCCA encourage the predicting gap between the two models, so as to enhance the importance of causal context in early stages.
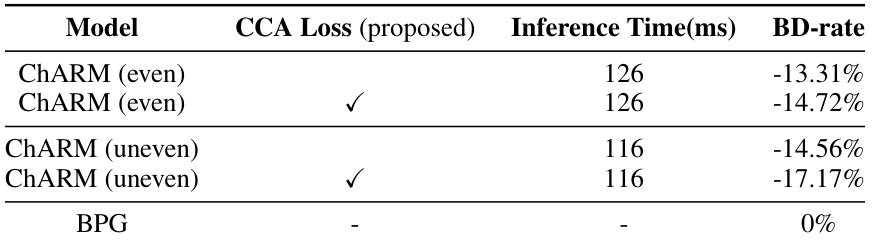
🔼 This table presents the ablation study results on the Kodak dataset. It compares the performance of different autoregressive models with and without the proposed Causal Context Adjustment (CCA) loss. The models are categorized by whether they use an even or uneven channel-wise grouping strategy. The inference time (in milliseconds) and BD-rate (relative to BPG) are reported for each model, showing the effectiveness of CCA loss in improving compression performance.
read the caption
Table 1: Experiments on Kodak dataset. The effects of our proposed Causal Context Adjustment loss (CCA-loss) are verified on various channel-wise autoregressive models. Note that the anchor BD-rate is set as the results of BPG evaluated on Kodak dataset (BD-rate = 0%).
In-depth insights#
Causal Context Loss#
The concept of “Causal Context Loss” in image compression involves leveraging previously decoded information (causal context) to improve the prediction of subsequent parts of the image. A smaller causal context loss suggests that the model effectively utilizes this contextual information, leading to more efficient and accurate compression. The core idea is to explicitly train the model to incorporate important information into earlier stages of the decoding process. This allows the model to make better predictions later, reducing the overall loss and improving rate-distortion performance. Existing methods often rely on hand-crafted causal contexts, limiting their adaptability. In contrast, a learned approach to causal context allows the model to dynamically adjust the information flow based on the data, potentially leading to significant improvements in compression efficiency. A key challenge is designing a loss function that effectively guides the learning process, encouraging the model to prioritize information crucial for accurate prediction, while avoiding overfitting or bias. Success here could yield significant improvements in image compression, reducing both the bitrate and computation time.
CNN Compression#
CNN compression leverages the strengths of Convolutional Neural Networks (CNNs) for efficient image and video compression. CNNs excel at feature extraction and pattern recognition, making them suitable for representing image data in a more compact form. Unlike traditional methods relying on hand-crafted transforms, CNN-based compression learns optimal representations directly from data, potentially achieving higher compression ratios with less distortion. The learning process is crucial, where a CNN is trained to encode and decode data, minimizing the reconstruction error while simultaneously constraining the bitrate. This often involves a rate-distortion optimization framework. However, challenges remain, including computational complexity during training and inference and potential limitations in generalization to unseen data. Architectural innovations, such as efficient network designs and the incorporation of attention mechanisms, continuously improve CNN compression performance and reduce latency. The choice of loss function, and how the rate and distortion components are balanced, is vital in determining the quality-compression tradeoff. Future research directions include exploring more efficient network architectures, refining the loss functions for improved rate-distortion performance and enhancing generalizability.
Autoregressive Models#
Autoregressive models are a cornerstone of modern learned image compression. They leverage the inherent redundancy in images by predicting future pixel values based on previously decoded ones, enabling efficient encoding. This approach is particularly effective because it allows for conditional probability estimation, which refines predictions based on the already known context. The efficiency stems from the reduction in entropy due to this contextual dependence, meaning fewer bits are needed to represent the image. However, a critical challenge is the design of the causal context mechanism, which defines how past information is utilized for prediction. Handcrafted causal context models like those based on channel-wise, checkerboard, or space-channel patterns exist, yet they lack the adaptability to handle diverse image characteristics. Therefore, innovative approaches such as introducing a Causal Context Adjustment Loss to explicitly optimize context formation within the autoregressive framework, offer promise to improve prediction accuracy and compression ratios. This flexibility allows for more optimal representation learning in various image contexts and potentially mitigates limitations of fixed causal context designs.
Uneven Grouping#
The concept of “Uneven Grouping” in the context of learned image compression centers on optimizing the allocation of computational resources and representation capacity across different stages of an autoregressive entropy model. Instead of evenly dividing the channels (features) across stages, an uneven distribution prioritizes more capacity for the initial stages, leveraging the fact that information is encoded more efficiently at the beginning of the process due to the autoregressive nature. Early stages receive a higher allocation of channels, allowing the model to encode more crucial information, enhancing the predictive capability of later stages. This approach is particularly advantageous when paired with a causal context adjustment loss, as it facilitates the efficient transfer of important information early in the coding process. Reduced computational complexity is also a significant benefit, as fewer calculations are required for later stages that have a lower channel count. However, careful parameter tuning is crucial as the uneven distribution necessitates optimizing the rate-distortion trade-off and the schedule of information transmission. A power schedule may be implemented to control the unevenness, requiring careful analysis to determine the optimal allocation for maximal efficiency and performance.
Future of LIC#
The future of Learned Image Compression (LIC) is bright, with several promising avenues for improvement. Efficiency gains are crucial, particularly for high-resolution images and real-time applications. This likely involves exploring novel architectures beyond transformers and CNNs, perhaps incorporating more efficient operations or specialized hardware. Context modeling remains a significant challenge. Developing better methods for representing and utilizing both spatial and temporal context will be key to further enhancing compression ratios. Improved entropy models are also crucial. This could mean finding more accurate probabilistic models or leveraging advancements in information theory. Addressing the trade-off between compression ratio and perceptual quality is a constant challenge. This might entail better integration with human visual perception models to optimize for specific image content and viewing conditions. Furthermore, research into entirely new compression paradigms that go beyond the current VAE-based framework could revolutionize LIC. Finally, tackling the growing demand for efficient compression of various data types beyond images, such as video and 3D models, will be essential for broader adoption of LIC technology.
More visual insights#
More on figures

🔼 This figure provides a high-level overview of the proposed method for learned image compression. The left side shows the overall architecture, highlighting the use of a VAE-based framework with hyperprior and channel-wise autoregressive entropy model. It also emphasizes the introduction of an auxiliary entropy model and a novel Causal Context Adjustment loss (LCCA) to improve training. The right side details the entropy model and auxiliary entropy model, illustrating how LCCA encourages a prediction gap between them to strengthen the importance of causal context in the early stages.
read the caption
Figure 1: Left: A systematic overview of our method. We adopt the VAE-based framework [3] with hyperprior [4] and channel-wise autoregressive entropy model [35]; besides the original Rate-Distortion loss (LR, LD), we introduce an auxiliary entropy model and propose the causal context adjustment loss (LCCA) for better training the entropy model. Right: An illustration of the entropy model and the auxiliary entropy model. The auxiliary entropy model does not use the information to be encoded to predict the following representations, our LCCA encourage the predicting gap between the two models, so as to enhance the importance of causal context in early stages.

🔼 This figure shows the rate-distortion performance curves of the proposed method and other state-of-the-art methods on three different datasets: Kodak, CLIC Professional Validation, and Tecnick. The x-axis represents bits per pixel (bpp), a measure of compression rate, while the y-axis represents PSNR (Peak Signal-to-Noise Ratio), a measure of image quality. The curves illustrate the trade-off between compression and image quality for each method.
read the caption
Figure 3: Rate-Distortion performance evaluation of PSNR on Kodak dataset (left), CLIC Professional Validation dataset (middle), Tecnick dataset (right), respectively.

🔼 This figure shows the rate-distortion performance curves for PSNR on three different datasets: Kodak, CLIC Professional Validation, and Tecnick. The x-axis represents bits per pixel (bpp), indicating the compression rate, and the y-axis represents the peak signal-to-noise ratio (PSNR), measuring image quality. Each line on the graph represents the performance of a different compression method (including the authors’ proposed method and other state-of-the-art methods). This visualization allows for a comparison of the trade-off between compression rate and image quality across various methods and datasets.
read the caption
Figure 3: Rate-Distortion performance evaluation of PSNR on Kodak dataset (left), CLIC Professional Validation dataset (middle), Tecnick dataset (right), respectively.
🔼 The figure illustrates the proposed method for learned image compression. The left side shows a block diagram of the overall system, highlighting the VAE framework with hyperprior, channel-wise autoregressive entropy model, rate-distortion loss, auxiliary entropy model, and the novel causal context adjustment loss (LCCA). The right side provides a detailed view of the entropy and auxiliary entropy models, emphasizing how the LCCA encourages a prediction gap between them to improve the utilization of causal context.
read the caption
Figure 1: Left: A systematic overview of our method. We adopt the VAE-based framework [3] with hyperprior [4] and channel-wise autoregressive entropy model [35]; besides the original Rate-Distortion loss (LR, LD), we introduce an auxiliary entropy model and propose the causal context adjustment loss (LCCA) for better training the entropy model. Right: An illustration of the entropy model and the auxiliary entropy model. The auxiliary entropy model does not use the information to be encoded to predict the following representations, our LCCA encourage the predicting gap between the two models, so as to enhance the importance of causal context in early stages.

🔼 The figure shows the rate-distortion curves for different values of hyperparameter k in the unevenly grouped autoregressive entropy model. The x-axis represents the bits per pixel (bpp), while the y-axis represents the peak signal-to-noise ratio (PSNR). The plot helps to determine the optimal value of k which balances compression efficiency and image quality. The inset plot magnifies the region of interest for better readability.
read the caption
Figure 6: Compression results with different grouped schedules. Detailed experimental settings can be found in the main text.
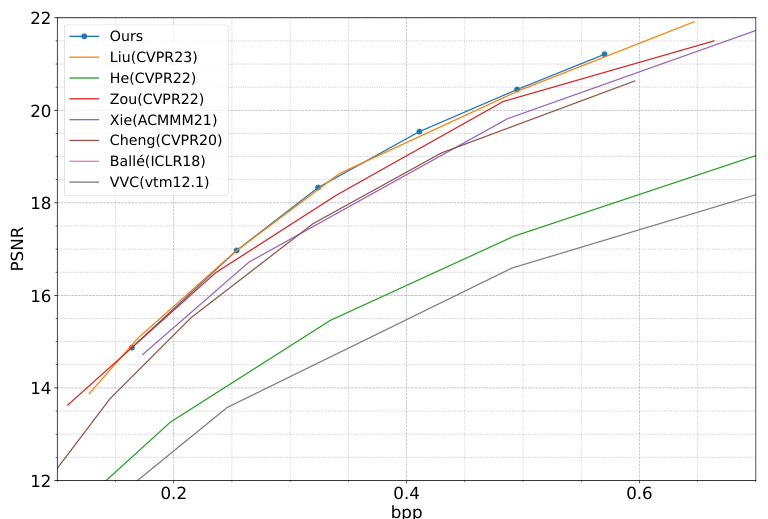
🔼 This figure showcases the rate-distortion performance of the proposed model and compares it to several other state-of-the-art methods and hand-crafted codecs. The plots show the peak signal-to-noise ratio (PSNR) versus bits per pixel (bpp) on three different datasets: Kodak, CLIC Professional Validation, and Tecnick. Each dataset is shown in a separate sub-figure, allowing for a comparison across datasets.
read the caption
Figure 3: Rate-Distortion performance evaluation of PSNR on Kodak dataset (left), CLIC Professional Validation dataset (middle), Tecnick dataset (right), respectively.

🔼 This figure compares the reconstruction results of different image compression methods on the kodim20 image. The methods compared include the authors’ proposed method, VTM (a video compression standard), Liu et al.’s method (a state-of-the-art learned image compression method), and JPEG (a widely used image compression standard). The comparison highlights visual differences in the reconstructed images, particularly in areas of detail such as the propeller and the plane’s markings. The caption includes the bpp (bits per pixel) and PSNR (peak signal-to-noise ratio) values for each method.
read the caption
Figure 8: Visual comparison on reconstructed propeller airplane (kodim20) image.

🔼 This figure compares the visual quality of reconstructed images of the kodim24 image using different methods: Ground Truth (original image), VTM (Versatile Video Coding), Liu et al. (a state-of-the-art learned image compression method), WebP (a lossy image compression format), and the proposed method in this paper (Ours). The image shows the details of the reconstruction, especially focusing on intricate patterns on a wall of a house. The metrics [bpp | PSNR(dB)] shown below each image indicate bits per pixel and Peak Signal-to-Noise Ratio values, respectively, which are commonly used to evaluate the trade-off between compression ratio and image quality. The results highlight the better preservation of visual details in the proposed method.
read the caption
Figure 9: Visual comparison on reconstructed pattern on the walls of the house (kodim24) image.
More on tables
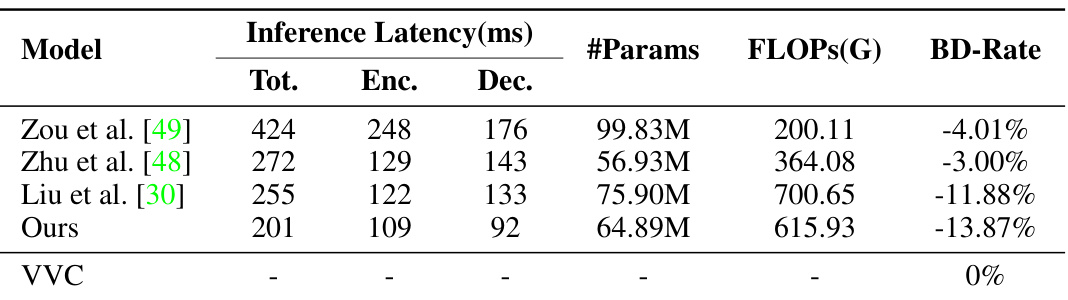
🔼 This table compares different learned image compression models’ coding complexity. It includes the total, encoding, and decoding inference latency in milliseconds, the number of parameters in millions, the number of floating-point operations (FLOPs) in billions, and the BD-rate (percentage improvement over VVC). Lower BD-rate indicates better compression performance.
read the caption
Table 2: Comparison of coding complexity evaluated on Kodak dataset. All the models are evaluated on the same platform. The lower BD-rate is better.
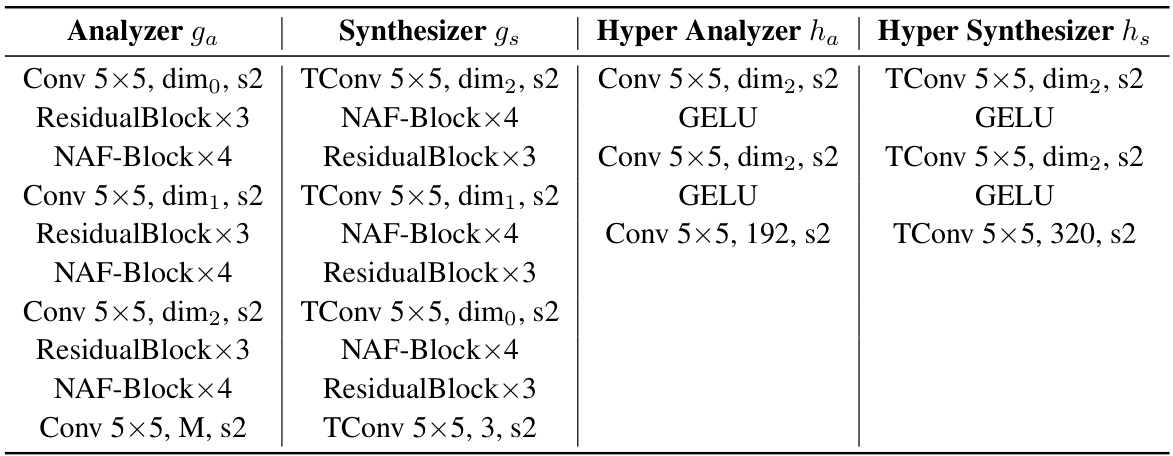
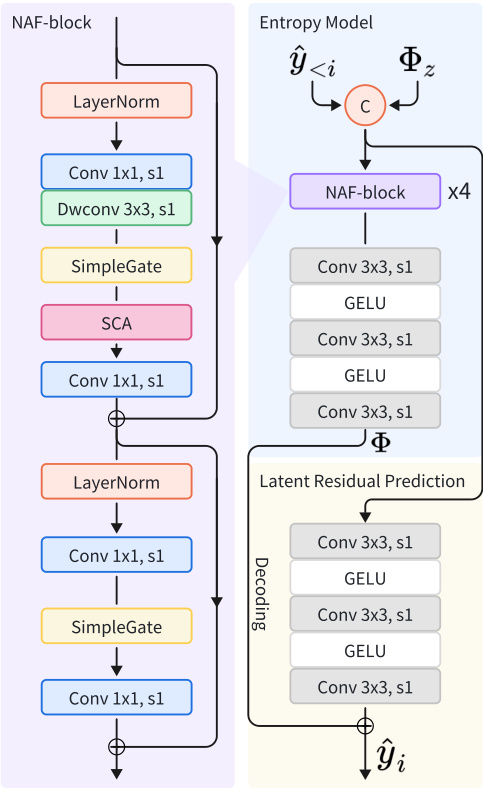
🔼 This table details the architecture of the main transforms (analyzer and synthesizer) and hyper transforms (hyper analyzer and hyper synthesizer) used in the paper’s image compression framework. It lists the convolutional layers (Conv), transposed convolutional layers (TConv), residual blocks (ResidualBlock), NAF blocks (NAF-Block), and GELU activation functions used in each part of the network. The ‘dim’ parameters represent the number of channels used in different parts of the network, and ‘s2’ indicates a stride of 2 for downsampling/upsampling operations. M represents the number of input channels (3 for RGB images).
read the caption
Table 3: Architecture of main transforms and hyper transforms.
Full paper#



















