↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world datasets contain significant noise, which can hinder the development of simple and interpretable machine learning models. This is problematic as simpler models are easier to understand and troubleshoot, making them more suitable for high-stakes decision-making. Existing research has shown that noise can lead to simpler models, but hasn’t provided a clear quantitative relationship between noise levels and model simplicity. This lack of understanding limits our ability to predict when simple models are likely to exist, which is important for making informed decisions in high-stakes settings.
This paper addresses this gap by investigating the relationship between noise and model simplicity across various hypothesis spaces, focusing on decision trees and linear models. The researchers formally prove that noise acts as an implicit regularizer, leading to simpler models. They also show that Rashomon sets (sets of near-optimal models) built using noisy data tend to contain simpler models than those built from non-noisy data. Further, they demonstrate that noise expands the set of good features, which ultimately increases the likelihood of models utilizing at least one good feature, providing theoretical guarantees and practical insights for using simple and accurate models. These findings provide valuable guidance for data scientists and policymakers in predicting the simplicity of models based on data noise levels.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with noisy data, as it provides theoretical guarantees and practical guidance on how noise impacts model simplicity and the Rashomon effect. It offers new avenues for research in developing robust and interpretable machine learning models, particularly in high-stakes domains.
Visual Insights#
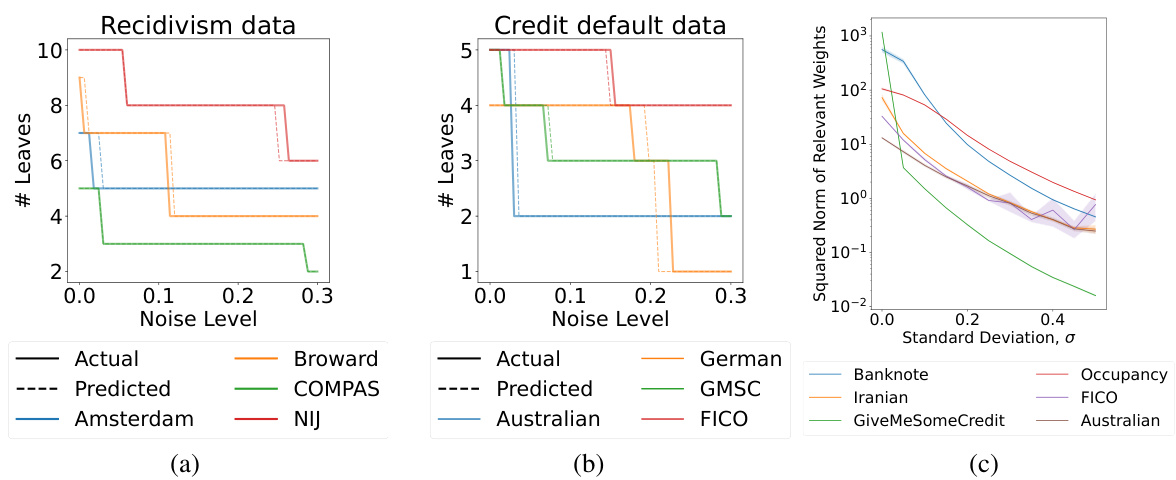
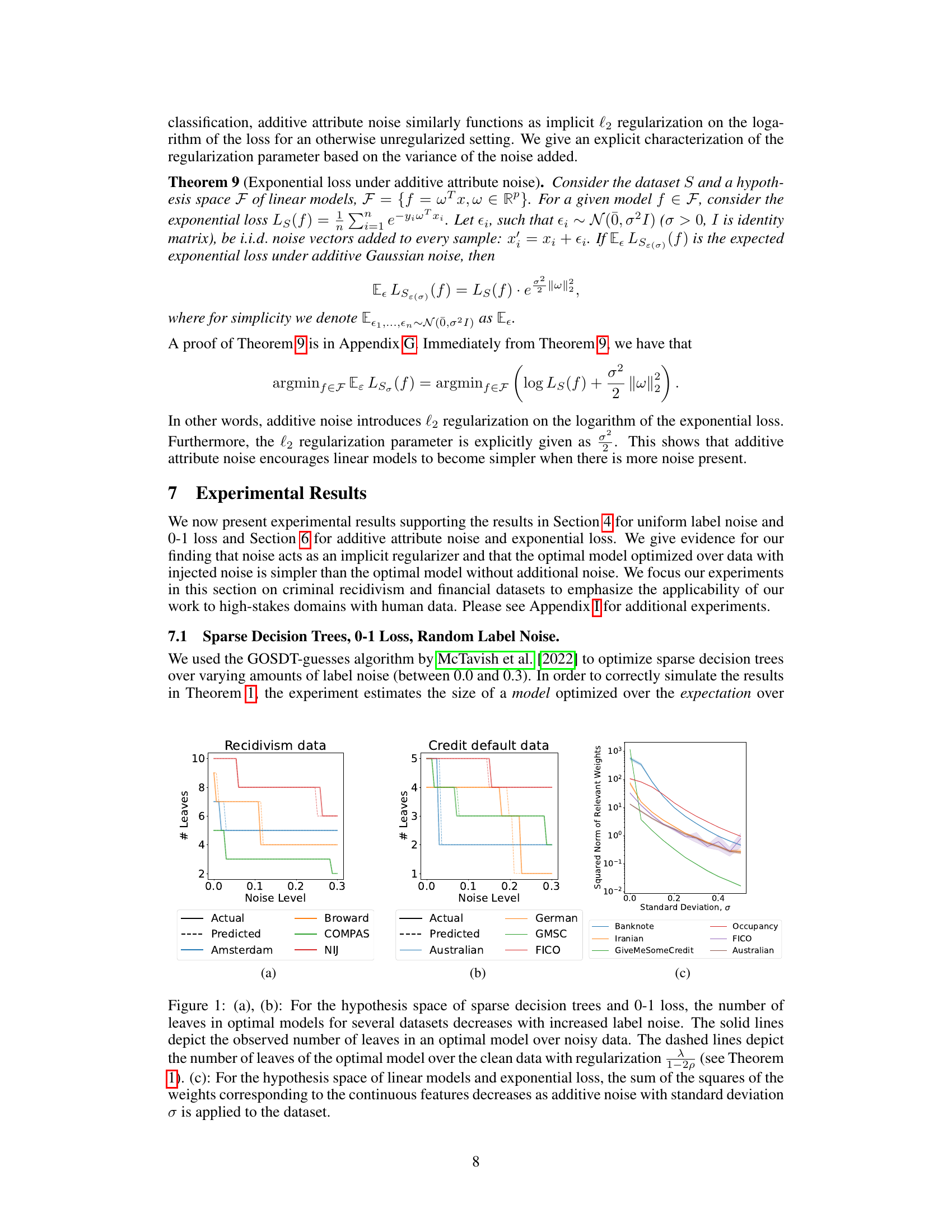
Figure 1 shows the effect of noise (label and additive attribute noise) on model complexity for sparse decision trees and linear models. Subfigures (a) and (b) demonstrate that for sparse decision trees, increasing label noise reduces the optimal model’s number of leaves. This aligns with the theoretical results showing that noise acts as an implicit regularizer. Subfigure (c) illustrates that for linear models using exponential loss, increasing additive attribute noise decreases the squared norm of relevant weights (a measure of model complexity).
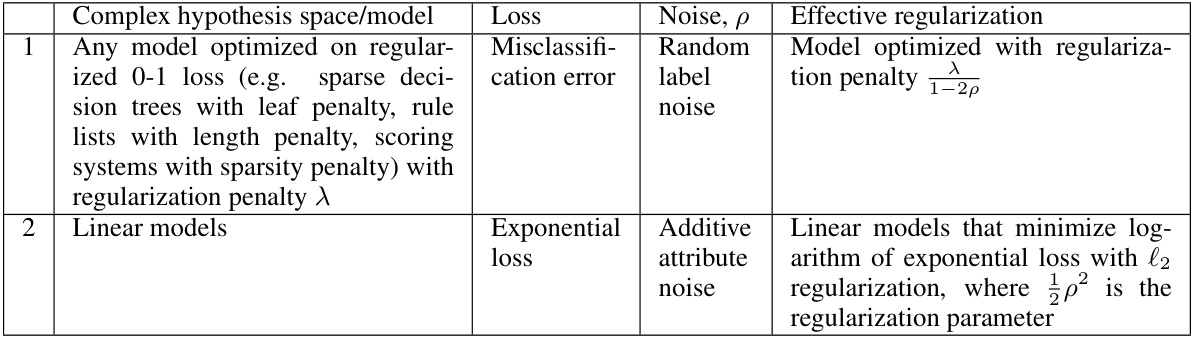
This table summarizes the main contributions of the paper and answers its key research question regarding the relationship between noise levels in data and model simplicity. It shows how different types of noise in various hypothesis spaces (such as sparse decision trees and linear models) affect model complexity and regularization. For each combination of hypothesis space, loss function, and noise type, the table provides the effective regularization that is implicitly added by the presence of noise. This allows for a better understanding of the extent of model simplification that can be expected under different noise levels, offering theoretical guarantees and practical insights for practitioners and policymakers.
In-depth insights#
Noise as Regularizer#
The concept of ‘Noise as Regularizer’ explores how the introduction of noise into a dataset can unexpectedly improve model simplicity and generalization. Noise acts as an implicit regularizer, effectively simplifying the model selection process without explicit regularization techniques. This occurs because noise distorts high-quality features more significantly than low-quality ones, implicitly increasing the regularization strength. This effect is formally proven for several noise models and hypothesis spaces (e.g., decision trees and linear models) demonstrating that models trained on noisy data can be shown to be equivalent to models trained on clean data with stronger regularization. The implications are significant for high-stakes decision-making, suggesting that the presence of noise in real-world data might lead to simpler, interpretable, and possibly more robust models with comparable performance to complex ones. This finding challenges the traditional accuracy-simplicity trade-off often cited in machine learning, suggesting simpler models may be sufficient in noisy contexts. Furthermore, it suggests a potential avenue for controlling model complexity by tuning noise levels, offering new possibilities in algorithm design and policy decisions. The theoretical guarantees presented in the paper are supported by empirical evidence using diverse datasets, adding further weight to the significance of noise as a regularization tool.
Rashomon Simplicity#
The concept of “Rashomon Simplicity” proposes that noise in data can paradoxically lead to simpler yet accurate models. This challenges the traditional trade-off between model complexity and accuracy. The Rashomon effect, where multiple good models exist for a single dataset, is central to this idea. The presence of noise expands the Rashomon set, increasing the likelihood that simpler models are among the top performers. This finding has significant implications for policy and practice, suggesting that in noisy real-world settings, simpler models may be sufficient and preferable due to their interpretability and ease of use, potentially outweighing any small loss in predictive accuracy. Further research could explore the relationship between noise level, model simplicity, and the specific characteristics of the dataset to optimize the balance between simplicity and performance.
Feature Set Growth#
The concept of ‘Feature Set Growth’ within the context of noisy data is a crucial finding. The paper demonstrates that introducing noise increases the number of features considered ‘good’. This is because noise disproportionately affects high-quality features, reducing their signal-to-noise ratio more significantly than lower-quality features. Consequently, the set of features with AUC (Area Under the ROC Curve) values close to the best feature expands. This impacts model simplicity: While regularization might decrease model complexity in the presence of noise, the expanded feature set with more equally
Empirical Datasets#
The effectiveness of the proposed methods is rigorously evaluated using diverse empirical datasets. A key strength lies in the selection of datasets from high-stakes domains, including criminal justice and finance, which directly demonstrates the practical applicability of the research. The inclusion of both real-world and synthetic datasets enhances the generalizability of the findings. The careful pre-processing steps applied to the datasets, such as handling missing values and balancing classes, ensure data quality and reliability. Moreover, the detailed description of data characteristics and preprocessing techniques facilitates reproducibility and allows others to replicate the experiments. Overall, the comprehensive approach to dataset selection and preparation strengthens the credibility and impact of the research, providing strong evidence supporting the theoretical claims.
Future Directions#
Future research could explore extending the theoretical framework to diverse loss functions beyond 0-1 loss and exponential loss, encompassing hinge loss and logistic loss. Investigating the impact of non-uniform noise models, moving beyond the uniform label noise and additive attribute noise, presents a significant opportunity. This includes exploring scenarios with non-uniform noise in labels or inputs, and potentially incorporating noise models that account for dependencies between features or noise patterns within specific domains. Furthermore, developing more refined quantitative relationships between noise levels, model simplicity, and the Rashomon set would provide a deeper understanding of the interplay of these factors. This could involve exploring alternative metrics for assessing model simplicity, as well as studying the behavior of the Rashomon set under different regularization schemes and hypothesis spaces. Finally, extending empirical analysis to a wider range of high-stakes domains, incorporating more sophisticated techniques and datasets, would further validate and strengthen the current findings, providing robust practical guidance for various applications. Specifically, this includes carefully analyzing domains with inherent complexities or biases, evaluating the impact of noise on fairness considerations, and investigating the implications of these findings for policymakers and stakeholders in high-stakes decision-making.
More visual insights#
More on figures
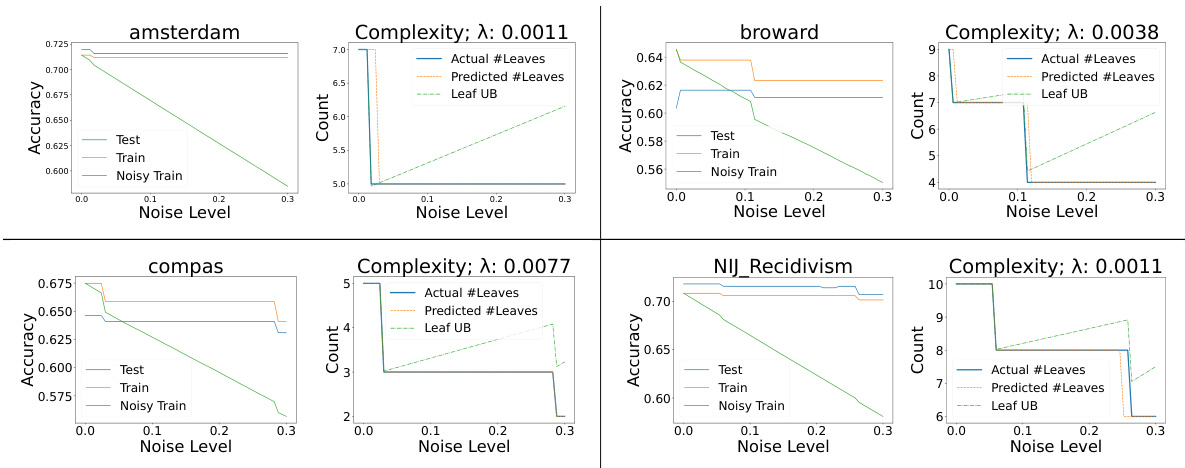
This figure shows the experimental results on recidivism datasets for Section 4 of the paper. The left side shows accuracy plots, while the right side shows complexity plots. The accuracy plots compare the performance of models trained on clean data versus noisy data. The complexity plots compare the number of leaves in optimal models trained under different conditions (noisy data, clean data with regularization). The green line represents an upper bound on the number of leaves calculated using Corollary 10 from the paper. The regularization parameter (lambda) was optimized using 5-fold cross-validation.

This figure shows the impact of noise on the complexity of models within the Rashomon set, which is a set of near-optimal models. The left panel (a) aggregates results over 23 datasets (both synthetic and real-world) while the right panel (b) focuses specifically on 9 real-world recidivism and finance datasets. For each noise level (0%, 10%, 20%, 30%), the number of leaves (model complexity) in the models of the Rashomon set is visualized using a bar chart. The figure empirically shows that as the noise level increases, the distribution of the number of leaves shifts towards lower values, indicating simpler models within the Rashomon set.
This figure shows the effect of label noise and additive attribute noise on model complexity for sparse decision trees and linear models, respectively. The left and center plots demonstrate that the number of leaves in optimal decision trees decreases as label noise increases, aligning with theoretical predictions. The right plot illustrates that the sum of squared weights in linear models decreases with increased additive attribute noise, also supporting the paper’s theoretical claims about noise acting as an implicit regularizer.

This figure shows the distribution of Area Under the ROC Curve (AUC) values for features in a set of datasets before and after adding 15% label noise. The left panel shows the distribution for clean labels, while the right shows the distribution after adding noise. The key observation is that, with the addition of noise, high-AUC features (those that strongly correlate with the labels) lose signal more quickly than low-AUC features. This effect is visualized by the shift in the distribution to the left and the widening of the green shaded area, which represents the set of features within a certain AUC threshold of the best feature. The expansion of this set demonstrates that the addition of noise increases the number of features that are relatively useful for prediction.
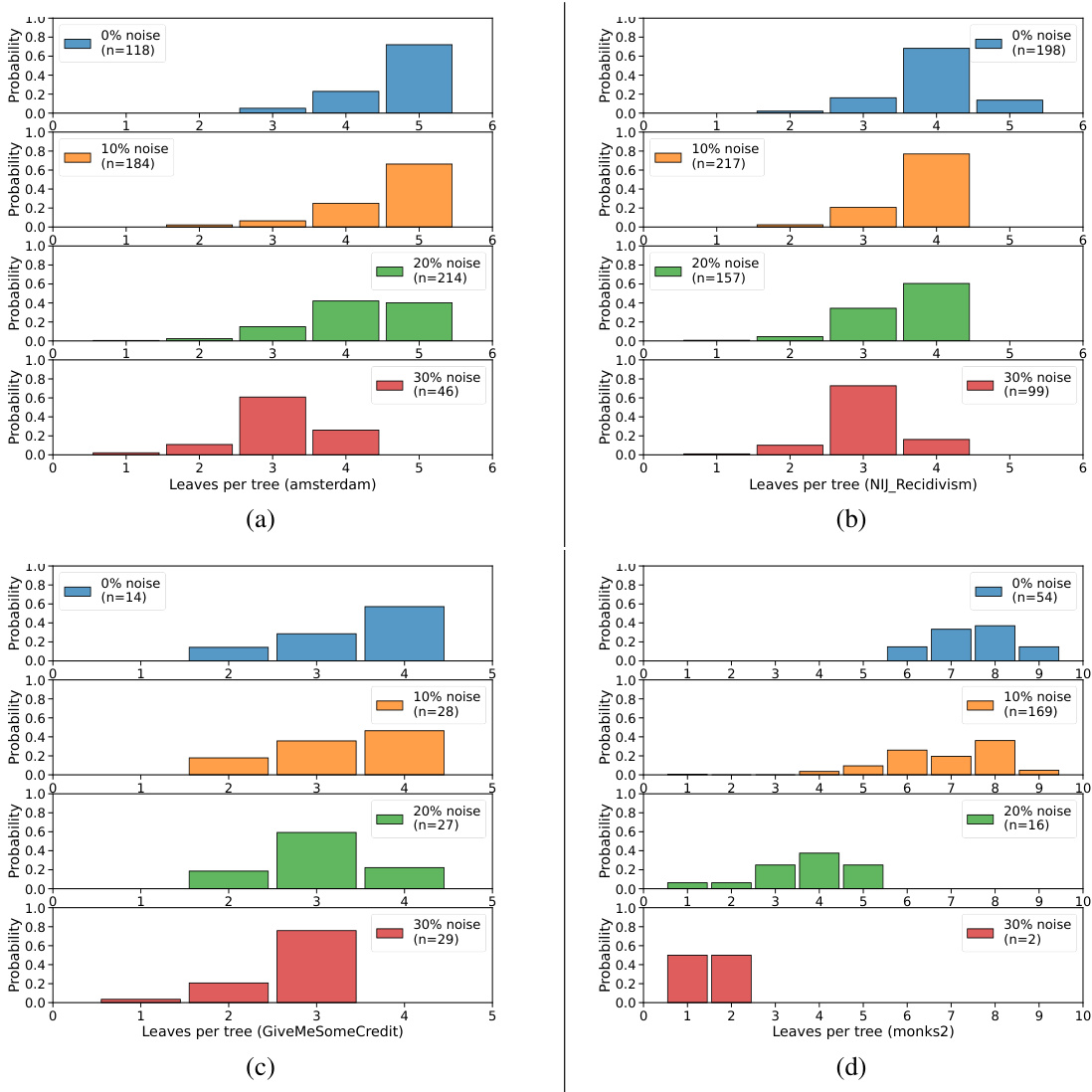
This figure shows the effect of noise on the complexity of models within the Rashomon set (a set of near-optimal models). The bar charts display the distribution of the number of leaves (a measure of model complexity) in decision trees for different noise levels. Panel (a) aggregates results across 23 diverse datasets, while panel (b) focuses specifically on 9 real-world recidivism and finance datasets. The results demonstrate that as noise increases, the models within the Rashomon set tend to become simpler (fewer leaves).
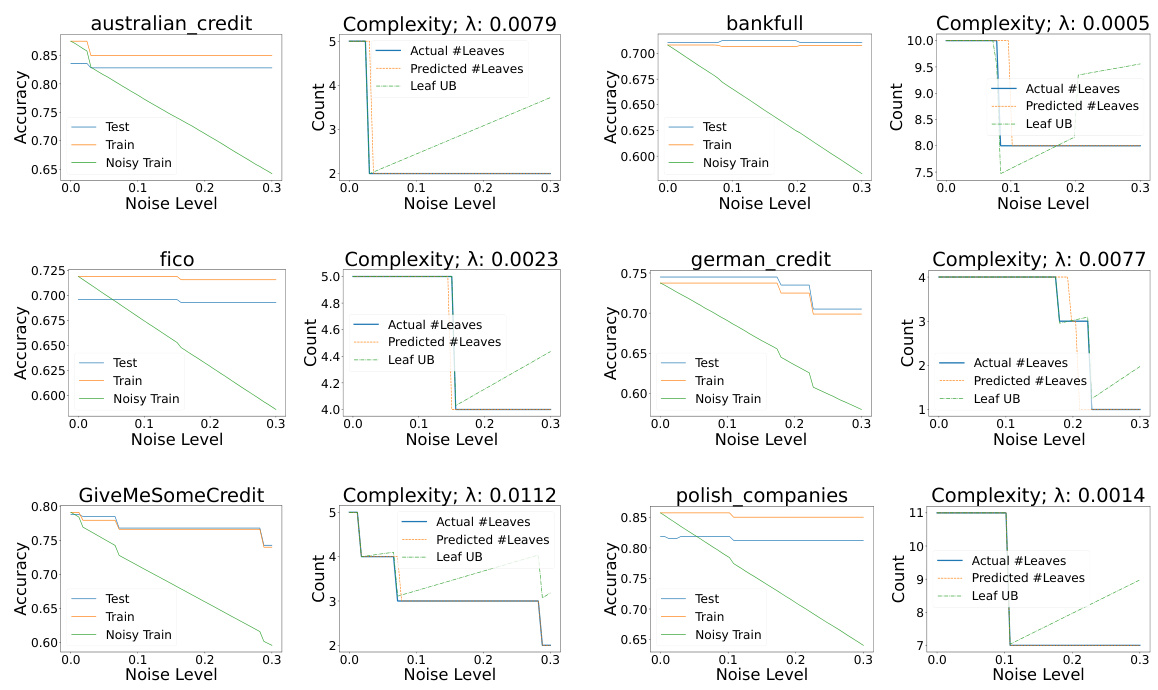
This figure shows experimental results for Section 4 (Random Label Noise and Regularized 0-1 Loss) applied to financial datasets. For each dataset, it displays plots showing the accuracy (test, train, and noisy train) and model complexity (’leaves’ in a decision tree) across different levels of label noise. The dashed lines represent predictions of the number of leaves based on theoretical results, demonstrating an alignment between theory and experiment in how noise affects model complexity. The Appendix I.2 provides details on the experimental design.

Figure 1 presents experimental results that support the theoretical findings of the paper. The plots show how model complexity (number of leaves for decision trees, sum of squared weights for linear models) changes with increasing label noise or additive attribute noise, for several different datasets. The results confirm that noise acts as an implicit regularizer, leading to simpler models.
More on tables
This table summarizes the main theoretical results of the paper. For various combinations of hypothesis spaces (complex models optimized on regularized 0-1 loss, linear models), loss functions (0-1 loss, exponential loss), and noise types (random label noise, additive attribute noise), the table shows how the addition of noise acts as an implicit regularizer, making the optimization problem equivalent to optimizing the clean data with stronger regularization. The table provides a concise overview of the main theoretical contributions which are later supported empirically.

This table summarizes the main findings of the paper by showing how different types of noise affect model simplicity for various combinations of hypothesis spaces and loss functions. For each scenario, it indicates the type of noise added, the resulting effective regularization, and the corresponding simplified model.
Full paper#